oneapi::mkl::rng::binomial¶

Generates binomially distributed random numbers.

Description ¶

The oneapi::mkl::rng::binomial class object is used in the oneapi::mkl::rng::generate function to provide binomially distributed random numbers with number of independent Bernoulli trials m, and with probability p of a single trial success, where p∈R; 0 ≤p≤ 1, m∈N.

A binomially distributed variate represents the number of successes in m independent Bernoulli trials with probability of a single trial success p.

The probability distribution is given by:

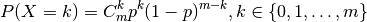
$P(X = k) = C_m^k p^k (1-p)^{m-k}, k \in \{0, 1, \ldots, m\}$

The cumulative distribution function is as follows:

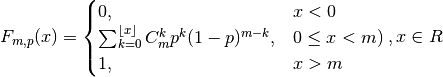
$F_{m, p} (x) = \begin{cases} 0, & x < 0 \\ \sum_{k = 0}^{\lfloor x \rfloor} C_m^k p^k (1-p)^{m-k}, & 0 \leq x < m)\\ 1, & x > m \end{cases}, x \in R$

Product and Performance Information
Performance varies by use, configuration and other factors. Learn more at https://www.intel.com/PerformanceIndex. Notice revision #20201201

API ¶

Syntax¶

template<typename IntType = std::int32_t,
  typename Method = binomial_method::by_default>
  class binomial {
  public:
  using method_type = Method;
  using result_type = IntType;
  binomial(): binomial(5, 0.5){}
  explicit binomial(std::int32_t ntrial, double p);
  explicit binomial(const param_type& pt);
  std::int32_t ntrial() const;
  double p() const;
  param_type param() const;
  void param(const param_type& pt);
};

Devices supported: Host, CPU, and GPU.

Include Files¶

oneapi/mkl/rng.hpp

Template Parameters¶

Name	Description
`typename IntType = std::int32_t`	Type of the produced values. The specific values are as follows: `std::int32_t` `std::uint32_t`
`typename Method = oneapi::mkl::rng:: binomial_method:: by_default`	Generation method. The specific values are as follows: `oneapi::mkl::rng::binomial_method::btpe` See brief descriptions of the methods in Distributions Template Parameter Method.

Name

Description

typename IntType = std::int32_t

Type of the produced values. The specific values are as follows:

std::int32_t

std::uint32_t

typename Method = oneapi::mkl::rng:: binomial_method:: by_default

Generation method. The specific values are as follows:

oneapi::mkl::rng::binomial_method::btpe

See brief descriptions of the methods in Distributions Template Parameter Method.

Input Parameters¶

Name	Type	Description
ntrials	`std::int32_t`	Number of independent trials.
p	`double`	Success probability `p` of a single trial.

oneapi::mkl::rng::geometric oneapi::mkl::rng::hypergeometric

oneAPI Math Kernel Library (oneMKL) documentation