gebrd (USM Version)¶

Reduces a general matrix to bidiagonal form. This routine belongs to the oneapi::mkl::lapack namespace.

Description ¶

The routine reduces a general m-by-n matrix A to a bidiagonal matrix B by an orthogonal (unitary) transformation.

If m≥n, the reduction is given by

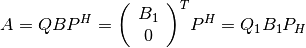
$A = QBP^H = {\left( \begin{array}{ccc} B_1 \\ 0 \end{array} \right)}^T P^H = Q_1 B_1 P_H$

where B₁ is an n-by-n upper diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; Q₁ consists of the first n columns of Q.

If m < n, the reduction is given by

A = Q*B*PH = Q*(B10)*PH = Q1*B1*P1H,

where B₁ is an m-by-m lower diagonal matrix, Q and P are orthogonal or, for a complex A, unitary matrices; P₁ consists of the first m columns of P.

The routine does not form the matrices Q and P explicitly, but represents them as products of elementary reflectors. Routines are provided to work with the matrices Q and P in this representation:

If the matrix A is real,

to compute Q and P explicitly, call orgbr (USM Version).

If the matrix A is complex,

to compute Q and P explicitly, call ungbr (USM Version).

API ¶

Syntax¶

namespace oneapi::mkl::lapack {
  cl::sycl::event gebrd(cl::sycl::queue &queue,
            std::int64_t m,
            std::int64_t n,
            T *a,
            std::int64_t lda,
            RealT *d,
            RealT *e,
            T *tauq,
            T *taup,
            T *scratchpad,
            std::int64_t scratchpad_size, const std::vector<cl::sycl::event> &events = {})
}

gebrd (USM version) supports the following precisions and devices:

T	Devices supported
`float`	Host, CPU, GPU
`double`	Host, CPU, GPU
`std::complex<float>`	Host, CPU, GPU
`std::complex<double>`	Host, CPU, GPU

Input Parameters¶

queue: Device queue where calculations will be performed.
m: The number of rows in the matrix A (0≤m).
n: The number of columns in the matrix A (0≤n).
a: Pointer to matrix A. The second dimension of a must be at least max(1, m).
lda: The leading dimension of a.
scratchpad: Pointer to scratchpad memory to be used by the routine for storing intermediate results.
scratchpad_size: Size of scratchpad memory as a number of floating point elements of type T. Size should not be less than the value returned by the gebrd_scratchpad_size function.
events: List of events to wait for before starting computation. Defaults to empty list.

Output Parameters¶

a

If m≥n, the diagonal and first super-diagonal of a are overwritten by the upper bidiagonal matrix B. The elements below the diagonal, with the tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the first superdiagonal, with the taup, represent the orthogonal matrix P as a product of elementary reflectors.

If m<n, the diagonal and first sub-diagonal of a are overwritten by the lower bidiagonal matrix B. The elements below the first subdiagonal, with the tauq, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the diagonal, with the taup, represent the orthogonal matrix P as a product of elementary reflectors.

d

Pointer to memory of size at least max(1, min(m,n)). Contains the diagonal elements of B.

e

Pointer to memory of size at least max(1, min(m,n) - 1). Contains the off-diagonal elements of B.

tauq

Pointer to memory of size at least max(1, min(m, n)). The scalar factors of the elementary reflectors which represent the orthogonal or unitary matrix Q.

taup

Pointer to memory of size at least max(1, min(m, n)). The scalar factors of the elementary reflectors which represent the orthogonal or unitary matrix P.

Exceptions¶

Exception	Description
`mkl::lapack::exception`	This exception is thrown when problems occur during calculations. You can obtain the info code of the problem using the info() method of the exception object: If `info = -i`, the `i`-th parameter had an illegal value. If `info` is equal to the value passed as scratchpad size, and detail() returns non zero, then the passed scratchpad has an insufficient size, and the required size should not be less than the value returned by the detail() method of the exception object.

Exception

Description

mkl::lapack::exception

This exception is thrown when problems occur during calculations. You can obtain the info code of the problem using the info() method of the exception object:

If info = -i, the i-th parameter had an illegal value.

If info is equal to the value passed as scratchpad size, and detail() returns non zero, then the passed scratchpad has an insufficient size, and the required size should not be less than the value returned by the detail() method of the exception object.

Return Values¶

Output event to wait on to ensure computation is complete.

gebrd gebrd_scratchpad_size

oneAPI Math Kernel Library (oneMKL) documentation