Contents

hemv

Computes a matrix-vector product using a hermitian matrix.

Description

The hemv routines compute a scalar-matrix-vector product and add the result to a scalar-vector product, with a hermitian matrix. The operation is defined as:

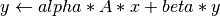
y \leftarrow alpha*A*x + beta*y

where:

  • alpha and beta are scalars

  • A is n x n hermitian matrix

  • x and y are vectors of length n

hemv supports the following precisions:

T

std::complex<float>

std::complex<double>

hemv (Buffer Version)

Syntax

namespace oneapi::mkl::blas::column_major {
    void hemv(sycl::queue &queue,
              oneapi::mkl::uplo upper_lower,
              std::int64_t n,
              T alpha,
              sycl::buffer<T,1> &a,
              std::int64_t lda,
              sycl::buffer<T,1> &x,
              std::int64_t incx,
              T beta,
              sycl::buffer<T,1> &y,
              std::int64_t incy)
}

namespace oneapi::mkl::blas::row_major {
    void hemv(sycl::queue &queue,
              oneapi::mkl::uplo upper_lower,
              std::int64_t n,
              T alpha,
              sycl::buffer<T,1> &a,
              std::int64_t lda,
              sycl::buffer<T,1> &x,
              std::int64_t incx,
              T beta,
              sycl::buffer<T,1> &y,
              std::int64_t incy)
}

Input Parameters

queue

The queue where the routine should be executed.

upper_lower

Specifies whether matrix A is upper or lower triangular. See Data Types for more details.

n

Number of rows and columns of matrix A. Must be at least zero.

alpha

Scaling factor for the matrix-vector product.

a

Buffer holding input matrix A. Size of the buffer must be at least lda * n. See Matrix Storage for more details.

lda

Leading dimension of matrix A. Must be at least n and positive.

x

Buffer holding input vector x. Size of the buffer must be at least (1 + (n - 1)*abs(incx)). See Matrix Storage for more details.

incx

Stride of vector x.

beta

Scaling factor for vector y.

y

Buffer holding input/output vector y. Size of the buffer must be at least (1 + (n - 1)*abs(incy)). See Matrix Storage for more details.

incy

Stride of vector y.

Output Parameters

y

Buffer holding updated vector y.

hemv (USM Version)

Syntax

namespace oneapi::mkl::blas::column_major {
    sycl::event hemv(sycl::queue &queue,
                     oneapi::mkl::uplo upper_lower,
                     std::int64_t n,
                     T alpha,
                     const T *a,
                     std::int64_t lda,
                     const T *x,
                     std::int64_t incx,
                     T beta,
                     T *y,
                     std::int64_t incy,
                     const std::vector<sycl::event> &dependencies = {})
}

namespace oneapi::mkl::blas::row_major {
    sycl::event hemv(sycl::queue &queue,
                     oneapi::mkl::uplo upper_lower,
                     std::int64_t n,
                     T alpha,
                     const T *a,
                     std::int64_t lda,
                     const T *x,
                     std::int64_t incx,
                     T beta,
                     T *y,
                     std::int64_t incy,
                     const std::vector<sycl::event> &dependencies = {})
}

Input Parameters

queue

The queue where the routine should be executed.

upper_lower

Specifies whether matrix A is upper or lower triangular. See Data Types for more details.

n

Number of rows and columns of matrix A. Must be at least zero.

alpha

Scaling factor for the matrix-vector product.

a

Pointer to input matrix A. Size of the array holding input matrix A must be at least lda * n. See Matrix Storage for more details.

lda

Leading dimension of matrix A. Must be at least n and positive.

x

Pointer to input vector x. Size of the array holding input vector x must be at least (1 + (n - 1)*abs(incx)). See Matrix Storage for more details.

incx

Stride of vector x.

beta

Scaling factor for vector y.

y

Pointer to input/output vector y. Size of the array holding input/output vector y must be at least (1 + (n - 1)*abs(incy)). See Matrix Storage for more details.

incy

Stride of vector y.

dependencies

List of events to wait for before starting computation, if any. If omitted, defaults to no dependencies.

Output Parameters

y

Pointer to updated vector y.

Return Values

Output event to wait on to ensure computation is complete.

hbmv her