Contents

Cubic Splines

Cubic splines are splines whose degree is equal to 3.

Cubic splines are described by the following polynomial

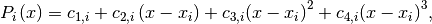
P_i\left( x \right) = c_{1,i}+ c_{2,i}\left( x - x_i \right) + c_{3,i}{\left( x - x_i \right)}^2+ c_{4,i}{\left( x - x_i \right)}^3,

where

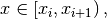
x \in \left[ x_i, x_{i+1} \right),

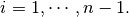
i = 1,\cdots , n-1.

There are a lot of different types of cubic splines: Hermite, natural, Akima, Bessel. However, the current version of DPC++ API supports only one type: Hermite.

Header File

#include<oneapi/mkl/experimental/data_fitting.hpp>

Namespace

oneapi::mkl::experimental::data_fitiing

Hermite Spline

Coefficients of Hermite spline are calculated using the following formulas:

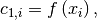
c_{1,i} = f\left( x_i \right),

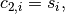
c_{2,i} = s_i,

c_{3,i} = \left( \left[ x_i, x_{i+1} \right]f - s_i \right) / \left( \Delta x_i \right) - c_{4,i}\left( \Delta x_i \right),

c_{4,i} = \left( s_i + s_{i+1} - 2\left[ x_i, x_{i+1} \right]f \right) / {\left( \Delta x_i \right)}^2,

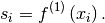
s_i = f^{\left( 1 \right)}\left( x_i \right).

The following boundary conditions are supported for Hermite spline:

  • Free end (f^{(2)}(x_1) = f^{(2)}(x_n) = 0).

  • Periodic.

  • First derivative.

  • Second Derivative.

Syntax

namespace cubic_spline {
  struct hermite {};
}

Example

To create a cubic Hermite spline object use the following:

spline<float, cubic_spline::hermite> val(
  /*SYCL queue object*/q,
  /*number of spline functions*/ny
);

Follow the Examples section to see more complicated examples.

Linear Spline Interpolate Function