gemmt¶

Computes a matrix-matrix product with general matrices, but updates only the upper or lower triangular part of the result matrix.

Description¶

The gemmt routines compute a scalar-matrix-matrix product and add the result to the upper or lower part of a scalar-matrix product, with general matrices. The operation is defined as:

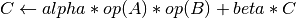
$C \leftarrow alpha*op(A)*op(B) + beta*C$

where:

op(X) is one of op(X) = X, or op(X) = X^T, or op(X) = X^H
alpha and beta are scalars
A, B, and C are matrices
op(A) is n x k, op(B) is k x n, and C is n x n

gemmt supports the following precisions:

T
`float`
`double`
`std::complex<float>`
`std::complex<double>`

gemmt (Buffer Version)¶

Syntax¶

namespace oneapi::mkl::blas::column_major {
    void gemmt(sycl::queue &queue,
               oneapi::mkl::uplo upper_lower,
               oneapi::mkl::transpose transa,
               oneapi::mkl::transpose transb,
               std::int64_t n,
               std::int64_t k,
               T alpha,
               sycl::buffer<T,1> &a,
               std::int64_t lda,
               sycl::buffer<T,1> &b,
               std::int64_t ldb,
               T beta,
               sycl::buffer<T,1> &c,
               std::int64_t ldc)
}

namespace oneapi::mkl::blas::row_major {
    void gemmt(sycl::queue &queue,
               oneapi::mkl::uplo upper_lower,
               oneapi::mkl::transpose transa,
               oneapi::mkl::transpose transb,
               std::int64_t n,
               std::int64_t k,
               T alpha,
               sycl::buffer<T,1> &a,
               std::int64_t lda,
               sycl::buffer<T,1> &b,
               std::int64_t ldb,
               T beta,
               sycl::buffer<T,1> &c,
               std::int64_t ldc)
}

Input Parameters¶

queue

The queue where the routine should be executed.

upper_lower

Specifies whether matrix C is upper or lower triangular. See Data Types for more details.

transa

Specifies op(A), the transposition operation applied to matrix A. See Data Types for more details.

transb

Specifies op(B), the transposition operation applied to matrix B. See Data Types for more details.

n

Number of rows of matrix op(A) and matrix C. Must be at least zero.

k

Number of columns of matrix op(A) and rows of matrix op(B). Must be at least zero.

alpha

Scaling factor for matrix-matrix product.

a

Buffer holding input matrix A. See Matrix Storage for more details.

	`transa` = `transpose::nontrans`	`transa` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	`A` is `n` x `k` matrix. Size of array `a` must be at least `lda` * `k`	`A` is `k` x `n` matrix. Size of array `a` must be at least `lda` * `n`
Row major	`A` is `n` x `k` matrix. Size of array `a` must be at least `lda` * `n`	`A` is `k` x `n` matrix. Size of array `a` must be at least `lda` * `k`

lda

Leading dimension of matrix A. Must be positive.

	`transa` = `transpose::nontrans`	`transa` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	Must be at least `n`	Must be at least `k`
Row major	Must be at least `k`	Must be at least `n`

b

Buffer holding input matrix B. See Matrix Storage for more details.

	`transb` = `transpose::nontrans`	`transb` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	`B` is `k` x `n` matrix. Size of array `b` must be at least `ldb` * `n`	`B` is `n` x `k` matrix. Size of array `b` must be at least `ldb` * `k`
Row major	`B` is `k` x `n` matrix. Size of array `b` must be at least `ldb` * `k`	`B` is `n` x `k` matrix. Size of array `b` must be at least `ldb` * `n`

ldb

Leading dimension of matrix B. Must be positive.

	`transb` = `transpose::nontrans`	`transb` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	Must be at least `k`	Must be at least `n`
Row major	Must be at least `n`	Must be at least `k`

beta

Scaling factor for matrix C.

c

Buffer holding input/output matrix C. See Matrix Storage for more details.

Column major	`C` is `m` x `n` matrix. Size of array `c` must be at least `ldc` * `n`
Row major	`C` is `m` x `n` matrix. Size of array `c` must be at least `ldc` * `m`

ldc

Leading dimension of matrix C. Must be positive.

Column major	Must be at least `m`
Row major	Must be at least `n`

Output Parameters¶

c: Output buffer overwritten by upper or lower triangular part of alpha * op(A)*op(B) + beta * C.

Note

If beta = 0, matrix C does not need to be initialized before calling gemmt.

gemmt (USM Version)¶

Syntax¶

namespace oneapi::mkl::blas::column_major {
    sycl::event gemmt(sycl::queue &queue,
                      oneapi::mkl::uplo upper_lower,
                      oneapi::mkl::transpose transa,
                      oneapi::mkl::transpose transb,
                      std::int64_t n,
                      std::int64_t k,
                      T alpha,
                      const T* a,
                      std::int64_t lda,
                      const T* b,
                      std::int64_t ldb,
                      T beta,
                      T* c,
                      std::int64_t ldc,
                      const std::vector<sycl::event> &dependencies = {})
}

namespace oneapi::mkl::blas::row_major {
    sycl::event gemmt(sycl::queue &queue,
                      oneapi::mkl::uplo upper_lower,
                      oneapi::mkl::transpose transa,
                      oneapi::mkl::transpose transb,
                      std::int64_t n,
                      std::int64_t k,
                      T alpha,
                      const T* a,
                      std::int64_t lda,
                      const T* b,
                      std::int64_t ldb,
                      T beta,
                      T* c,
                      std::int64_t ldc,
                      const std::vector<sycl::event> &dependencies = {})
}

Input Parameters¶

queue

The queue where the routine should be executed.

upper_lower

Specifies whether matrix C is upper or lower triangular. See Data Types for more details.

transa

Specifies op(A), the transposition operation applied to matrix A. See Data Types for more details.

transb

Specifies op(B), the transposition operation applied to matrix B. See Data Types for more details.

n

Number of rows of matrix op(A) and matrix C. Must be at least zero.

k

Number of columns of matrix op(A) and rows of matrix op(B). Must be at least zero.

alpha

Scaling factor for matrix-matrix product.

a

Pointer to input matrix A. See Matrix Storage for more details.

	`transa` = `transpose::nontrans`	`transa` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	`A` is `n` x `k` matrix. Size of array `a` must be at least `lda` * `k`	`A` is `k` x `n` matrix. Size of array `a` must be at least `lda` * `n`
Row major	`A` is `n` x `k` matrix. Size of array `a` must be at least `lda` * `n`	`A` is `k` x `n` matrix. Size of array `a` must be at least `lda` * `k`

lda

Leading dimension of matrix A. Must be positive.

	`transa` = `transpose::nontrans`	`transa` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	Must be at least `n`	Must be at least `k`
Row major	Must be at least `k`	Must be at least `n`

b

Pointer to input matrix B. See Matrix Storage for more details.

	`transb` = `transpose::nontrans`	`transb` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	`B` is `k` x `n` matrix. Size of array `b` must be at least `ldb` * `n`	`B` is `n` x `k` matrix. Size of array `b` must be at least `ldb` * `k`
Row major	`B` is `k` x `n` matrix. Size of array `b` must be at least `ldb` * `k`	`B` is `n` x `k` matrix. Size of array `b` must be at least `ldb` * `n`

ldb

Leading dimension of matrix B. Must be positive.

	`transb` = `transpose::nontrans`	`transb` = `transpose::trans` or `trans` = `transpose::conjtrans`
Column major	Must be at least `k`	Must be at least `n`
Row major	Must be at least `n`	Must be at least `k`

beta

Scaling factor for matrix C.

c

Pointer to input/output matrix C. See Matrix Storage for more details.

Column major	`C` is `m` x `n` matrix. Size of array `c` must be at least `ldc` * `n`
Row major	`C` is `m` x `n` matrix. Size of array `c` must be at least `ldc` * `m`

ldc

Leading dimension of matrix C. Must be positive.

Column major	Must be at least `m`
Row major	Must be at least `n`

dependencies

List of events to wait for before starting computation, if any. If omitted, defaults to no dependencies.

Output Parameters¶

c: Pointer to output matrix C overwritten by upper or lower triangular part of alpha * op(A)*op(B) + beta * C.

Note

If beta = 0, matrix C does not need to be initialized before calling gemmt.

Return Values¶

Output event to wait on to ensure computation is complete.

gemm_bias gemv_batch

oneAPI Math Kernel Library (oneMKL) documentation

gemmt¶

Description¶

gemmt (Buffer Version)¶

Syntax¶

Input Parameters¶

Output Parameters¶

gemmt (USM Version)¶

Syntax¶

Input Parameters¶

Output Parameters¶

Return Values¶