Διάγραμμα Minkowski
Το διάγραμμα Minkowski αναπτύχθηκε το 1908 από τον Herman Minkowski. Απεικονίζει τις ιδιότητες του χώρου και του χρόνου στην ειδική θεωρία της σχετικότητας και επιτρέπει την ποσοτική κατανόηση φαινομένων όπως είναι η διαστολή του χρόνου και η συστολή μήκους χωρίς τη χρήση μαθηματικών εξισώσεων.
Το διάγραμμα Minkowski είναι ένα διάγραμμα χώρου-χρόνου με μόνο μία διάσταση του χώρου συνήθως. Είναι μια υπέρθεση του συντονισμού των συστημάτων δύο παρατηρητών που κινούνται μεταξύ τους με σταθερή ταχύτητα.
Το σχήμα του διαγράμματος ακολουθεί αμέσως μετά και χωρίς κανένα υπολογισμό με βάση τα αξιώματα της ειδικής σχετικότητας, καταδεικνύει τη στενή σχέση μεταξύ του χώρου και του χρόνου που ανακάλυψαν με τη θεωρία της σχετικότητας.
Για λόγους ευκολίας, τον κατακόρυφο άξονα του χρόνου αποτελεί, όχι ο χρόνος t, αλλά η αντίστοιχη ποσότητα ct, όπου c = 3×108 m/s είναι η ταχύτητα του φωτός. Η συνάρτηση x = ct ισχύει για ένα φωτόνιο που διέρχεται από τα δεξιά και είναι μια ευθεία γραμμή με κλίση 45 °, εφόσον οι κλίμακες και στους δύο άξονες είναι ίδιες.
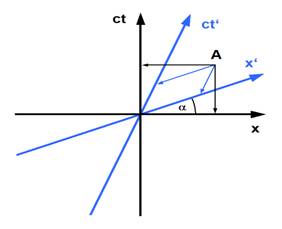Στο διάγραμμα Minkowski αυτή η σχετικότητα του ταυτόχρονου αντιστοιχεί στην εισαγωγή ενός ξεχωριστού άξονα για την κίνηση του παρατηρητή. Η αλληλουχία των γεγονότων από τη σκοπιά του παρατηρητή, μπορεί να αποδειχτεί γραφικά με τη μετατόπιση της γραμμή στο διάγραμμα από κάτω προς τα πάνω.
Από το αξίωμα 2 της ειδικής σχετικότητας προκύπτει ότι η γωνία α μεταξύ των αξόνων πρέπει να είναι ίδια είτε ο κατακόρυφος άξονας είναι t είτε ct, αφού η ταχύτητα του φωτός είναι η ίδια για όλους τους παρατηρητές, ανεξάρτητα από τη σχετική τους κίνηση. Η γωνία α δίνεται από τον τύπο:
Συνέπειες όπως ειδικής θεωρίας όπως σχετικότητας, όπως διαστολή του χρόνου και η συστολή του μήκους γίνονται φανερές και από τα διαγράμματα Minkowski.
