This section describes the Intel IPP primitives that implement arithmetic operations with elements of finite fields [ANT]. Arithmetic of the following finite fields is implemented:
G(p) |
A finite field of p elements represented by integers modulo p, where p is an odd prime number. This field is also known as a prime finite field. |
GF(p^d) |
A finite field of pd elements represented by equivalence classes modulo g(x) of polynomials whose coefficients belong to GF(p), where g(x) is an irreducible polynomial of degree d. Coefficients of g(x) are elements of the GF(p) field. This field is also known as an extension field of degree d of GF(p) or the Galois field. |
GF(p^d^2) |
A quadratic extension of GF(p^d). |
Table “Intel IPP Finite Field Arithmetic Functions” lists all the finite field arithmetic functions.
| Function Base Name | Operation |
|---|---|
| Arithmetic of Finite Fields GF(p) | |
| GFPGetSize | Gets the size of the context of a GF(p) field. |
| GFPInit | Initializes the context of a GF(p) field. |
| GFPGet | Extracts parameters of the GF(p) field from the context. |
| GFPElementGetSize | Gets the size of the context for an element of the GF(p) field. |
| GFPElementInit | Initializes the context of an element of the GF(p) field. |
| GFPSetElement | Assigns a value to an element of the GF(p) field. |
| GFPSetElementZero | Assigns the zero value to an element of the GF(p) field. |
| GFPSetElementPower2 | Assigns the value of a given power of two to an element of the GF(p) field. |
| GFPSetElementRandom | Assigns a random value to an element of the GF(p) field. |
| GFPCpyElement | Copies one element of the GF(p) field to another. |
| GFPGetElement | Extracts the element of the GF(p) field from the context. |
| GFPCmpElement | Compares elements of the GF(p) field. |
| GFPNeg | Computes the additive inverse for an element of the GF(p) field. |
| GFPInv | Computes the multiplicative inverse for an element of the GF(p) field. |
| GFPSqrt | Takes the square root of an element of the GF(p) field. |
| GFPAdd | Adds elements of the GF(p) field. |
| GFPSub | Subtracts elements of the GF(p) field. |
| GFPMul | Multiplies elements of the GF(p) field. |
| GFPExp | Exponentiates an element of the GF(p) field. |
| GFPMontEncode | Converts an element of the GF(p) field to the Montgomery residue number system. |
| GFPMontDecode | Converts an element of the GF(p) field represented in the Montgomery residue number system to the regular GF(p) element. |
| Arithmetic of Finite Fields GF(p^d) | |
| GFPXGetSize | Gets the size of the context of a GF(p^d) field. |
| GFPXInit | Initializes the context of a GF(p^d) field. |
| GFPXGet | Extracts parameters of the GF(p^d) field from the context. |
| GFPXElementGetSize | Gets the size of the context for an element of the GF(p^d) field. |
| GFPXElementInit | Initializes the context of an element of the GF(p^d) field. |
| GFPXSetElement | Assigns a value to an element of the GF(p^d) field. |
| GFPXSetElementZero | Assigns the zero value to an element of the GF(p^d) field. |
| GFPXSetElementPowerX | Assigns the value of a given power of x to an element of the GF(p^d) field. |
| GFPXSetElementRandom | Assigns a random value to an element of the GF(p^d) field. |
| GFPXCpyElement | Copies one element of the GF(p^d) field to another. |
| GFPXGetElement | Extracts the element of the GF(p^d) field from the context. |
| GFPXCmpElement | Compares elements of the GF(p^d) field. |
| GFPXNeg | Computes the additive inverse for an element of the GF(p^d) field. |
| GFPXInv | Computes the multiplicative inverse for an element of the GF(p^d) field. |
| GFPXAdd | Adds elements of the GF(p^d) field. |
| GFPXAdd_GFP | Adds elements of the GF(p^d) and GF(p) fields. |
| GFPXSub | Subtracts elements of the GF(p^d) field. |
| GFPXSub_GFP | Subtracts elements of the GF(p^d) and GF(p) fields. |
| GFPXMul | Multiplies elements of the GF(p^d) field. |
| GFPXMul_GFP | Multiplies elements of the GF(p^d) and GF(p) fields. |
| GFPXExp | Exponentiates an element of the GF(p^d) field. |
| GFPXDiv | Divides elements of the GF(p^d) field. |
| Arithmetic of Finite Fields GF(p^d^2) | |
| GFPXQGetSize | Gets the size of the context of a GF(p^d^2) field. |
| GFPXQInit | Initializes the context of a GF(p^d^2) field. |
| GFPXQGet | Extracts parameters of the GF(p^d^2) field from the context. |
| GFPXQElementGetSize | Gets the size of the context for an element of the GF(p^d^2) field. |
| GFPXQElementInit | Initializes the context of an element of the GF(p^d^2) field. |
| GFPXQSetElement | Assigns a value to an element of the GF(p^d^2) field. |
| GFPXQSetElementZero | Assigns the zero value to an element of the GF(p^d^2) field. |
| GFPXQSetElementPowerX | Assigns the value of a given power of x to an element of the GF(p^d^2) field. |
| GFPXQSetElementRandom | Assigns a random value to an element of the GF(p^d^2) field. |
| GFPXQCpyElement | Copies one element of the GF(p^d^2) field to another. |
| GFPXQGetElement | Extracts the element of the GF(p^d^2) field from the context. |
| GFPXQCmpElement | Compares elements of the GF(p^d^2) field. |
| GFPXQNeg | Computes the additive inverse for an element of the GF(p^d^2) field. |
| GFPXQInv | Computes the multiplicative inverse for an element of the GF(p^d^2) field. |
| GFPXQAdd | Adds elements of the GF(p^d^2) field. |
| GFPXQSub | Subtracts elements of the GF(p^d^2) field. |
| GFPXQMul | Multiplies elements of the GF(p^d^2) field. |
| GFPXQMul_GFP | Multiplies elements of the GF(p^d^2) and GF(p) fields. |
| GFPXQExp | Exponentiates an element of the GF(p^d^2) field. |
Each element E of GF(p) is represented
by an unsigned big number, which, in turn, is represented by a data array Ipp32u pe[length], so that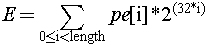
Each element E of GF(p^d) is represented by a polynomial of degree less than d, which, in turn, is represented by an array of coefficients pe[d] that belong to GF(p).
Each element E of GF(p^d^2) is represented by a polynomial of degree less than 2, which, in turn, is represented by an array of coefficients pe[2] that belong to GF(p^d).
For polynomials that represent elements of both fields, a coefficient of a lower degree is stored in an element of the respective array with a smaller index.
The Intel IPP finite field arithmetic functions use context structures of the following types to carry data of the field and field element:
GF(p) |
IppsGFPState and IppsGFPElement, respectively. |
GF(p^d) |
IppsGFPXState and IppsGFPXElement, respectively. |
GF(p^d^2) |
IppsGFPXQState and IppsGFPXQElement, respectively. |
Comparison functions GFPCmpElement, GFPXCmpElement, and GFPXQCmpElement return the result of comparison:
typedef enum {
IppsElementEQ = 0, // elements are equal
IppsElementNE = 1, // elements are not equal
IppsElementGT = 2, // the first element is greater than the second one
IppsElementLT = 3, // the first element is less than the second one
IppsElementNA = 4 // elements are not comparable
} IppsElementCmpResult;