Πώς θα μπορούσαμε να συμπεράνουμε αν ζούμε σ' ένα κόσμο επίπεδο (Ευκλείδειο) ή καμπύλο;

Ας φανταστούμε δυο δισδιάστατα όντα που ζουν πάνω σ' ένα τέτοιο στρεβλωμένο δισδιάστατο φύλλο σχήματος κούπας. Τα δισδιάστατα αυτά όντα μπορούν ν' ανακαλύψουν ότι η εξωτερική περιοχή του κόσμου τους είναι επίπεδη, ενώ η κεντρική περιοχή παρουσιάζει καμπυλότητα, εκτελώντας γεωμετρικές μετρήσεις σε κύκλους και τρίγωνα.
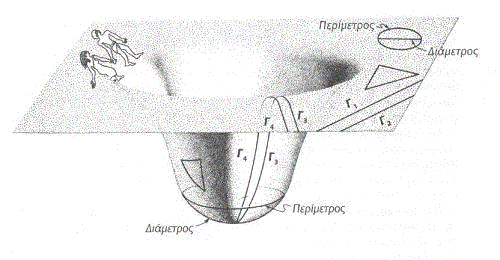Στην εξωτερική περιοχή η περίμετρος κάθε κύκλου ισούται με τη διάμετρο επί τον αριθμό π=3,14159..
Στην εσωτερική περιοχή η περίμετρος ενός κύκλου είναι μικρότερη από το παραπάνω γινόμενο.
Αν τα δισδιάστατα όντα σχεδιάσουν ένα τρίγωνο του οποίου οι πλευρές είναι ευθείες γραμμές με την έννοια των γεωδεσιακών, και στη συνέχεια υπολογίσουν το άθροισμα των εσωτερικών γωνιών του, θα πάρουν ως αποτέλεσμα 1800 στην εξωτερική επίπεδη περιοχή, και περισσότερο από 1800 στην εσωτερική στρεβλωμένη περιοχή.
Αν σχεδιάσουν επίσης δύο παράλληλες ευθείες γραμμές και τις προεκτείνουν συνεχώς, τότε θα διαπιστώσουν ότι στη μεν εξωτερική περιοχή αυτές δεν τέμνονται ποτέ, ενώ στην εσωτερική περιοχή τέμνονται στο κατώτατο σημείο της κούπας. 
Από τέτοιου είδους παρατηρήσεις μπορούμε συνεπώς να συμπεράνουμε αν ζούμε σ' ένα κόσμο επίπεδο (Ευκλείδειο) ή καμπύλο.