Διαστολή του χρόνου

Η χρονική διάρκεια ενός φαινομένου εξαρτάται από το σύστημα αναφοράς από το οποίο παρατηρούμε το φαινόμενο.

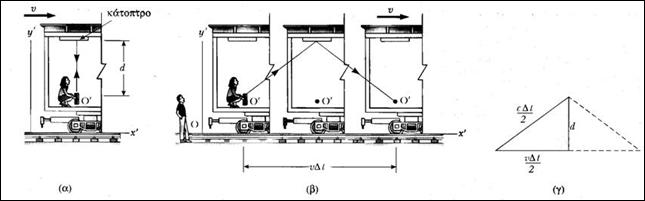
Προκειμένου να γίνει κατανοητό θα δώσουμε ένα παράδειγμα. Έστω ένα όχημα που κινείται προς τα δεξιά με ταχύτητα u, όπως δείχνει το παρακάτω σχήμα. Μέσα στο όχημα βρίσκεται ένας ακίνητος παρατηρητής στο Ο' ως προς αυτό. Στην οροφή του οχήματος έχει τοποθετηθεί ένα κάτοπτρο και ο παρατηρητής κρατάει μια λυχνία φωτεινών παλμών σε απόσταση d από το κάτοπτρο. Έστω κάποια χρονική στιγμή t η λυχνία εκπέμπει έναν φωτεινό παλμό με ταχύτητα c. Ο χρόνος Δt' που απαιτείται για την μετάβαση του φωτεινού παλμού από την λυχνία στο κάτοπτρο και την επιστροφή του στην λυχνία δίνεται από τον ορισμό της ταχύτητας ως εξής :

Ο χρόνος μετρήθηκε από το σύστημα αναφοράς του κινούμενου οχήματος (α).
Στη συνέχεια μελετάνε το ίδιο συμβάν σε ένα ακίνητο σύστημα αναφοράς από έναν παρατηρητή στο Ο. Ο παρατηρητής αυτός βλέπει το όχημα και συνεπώς την λυχνία και το κάτοπτρο να κινούνται προς τα δεξιά με ταχύτητα u. Στην περίπτωση αυτή ο χρόνος  που απαιτείται για να μεταβεί ο φωτεινός παλμός από την λυχνία στο κάτοπτρο και να επιστρέψει στην λυχνία είναι Δt. Τη στιγμή που ο φωτεινός παλμός από την λυχνία φθάνει στο κάτοπτρο, το κάτοπτρο έχει διανύσει μια απόσταση ίση με . Έτσι, ο ακίνητος παρατηρητής στο Ο  βλέποντας το σύστημα να κινείται συμπεραίνει ότι το φως πρέπει να φύγει από την λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση για να προσπέσει ξανά στο κάτοπτρο (β). Παρατηρούμε ότι στο ακίνητο σύστημα (β) το φως πρέπει να διανύσει μεγαλύτερη απόσταση απ' ότι στο κινούμενο σύστημα (α).
Όμως, σύμφωνα με τη θεωρία του Einstein η ταχύτητα του φωτός είναι ίδια και ίση με c και στα δύο συστήματα αναφοράς. Συνεπώς, το χρονικό διάστημα Δt που μετράει ο παρατηρητής στο ακίνητο σύστημα είναι μεγαλύτερο από το χρονικό διάστημα Δt' που μετράει ο παρατηρητής στο κινούμενο σύστημα αναφοράς.
Από το ορθογώνιο τρίγωνο του σχήματος (γ)  και με την εφαρμογή του Πυθαγόρειου Θεωρήματος βρίσκουμε τη σχέση που συνδέει τα χρονικά διαστήματα Δt και Δt' :   

Λύνοντας ως προς Δt έχουμε :

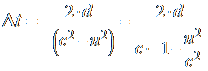
Παραπάνω βρήκαμε ότι  . Οπότε προκύπτει τελικά η σχέση:

  

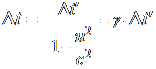
Όπου:   (το γ είναι πάντοτε μεγαλύτερο από την μονάδα).
Από την σχέση των Δt - Δt' γίνεται φανερό πως το χρονικό διάστημα που μετράται από τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από το χρονικό διάστημα που μετράται από τον παρατηρητή στο κινούμενο σύστημα. Άρα, έχουμε διαστολή του χρόνου.

να πολύ γνωστό παράδειγμα διαστολής του χρόνου είναι

• το παράδοξο των διδύμων αδελφών