Orthogonal Factorizations: LAPACK Computational Routines

This topic describes the LAPACK routines for the QR (RQ) and LQ (QL) factorization of matrices. Routines for the RZ factorization as well as for generalized QR and RQ factorizations are also included.

QR Factorization. Assume that A is an m-by-n matrix to be factored.

If m≥n, the QR factorization is given by

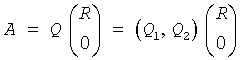
where R is an n-by-n upper triangular matrix with real diagonal elements, and Q is an m-by-m orthogonal (or unitary) matrix.

You can use the QR factorization for solving the following least squares problem: minimize ||Ax - b||² where A is a full-rank m-by-n matrix (m≥n). After factoring the matrix, compute the solution x by solving Rx = (Q₁)^Tb.

If m < n, the QR factorization is given by

A = QR = Q(R₁R₂)

where R is trapezoidal, R₁ is upper triangular and R₂ is rectangular.

Q is represented as a product of min(m, n) elementary reflectors. Routines are provided to work with Q in this representation.

LQ Factorization LQ factorization of an m-by-n matrix A is as follows. If m≤n,

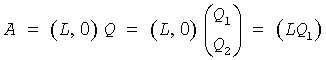
where L is an m-by-m lower triangular matrix with real diagonal elements, and Q is an n-by-n orthogonal (or unitary) matrix.

If m > n, the LQ factorization is

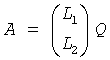
where L₁ is an n-by-n lower triangular matrix, L₂ is rectangular, and Q is an n-by-n orthogonal (or unitary) matrix.

You can use the LQ factorization to find the minimum-norm solution of an underdetermined system of linear equations Ax = b where A is an m-by-n matrix of rank m (m < n). After factoring the matrix, compute the solution vector x as follows: solve Ly = b for y, and then compute x = (Q₁)^Hy.

Table "Computational Routines for Orthogonal Factorization" lists LAPACK routines that perform orthogonal factorization of matrices.