?tpqrt

Syntax

lapack_int LAPACKE_stpqrt (int matrix_layout, lapack_int m, lapack_int n, lapack_int l, lapack_int nb, float* a, lapack_int lda, float* b, lapack_int ldb, float* t, lapack_int ldt);

lapack_int LAPACKE_dtpqrt (int matrix_layout, lapack_int m, lapack_int n, lapack_int l, lapack_int nb, double* a, lapack_int lda, double* b, lapack_int ldb, double* t, lapack_int ldt);

lapack_int LAPACKE_ctpqrt (int matrix_layout, lapack_int m, lapack_int n, lapack_int l, lapack_int nb, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* t, lapack_int ldt);

lapack_int LAPACKE_ztpqrt (int matrix_layout, lapack_int m, lapack_int n, lapack_int l, lapack_int nb, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* t, lapack_int ldt);

Include Files

• mkl.h

Description

The input matrix C is an (n+m)-by-n matrix

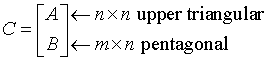
where A is an n-by-n upper triangular matrix, and B is an m-by-n pentagonal matrix consisting of an (m-l)-by-n rectangular matrix B1 on top of an l-by-n upper trapezoidal matrix B2:

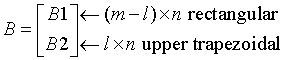
The upper trapezoidal matrix B2 consists of the first l rows of an n-by-n upper triangular matrix, where 0 ≤ l ≤ min(m,n). If l=0, B is an m-by-n rectangular matrix. If m=l=n, B is upper triangular. The elementary reflectors H(i) are stored in the ith column below the diagonal in the (n+m)-by-n input matrix C. The structure of vectors defining the elementary reflectors is illustrated by:

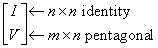
The elements of the unit matrix I are not stored. Thus, V contains all of the necessary information, and is returned in array b.

Note

Note that V has the same form as B:

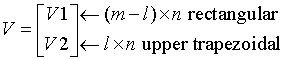
The columns of V represent the vectors which define the H(i)s.

The number of blocks is k = ceiling(n/nb), where each block is of order nb except for the last block, which is of order ib = n - (k-1)*nb. For each of the k blocks, an upper triangular block reflector factor is computed: T1, T2, ..., Tk. The nb-by-nb (ib-by-ib for the last block) Tis are stored in the nb-by-n array t as

t = [T1T2 ... Tk] .

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The total number of rows in the matrix B (m ≥ 0).

n

The number of columns in B and the order of the triangular matrix A (n ≥ 0).

l

The number of rows of the upper trapezoidal part of B (min(m, n) ≥ l ≥ 0).

nb

The block size to use in the blocked QR factorization (n ≥ nb ≥ 1).

a, b

Arrays: a size lda*n contains the n-by-n upper triangular matrix A.

b size max(1, ldb*n) for column major layout and max(1, ldb*m) for row major layout, the pentagonal m-by-n matrix B. The first (m-l) rows contain the rectangular B1 matrix, and the next l rows contain the upper trapezoidal B2 matrix.

lda

The leading dimension of a; at least max(1, n).

ldb

The leading dimension of b; at least max(1, m) for column major layout and at least max(1, n) for row major layout.

ldt

The leading dimension of t; at least nb for column major layout and at least max(1, n) for row major layout.

Output Parameters

a

The elements on and above the diagonal of the array contain the upper triangular matrix R.

b

The pentagonal matrix V.

t

Array, size ldt*n for column major layout and ldt*nb for row major layout.

The upper triangular block reflectors stored in compact form as a sequence of upper triangular blocks.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.