?bbcsd

Syntax

lapack_int LAPACKE_sbbcsd( int matrix_layout, char jobu1, char jobu2, char jobv1t, char jobv2t, char trans, lapack_int m, lapack_int p, lapack_int q, float* theta, float* phi, float* u1, lapack_int ldu1, float* u2, lapack_int ldu2, float* v1t, lapack_int ldv1t, float* v2t, lapack_int ldv2t, float* b11d, float* b11e, float* b12d, float* b12e, float* b21d, float* b21e, float* b22d, float* b22e );

lapack_int LAPACKE_dbbcsd( int matrix_layout, char jobu1, char jobu2, char jobv1t, char jobv2t, char trans, lapack_int m, lapack_int p, lapack_int q, double* theta, double* phi, double* u1, lapack_int ldu1, double* u2, lapack_int ldu2, double* v1t, lapack_int ldv1t, double* v2t, lapack_int ldv2t, double* b11d, double* b11e, double* b12d, double* b12e, double* b21d, double* b21e, double* b22d, double* b22e );

lapack_int LAPACKE_cbbcsd( int matrix_layout, char jobu1, char jobu2, char jobv1t, char jobv2t, char trans, lapack_int m, lapack_int p, lapack_int q, float* theta, float* phi, lapack_complex_float* u1, lapack_int ldu1, lapack_complex_float* u2, lapack_int ldu2, lapack_complex_float* v1t, lapack_int ldv1t, lapack_complex_float* v2t, lapack_int ldv2t, float* b11d, float* b11e, float* b12d, float* b12e, float* b21d, float* b21e, float* b22d, float* b22e );

lapack_int LAPACKE_zbbcsd( int matrix_layout, char jobu1, char jobu2, char jobv1t, char jobv2t, char trans, lapack_int m, lapack_int p, lapack_int q, double* theta, double* phi, lapack_complex_double* u1, lapack_int ldu1, lapack_complex_double* u2, lapack_int ldu2, lapack_complex_double* v1t, lapack_int ldv1t, lapack_complex_double* v2t, lapack_int ldv2t, double* b11d, double* b11e, double* b12d, double* b12e, double* b21d, double* b21e, double* b22d, double* b22e );

Include Files

• mkl.h

Description

mkl_lapack.fiThe routine ?bbcsd computes the CS decomposition of an orthogonal or unitary matrix in bidiagonal-block form:

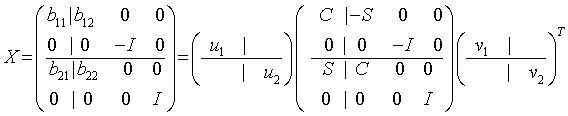
or

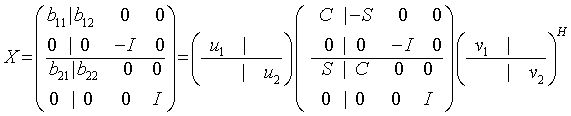
respectively.

x is m-by-m with the top-left block p-by-q. Note that q must not be larger than p, m-p, or m-q. If q is not the smallest index, x must be transposed and/or permuted in constant time using the trans option. See ?orcsd/?uncsd for details.

The bidiagonal matrices b₁₁, b₁₂, b₂₁, and b₂₂ are represented implicitly by angles theta(1:q) and phi(1:q-1).

The orthogonal/unitary matrices u₁, u₂, v₁^t, and v₂^t are input/output. The input matrices are pre- or post-multiplied by the appropriate singular vector matrices.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

jobu1

If equals Y, then u₁ is updated. Otherwise, u₁ is not updated.

jobu2

If equals Y, then u₂ is updated. Otherwise, u₂ is not updated.

jobv1t

If equals Y, then v₁^t is updated. Otherwise, v₁^t is not updated.

jobv2t

If equals Y, then v₂^t is updated. Otherwise, v₂^t is not updated.

trans

= 'T':

x, u₁, u₂, v₁^t, v₂^t are stored in row-major order.

otherwise

x, u₁, u₂, v₁^t, v₂^t are stored in column-major order.

m

The number of rows and columns of the orthogonal/unitary matrix X in bidiagonal-block form.

p

The number of rows in the top-left block of x. 0 ≤p≤m.

≤

q

The number of columns in the top-left block of x. 0 q≤ min(p,m-p,m-q).

theta

Array, size q.

On entry, the angles theta[0], ..., theta[q - 1] that, along with phi[0], ..., phi[q - 2], define the matrix in bidiagonal-block form as returned by orbdb/unbdb.

phi

Array, size q-1.

The angles phi[0], ..., phi[q - 2] that, along with theta[0], ..., theta[q - 1], define the matrix in bidiagonal-block form as returned by orbdb/unbdb.

u1

Array, size at least max(1, ldu1*p).

On entry, a p-by-p matrix.

ldu1

The leading dimension of the array u₁, ldu1≤ max(1, p).

u2

Array, size max(1, ldu2*(m-p)).

On entry, an (m-p)-by-(m-p) matrix.

ldu2

The leading dimension of the array u₂, ldu2≤ max(1, m-p).

v1t

Array, size max(1, ldv1t*q).

On entry, a q-by-q matrix.

ldv1t

The leading dimension of the array v1t, ldv1t≤ max(1, q).

v2t

Array, size.

On entry, an (m-q)-by-(m-q) matrix.

ldv2t

The leading dimension of the array v2t, ldv2t≤ max(1, m-q).

Output Parameters

theta

On exit, the angles whose cosines and sines define the diagonal blocks in the CS decomposition.

u1

On exit, u1 is postmultiplied by the left singular vector matrix common to [ b11 ; 0 ] and [ b12 0 0 ; 0 -I 0 ].

u2

On exit, u2 is postmultiplied by the left singular vector matrix common to [ b21 ; 0 ] and [ b22 0 0 ; 0 0 I ].

v1t

Array, size q.

On exit, v1t is premultiplied by the transpose of the right singular vector matrix common to [ b11 ; 0 ] and [ b21 ; 0 ].

v2t

On exit, v2t is premultiplied by the transpose of the right singular vector matrix common to [ b12 0 0 ; 0 -I 0 ] and [ b22 0 0 ; 0 0 I ].

b11d

Array, size q.

When ?bbcsd converges, b11d contains the cosines of theta[0], ..., theta[q - 1]. If ?bbcsd fails to converge, b11d contains the diagonal of the partially reduced top left block.

b11e

Array, size q-1.

When ?bbcsd converges, b11e contains zeros. If ?bbcsd fails to converge, b11e contains the superdiagonal of the partially reduced top left block.

b12d

Array, size q.

When ?bbcsd converges, b12d contains the negative sines of theta[0], ..., theta[q - 1]. If ?bbcsd fails to converge, b12d contains the diagonal of the partially reduced top right block.

b12e

Array, size q-1.

When ?bbcsd converges, b12e contains zeros. If ?bbcsd fails to converge, b11e contains the superdiagonal of the partially reduced top right block.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info > 0 and if ?bbcsd did not converge, info specifies the number of nonzero entries in phi, and b11d, b11e, etc. contain the partially reduced matrix.