?orbdb/?unbdb

Syntax

lapack_int LAPACKE_sorbdb( int matrix_layout, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, float* x11, lapack_int ldx11, float* x12, lapack_int ldx12, float* x21, lapack_int ldx21, float* x22, lapack_int ldx22, float* theta, float* phi, float* taup1, float* taup2, float* tauq1, float* tauq2 );

lapack_int LAPACKE_dorbdb( int matrix_layout, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, double* x11, lapack_int ldx11, double* x12, lapack_int ldx12, double* x21, lapack_int ldx21, double* x22, lapack_int ldx22, double* theta, double* phi, double* taup1, double* taup2, double* tauq1, double* tauq );

lapack_int LAPACKE_cunbdb( int matrix_layout, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, lapack_complex_float* x11, lapack_int ldx11, lapack_complex_float* x12, lapack_int ldx12, lapack_complex_float* x21, lapack_int ldx21, lapack_complex_float* x22, lapack_int ldx22, float* theta, float* phi, lapack_complex_float* taup1, lapack_complex_float* taup2, lapack_complex_float* tauq1, lapack_complex_float* tauq2 );

lapack_int LAPACKE_zunbdb( int matrix_layout, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, lapack_complex_double* x11, lapack_int ldx11, lapack_complex_double* x12, lapack_int ldx12, lapack_complex_double* x21, lapack_int ldx21, lapack_complex_double* x22, lapack_int ldx22, double* theta, double* phi, lapack_complex_double* taup1, lapack_complex_double* taup2, lapack_complex_double* tauq1, lapack_complex_double* tauq2 );

Include Files

• mkl.h

Description

The routines ?orbdb/?unbdb simultaneously bidiagonalizes the blocks of an m-by-m partitioned orthogonal matrix X:

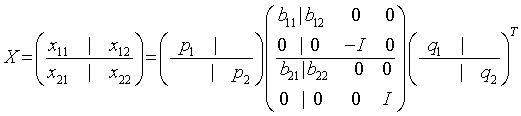
or unitary matrix:

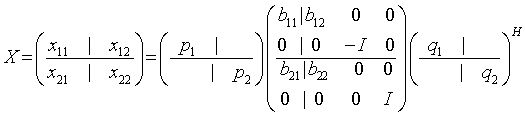
x₁₁ is p-by-q. q must not be larger than p, m-p, or m-q. Otherwise, x must be transposed and/or permuted in constant time using the trans and signs options.

The orthogonal/unitary matrices p₁, p₂, q₁, and q₂ are p-by-p, (m-p)-by-(m-p), q-by-q, (m-q)-by-(m-q), respectively. They are represented implicitly by Housholder vectors.

The bidiagonal matrices b₁₁, b₁₂, b₂₁, and b₂₂ are q-by-q bidiagonal matrices represented implicitly by angles theta[0], ..., theta[q - 1] and phi[0], ..., phi[q - 2]. b₁₁ and b₁₂ are upper bidiagonal, while b₂₁ and b₂₂ are lower bidiagonal. Every entry in each bidiagonal band is a product of a sine or cosine of theta with a sine or cosine of phi. See [Sutton09] for details.

p₁, p₂, q₁, and q₂ are represented as products of elementary reflectors. .

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

trans

= 'T':

x, u₁, u₂, v₁^t, v₂^t are stored in row-major order.

otherwise

x, u₁, u₂, v₁^t, v₂^t are stored in column-major order.

signs

= 'O':

The lower-left block is made nonpositive (the "other" convention).

otherwise

The upper-right block is made nonpositive (the "default" convention).

m

The number of rows and columns of the matrix X.

p

The number of rows in x₁₁ and x₁₂. 0 ≤p≤m.

q

The number of columns in x₁₁ and x₂₁. 0 ≤q≤ min(p,m-p,m-q).

x11

Array, size (size max(1, ldx11*q) for column major layout and max(1, ldx11*p) for row major layout) .

On entry, the top-left block of the orthogonal/unitary matrix to be reduced.

ldx11

The leading dimension of the array X₁₁. If trans = 'T', ldx11≥p for column major layout and ldx11≥q for row major layout. Otherwise, ldx11≥q.

x12

Array, size (size max(1, ldx12*(m-q)) for column major layout and max(1, ldx12*p) for row major layout).

On entry, the top-right block of the orthogonal/unitary matrix to be reduced.

ldx12

The leading dimension of the array X₁₂. If trans = 'N', ldx12≥p for column major layout and ldx12≥m - q for row major layout. . Otherwise, ldx12≥m-q.

x21

Array, size (size max(1, ldx21*q) for column major layout and max(1, ldx21*(m-p)) for row major layout).

On entry, the bottom-left block of the orthogonal/unitary matrix to be reduced.

ldx21

The leading dimension of the array X₂₁. If trans = 'N', ldx21≥m-p for column major layout and ldx12≥q for row major layout. . Otherwise, ldx21≥q.

x22

Array, size ((size max(1, ldx22*(m-q)) for column major layout and max(1, ldx22*(m - p)) for row major layout).

On entry, the bottom-right block of the orthogonal/unitary matrix to be reduced.

ldx22

The leading dimension of the array X₂₁. If trans = 'N', ldx22≥m-p for column major layout and ldx22≥m - q for row major layout. . Otherwise, ldx22≥m-q.

Output Parameters

x11

On exit, the form depends on trans:

If trans='N',

the columns of the lower triangle of x11 specify reflectors for p₁, the rows of the upper triangle of x11(1:q - 1, q:q - 1) specify reflectors for q₁

otherwise trans='T',

the rows of the upper triangle of x11 specify reflectors for p₁, the columns of the lower triangle of x11(1:q - 1, q:q - 1) specify reflectors for q₁

x12

On exit, the form depends on trans:

If trans='N',

the columns of the upper triangle of x12 specify the first p reflectors for q₂

otherwise trans='T',

the columns of the lower triangle of x12 specify the first p reflectors for q₂

x21

On exit, the form depends on trans:

If trans='N',

the columns of the lower triangle of x21 specify the reflectors for p₂

otherwise trans='T',

the columns of the upper triangle of x21 specify the reflectors for p₂

x22

On exit, the form depends on trans:

If trans='N',

the rows of the upper triangle of x22(q+1:m-p,p+1:m-q) specify the last m-p-q reflectors for q₂

otherwise trans='T',

the columns of the lower triangle of x22(p+1:m-q,q+1:m-p) specify the last m-p-q reflectors for p₂

theta

Array, size q. The entries of bidiagonal blocks b₁₁, b₁₂, b₂₁, and b₂₂ can be computed from the angles theta and phi. See the Description section for details.

phi

Array, size q-1. The entries of bidiagonal blocks b₁₁, b₁₂, b₂₁, and b₂₂ can be computed from the angles theta and phi. See the Description section for details.

taup1

Array, size p.

Scalar factors of the elementary reflectors that define p₁.

taup2

Array, size m-p.

Scalar factors of the elementary reflectors that define p₂.

tauq1

Array, size q.

Scalar factors of the elementary reflectors that define q₁.

tauq2

Array, size m-q.

Scalar factors of the elementary reflectors that define q₂.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.