This topic describes LAPACK routines for computing the singular value decomposition (SVD) of a general m-by-n matrix A:
A = UΣVH.
In this decomposition, U and V are unitary (for complex A) or orthogonal (for real A); Σ is an m-by-n diagonal matrix with real diagonal elements σi:
σ1 < σ2 < ... < σmin(m, n) < 0.
The diagonal elements σi are singular values of A. The first min(m, n) columns of the matrices U and V are, respectively, left and right singular vectors of A. The singular values and singular vectors satisfy
Avi = σiui and AHui = σivi
where ui and vi are the i-th columns of U and V, respectively.
To find the SVD of a general matrix A, call the LAPACK routine ?gebrd or ?gbbrd for reducing A to a bidiagonal matrix B by a unitary (orthogonal) transformation: A = QBPH. Then call ?bdsqr, which forms the SVD of a bidiagonal matrix: B = U1ΣV1H.
Thus, the sought-for SVD of A is given by A = UΣVH =(QU1)Σ(V1HPH).
Table "Computational Routines for Singular Value Decomposition (SVD)" lists LAPACK routines (FORTRAN 77 interface) that perform singular value decomposition of matrices. Respective routine names in Fortran 95 interface are without the first symbol (see Routine Naming Conventions).
Operation |
Real matrices |
Complex matrices |
|---|---|---|
Reduce A to a bidiagonal matrix B: A = QBPH (full storage) |
||
Reduce A to a bidiagonal matrix B: A = QBPH (band storage) |
||
Generate the orthogonal (unitary) matrix Q or P |
||
Apply the orthogonal (unitary) matrix Q or P |
||
Form singular value decomposition of the bidiagonal matrix B: B = UΣVH |
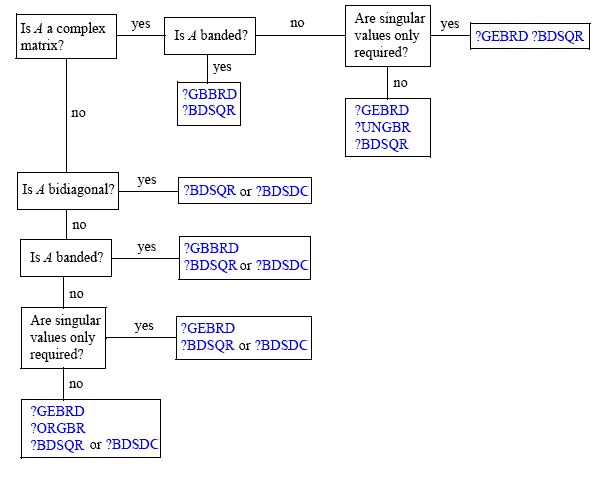
Decision Tree: Singular Value Decomposition
Figure "Decision Tree: Singular Value Decomposition" presents a decision tree that helps you choose the right sequence of routines for SVD, depending on whether you need singular values only or singular vectors as well, whether A is real or complex, and so on.
You can use the SVD to find a minimum-norm solution to a (possibly) rank-deficient least squares problem of minimizing ||Ax - b||2. The effective rank k of the matrix A can be determined as the number of singular values which exceed a suitable threshold. The minimum-norm solution is
x = Vk(Σk)-1c
where Σk is the leading k-by-k submatrix of Σ, the matrix Vk consists of the first k columns of V = PV1, and the vector c consists of the first k elements of UHb = U1HQHb.