DFTI_INPUT_STRIDES, DFTI_OUTPUT_STRIDES

The FFT interface provides configuration parameters that define the layout of multidimensional data in the computer memory. For d-dimensional data set X defined by dimensions N₁ x N₂ x ... x N_d, the layout describes where a particular element X(k₁, k₂, ..., k_d) of the data set is located. The memory address of the element X(k₁, k₂ , ..., k_d) is expressed by the formula

    address of X(k₁, k₂, ..., k_d) = address of X(0, 0, ..., 0) + offset

                                                     = address of X(0, 0, ..., 0) + s₀ + k₁*s₁ + k₂*s₂ + ...+ k_d*s_d,

where s₀ is the displacement and s₁, ..., s_d are generalized strides. The configuration parameters DFTI_INPUT_STRIDES and DFTI_OUTPUT_STRIDES enable you to get and set these values. The configuration value is an array of values (s₀, s₁, ..., s_d) of INTEGER data type in Fortran and MKL_LONG data type in C.

The offset is counted in elements of the data type defined by the descriptor configuration (rather than by the type of the variable passed to the computation functions). Specifically, the DFTI_FORWARD_DOMAIN, DFTI_COMPLEX_STORAGE, and DFTI_CONJUGATE_EVEN_STORAGE configuration parameters define the type of the elements as shown in Table "Assumed Element Types of the Input/Output Data":

The DFTI_INPUT_STRIDES configuration parameter describes the layout of the input data, and the element type is defined by the forward domain for the DftiComputeForward function, and by the backward domain for the DftiComputeBackward function. The DFTI_OUTPUT_STRIDES configuration parameter describes the layout of the output data, and the element type is defined by the backward domain for the DftiComputeForward function, and by the forward domain for DftiComputeBackward function.

For in-place transforms, the configuration set by DFTI_OUTPUT_STRIDES is ignored except when the element types in forward and backward domains are different. If they are different, set DFTI_OUTPUT_STRIDES explicitly (even though the transform is in-place). For in-place transforms, the configuration must be consistent, that is, the locations of the first elements in input and output must coincide in each dimension. The DFTI_PLACEMENT configuration parameter defines whether the transform is in-place or out-of-place.

The configuration parameters define the layout of input and output data, and not the forward-domain and backward-domain data. If the data layouts in forward domain and backward domain differ, set DFTI_INPUT_STRIDES and DFTI_OUTPUT_STRIDES explicitly and then commit the descriptor before calling computation functions.

The FFT interface supports both positive and negative stride values. If you use negative strides, set the displacement of the data as follows:

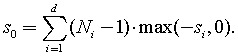
The default setting of strides in a general multi-dimensional case assumes that the array that contains the data has no padding. The order of the strides depends on the programming language. For example:

/* C/C++ */
MKL_LONG dims[] = { nd, …, n2, n1 };
DftiCreateDescriptor( &hand, precision, domain, d, dims );
// The above call assumes data declaration:  type X[nd]…[n2][n1]
// Default strides are { 0, nd*…*n2*n1, …,  n2*n1, n1, 1 }

! Fortran
INTEGER :: dims(d) = [n1, n2, …, nd]
status = DftiCreateDescriptor( hand, precision, domain, d, dims)
! The above call assumes data declaration:  type X(n1,n2,…,nd) 
! Default strides are [ 0, 1, n1, n1*n2, …, n1*n2*…*nd]

Note that in case of a real FFT (DFTI_DOMAIN=DFTI_REAL), where different data layouts in the backward domain are available (see DFTI_PACKED_FORMAT), the default value of the strides is not intuitive for the recommended CCE format (configuration setting DFTI_CONJUGATE_EVEN_STORAGE=DFTI_COMPLEX_COMPLEX). In case of an in-place real transform with the CCE format, set the strides explicitly, as follows:

/* C/C++ */
MKL_LONG dims[] = { nd, …, n2, n1 };
MKL_LONG rstrides[] = { 0, nd*…*n2*(n1/2+1), …, 2*n2*(n1/2+1), 2*(n1/2+1), 1 };
MKL_LONG cstrides[] = { 0, nd*…*n2*(n1/2+1), …, n2*(n1/2+1), (n1/2+1), 1 };
DftiCreateDescriptor( &hand, precision,  DFTI_REAL, d, dims );
DftiSetValue(hand, DFTI_CONJUGATE_EVEN_STORAGE, DFTI_COMPLEX_COMPLEX);
// Set the strides appropriately for forward/backward transform

! Fortran
INTEGER :: dims(d) = [n1, n2, …, nd]
INTEGER :: rstrides(1+d) = [0, 1, 2*(n1/2+1), 2*(n1/2+1)*n2, … ]
INTEGER :: cstrides(1+d) = [0, 1, (n1/2+1), (n1/2+1)*n2, … ]
status = DftiCreateDescriptor( hand, precision, domain, d, dims)
status = DftiSetValue( hand, DFTI_CONJUGATE_EVEN_STORAGE, DFTI_COMPLEX_COMPLEX)
! Set the strides appropriately for forward/backward transform