Intel® IPP implements image processing functions that perform two-dimensional discrete wavelet transform (DWT).
In many applications the multiresolution analysis by discrete wavelet transforms is a better alternative to windowing and discrete Fourier analysis techniques. On the one hand, the forward two-dimensional wavelet transform may be considered as a decomposition of an image on the base of functions bounded or localized in space; and on the other, the wavelet transforms are related to subband filtering and resampling.
Intel IPP for image processing contains one-level discrete wavelet decomposition and reconstruction functions. It also provides the necessary interface for initialization and deallocation of the transform context structure. Table “Image Wavelet Transform Functions” lists all functions of this group:
| Function Base Name | Operation |
|---|---|
| WTFwdInitAlloc | Allocates memory and initializes the forward wavelet transform context structure |
| WTFwdFree | Deallocates memory allocated for a forward wavelet transform context structure |
| WTFwdGetBufSize | Determines the size of external work buffer for a forward wavelet transform |
| WTFwd | Performs one-level wavelet decomposition of an image |
| WTInvInitAlloc | Allocates memory and initializes the inverse wavelet transform context structure |
| WTInvFree | Deallocates memory allocated for an inverse wavelet transform context structure |
| WTInvGetBufSize | Determines the size of external work buffer for an inverse wavelet transform |
| WTInv | Performs one-level wavelet reconstruction of an image |
The wavelet transform type can be set by specifying the appropriate filter taps in the initialization function.
Note that Intel IPP supports only one-dimensional finite impulse response filters for separable convolution.
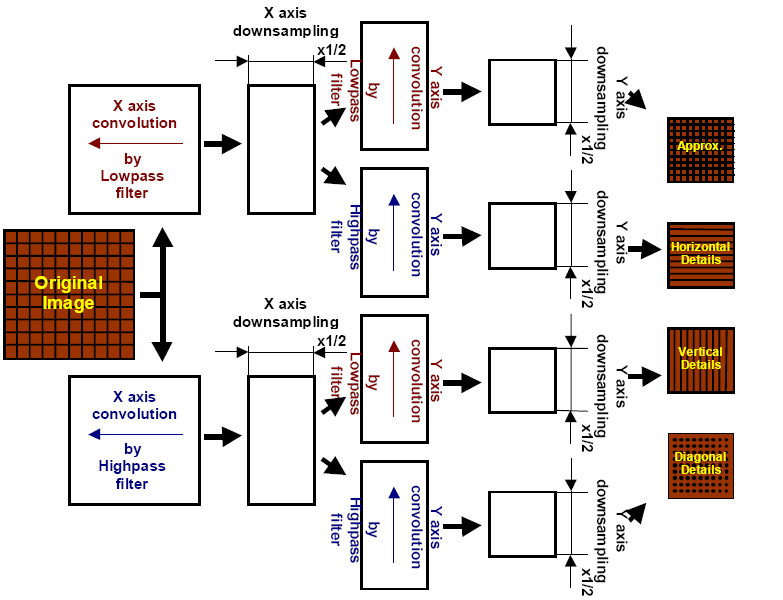
The Intel IPP functions for wavelet decomposition and reconstruction use fast polyphase algorithm, which is equivalent to traditional application of separable convolution and dyadic resampling in different order. Figure “Equivalent Scheme of Wavelet Decomposition Algorithm” shows the equivalent algorithm of wavelet-based image decomposition:
Decomposition operation applied to a source image produces four output images of equal size: approximation image, horizontal detail image, vertical detail image, and diagonal detail image.
These decomposition components have the following meaning:
- The ‘approximation' image is obtained by vertical and horizontal lowpass filtering.
- The ‘horizontal detail' image is obtained by vertical highpass and horizontal lowpass filtering.
- The ‘vertical detail' image is obtained by vertical lowpass and horizontal highpass filtering.
- The ‘diagonal detail' image is obtained by vertical and horizontal highpass filtering.
The above image names are used in this manual for identification convenience only.
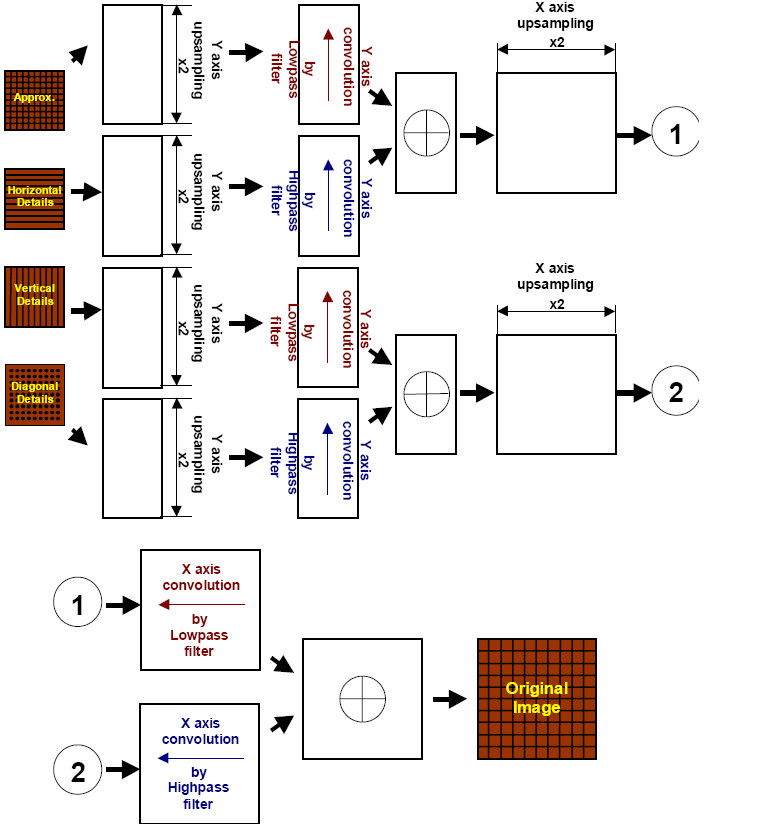
The wavelet-based image reconstruction can be represented by a sequence of separate convolution and dyadic upsampling.
The reconstruction function uses four input images that are the same as those resulting from the decomposition operation.
Figure “Equivalent Scheme of Wavelet Reconstruction Algorithm” shows the equivalent algorithm of wavelet reconstruction of an image.
Wavelet transform functions support regions of interest (ROI, see Regions of Interest in Intel IPP) in the images. However, these functions do not perform internally any border extensions of image ROI data. It means that source images must already contain all border data that are necessary for convolution operations. See descriptions of the functions ippiWTFwd and ippiWTInv for detailed information on how to calculate extended image border sizes.
The use of Intel IPP for wavelet transform is demonstrated in the Wavelet Transform Sample. In addition to this sample many solutions and hints for use of Intel IPP in wavelet applications can be found in the JPEG 2000 Encode-Decode Sample. Both samples can be downloaded from http://www.intel.com/cd/software/products/asmo-na/eng/220046.htm.