Computational Physics
A Practical Introduction to Computational
Physics and Scientific Computing
Konstantinos N. Anagnostopoulos
National Technical University
COMPUTATIONAL PHYSICS
A Practical Introduction to Computational Physics and Scientific Computing
AUTHORED BY KONSTANTINOS N. ANAGNOSTOPOULOS
Physics Department, National Technical University of Athens, Zografou Campus, 15780 Zografou,
Greece
konstant@mail.ntua.gr, www.physics.ntua.gr/~konstant/
PUBLISHED BY KONSTANTINOS N. ANAGNOSTOPOULOS
and the
NATIONAL TECHNICAL UNIVERSITY OF ATHENS
Book Website:
www.physics.ntua.gr/~konstant/ComputationalPhysics
©Konstantinos N. Anagnostopoulos 2014, 2016
First Published 2014
Version
1.1.20161207100600
Cover: Design by K.N. Anagnostopoulos. The front cover picture is a snapshot taken during Monte Carlo
simulations of hexatic membranes. Work done with Mark J. Bowick. Relevant video at youtu.be/Erc7Q6YXfLk
 This book and its cover(s) are subject to copyright. They are licensed under the Creative Commons
Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit
This book and its cover(s) are subject to copyright. They are licensed under the Creative Commons
Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit
creativecommons.org/licenses/by-sa/4.0/
The book is accompanied by software available at the book’s website. All the software, unless the copyright does
not belong to the author, is open source, covered by the GNU public license, see www.gnu.org/licenses/. This is
explicitly mentioned at the end of the respective source files.
ISBN 978-1-312-46441-4 (lulu.com, vol. I)
ISBN 978-1-312-46488-9 (lulu.com, vol. II)
Contents
This book has been written assuming that the reader executes all
the commands presented in the text and follows all the
instructions at the same time. If this advice is neglected, then
the book will be of little help and some parts of the text may seem
incomprehensible.
The book’s website is at
http://www.physics.ntua.gr/~konstant/ComputationalPhysics/
From there, you can can download the accompanying software, which
contains, among other things, all the programs presented in the book.
Some conventions: Text using the font shown below refers to commands
given using a shell (the “command line”), input and output of programs, code
written in Fortran (or any other programming language), as well as to names of
files and programs:
> echo Hello world
Hello world
When a line starts with the prompt
>
then the text that follows is a command, which can be given from the command
line of a terminal. The second line, Hello World, is the output of the
command.
The contents of a file with Fortran code is listed below:
program add
z = 1.0
y = 2.0
x = z + y
print *, x
end program add
What you need in order to work on your PC:
- An operating system of the GNU/Linux family and its basic tools.
- A Fortran compiler. The gfortran compiler is freely available
for all major operating systems under an open source license at
http://www.gfortran.org.
- An advanced text editor, suitable for editing code in several programming
languages, like Emacs .
- A good plotting program, suitable for data analysis, like gnuplot .
- The shell tcsh .
- The programs awk ,
grep, sort, cat, head, tail, less. Make sure that they are available
in your computer environment.
If you have installed a GNU/Linux distribution on your computer, all of the
above can be installed easily. For example, in a Debian like distribution (Ubuntu,
...) the commands
> sudo apt-get install tcsh emacs gnuplot-x11 gnuplot-doc
> sudo apt-get install gfortran gawk gawk-doc binutils
> sudo apt-get install manpages-dev coreutils liblapack3
install all the necessary tools.
If you don’t wish to install GNU/Linux on your computer, you can try the
following:
- Boot your computer using a usb/DVD live GNU/Linux, like Ubuntu .
This will not make any permanent changes in your hard drive but it
will start and run slower. On the other hand, you may save all your
computing environment and documents and use it on any computer
you like.
- Install Cygwin
in your Microsoft Windows. It is a very good solution for Microsoft-addicted
users. If you choose the full installation, then you will find all the tools
needed in this book.
- Mac OS X is based on Unix. It is possible to install all the software
needed in this book and follow the material as presented. Search the
internet for instructions, e.g. google “gfortran for Mac”, “emacs for
Mac”, “tcsh for Mac”, etc.
Foreword
This book is the culmination of my ten years’ experience in teaching three
introductory, undergraduate level, scientific computing/computational physics
classes at the National Technical University of Athens. It is suitable mostly
for junior or senior level science courses, but I am currently teaching its
first chapters to sophomores without a problem. A two semester course
can easily cover all the material in the book, including lab sessions for
practicing.
Why another book in computational physics? Well, when I started teaching
those classes there was no bibliography available in Greek, so I was compelled to
write lecture notes for my students. Soon, I realized that my students, majoring in
physics or applied mathematics, were having a hard time with the technical
details of programming and computing, rather than with the physics concepts. I
had to take them slowly by the hand through the “howto” of computing,
something that is reflected in the philosophy of this book. Hoping that this could
be useful to a wider audience, I decided to translate these notes in English
and put them in an order and structure that would turn them into “a
book”.
I also decided to make the book freely available on the web. I was
partly motivated by my anger caused by the increase of academic (e)book
prices to ridiculous levels during times of plummeting publishing costs.
Publishers play a diminishing role in academic publishing. They get an almost
ready-made manuscript in electronic form by the author. They need to
take no serious investment risk on an edition, thanks to print-on-demand
capabilities. They have virtually zero cost ebook publishing. Moreover, online
bookstores have decreased costs quite a lot. Academic books need no
advertisement budget, their success is due to their academic reputation. I don’t
see all of these reflected on reduced book prices, quite the contrary, I’m
afraid.
My main motivation, however, is the freedom that independent publishing
would give me in improving, expanding and changing the book in the future. It is
great to have no length restrictions for the presentation of the material, as well as
not having to report to a publisher. The reader/instructor that finds the book
long, can read/print the portion of the book that she finds useful for
her.
This is not a reference book. It uses some interesting, I hope, physics problems
in order to introduce the student to the fundamentals of solving a scientific
problem numerically. At the same time, it keeps an eye in the direction of
advanced and high performance scientific computing. The reader should follow the
instructions given in each chapter, since the book teaches by example. Several
skills are taught through the solution of a particular problem. My lectures take
place in a (large) computer lab, where the students are simultaneously doing
what I am doing (and more). The program that I am editing and the
commands that I am executing are shown on a large screen, displaying my
computer monitor and actions live. The book provides no systematic
teaching of a programming language or a particular tool. A very basic
introduction is given in the first chapter and then the reader learns whatever is
necessary for the solution of her problem. There is more than one way to do
it
and the problems can be solved by following a basic or a fancy way, depending on
the student’s computational literacy. The book provides the necessary tools for
both. A bibliography is provided at the end of the book, so that the missing pieces
of a puzzle can be sought in the literature.
This is also not a computational physics playground. Of course I hope that the
reader will have fun doing what is in the book, but my goal is to provide an
experience that will set the solid foundation for her becoming a high performance
computing, number crunching, heavy duty data analysis expert in the future. This
is why the programming language of the core numerical algorithms has
been chosen to be Fortran, a highly optimized, scientifically oriented,
programming language. The computer environment is set in a Unix family
operating system, enriched by all the powerful GNU tools provided by the
FSF .
These tools are indispensable in the complicated data manipulation needed in
scientific research, which requires flexibility and imagination. Of course,
Fortran is not the best choice for heavy duty object oriented programming,
and is not optimal for interacting with the operating system. The
philosophy
is to let Fortran do what is best for, number crunching, and leave data
manipulation and file administration to external, powerful tools. Tools, like
awk, shell scripting, gnuplot, Perl and others, are quite powerful and
complement all the weaknesses of Fortran mentioned before. The plotting
program is chosen to be gnuplot, which provides very powerful tools to
manipulate the data and create massive and complicated plots. It can
also create publication quality plots and contribute to the “fun part” of
the learning experience by creating animations, interactive 3d plots etc.
All the tools used in the book are open source software and they are
accessible to everyone for free. They can be used in a Linux environment, but
they can also be installed and used in Microsoft Windows and Mac OS
X.
The other hard part in teaching computational physics to scientists and
engineers is to explain that the approach of solving a problem numerically is quite
different from solving it analytically. Usually, students of this level are coming
with a background in analysis and fundamental physics. It is hard to
put them into the mode of thinking about solving a problem using only
additions, multiplications and some logical operations. The hardest part is to
explain the discretization of a model defined analytically, which can be done
in many ways, depending on the accuracy of the approximation. Then,
one has to extrapolate the numerical solution, in order to obtain a good
approximation of the analytic one. This is done step by step in the book, starting
with problems in simple motion and ending with discussing finite size
scaling in statistical physics models in the vicinity of a continuous phase
transition.
The book comes together with additional material which can be found at the web page
of the book .
The accompanying software contains all the computer programs presented in the
book, together with useful tools and programs solving some of the exercises of
each chapter. Each chapter has problems complementing the material
covered in the text. The student needs to solve them in order to obtain
hands on experience in scientific computing. I hope that I have already
stressed enough that, in order for this book to be useful, it is not enough
to be read in a café or in a living room, but one needs to do what it
says.
Hoping that this book will be useful to you as a student or as an instructor, I
would like to ask you to take some time to send me feedback for improving and/or
correcting it. I would also appreciate fan mail or, if you are an expert, a review of
the book. If you use the book in a class, as a main textbook or as supplementary
material, I would also be thrilled to know about it. Send me email at
konstantmail.ntua.gr and let me know if I can publish, anonymously or not,
(part of) what you say on the web page (otherwise I will only use it privately
for my personal ego-boost). Well, nothing is given for free: As one of
my friends says, some people are payed in dollars and some others in
ego-dollars!
Have fun computing scientifically!
Athens, 2014.
Chapter 1
The Computer
The aim of this chapter is to lay the grounds for the development of the
computational skills which are necessary in the following chapters. It is not an in
depth exposition but a practical training by example. For a more systematic study
of the topics discussed, we refer to the bibliography. Many of the references are
freely available in the web.
The are many choices that one has to make when designing a computer
project. These depend on the needs for numerical efficiency, on available
programming hours, on the needs for extensibility and upgradability and so on. In
this book we will get the flavor of a project that is mostly scientifically and
number crunching oriented. One has to make the best of the available computing
resources and have powerful tools available for a productive analysis of the data.
Such an environment, found in most of today’s supercomputers, that offers
flexibility, dependability, simplicity, powerful tools for data analysis and effective
compilers is provided by the family of the Unix operating systems. The
GNU/Linux operating system is a Unix variant that is freely available
and most of its utilities are open source software. The voluntary work of
millions of excellent programmers worldwide has built the most stable,
fastest and highest quality software available for scientific computing today.
Thanks to the idea of the open source software pioneered by Richard
Stallman
this giant collaboration has been made possible.
Another choice that we have to make is the programming language, and this is
going to be Fortran. Fortran has been built mainly for numerical applications and
it has been used by many scientists and engineers because of its efficiency in high
performance computing. The language is simple and compilers are able to
optimize, parallelize and vectorize the code very efficiently. There is a lot of
scientific and engineering software available in libraries written in Fortran, which
has been used and tested extensively for many years. This is a crucial factor for
scientific software, so that it can be trusted to be efficient and free of errors.
Fortran is not the best choice for interacting with the operating system or for
text processing. This shortcoming can be easily overcome by the use of
external tools and Fortran can be left to do what she has been designed
for: number crunching. Its structure is simple and can be used both for
procedural and object oriented programming, in such a way that, it will not
make the life of an inexperienced programmer difficult, and at the same
time provide high level, abstract and powerful tools for high performance,
modular, object oriented, programming needed in a large and complicated
project.
Fortran, as well as other languages like C, C++ and Java, is a language that
needs to be compiled by a compiler. Other languages, like perl, awk, shell
scripting, Macsyma, Mathematica, Octave, Matlab,  , are interpreted
line by line. These languages can be simple in their use, but they can be
prohibitively slow when it comes to a numerically demanding program. A
compiler is a tool that analyzes the whole program and optimizes the
computer instructions executed by the computer. But if programming time is
more valuable, then a simple, interpreted language can lead to faster
results.
, are interpreted
line by line. These languages can be simple in their use, but they can be
prohibitively slow when it comes to a numerically demanding program. A
compiler is a tool that analyzes the whole program and optimizes the
computer instructions executed by the computer. But if programming time is
more valuable, then a simple, interpreted language can lead to faster
results.
Another choice that we make in this book, and we mention it because it is not the
default in most Linux distributions, is the choice of shell. The shell is a program that
“connects” the user to the operating system. In this book, we will teach how to use a
shell
to “send” commands to the operating system, which is the most effective way to
perform complicated tasks. We will use the shell tcsh, although most of the
commands can be interpreted by most popular shells. Shell scripting is simpler in
this shell, although shells like bash provide more powerful tools, mostly needed
for complicated system administration tasks. That may cause a small
inconvenience to some readers, since tcsh is not preinstalled in Linux
distributions .
1.1 The Operating System
The Unix family of operating systems offer an environment where complicated
tasks can be accomplished by combining many different tools, each of which
performs a distinct task. This way, one can use the power of each tool, so that
trivial but complicated parts of a calculation don’t have to be programmed. This
makes the life of a researcher much easier and much more productive, since
research requires from us to try many things before we understand how to
compute what we are looking for.
In the Unix operating system everything is a file, and files are organized in a
unique and unified filesystem. Documents, pictures, music, movies, executable
programs are files. But also directories or devices, like hard disks, monitors, mice,
sound cards etc, are, from the point of view of the operating system, files. In order
for a music file to be played by your computer, the music data needs to be written
to a device file, connected by the operating system to the sound card. The
characters you type in a terminal are read from a file “the keyboard”,
and written to a file “the monitor” in order to be displayed. Therefore,
the first thing that we need to understand is the structure of the Unix
filesystem.
1.1.1 Filesystem
There is at least one path in the filesystem associated with each file. There
are two types of paths, relative paths and absolute paths. These are two
examples:
bin/RungeKutta/rk.exe
/home/george/bin/RungeKutta/rk.exe
The paths shown above may refer to the same or a different file. This
depends on “where we are”. If “we are” in the directory /home/george,
then both paths refer to the same file. If on the other way “we are” in a
directory /home/john or /home/george/CompPhys, then the paths
refer
to two different files. In the last two cases, the paths refer to the files
/home/john/bin/RungeKutta/rk.exe
/home/george/CompPhys/bin/RungeKutta/rk.exe
respectively. How can we tell the difference? An absolute path always begins with
the / character, whereas a relative path does not. When we say that “we are in a
directory”, we refer to a position in the filesystem called the current directory, or
working directory. Every process in the operating system has a unique current
directory associated with it.
The filesystem is built on its root and looks like a tree positioned upside down.
The symbol of the root is the character / The root is a directory. Every directory
is a file that contains a list of files, and it is connected to a unique directory, its
parent directory . Its list of files contains other directories, called its subdirectories,
which all have it as their parent directory. All these files are the contents
of the directory. Therefore, the filesystem is a tree of directories with
the root directory at its top which branch to its subdirectories, which in
their turn branch into other subdirectories and so on. There is practically
no limit to how large this tree can become, even for a quite demanding
environment .
A path consists of a string of characters, with the characters / separating its
components, and refers to a unique location in the filesystem. Every component
refers to a file. All, but the last one, must be directories in a hierarchy, from
parent directory to subdirectory. The only exception is a possible / in the
beginning, which refers to the root directory. Such an example can be seen in
figure 1.1.
In a Unix filesystem there is complete freedom in the choice of the location of the
files .
Fortunately, there are some universally accepted conventions respected by almost
everyone. One expects to find home directories in the directory /home,
configuration files in the directory /etc, application executables in directories
with names such as /bin, /usr/bin, /usr/local/bin, software libraries in
directories with names such as /lib, /usr/lib etc.
There are some important conventions in the naming of the paths. A single
dot “.” refers to the current directory and a double dot “..” to the parent
directory. Similarly, a tilde “~” refers to the home directory of the user. Assume,
e.g., that we are the user george running a process with a current directory
/home/george/Music/Rock (see figure 1.1). Then, the following paths refer to the
same file /home/george/Doc/lyrics.doc:
../../Doc/lyrics.doc
~/Doc/lyrics.doc
~george/Doc/lyrics.doc
./../../Doc/lyrics.doc
Notice that ~ and ~george refer to the home directory of the user george
(ourselves), whereas ~mary refer to the home directory of another user,
mary.
We are now going to introduce the basic commands for filesystem navigation and
manipulation .
The command cd (=change directory) changes the current directory, whereas the
command pwd (=print working directory) prints the current directory:
> cd /usr/bin
> pwd
/usr/bin
> cd /usr/local/lib
> pwd
/usr/local/lib
> cd
> pwd
/home/george
> cd -
> pwd
/usr/local/lib
> cd ../../
> pwd
/usr
The argument of the command cd is an absolute or a relative path. If the path is
correct and we have the necessary permissions, the command changes the current
directory to this path. If no path is given, then the current directory changes to
the home directory of the user. If the character - is given instead of a path,
then the command changes the current directory to the previous current
directory.
The command mkdir creates new directories, whereas the command rmdir
removes empty directories. Try:
> mkdir new
> mkdir new/01
> mkdir new/01/02/03
mkdir: cannot create directory ‘new/01/02/03’: No such file or
directory
> mkdir -p new/01/02/03
> rmdir new
rmdir: ‘new’: Directory not empty
> rmdir new/01/02/03
> rmdir new/01/02
> rmdir new/01
> rmdir new
Note that the command mkdir cannot create directories more than one level
down the filesystem, whereas the command mkdir -p can. The “switch” -p makes
the behavior of the command different than the default one.
In order to list the contents of a directory, we use the command ls
(=list):
> ls
BE.eps Byz.eps Programs srBE_xyz.eps srB_xyz.eps
B.eps Bzy.eps srBd_xyz.eps srB_xy.eps
> ls Programs
Backup rk3_Byz.f90 rk3.f90
plot-commands rk3_Bz.f90 rk3_g.f90
The first command is given without an argument and it lists the contents of the
current directory. The second one, lists the contents of the subdirectory of the
current directory Programs. If the argument is a list of paths pointing to regular
files, then the command prints the names of the paths. Another way of giving the
command is
[literate={-}{{\texttt{-}}}1]%[basicstyle=\ttfamily]
> ls -l
total 252
-rw-r--r-- 1 george users 24284 May 1 12:08 BE.eps
-rw-r--r-- 1 george users 22024 May 1 11:53 B.eps
-rw-r--r-- 1 george users 29935 May 1 13:02 Byz.eps
-rw-r--r-- 1 george users 48708 May 1 12:41 Bzy.eps
drwxr-xr-x 4 george users 4096 May 1 23:38 Programs
-rw-r--r-- 1 george users 41224 May 1 22:56 srBd_xyz.eps
-rw-r--r-- 1 george users 23187 May 1 21:13 srBE_xyz.eps
-rw-r--r-- 1 george users 24610 May 1 20:29 srB_xy.eps
-rw-r--r-- 1 george users 23763 May 1 20:29 srB_xyz.eps
The switch -l makes ls to list the contents of the current directory together with
useful information on the files in 9 columns. The first column lists the permissions
of the files (see below). The second one lists the number of links of the
files .
The third one lists the user who is the owner of each file. The fourth one lists the
group that is assigned to the files. The fifth one lists the size of the file in bytes
(=8 bits). The next three ones list the modification time of the file and the last
one the paths of the files.
File permissions
are separated in three classes: owner permissions, group permissions and other
permissions. Each class is given three specific permissions, r=read, w=write and
x=execute. For regular files, read permission effectively means access to the file
for reading/copying, write permission means permission to modify the contents of
the file and execute permission means permission to execute the file as a
command .
For directories, read permission means that one is able to read the names of the
files in the directory (but not make it as current directory with the cd command),
write permission means to be able to modify its contents (i.e. create, delete, and
rename files) and execute permission grants permission to access/modify the
contents of the files (but not list the names of the files, this is granted by the read
permission).
The command ls -l lists permissions in three groups. The owner (positions
2-4), the group (positions 5-7) and the rest of the world (others - positions 8-10).
For example
[literate={-}{{\texttt{-}}}1]
-rw-r--r--
-rwxr-----
drwx--x--x
In the first case, the owner has read and write but not execute permissions and
the group+others have only read permissions. In the second case, the user has
read, write and execute permissions, the group has read permissions and others
have no permissions at all. In the last case, the user has read, write and execute
permissions, whereas the group and the world have only execute permissions. The
first character d indicates a special file, which in this case is a directory. All
special files have this position set to a character, while regular files have it set to
-.
File permissions can be modified by using the command chmod:
> chmod u+x file
> chmod og-w file1 file2
> chmod a+r file
Using the first command, the owner (u user) obtains (+) permission to
execute (x) the file named file. Using the second one, the rest of the world (o
user) obtains (+) permission to
execute (x) the file named file. Using the second one, the rest of the world (o others) and the group (g
others) and the group (g group) loose (-) the write (w) permission to the files
named file1 and file2. Using the third one, everyone (a
group) loose (-) the write (w) permission to the files
named file1 and file2. Using the third one, everyone (a all) obtain read (r)
permission on the file named file.
all) obtain read (r)
permission on the file named file.
We will close this section by discussing some commands which are used for
administering files in the filesystem. The command cp (copy) copies the contents
of files into other files:
> cp file1.f90 file2.f90
> cp file1.f90 file2.f90 file3.f90 Programs
If the file file2.f90 does not exist, the first command copies the contents of
file1.f90 to a new file file2.f90. If it already exists, it replaces its
contents by the contents of the file file2.f90. In order for the second
command to be executed, Programs needs to be a directory. Then, the
contents of the files file1.f90, file2.f90, file3.f90 are copied to
indentical files in the directory Programs. Of course, we assume that
the user has the appropriate privileges for the command to be executed
successfully.
The command mv “moves”, or renames, files:
> mv file1.f90 file2.f90
> mv file1.f90 file2.f90 file3.f90 Programs
The first command renames the file file1.f90 to file2.f90. The second
one moves files file1.f90, file2.f90, file3.f90 into the directory
Programs.
The command rm (remove) deletes
files .
Beware, the command is unforgiving: after deletion, a file cannot be restored into the
filesystem .
Therefore, after executing successfully the following commands
> ls
file1.f90 file2.f90 file3.f90 file4.csh
> rm file1.f90 file2.f90 file3.f90
> ls
file4.csh
the files file1.f90, file2.f90, file3.f90 do not exist in the filesystem
anymore. A more prudent use of the command demands the flag -i. Then, before
deletion we are asked for confirmation:
> rm -i *
rm: remove regular file ‘file1.f90’? y
rm: remove regular file ‘file2.f90’? y
rm: remove regular file ‘file3.f90’? y
rm: remove regular file ‘file4.csh’? n
> ls
file4.csh
When we type y, the file is deleted, when we type n, the file is not deleted.
We cannot remove directories the same way. It is possible to use the command
rmdir in order to remove empty directories. In order to delete directories together
with their contents (including subdirectories and their contents) use the
command
rm -r. For example, assume that the contents of the directories dir1 and
dir1/dir2 are the files:
./dir1
./dir1/file2.f90
./dir1/file1.f90
./dir1/dir2
./dir1/dir2/file3.f90
Then the results of the following commands are:
> rm dir1
rm: cannot remove ‘dir1’: Is a directory
> rm dir1/dir2
rm: cannot remove ‘dir1/dir2’: Is a directory
> rmdir dir1
rmdir: dir1: Directory not empty
> rmdir dir1/dir2
rmdir: dir1/dir2: Directory not empty
> rm -r dir1
The last command removes all files (assuming that we have write permissions
for all directories and subdirectories). Alternatively, we can empty the
contents of all directories first, and then remove them with the command
rmdir:
> cd dir1/dir2; rm file3.f90
> cd .. ; rmdir dir2
> rm file1.f90 file2.f90
> cd .. ; rmdir dir1
Note that by using a semicolon, we can execute two or more commands on the
same line.
1.1.2 Commands
Commands in a Unix operating system are files with execute permission. When
we write a sentence on the command line, like
> ls -l test.f90 test.dat
the shell reads its and interprets it. The shell is a program that creates a interface
between a user and the operating system. The first word (ls) of the sentence is
interpreted as a command. The rest of the words are the arguments of the
command and the program can use them (or not) at the discretion of its
programmer. There is a special convention for arguments that begin with a - (e.g.
-l, --help, --version, -O3). They are called options or switches, and they act as
virtual switches that make the program act in a particular way. We have
already seen that the program ls gives a different output with the switch
-l.
In order for a command to be executed, the shell looks for a file that has the
same name as the command (here a file named ls). In order to understand where
the shell looks for such a file, we should digress a little bit and explain the use
of shell variables and environment variables. These have a name, which
is a string of permissible characters, and their values are obtained by
preceding their name with the $ character. For example the variable PATH has
value $PATH. The values of the environment variables can be set with the
command
setenv and of the shell variables with the command set:
> setenv MYVAR test-env
> set myvar = test-shell
> echo $MYVAR $myvar
test-env test-shell
Two special variables are the variables PATH and path:
>echo $PATH
/usr/local/bin:/usr/bin:/bin:/usr/X11/bin
>echo $path
/usr/local/bin /usr/bin /bin /usr/X11/bin
The first one is an environment variable and the second one is a shell variable.
Their values are set by the shell, and we don’t need to worry about them, unless
we want to change them. Their value is a string of characters whose components
should be valid paths to directories. In the first case, the components are
separated by a :, while in the second case, by one or more spaces. In the
example shown above, the shell searches each component of the path or
PATH variables (in this order) until it finds a file ls in their contents. If
it succeeds and the file has execute permissions, then the program in
this file is executed. If it fails, then it prints an error message. Try the
commands:
> which ls
/bin/ls
> ls -l /bin/ls
-rwxr-xr-x 1 root root 93560 Sep 28 2006 /bin/ls
We see that the program that the ls command executes the program in the file
/bin/ls.
The arguments of a command are passed on to the program that the command
executes for possible interpretation. For example:
> ls -l test.f90 test.dat
The argument -l is the switch that results in a long listing of the files. The
arguments test.f90 and test.dat are interpreted by the program ls as paths
that it will look up for file information.
You can use the * (wildcard) character as a shorthand notation for a group of
files. For example, in the command shown below
> ls -l *.f90 *.dat
the shell will expand *.f90 and *.dat to a list of all files whose names end with
.f90 or .dat. Therefore, if the current directory contains the files test.f90,
test1.f90, myprog.f90, test.dat, hello.dat, the arguments that will be
passed on to the command ls are
> ls -l myprog.f90 test1.f90 test.f90 hello.dat test.dat
For each command there are three special files associated with it. The first
one is the standard input (stdin), the second one is the standard output
(stdout) and the third one the standard error (stderr). These are files
where the program can print or read data from. By default, these files are
the terminal that the user uses to execute the command. In this case,
when the program reads data from the stdin, then it reads the data that
we type to the terminal using the keyboard. When the program writes
data to the stdout or to the stderr, then the data is written to the
terminal.
The advantage of using these special files in order to read/write data is that
the user can redirect the input/output to these files to any file she wants. Using
the character > at the end of a command redirects the stdout to the file whose
name is written after >. For example:
> ls
file1.f90 file2.f90 file3.f90 file4.csh
> ls > results
> ls
file1.f90 file2.f90 file3.f90 file4.csh results
The first of the above commands, prints the contents of the current working
directory to the terminal. The second command redirects data written to
the stdout to the file results. After executing the command, the file
results is created and its contents are the names of the files file1.f90
file2.f90 file3.f90 file4.csh. If the file results does not exist
(as in the above example), the file is created. If it already exists, it is
truncated and its contents replaced by the data written to the stdout of the
command. If we want to append data without erasing the existing contents,
then we should use the string of characters >>. Therefore, if we give the
command
> ls >> results
after executing the previous commands, then the contents of the file results will
be
file1.f90 file2.f90 file3.f90 file4.csh
file1.f90 file2.f90 file3.f90 file4.csh results
The redirection of the stdin is accomplished by the use of the
character < while that of the stderr by the use of the string of
characters
>&. We will see more examples in section 1.2.
It is possible to redirect the stdout of a command to be the stdin of
another command. This is very useful for creating filters. A filter is a
command that creates a flow of data between two or more programs.
This process is called piping. Pipes are creating by using the character
|
> cmd1 | cmd2 | cmd3 | ... | cmdN
Using the syntax shown above, the stdout of the command cmd1 is redirected to
the stdin of the command cmd2, the stdout of the command cmd2 is redirected
to the stdin of the command cmd3 etc. More examples will be presented in
section 1.2.
1.1.3 Looking for Help
Unix got itself a reputation for not being user friendly. This is far from the truth.
Although there is a steep learning curve, detailed documentation for almost
everything is available online.
The key for a comfortable ride is to learn how to use the help system available
on your computer and on the internet. Most of the commands are self
documented. A simple test, like the one shown below, will help you with the basic
usage of most of the commands:
[literate={-}{{\texttt{-}}}1]
> cmd --help
> cmd -h
> cmd -help
> cmd -\?
For example, try the command ls --help. For a window application, start from
the menu “Help”. You should not be afraid and/or lazy and you should proceed
with careful searching and reading.
For example, let’s assume that you have heard about a command that sounds
like printf, or something like that. The first level of online help is the man
(=manual) command that searches the “man pages”. Read the output of the
command
> man printf
The command info usually provides more detailed and user friendly
documentation. It has basic browsing capabilities like the browsers you use to
read pages from the internet. Try the command
> info printf
Furthermore, the commands
> man -k printf
> whatis printf
will inform you that there are other, possibly related, commands with names like
fprintf, fwprintf, wprintf, sprintf...:
> whatis printf
printf (1) - format and print data
printf (1p) - write formatted output
printf (3) - formatted output conversion
printf (3p) - print formatted output
printf [builtins] (1) - bash built-in commands, see bash(1)
The second column printed by the whatis command is the “section” of the man
pages. In order to gain access to the information in a particular section, you have
to give it as an argument to the man command:
> man 1 printf
> man 1p printf
> man 3 printf
> man 3p printf
> man bash
Section 1 of the man pages contains information of ordinary command line
commands, section 3 contains information on functions in libraries of
the C language. Section 2 contains information on commands used for
system administration. You may browse the directory /usr/share/man, or
read the man page of the man command (use the command man man for
that!).
By using the command
[literate={-}{{\texttt{-}}}1]
> printf --help
we obtain plenty of memory refreshing information. The command
> locate printf
shows us many files related to the command printf. The commands
> which printf
> where printf
give information on the location of the executable(s) of the command
printf.
Another useful feature of the shell is the command or it filename completion.
This means that we can write only the first characters of the name
of a command or filename and then press simultaneously the keys
[Ctrl-d]
(i.e. press the key Ctrl and the key of the letter d at the same time). Then the shell will
complete the name of the command up to the point that is is unique with the given string of
characters :
> pri[Ctrl-d]
printafm printf printenv printnodetest
Try to type an x on the command line and then type [Ctrl-d]. You will learn all
the commands that are available and whose name begins with an x: xterm,
xeyes, xclock, xcalc, ...
Finally, the internet contains a wealth of information. Google your blues... and
you will be rewarded!
1.2 Text Processing Tools – Filters
For doing data analysis, we will need powerful tools for manipulating data in text
files. These are files that consist solely of printable characters. Some tools that can
be used in order to construct complicated and powerful filters are the programs
cat, less, head, tail, grep, sort and awk.
Suppose that we have data in a file named
data
which contains information on the contents of a food warehouse and their
prices:
bananas 100 pieces 1.45
apples 325 boxes 1.18
pears 34 kilos 2.46
bread 62 kilos 0.60
ham 85 kilos 3.56
The command
> cat data
prints the contents of the file data to the stdout. In general, this command
prints the contents of all files given in its arguments or the stdin if none is given.
Since the stdin and the stdout can be redirected, the command
> cat < data > data1
takes the contents of the file data from the stdin and prints them to the stdout,
which in this case is the file data1. This command has the same result as the
command:
> cp data data1
The command
> cat data data1 > data2
prints the contents of the file data and then the contents of the file data1 to the
stdout. Since the stdout is redirected to the file data2, data2 contains the data
of both files.
By giving the command
> less gfortran.txt
you can browse the data contained in the file gfortran.txt one page at a time.
Press [space] in order to “turn” a page, [b] to turn back a page. Press the up
and down arrows to move one line backwards/forward. Press [g] in order to
jump to the beginning of the file and press [G] in order to jump to the
end. Press [h] in order to get a help message and press [q] in order to
quit.
The commands
> head -n 1 data
bananas 100 pieces 1.45
> tail -n 2 data
bread 62 kilos 0.60
ham 85 kilos 3.56
> tail -n 2 data | head -n 1
bread 62 kilos 0.60
print the first line, the last two lines and the second to the last line of the file
data to the stdout respectively. Note that, by piping the stdout of the command
tail to the stdin of the command head, we are able to construct the filter “print
the line before the last one”.
The command sort sorts the contents of a file by comparing each line of its
text with all others. The sorting is alphabetical, unless otherwise set by using
options. For example
> sort data
apples 325 boxes 1.18
bananas 100 pieces 1.45
bread 62 kilos 0.60
ham 85 kilos 3.56
pears 34 kilos 2.46
For reverse sorting, try sort -r data. We can also sort by comparing specific
fields of each line. By default, fields are words separated by one or more spaces.
For example, in order to sort w.r.t. the second column of the file data, we can use
the switch -k 2 (=second field). Furthermore, we can use the switch -n for
numerical sorting:
> sort -k 2 -n data
pears 34 kilos 2.46
bread 62 kilos 0.60
ham 85 kilos 3.56
bananas 100 pieces 1.45
apples 325 boxes 1.18
If we omit the switch -n, the comparison of the lines is performed based on
character sorting of the second field and the result is
> sort -k 2 data
bananas 100 pieces 1.45
apples 325 boxes 1.18
pears 34 kilos 2.46
bread 62 kilos 0.60
ham 85 kilos 3.56
The last column contains floating point numbers (not integers). In order to sort
by the values of such numbers we should use the switch -g:
> sort -k 4 -g data
bread 62 kilos 0.60
apples 325 boxes 1.18
bananas 100 pieces 1.45
pears 34 kilos 2.46
ham 85 kilos 3.56
The command grep processes a text file line by line, searching for a given
string of characters. When this string is found anywhere in a line, this line is
printed to the stdout. The command
> grep kilos data
pears 34 kilos 2.46
bread 62 kilos 0.60
ham 85 kilos 3.56
prints each line containing the string “kilos”. If we want to search for all line not
containing the string “kilos”, then we add the switch -v:
> grep -v kilos data
bananas 100 pieces 1.45
apples 325 boxes 1.18
We can use a regular expression for searching a whole family of strings of
characters. These monsters need a full book for discussing them in detail! But it is
not hard to learn how to use some simple forms of regular expressions. Here are
some examples:
> grep ^b data
bananas 100 pieces 1.45
bread 62 kilos 0.60
> grep ’0$’ data
bread 62 kilos 0.60
> grep ’3[24]’ data
apples 325 boxes 1.18
pears 34 kilos 2.46
The first one, prints each line whose first character is a b. The second one, prints
each line that ends with a 0. The third one, prints each line contaning the strings
32 or 34.
By far, the strongest tool in our toolbox is the awk program. By default, awk
analyzes a text file line by line. Each word (or field in the awk jargon) of these
lines is stored in a set of variables with names $1, $2, .... The variable $0
contains the full line currently processed, whereas the variable NF counts the
number of fields in the current line. The variable NR counts the number of lines of
the file processed so far by awk.
An awk program can be written in the command line. A set of commands
within { ... } is executed for each line of input. The constructs BEGIN{ ... }
and END{ ... } contain commands executed, only once, before and after the
processing of the file respectively. For example, the command
> awk ’{print $1,"total value= ",$2*$4}’ data
bananas total value= 145
apples total value= 383.5
pears total value= 83.64
bread total value= 37.2
ham total value= 302.6
prints the name of the product (1st column = $1) and the total value stored in
the warehouse (2nd column = $2)  (4th column = $4). More examples are
given below:
(4th column = $4). More examples are
given below:
> awk ’{value += $2*$4}END{print "Total= ",value}’ data
Total= 951.94
> awk ’{av += $4}END{print "Average Price= ",av/NR}’ data
Average Price= 1.85
> awk ’{print $2^2 * sin($4) + exp($4)}’ data
The first one calculates the total value of all products: The processing of each line
results in the increment (+=) of the variable value by the product of the second
and fourth fields. In the end (END{ ... }), the string Total= is printed, together
with the final value of the variable value. This is an easy way for computing
the sum of the values calculated for each line. The second command,
calculates and prints an average. The sum is calculated in each line and stored
in the variable av. In the end, we print the quotient of the sum of all
values by the number of lines that have been processed (NR). The last
command shows a (crazy) mathematical expression based on numerical values
found in each line of the file data: It computes the square of the second
field times the sine of the fourth field plus the exponential of the fourth
field.
There is much more potential in the commands presented above. Reading the
documentation and getting experience by using them will provide you with very
strong tools in order to accomplish complicated tasks.
1.3 Programming with Emacs
For a programmer that spends many hours programming every day, the
environment and the tools available for editing the commands of a large and
complicated program determine, to a large extent, the quality of her life! An
editor edits the contents of a text file, that consists solely of printable characters.
Such editors, available in most Linux environments, are the programs gedit,
vim, pico, nano, zile... They provide basic functionality such as adding,
removing or changing text within a file as well as more complicated functions,
such as copying, pasting, searching and replacing text etc. There are many
functions that are particularly useful to a programmer, such as detecting and
formatting keywords of a particular programming language, pretty printing,
closing scopes etc, which can be very useful for comfortable programming and for
spotting errors. A very powerful and “knowledgeable” editor, offering many
such functions for several programming languages, is the GNU Emacs
editor .
Emacs is open source software, it is available for free and
can be used in most available operating systems. It is
programmable
and the user can automate most of her everyday repeated tasks and configure it to
her liking. There is a full interaction with the operating system, in fact Emacs has
been built with the ambition of becoming an operating system. For example, a
programmer can edit a Fortran file, compile it, debug it and run it, everything
done with Emacs commands.
1.3.1 Calling Emacs
In the command line type
> emacs &
Note the character & at the end of the line. This makes the particular command
to run in the background. Without it, the shell waits until a command exits in
order to return the prompt.
In a desktop environment, Emacs starts in its own window. For a quick and
dirty editing session, or in the case that a windows environment is not
available ,
we can run Emacs in a terminal mode. Then, we omit the & at the end of the line
and we run the command
> emacs -nw
The switch -nw forces Emacs to run in terminal mode.
1.3.2 Interacting with Emacs
We can interact with Emacs in various ways. Newbies will prefer buttons and
menus that offer a simple and intuitive interface. For advanced usage, however, we
recommend that you make an effort to learn the keyboard shortcuts. There are
also thousands of functions available to be used interactively. They are
called from a “command line”, called the minibuffer in the Emacs jargon.
Keyboard shortcuts are usually combinations of keystrokes that
consist of the simultaneous pressing of the Ctrl or Alt keys together
with other keys. Our convention is that a key sequence starting with a C-
means that the characters that follow are keys simultaneously pressed
with the Ctrl key. A key sequance starting with a M- means that the
characters that follow are keys simultaneously pressed with the Alt
key .
Some commands have shortcuts consisting of two or more composite keystrokes.
For example by C-x C-c we mean that we have to press simultaneously the Ctrl
key together with x and then press simultaneously the Ctrl key together with c.
This sequence is a shortcut to the command that exits Emacs. Another example is
C-x 2 which means to press the Ctrl key together with x and then press only the
key 2. This is a shortcut to the command that splits a window horizontally to two
equal parts.
The most useful shortcuts are M-x (press the Alt key siumutaneously with the
x key) and C-g. The first command takes us to the minibuffer where we can
give a command by typing its name. For example, type M-x and then
type save-buffers-kill-emacs in the minibuffer (this will terminate
Emacs). The second one is an “SOS button” that interrupts anything Emacs
does and returns control to the working buffer. This can be pretty handy
when a command hangs or destroys our work and we need to interrupt
it.
The conventions for the mouse events are as follows: With Mouse-1, Mouse-2
and Mouse-3 we denote a simple click with the left, middle and right buttons of
the mouse respectively. With Drag-Mouse-1 we mean to press the left button of
the mouse and at the same time drag the mouse.
We summarize the possible ways of giving a command in Emacs with the
following examples that have the same effect: Open a file and put its contents in a
buffer for editing.
- By pressing the toolbar button that looks like a white sheet of paper
(see figure 1.2).
- By choosing the File
 Visit New File menu entry.
Visit New File menu entry.
- By typing the keyboard shortcut C-x C-f.
- By typing the name of the command in the minibuffer: M-x find-file
The number of available commands increases from the top to the bottom of the above
list.
1.3.3 Basic Editing
In order to edit a file, Emacs places the contents of a file in a buffer. Such a buffer
is a chunk of computer memory where the contents of the file are copied and it is
not the file itself. When we make changes to the contents of a buffer, the file
remains intact. For our changes to take effect and be written to the file, we
have to save the buffer. Then, the contents of the buffer are written back
to the file. It is important to understand the following cycle of events:
- Read a file’s contents to a buffer.
- Edit buffer contents.
- Write (save) buffer’s contents back into the file.
Emacs may have more than one buffers open for editing simultaneously. By default, the
name of the buffer is the same as the name of the file that is edited, although this is not
necessary .
The name of a buffer is written in the modeline of the window of the buffer, as
can be seen in figure 1.3.
If Emacs crashes or exits before we save our edits, it is possible to recover
(part of) them. There is a command M-x recover-file that will guide us
through the necessary recovery steps, or we can look for a file that has the same
name as the buffer we were editing surrounded by two #. For example, if we were
editing the file file.f90, the automatically saved changes can be found in the file
#file.f90#. Auto saving is done periodically by Emacs and its frequency can be
controlled by the user.
The point where we insert text while editing is called “the point”. This is right before the
blinking cursor .
Each buffer has another position marked by “the mark”. A point and the
mark define a “region” in the buffer. This is a part of the text in the
buffer where the functions of Emacs can act (e.g. copy, cut, change case,
spelling etc.). We can set the region by setting a point and then press
C-SPC
or give the command M-x set-mark-command. This defines the current point to
be the mark. Then we can move the cursor to another point which will define
a region together with the mark that we set. Alternatively we can use
Drag-Mouse-1 (hold the left mouse button and drag the mouse) and
mark a region. The mark can be set with Mouse-3, i.e. with a simple click
of the right button of the mouse. Therefore by Mouse-1 at a point and
then Mouse-3 at a different point will set the region between the two
points.
We can open a file in a buffer with the command C-x C-f, and then by typing
its path. If the file already exists, its contents are copied to a buffer, otherwise a
new buffer is created. Then:
- We can browse the buffer’s contents with the Up/Down/Left/Right
arrows. Alternatively, by using the commands C-n, C-p, C-f and C-b.
- If the buffer is large, we can browse its contents one page at a
time by using the Page Up/Page Dn keys. Alternatively, by using the
commands C-v, M-v.
- Enter text at the points simply by typing it.
- Delete characters before the point by using the Backspace key and
after the point by using the Delete key. The command C-d deletes a
forward character.
- Erase all the characters in a line that lie ahead of the point by using
the command C-k.
- Open a new line by using Enter or C-o.
- Go to the first character of a line by using Home and the last one by using
End. Alternatively, by using the commands C-a and C-e, respectively.
- Go to the first character of the buffer with the key C-Home
and the last one with the key C-End. Alternatively, with M-x
beginning-of-buffer and M-x end-of-buffer.
- Jump to any line we want: Type M-x goto-line and then the line
number.
- Search for text after the point: Press C-s and then the text you
are looking for. This is an incremental search and the point jumps
immediately to the first string that matches the search. The same search
can be repeated by pressing C-s repeatedely.
When we finish editing (or frequently enough so that we don’t loose our work
due to an unfortunate event), we save the changes in the buffer, either by pressing
the save icon on the toolbar, or by pressing the keys C-s, or by giving the
command M-x save-buffer.
1.3.4 Cut and Paste
Use the instructions below for slightly more advanced editing:
- Undo! Some of the changes described below can be catastrophic. Emacs
has a great Undo function that keeps in its memory many of the changes
inflicted by our editing commands. By repeatedely pressing C-/, we
undo the changes we made. Alternatively, we can use C-x u or the
menu entry Edit
 Undo. Remember that C-g interrupts any Emacs
process currently running in the buffer.
Undo. Remember that C-g interrupts any Emacs
process currently running in the buffer.
- Cut text by using the mouse: Click with Mouse-1 at the point before
the beginning of the text and then Mouse-3 at the point after the end.
A second Mouse-3 and the region is ... gone (in fact it is written in the
“kill ring” and it is available for pasting)!
- Cut text by using a keyboard shortcut: Set the mark by C-SPC at the
point before the beginning of the text that you want to cut. Then move
the cursor after the last character of the text that you want to cut and
type C-w.
- Copy text by using the mouse: Drag the mouse Drag-Mouse-1 and
mark the region that you want to copy. Alternatively, Mouse-1 at the
point before the beginning of the text and then Mouse-3 at the point
after the end.
- Copy text by using a keyboard shortcut: Set the mark at the beginning
of the text with C-SPC and then move the cursor after the last character
of the text. Then type M-w.
- Pasting text with the mouse: We click the middle button
Mouse-2 at the point that we want to insert the text from the kill ring
(the copied text).
- Pasting text with a keyboard shortcut: We move the point to the desired
insertion point and type C-y.
- Pasting text from previous copying: A fast choice is the menu entry
Edit
 Paste from kill manu and then select from the copied
texts. The keyboard shortcut is to first type C-y and then M-y
repeatedly, until the text that we want is yanked.
Paste from kill manu and then select from the copied
texts. The keyboard shortcut is to first type C-y and then M-y
repeatedly, until the text that we want is yanked.
- Insert the contents of a file: Move the point to the desired place and
type C-x i and the path of the file. Alternatively, give the command
M-x insert-file.
- Insert the contents of a buffer: We can insert the contents of a whole
buffer at a point by giving the command M-x insert-buffer.
- Replace text: We can replace text interactively with the command M-x
query-replace, then type the string we want to replace, and then the
replacement string. Then, we will be asked whether we want the change
to be made and we can answer by typing y (yes), n (no), q (quit the
replacements). A , (comma) makes only one replacement and quits
(useful if we know that this is the last change that we want to make).
If we are confident, we can change all string in a buffer, no questions
asked, by giving the command M-x replace-string.
- Change case: We can change the case in the words of a region with
the commands M-x upcase-region, M-x capitalize-region and M-x
downcase-region. Try it.
We note that cutting and pasting can be made between different windows of the same
or different buffers.
1.3.5 Windows
Sometimes it is very convenient to edit one or more different buffers in two or
more windows. The term “windows” in Emacs refers to regions of the same Emacs
desktop window. In fact, a desktop window running an Emacs session is referred
to as a frame in the Emacs jargon. Emacs can split a frame in two or
more windows, horizontally or/and vertically. Study figure 1.5 on page
81 for details. We can also open a new frame and edit several buffers
simultaneously .
We can manipulate windows and frames as follows:
- Position the point at the center of the window and clear the screen
from garbage: C-l (careful: l not 1).
- Split a window in two, horizontally: C-x 2.
- Split a window in two, vertically: C-x 3.
- Delete all other windows (remain only with the current one): C-x 1.
- Delete the current windows (the others remain): C-x 0.
- Move the cursor to the other window: Mouse-1 or C-x o.
- Change the size of window: Use Drag-Mouse-1 on the line separating
two windows (the mode line). Use C-^, C-} for making a change of the
horizontal/vertical size of a window respectively.
- Create a new frame: C-x 5 2.
- Delete a frame: C-x 5 0.
- Move the cursor to a different frame: With Mouse-1 or with C-x 5 o.
You can have many windows in a dumb terminal. This is a blessing when a dekstop
environment is not available. Of course, in that case you cannot have many
frames.
1.3.6 Files and Buffers
- Open a file: C-x C-f or M-x find-file.
- Save a buffer: C-x C-s or M-x save buffer. With C-x C-c or M-x
save-buffers-kill-emacs we can also exit Emacs. From the menu:
File
 Save. From the toolbar: click on the save icon.
Save. From the toolbar: click on the save icon.
- Save buffer contents to a different file: C-x C-w or M-x write-file.
From the menu: File
 Save As. From the toolbar: click on the
“save as” icon.
Save As. From the toolbar: click on the
“save as” icon.
- Save all buffers: C-x s or M-x save-some-buffers.
- Connect a buffer to a different file: M-x set-visited-filename.
- Kill a buffer: C-x k.
- Change the buffer of the current window: C-x b. Also, use the menu
Buffers, then choose the name of the buffer.
- Show the list of all buffers: C-x C-b. From the menu: Buffers
 List All Buffers. By typing Enter next to the name of the buffer, we
make it appear in the window. There are several buffer administration
commands. Learn about them by typing C-h m when the cursor is in
the Bufer List window.
List All Buffers. By typing Enter next to the name of the buffer, we
make it appear in the window. There are several buffer administration
commands. Learn about them by typing C-h m when the cursor is in
the Bufer List window.
- Recover data from an edited buffer: If Emacs crashed, do not despair.
Start a new Emacs and type M-x recover-file and follow the
instructions. The command M-x recover-session recovers all unsaved
buffers.
- Backup files: When you save a buffer, the previous contents of the file
become a backup file. This is a file whose path is the same as the
original’s file with a ~ appended in the end. For example a file test.f90
will have as a backup the file test.f90~. Emacs has version control,
and you can configure it to keep as many versions of your edits as you
want.
- Directory browsing and directory administration commands: C-x d or
M-x dired. You can act on the files of a directory (open, delete, rename,
copy etc) by giving appropriate commands. When the cursor is in the
dired window, type C-h m to read the relevant documentation.
1.3.7 Modes
Each buffer can be in different modes. Each mode may activate different
commands or editing environment. For example each mode can color keywords
relevant to the mode and/or bind keys to different commands. There
exist major modes, and a buffer can be in only one of them. There are
also minor modes, and a buffer can be in one or more of them. Emacs
activates major and minor modes by default for each file. This usually
depends on the filename but there are also other ways to control this. The
user can change both major and minor modes at will, using appropriate
commands.
Active modes are shown in a parenthesis on the mode line (see figures 1.3 and
1.5.
- M-x f90-mode: This mode is of special interest in this book since we will
edit a lot of Fortran code. We need it activated in buffers that contain a
Fortran program and its most useful characteristics are automatic code
alignment by pressing the key TAB, the coloring of Fortran commands,
variables and other structural constructs (subroutines, if statements, do
loops, variable declarations, statement labels etc). Another interesting
function is the one that comments out a whole region of code, as well
as the inverse function.
- M-x c-mode: For files containing programs written in the C
language. Related modes are the c++-mode, java-mode, perl-mode,
awk-mode, python-mode, makefile-mode, octave-mode,
gnuplot-mode, mathematica-mode and others.
- latex-mode: For files containing LATEX text formatting commands.
- text-mode: For editing simple text files (.txt).
- fundamental-mode: The basic mode, when one that fits better doesn’t
exist...
Some interesting minor modes are:
- M-x auto-fill-mode: When a line becomes too long, it is wrapped
automatically. A related command to do that for the whole region is
M-x fill-region, and for a paragraph M-x fill-paragraph.
- M-x overwite-mode: Instead of inserting characters at the point,
overwrite the existing ones. By giving the command several times, we
toggle between activating and deactivating the mode.
- M-x read-only mode: When visiting a file with valuable data that
we don’t want to change by mistake, we can activate this mode so
that changes will not be allowed by Emacs. When we open a file with
the command C-x C-r or M-x find-file-read-only this mode is
activated. We can toggle this mode on and off with the command C-x
C-q (M-x toggle-read-only). See the mode line of the buffer jack.c
in figure 1.5 which contains a string %%. By clicking on the %% we can
toggle the read-only mode on and off.
- flyspell-mode: Spell checking as we type.
- font-lock-mode: Colors the structural elements of the buffer which are
defined by the major mode (e.g. the commands of a Fortran program).
In a desktop environment, we can choose modes from the menu of the mode
line. By clicking with Mouse-3 on the name of a mode we are offered options
for (de)activating minor modes. With a Mouse-1 we can (de)activate
the read-only mode with a click on :%% or :-- respectively. See figure
1.5.
1.3.8 Emacs Help
Emacs’ documentation is impressive. For newbies, we recommend to follow the
mini course offered by the Emacs tutorial. You can start the tutorial by typing
C-h t or select Help  Emacs Tutorial from the menu. Enjoy... The Emacs
man page (give the man emacs command in the command line) will give you a
summary of the basic options when calling Emacs from the command
line.
Emacs Tutorial from the menu. Enjoy... The Emacs
man page (give the man emacs command in the command line) will give you a
summary of the basic options when calling Emacs from the command
line.
A quite detailed manual can be found in the Emacs info
pages .
Using info needs some training, but using the Emacs interface is quite intuitive
and similar to using a web browser. Type the command C-h r (or choose
Help Emacs Tutorial from the menu) and you will open the front page of
the emacs manual in a new window. By using the keys SPC and Backspace we can
read the documentation page by page. When you find a link (similar to web page
hyperlinks), you can click on it in order to open to read the topic it refers to.
Using the navigation icons on the toolbar, you can go to the previous or to
the next pages, go up one level etc. There are commands that can be
given by typing single characters. For example, type d in order to jump to
the main info directory. There you can find all the available manuals in
the info system installed on your computer. Type g (emacs) and go to
the top page of the Emacs manual. Type g (info) and read the info
manual.
Emacs Tutorial from the menu) and you will open the front page of
the emacs manual in a new window. By using the keys SPC and Backspace we can
read the documentation page by page. When you find a link (similar to web page
hyperlinks), you can click on it in order to open to read the topic it refers to.
Using the navigation icons on the toolbar, you can go to the previous or to
the next pages, go up one level etc. There are commands that can be
given by typing single characters. For example, type d in order to jump to
the main info directory. There you can find all the available manuals in
the info system installed on your computer. Type g (emacs) and go to
the top page of the Emacs manual. Type g (info) and read the info
manual.
Emacs is structured in an intuitive and user friendly way. You will learn a lot
from the names of the commands: Almost all names of Emacs commands consist
of whole words, separated by a hyphen “-”, which almost form a full sentence.
These make them quite long sometimes, but by using auto completion of their
names this does not pose a grave problem.
- auto completion: The names of the commands are auto completed
by typing a TAB one or more times. E.g., type M-x in order to go
to the minibuffer. Type capi[TAB] and the command autocompletes
to capitalize-. By typing [TAB] for a second time, a new window
opens and offers the options for completing to two possible commands:
capitalize-region and capitalize-word. Type an extra r[TAB]
and the command auto completes to the only possible choice
capitalize-region. You can see all the commands that start with
an s by typing M-x s[TAB][TAB]. Sure, there are many... Click on the
*Completions* buffer and browse the possibilities. A lot will become
clear just by reading the names of the commands. By typing M-x
[TAB][TAB], all available commands will appear in your buffer!
- keyboard shortcuts: If you don’t remember what happens when you
type C-s, no problem: Type C-h k and then the ... forgotten key
sequence C-s. Conversely, have you forgotten what is the keyboard
shortcut of the command save-buffer? Type C-h w and then the
command.
- functions: Are you looking for a command, e.g. save-something
-I-forgot? Type C-h f and then save-[TAB] in order to browse over
different choices. Use Mouse-2 in order to select the command you are
interested in, or type and complete the rest of its name (you may use
[TAB] again). Read about the function in the *Help* buffer that opens.
- variables: Do the same after typing C-h v in order to see a variable’s
value and documentation.
- command apropos: Have you forgotten the exact name of a command?
No problem... Type C-h a and a keyword. All commands related to the
keyword you typed will appear in a buffer. Use C-h d for even more
information.
- modes: When in a buffer, type C-h m and read information about the
active modes of the buffer.
- info: Type C-h i
- Have you forgotten everything mentioned above? Just type C-h ?
1.3.9 Emacs Customization
You can customize everything in Emacs. From key bindings to programming your
own functions in the Elisp language. The most common way for a user to
customize her Emacs sessions, is to put all her customization commands in the
file  /.emacs in her home directory. Emacs reads and executes all
these commands just before starting a session. Such a .emacs file is given
below:
/.emacs in her home directory. Emacs reads and executes all
these commands just before starting a session. Such a .emacs file is given
below:
; Define F1 key to save the buffer
(global-set-key [f1] ’save-buffer)
; Define Control-c s to save the buffer
(global-set-key "\C-cs" ’save-some-buffers)
; Define Meta-s (Alt-s) to interactively search forward
(global-set-key "\M-s" ’isearch-forward)
; Define M-x is to interactively search forward
(defalias ’is ’isearch-forward)
; Define M-x fm to set fortran-mode for the buffer
(defun fm() (interactive) (f90-mode))
; Define M-x sign to sign my name
(defun sign() (interactive) (insert "K. N. Anagnostopoulos"))
Everything after a ; is a comment. Functions/commands are enclosed in
parentheses. The first three ones bind the keys F1, C-c s and M-s to the
commands save-buffer, save-some-buffers and isearch-forward
respectively. The next one defines an alias of a command. This means that,
when we give the command M-x is in the minibuffer, then the command
isearch-forward will be executed. The last two commands are the definitions of
the functions (fm) and (sign), which can be called interactively from the
minibuffer.
For more complicated examples google “emacs .emacs file” and you will see
other users’ .emacs files. You may also customize Emacs from the menu
commands Options Customize Emacs. For learning the Elisp language, you
can read the manual “Emacs Lisp Reference Manual” found at the address
Customize Emacs. For learning the Elisp language, you
can read the manual “Emacs Lisp Reference Manual” found at the address
www.gnu.org/software/emacs/manual/elisp.html
1.4 The Fortran Programming Language
In this section, we give a very basic introduction to the Fortran programming
language. This is not a systematic exposition and you are expected to learn what
is needed in this book by example. So, please, if you have not already done it, get
in front of a computer and do what you read. You can find many good
tutorials and books introducing Fortran in a more complete way in the
bibliography.
1.4.1 The Foundation
The first program that one writes when learning a new programming language is
the “Hello World!” program. This is the program that prints “Hello World!” on
your screen:
program hello
!print a message to the world:
print *, ’Hello World!’ !this is a comment
end program hello
Commands, or statements, in Fortran are strings of characters
separated by blanks (“words”) that we are allowed to write from
the 1st to the 132nd column of a file. Each line starts a new
command .
We can put more than one command on each line by separating them with a
semicolon (;). Everything after an exclamation mark (!) is a comment.
Proliferation of comments is necessary for documenting our code. Good
documentation of our code is an integral part of programming. If the code is
planned to be read by others, or by us at a later time, make sure to explain in
detail what each line is supposed to do. You and your collaborators will save a
lot of time in the process of debugging, improving and extending your
code.
The main entry to the program is defined by the command program
name, where name can be any string of alphanumeric characters and an
underscore. When the program runs, it starts executing commands at
this point. The end of the program, as well as of any other program unit
(functions, subroutines, modules), is defined by the line end program
name.
The first (and only) command given in the above program is the print
command. It prints the string of characters “Hello World!” to the stdout. The
“*,” is part of the syntax and it is not printed, of course. Fortran does not
distinguish capital from small letters, so we could have written PRINT, Print,
prINt, ... A string of characters in Fortran is enclosed in single or double quotes
(’Hello World!’ or "Hello World!" is equivalent).
In order to execute the commands in a program, it is necessary to compile it.
This is a job done by a program called the compiler that translates the
human language programming statements into binary commands that
can be loaded to the computer memory for execution. There are many
Fortran compilers available, and you should learn which compilers are
available for use in your computing environment. Typical names for Fortran
compilers are gfortran, f90, ifort, g95, .... You should find out
which compiler is best suited for your program and spend time reading
its documentation carefully. It is important to learn how to use a new
compiler so that you can finely tune it to optimize the performance of your
program.
We are going to use the open source and freely available compiler
gfortran, which can be installed on most popular operating
systems .
The compilation command is:
> gfortran hello.f90 -o hello
The switch -o defines the name of the executable file, which in our case is hello.
If the compilation is successful, the program runs with the command:
> ./hello
Hello world!
Now, we will try a simple calculation. Given the radius of a circle we
will compute its length and area. The program can be found in the file
area_01.f90:
program circle_area
PI = 3.141593
R = 4.0
print *,’Perimeter= ’,2.0*PI*R
print *,’Area= ’,PI*R**2
end program circle_area
The first two commands define the values of the variables PI and R. These
variables are of type REAL, which are floating point numbers. Fortran
has implicit rules that can be used to define the type of variables. By
default, variables whose name starts with i, j, k, l, m and n are of
INTEGER type. These are exact whole numbers. All other variables are of type
REAL .
We can override these implicit rules by explicitly declaring the type of a variable
or by changing the implicit rules with the use of the implicit statement. The
following two commands have two effects: Computing the length  and the area
and the area  of the circle and printing the results. The expressions
2.0*PI*R and PI*R**2 are evaluated before being printed by the print
command. The multiplication and raising to a power operators are * and **,
respectively. Note the explicit decimal points at the constants 2.0 and 4.0.
If we write 2 or 4 instead, then these are going to be constants of the
INTEGER type and by using them the wrong way we may obtain surprising
results .
We compile and run the program with the commands:
of the circle and printing the results. The expressions
2.0*PI*R and PI*R**2 are evaluated before being printed by the print
command. The multiplication and raising to a power operators are * and **,
respectively. Note the explicit decimal points at the constants 2.0 and 4.0.
If we write 2 or 4 instead, then these are going to be constants of the
INTEGER type and by using them the wrong way we may obtain surprising
results .
We compile and run the program with the commands:
> gfortran area_01.f90 -o area
> ./area
Perimeter= 25.13274
Area= 50.26548
We will now try a process that repeats itself for many times. We will calculate
the length and area of 10 circles of different radii  ,
,  .
We will store the values of the radii in an array R(10) of the REAL type. The code
can be found in the file area_02.f90:
.
We will store the values of the radii in an array R(10) of the REAL type. The code
can be found in the file area_02.f90:
program circle_area
dimension R(10)
PI = 3.141593
R(1) = 2.28
do i=2,10
R(i) = R(i-1) + 1.0
enddo
do i = 1,10
perimeter = 2*PI*R(i)
area = PI*R(i)**2
print *,i,’) R= ’,R(i),’ perimeter= ’,perimeter
print *,i,’) R= ’,R(i),’ area = ’,area
enddo
end program circle_area
The command dimension R(10) defines an array of length 10. This way, the
elements of the array are referred by an index that takes value from 1 to 10. For
example R(4) is the fourth element of the array.
Between the lines
do i = 2, 10
...
enddo
we can write commands that are repeatedly executed while the
INTEGER variable i takes values from 2 to 10 with increasing
step
equal to 1. The command:
R(i) = R(i-1) + 1.0
defines the i-th radius to have a value which is larger by the (i-1)-th by 1. For the loop
to work correctly, we must define the initial value of R(1), otherwise the final result is
undefined .
The second loop uses the defined R-values in order to do the computation and
printing of the results.
Now, we will write an interactive version of the program. Instead of hard
coding the values of the radii, we will interact with the user asking her to
give her own values. The program will read the 10 values of the radii
from the standard input (stdin). The program can be found in the file
area_03.f90:
program circle_area
implicit none
integer,parameter :: N=10
real ,parameter :: PI=3.141593
real ,dimension(N) :: R
real :: area,perimeter
integer :: i
do i=1,N
print*,’Enter radius of circle: ’
read *, R(i)
print*,’i= ’,i,’ R(i)= ’,R(i)
enddo
open(UNIT=13,FILE=’AREA.DAT’)
do i = 1,N
perimeter = 2*PI*R(i)
area = PI*R(i)**2
write(13,*)i,’) R= ’,R(i),’ area= ’,area,&
’ perimeter= ’,perimeter
enddo
close(13)
end program circle_area
The first statement in the above program is implicit none! This statement
deactivates the implicit rules of Fortran, and the programmer is obliged to declare
all variables in a program unit. It is highly recommendable that you always use
this option... You might spend a little more time typing the declarations, but this
effort cannot be compared to the pain looking for bugs due to typos in the names of
variables !
We will follow this practice throughout the book.
The declarations of the variables follow this statement. The variables
N and i are declared to be of the INTEGER type, whereas the variables
PI, area, perimeter and R(N) are declared to be of the REAL type.
The variables PI and N are specified to be parameters. Parameters are
given specific values which cannot be changed during the execution of the
program.
The array elements R(i) are read using the command read:
read *, R(i)
The command read reads from the stdin. The user types the values at the
terminal and then presses [Enter]. We can read more than one variables with one
read command.
In order to print data to a file, we have to connect it to a unit. Each unit is
represented by any number between 0 and 99. Some numbers are reserved for special
units .
The connection of a unit to a file is done with the open
command. When this is done, we can write to the file with the
command
write(n,*), where n is the unit number. When we are done writing to a file we
should use the command close(n). Then the unit number is available to be used
for a different file. The flow of commands is like
open(UNIT=13,FILE=’AREA.DAT’)
...
write(13,*) ....
...
close(13)
The name of the file is determined by the option FILE=’AREA.DAT’ of the open
statement. Uppercase or lowercase characters in the filename make a difference.
The option FILE=’path’ can use any valid path in the filesystem, provided that
we have the necessary permissions.
The line
write(13,*)i,’) R= ’,R(i),’ area= ’,area,&
’ perimeter= ’,perimeter
shows us how to continue a line containing a long statement to the next one. We
place a & at the end of the line and then continue writing the statement to the
next. This can happen up to 39 times.
The next step will be to learn how to define and use functions and subroutines.
The program below shows how to define a subroutine area_of_circle, which
computes the length and area of a circle of given radius. The following program
can be found in the file area_04.f90:
program circle_area
implicit none
integer,parameter :: N=10
real ,parameter :: P=3.141593
real ,dimension(N):: R
real :: area,perimeter
integer :: i
do i=1,N
print*,’Enter radius of circle: ’
read *, R(i)
print*,’i= ’,i,’ R(i)= ’,R(i)
enddo
open(UNIT=13,FILE=’AREA.DAT’)
do i = 1,N
call area_of_circle(R(i),perimeter,area)
write(13,*)i,’) R= ’,R(i),’ area= ’,area,&
’ perimeter= ’,perimeter
enddo
close(13)
end program circle_area
subroutine area_of_circle(R,L,A)
implicit none
real :: R,L,A
real,parameter :: PI = 3.141593 , PI2 = 2.0*PI
L= PI2*R
A= PI*R*R
return
end subroutine area_of_circle
The calculation of the length and the area of the circle is performed by the call
to the subroutine:
call area_of_circle(R(i),perimeter,area)
The command call calls a subroutine and transfers the control of the
program within the subroutine. The above subroutine has the arguments
(R(i),perimeter,area). The argument R(i) is an input variable. It provides the
necessary data to the subroutine in order to perform its computation. The
arguments perimeter and area are intended for output. Upon return of the
subroutine to the main program, they store the result of the computation. The
user of a subroutine must learn how to use its arguments in order to be able to
call it in her program. These must be documented carefully by the programmer of
the subroutine.
The actual program executed by the subroutine is between the lines:
subroutine area_of_circle(R,L,A)
...
end subroutine area_of_circle
The arguments (R,L,A) must be declared in the subroutine and need not have the
same names as the ones that we use when we call it. A change of their values within
the subroutine will change the values of the corresponding variables in the calling
program .
Therefore, the statements L=PI2*R and A=PI*R*R change the values of the
variables perimeter and area to the desired values. The command return
returns the control to the calling program. The parameters PI and PI2 are
“private” to the subroutine. Their names and values are invisible outside the
subroutine. Similarly, the variables i, N, ..., defined in the main program, are
invisible within the subroutine.
We summarize all of the above in a program trionymo.f90, which computes
the roots of a second degree polynomial:
! =============================================================
! Program to compute roots of a 2nd order polynomial
! Tasks: Input from user,logical statements,
! use of functions,stop
! Accuracy in floating point arithmetic
! e.g. IF(x.eq.0.0)
!
! Tests: a,b,c= 1 2 3 D= -8
! a,b,c= 1 -8 16 D= 0 x1= 4
! a,b,c= 1 -1 -2 D= 9. x1= 2. x2= -1.
! a,b,c= 2.3 -2.99 -16.422 x1= 3.4 x2= -2.1
! But: 6.8(x-4.3)**2 = 6.8 x**2 -58.48*x+125.732
! a,b,c= 6.8 -58.48 125.73199
! D= 0.000204147349 x1= 4.30105066 x2= 4.29894924
! a,b,c= 6.8 -58.48 125.732, D= -0.000210891725 < 0!!
! =============================================================
program trionymo
implicit none
real :: a,b,c,D
real :: x1,x2
real :: Discriminant
print*,’Enter a,b,c:’
read *,a,b,c
! Test if we have a well defined polynomial of 2nd degree:
if( a .eq. 0.0) stop ’trionymo: a=0’
! Compute the discriminant (= diakrinousa)
D = Discriminant(a,b,c)
print *, ’Discriminant: D= ’,D
! Compute the roots in each case: D>0, D=0, D<0 (no roots)
if(D .gt. 0.0 )then
call roots(a,b,c,x1,x2)
print *,’Roots: x1= ’,x1,’ x2= ’,x2
else if (D .eq. 0.0) then
call roots(a,b,c,x1,x2)
print *,’Double Root: x1= ’,x1
else
print *,’No real roots’
endif
end program trionymo
! =============================================================
! This is the function that computes the discriminant
! A function returns a value. This value is assigned with the
! statement:
! Discriminant = <value>
! i.e. we simply assign anywhere in the program a variable with
! the name of the function.
! =============================================================
real function Discriminant(a,b,c)
implicit none
real :: a,b,c
Discriminant = b**2 - 4.0 * a * c
end function Discriminant
! =============================================================
! The subroutine that computes the roots.
! =============================================================
subroutine roots(a,b,c,x1,x2)
implicit none
real :: a,b,c
real :: x1,x2
real :: D, Discriminant
if(a .eq. 0.0) stop ’roots: a=0’
D = Discriminant(a,b,c)
if(D.ge.0.0)then
D = sqrt(D)
else
print *,’roots: Sorry, cannot compute roots, D<0=’,D
stop
endif
x1 = (-b + D)/(2.0*a)
x2 = (-b - D)/(2.0*a)
end subroutine roots
The program reads the coefficients of the polynomial  . After a
check whether
. After a
check whether  , it computes the discriminant
, it computes the discriminant  by calling the
function Discriminant(a,b,c). The only difference between a function and a
subroutine is that the first one returns a value of a given type. We don’t need to
use the command call in order to run the commands of a function, this
is done by computing its value in an expression. The type of the value
returned must be declared both in the program that uses the function
(real :: Discriminant) and at the entry point of its program unit (real
function Discriminant(a,b,c)). The value returned to the calling
program is the one assigned to the variable that has the same name as the
function:
by calling the
function Discriminant(a,b,c). The only difference between a function and a
subroutine is that the first one returns a value of a given type. We don’t need to
use the command call in order to run the commands of a function, this
is done by computing its value in an expression. The type of the value
returned must be declared both in the program that uses the function
(real :: Discriminant) and at the entry point of its program unit (real
function Discriminant(a,b,c)). The value returned to the calling
program is the one assigned to the variable that has the same name as the
function:
real function Discriminant(a,b,c)
...
Discriminant = b**2 - 4.0 * a * c
...
end function Discriminant
Notice the use of the comparison operators .gt. (strictly greater than) and .eq.
(equal to) :
if(D .gt. 0.0 )then
...
else if (D .eq. 0.0) then
...
else
...
endif
1.4.2 Details
You may skip this paragraph during a first reading of the book. It is intended
mainly to be a reference when reading the later chapters.
There are more types of variables built in Fortran. In the program listed
below, we show how to use CHARACTER variables, floating point numbers of double
precision REAL(8) and complex numbers of single and double precision, COMPLEX
and COMPLEX(8) respectively:
program f90_vars
implicit none
character(100) :: string
real(4) :: x !single precision, same as real :: x
real(8) :: x8 !equivalent to: double precision x8
!real(16) :: x16 !may not be supported by all compilers
!Complex Numbers:
complex(4) :: z !single precision, same as complex :: z
complex(8) :: z8 !double precision
!A string: a character array:
string = ’Hello World!’ !string smaller size, leaves blanks
!TRIM: trim blanks
print *,’A string ::’, string, ’::’,TRIM(string),’::’
print *,’join them::’, string // string ,’::’
print *,’join them::’, TRIM(string) // TRIM(string),’::’
!Reals with increasing accuracy: Determine PI=3.14159...
x = 4.0 *atan(1.0 )
!Use D for double precision exponent
x8 = 4.0D0*atan(1.0D0)
!Use Q for quadriple precision exponent
!x16 = 4.0Q0*atan(1.0Q0)
print *,’x4= ’,x,’ x8= ’,x8 !,’ x16= ’,x16
print *,’x4: ’,range(x ),precision(x ),EPSILON(x ),&
TINY(x ),HUGE(x )
print *,’x8: ’,range(x8),precision(x8),EPSILON(x8),&
TINY(x8),HUGE(x8)
!Complex numbers: single precision
z = (2.0,1.0)*cexp((3.0,-1.0))
print *,’z= ’,z,’ Re(z)= ’,REAL(z),’ Im(z)= ’,IMAG(z),&
’ |z|= ’,ABS(z),’ z*= ’,CONJG(z)
!Complex numbers: double precision
z8 = (2.0D0,1.0D0)*cdexp((3.0D0,-1.0D0))
print *,’z= ’,z8,’ Re(z)= ’,DBLE(z8),’ Im(z)= ’,DIMAG(z8),&
’ |z|= ’,CDABS(z8),’ z*= ’,DCONJG(z8)
print *,’z4: ’,range(z ),precision(z )
print *,’z8: ’,range(z8),precision(z8)
end program f90_vars
Some interesting points of the program above are:
- The number K in the declaration REAL(K):: x refers to the number of
bytes allocated to the variable x. For K=4 we have single precision (same
as REAL), for K=8 double precision and for K=16 quadruple precision.
The latter is not always available. In the declarations COMPLEX(K), K
refers to the number of bytes allocated to the real and imaginary parts
of the complex number.
- We always use the exponent notation D in double precision constants,
even if the exponent 0. Otherwise the constants are of single precision
and we loose the desired accuracy.
- When we want to state the precision of the return value of an intrinsic
function explicitly, we usually add a d at the beginning of its name
(e.g. exp
 dexp, ABS
dexp, ABS DABS. When we want to use the complex
version of a function, we usually add a c at the beginning of its name
(e.g. exp
DABS. When we want to use the complex
version of a function, we usually add a c at the beginning of its name
(e.g. exp cexp, ABS
cexp, ABS CABS). Modify the program in order to
achieve higher accuracy in the calculation of
CABS). Modify the program in order to
achieve higher accuracy in the calculation of  and
and  ,
by using double precision variables.
,
by using double precision variables.
- The maximum number of characters in the CHARACTER variable string
is 100, and this is declared by the statement CHARACTER(100).
- When we print a CHARACTER variable, all its characters are printed,
including trailing blanks. This is very annoying and we can use the
function TRIM in order to remove them.
- The operator // joins two CHARACTER variables or constants. Notice the
effect of the function TRIM in the above program.
Another important point to discuss is how to be able to access the same variables
from different program units. So far, we simply mentioned that variables have a scope
within each function and subroutine. If we wish to have access to the same location of
memory
from different program units, then we use the COMMON statement which defines a
common block. See the following example:
! ---------------------------------------
program f90_common
implicit none
real :: k1=1.0,k2=1.0,k3=1.0
common /CONSTANTS/k1,k2
print *,’main: k1= ’,k1,’ k2= ’,k2,’ k3= ’,k3
call s1 !prints k1 and k2 but not k3
call s2 !changes the value of k2 but not k3
print *,’main: k1= ’,k1,’ k2= ’,k2,’ k3= ’,k3
end program f90_common
! ---------------------------------------
subroutine s1()
implicit none
real k1,k2,k3
common /CONSTANTS/k1,k2
print *,’s1: k1= ’,k1,’ k2= ’,k2,’ k3= ’,k3
end subroutine s1
! ---------------------------------------
subroutine s2()
implicit none
real k1,k2,k3
common /CONSTANTS/k1,k2
k2 = 2.0
k3 = 2.0
end subroutine s2
The common block has the name CONSTANTS and we can refer to it from any
program unit. Each program unit that uses this common block must use the same
declaration, although the names of variables are allowed to be different. The
common block CONSTANTS points to the same location in the computer memory,
where we expect to find the values of two real variables. These variables (k1 and
k2) are used and have their values changed in the subroutines s1 and s2. The
variable k3, is a different variable in each program unit. The program
prints
main: k1= 1.000000 k2= 1.000000 k3= 1.000000
s1: k1= 1.000000 k2= 1.000000 k3= -2.8117745E-05
main: k1= 1.000000 k2= 2.000000 k3= 1.000000
One of the weaknesses of Fortran is that it does not have a convenient control for
Input/Output (I/O). For complicated I/O and text manipulation we will use
other programs that can do a better job, like awk, perl, shell scripting, or
programs written in C/C++. It is important to know some details about I/O
commands in Fortran, mainly the specifications that control the accuracy of
printed floating point numbers. So far, I/O commands, like print, write, read,
used a * in order to control the printing of numbers. But we can replace the *
with explicit format directives as follows:
program f90_format1
implicit none
integer :: i
real :: x
real, dimension(10) :: a
real(8) :: x8
i = 123456
x = 2.0 *atan2(1.0,0.0)
print ’(A5,I6,F12.7)’,’x,i= ’,i,x
x8 = 2.0D0*atan2(1.0D0,0.0D0)
write(6,’(F18.16,E24.17,G24.17,G24.17)’) x8,x8,&
1.0D15*x8,1.0D18*x8
write(6,’(3F20.16)’) x8,x8/2.0,cos(x8)
write(6,’(200F12.6)’)(a(i), i=1,10)
end program f90_format1
Note the parentheses within the single quotes: (A5,I6,F12.7) is a format
directive for the print statement. The A is for printing a CHARACTER, the I for
printing an INTEGER and the F for printing a floating point number. The numbers
after the letter declare the number of spaces used for printing each one.
Beware! If the printing space is not enough, Fortran will not print and
you will find a series of * in place of the value of your result! Bummer...
In order to estimate the number of spaces needed for a floating point
number, you have to include the space taken by the decimal point, the sign,
the exponent character, the sign of the exponent and the digits needed
for the exponent. Plus a space to separate the numbers in between...
So, be generous and give plenty of printing space. In the example shown
above, A5 denotes a character of 5 spaces, I6 and integer of 6 spaces and
F12 a floating point number of 12 spaces. The decimal point in F12.7
means that we want a floating point with the accuracy of 7 significant
digits.
The format directive (F18.16,E24.17,G24.17,G24.17) shows how to print
double precision variables. These provide an accuracy of 16-17 significant
digits and there is no need for keeping more digits. The command E prints
a number in scientific form with an exponent. The command G prints
the exponent when it is needed. The numbers before the letters denote
multiplicity. Therefore 3F20.16 instructs the printing of 3 floating point
numbers by reserving 20 spaces and using 16 significant digits for each one of
them.
The command write(6,’(200F12.6)’)(a(i), i=1,10) shows how to print a
large array using an implicit loop. We used many more spaces than actually
needed (200F12.16) which is OK. If the array gets larger by increasing the
range of i, then we will have enough room for printing in the same line.
The program prints (we have folded the long line in order to make it
visible):
x,i= 123456 3.1415927
3.1415926535897931 0.31415926535897931E+01 3141592653589793.0
0.31415926535897933E+19
3.1415926535897931 1.5707963267948966 -1.0000000000000000
0.000000 0.000000 0.000000 ....
We can organize the format commands by using the FORMAT statement.
Then, we use labeled statements in order to refer to them. Labels are
numbers put in the beginning of a line which should be unique to a program
unit and are within the range 1-99999. We can transfer the control of the
program to such a line with a goto command or by using the label in
the I/O statements print, write and read as in the example shown
below:
program f90_format2
implicit none
integer i
real x, a(10)
real*8 x8
i = 123456
x = 2.0 *atan2(1.0,0.0)
print 100,’x,i= ’,i,x
x8 = 2.0D0*atan2(1.0D0,0.0D0)
write(6,123) x8,x8,&
1.0D15*x8,1.0D18*x8
write(6,4444) x8,x8/2.0,cos(x8)
write(6,9999)(a(i), i=1,10)
100 FORMAT(A5,I6,F12.7)
123 FORMAT(F18.16,E24.17,G24.17,G24.17)
4444 FORMAT(3F20.16)
9999 FORMAT(200F12.6)
end program f90_format2
The reader should also study the Fortran intrinsic functions shown in table
1.2, page 181.
1.4.3 Arrays
You may skip this section during the first reading of this book. It will be useful to
come back here later.
Arrays are related data of the same type which can be accessed by using one
or more indices. For example, after a declaration real, dimension(10) :: A,
the expressions
A(1), A(2), ... , A(10)
refer to its 10 real values. The indices can be integer expressions, for
example
A(i), B(2*i+3), C(INT(x+y(j)))
where in the last case we used the integer value of the intrinsic function INT(x),
which returns the integer part of x. Note that, arrays and functions enclose indices
and arguments between parentheses (...) which are of the same style, and the
compiler must look at their declarations in order to tell the difference. Examples
of array declarations are
real, dimension(10) :: a,b
real, dimension(20) :: c,d
which declare the arrays a, b, c, d, which are of the real kind, with elements
a(1) ... a(10), b(1) ... b(10), c(1) ... c(20) and d(1) ... d(20). An
equivalent declaration is
real :: a(10), b(10), c(20), d(20)
or
integer, parameter :: n1 = 10, n2 = 20
real, dimension(n1) :: a, c(n2)
real :: b(n1), d(n2)
In the last form, we show how to use constant parameters for declaring the size of
arrays. For the declarations shown above, the lower bound of all arrays is 1 and
the upper bound for a and b is 10 and for c and d is 20. The upper and
lower bound of arrays can be explicitly determined. The declarations
integer, parameter :: n1 = 10, n2 = 20
real, dimension(0:n1) :: a
real, dimension(-n1:n2) :: c
define the real array a with 11 values a(0) ... a(10) and the array c with 31
values c(-10) c(-9) ... c(-1) c(0) c(1) ... c(20).
The arrays shown above have dimension 1 and they are like vectors.
We can declare arrays of more than one dimension. This means
that we need more than one indices in order to determine an array
element .
Therefore, the declaration
integer, dimension(2,2) :: a
defines an integer array with values a(1,1), a(1,2), a(2,1) and a(2,2).
The following declarations define two three dimensional real arrays a and
b:
integer, parameter :: n1 = 10, n2 = 20, n3 = 2*n1+n2
real, dimension(n1,n2,n3) :: a
real, dimension(-n1:n1,0:n2,13:n3) :: b
Some important definitions used in the bibliography are:
- array: Variables of the same type to which we refer with one or more
indices. Variables with only one value are called scalar.
- An array’s dimension has an upper bound and a lower bound
which define the allowed range of index values. If the lower bound is
omitted in a declaration, then it takes the value 1.
- The rank of an array is the number of its dimensions, i.e. the number
of indices needed to determine its values.
- The extent of a dimension it the number of its elements. It is equal to
(upper bound)-(lower bound)+1.
- The size of an array is the total number of its elements. For a one
dimensional array, its size is equal to its extent, whereas for a multi
dimensional one, it is equal to the product of the extents of all of its
dimensions.
- The shape of an array is its rank and extents of all its dimensions.
The values of arrays can be set the same way as scalars:
integer :: i
real :: a(4), b(2,2)
b(1,1) = 2.0 ; b(1,2) = 4.0
b(2,1) = 3.4 ; b(2,2) = 7.8
do i=1,4
a(i) = 1.0
enddo
Alternatively we can use the name of the array as one object:
a = (/ 1.0, 2.0, 3.0, 4.0 /)
b = 0.0
The first line defines the values of an array by using an array constructor. The
second line defines all elements of the array b to be equal to 0. This is an
example of a very convenient feature of the Fortran language. If all the
arrays in an expression are conformable, then we can use the intrinsic
Fortran operations to act on whole arrays. Two arrays are conformable if
they have the same shape or if one of them is a scalar. Therefore the
program
integer :: i,j
real :: x,y,a(10),b(10),c(4,4),d(4,4)
do i=1,10
a(i) = b(i)
enddo
do j=1,4
do i=1,4
c(i,j) = x*d(i,j)+y
enddo
enddo
is equivalent to
integer :: i,j
real :: x,y,a(10),b(10),c(4,4),d(4,4)
a = b
c = x*d+y
Many Fortran intrinsic functions are elemental. This means that their arguments
can be arrays, in which case the function acts on each array element separately.
For example, the commands
integer :: i,j
real :: x,y,a(10),b(10),c(4,4),d(4,4)
c = sin(d) + x*exp(-2.0*d)
call random_number(a)
set c(i,j) = sin(d(i,j))+x*exp(-2.0*d(i,j)) for all i and j, and the
elements of a(i) equal to a random number uniformly distributed in the interval
 . We should stress that in order for two arrays to be conformable, it is not
necessary that they have the same lower and upper bounds. For example, the
command b=c*d in the following program has the same effect as the do
loop:
. We should stress that in order for two arrays to be conformable, it is not
necessary that they have the same lower and upper bounds. For example, the
command b=c*d in the following program has the same effect as the do
loop:
integer :: i
real :: b(0:19), c(10:29), d(-9:10)
b = c*d
do i=1,20
b(i-1) = c(i+9) * d(i-10)
enddo
In the following, we mention some useful functions that act on arrays. Assume
that
real :: a(-10:10), b(-10:10), c(10,10), d(10,10), e(10,10)
then
- LBOUND(a) and UBOUND(a) return the lower bound and the upper
bound of the array a. In the above example LBOUND(a) = -10 and
UBOUND(a) = 10.
- c = TRANSPOSE(d) sets c(i,j)=d(j,i).
- e = MATMUL(c,d) sets the array e equal to the matrix product c, d.
I.e. e(i,j)=
 c(i,k)*d(k,j). Be careful, the command e=c*d
sets e(i,j)=c(i,j)*d(i,j).
c(i,k)*d(k,j). Be careful, the command e=c*d
sets e(i,j)=c(i,j)*d(i,j).
- SUM(a) computes the sum of all the elements of a.
I.e. SUM(a) =  a(i)
a(i)
- PRODUCT(a) computes the product of all the elements of a.
I.e. PRODUCT(a) =  a(i)
a(i)
- DOT_PRODUCT(a,b) computes the inner product of a, b.
I.e. DOT_PRODUCT(a,b) =  a(i)*b(i)
a(i)*b(i)
- MAXVAL(a) and MINVAL(a) return the maximum and minimum values
in the array a respectively.
You can find more functions and documentation in the bibliography [11, 10]. In the
following, we provide some information related to the Input/Output (I/O) of
arrays. Input (“reading”) and output (“writing”) of array values can be
done by reading and writing their elements in any order we want. In the
example below, we read the array a and write the array b in two different
ways:
integer :: i,j
real :: a(4), b(2,2)
do i=1,4
read *,a(i)
enddo
read *, (a(i), i=1,4)
do j=1,2
do i=1,2
print *,b(i,j)
enddo
enddo
print *,( (b(i,j), i=1,2), j=1,2)
Inside the do loops, input and output is done one element per line from/to
standard input/output. The commands (a(i), i=1,4) and ( (b(i,j) i=1,2),
j=1,2) are implied do loops and read/write from/to the same line. During input,
if the number of values for a are exhausted, then the program tries to read
values from the following line(s). Similarly, if the output of b exhausts the
maximum number of characters per line, then the output continues in the next
line .
Try it...
We can also preform I/O of arrays without explicit reference to their elements.
In this case, the arrays are read/written in a specified order. For example, the
program
real :: a(4), b(2,2)
read *, a
read *, b
print *, a,b
reads the values a(1) a(2) a(3) a(4) from the stdin. Then, it continues
reading b(1,1), b(2,1), b(1,2), b(2,2) from the next line (record). Notice
that the array b is read in a column major way. Printing a and b, will print a(1)
a(2) a(3) a(4) and b(1,1), b(2,1), b(1,2), b(2,2) in two different records
(also in column major mode).
Finally, we summarize some of the Fortran capabilities in array manipulation.
More details can be found in the bibliography. Read the comments in the program
for a partial explanation of each command:
program arrays
implicit none
integer :: i,j,n,m
real :: a(3), b(3,3), c(3,3)=-99.0, d(3,3)=-99.0, s
integer :: semester(1000),grade(1000)
logical :: pass(1000)
!construct the matrix: use the RESHAPE function
!|1.1 -1.2 -1.3|
!|2.1 2.2 -2.3|
!|3.1 3.2 3.3|
b = RESHAPE((/ 1.1, 2.1, 3.1, & !(notice rows<->columns)
-1.2, 2.2, 3.2, &
-1.3, -2.3, 3.3 /),(/3,3/))
!same matrix, now exchange rows and columns: ORDER=(/2,1/)
b = RESHAPE((/ 1.2, -1.2, -1.3, &
2.1, 2.2, -2.3, &
3.1, 3.2, 3.3 /),(/3,3/),ORDER=(/2,1/))
a = b(:,2) !a assigned the second column of b: a(i)=b(i,2)
a = b(1,:) !a assigned the first row of b: a(i)=b(1,i)
a = 2.0*b(:,3)+sin(b(2,:))!a(i)= 2*b(i,3)+sin(b(2,i))
a = 1.0+2.0*exp(-a)+b(:,3)!a(i)= 1+2*exp(-a(i))+b(i,3)
s = SUM(b) !returns sum of all elements of b
s = SUM(b,MASK=(b.gt.0))!returns sum of positive elements of b
a = SUM(b,DIM=1) !each a(i) is the sum of the columns of b
a = SUM(b,DIM=2) !each a(i) is the sum of the rows of b
!repeat all the above using PRODUCT!
!all instructions may be executed in parallel at any order!
FORALL(i=1:3) c(i,i) = a(i) !set the diagonal of c
!compute upper bounds of indices in b:
n=UBOUND(b,DIM=1);m=UBOUND(b,DIM=2)
!log needs positive argument, add a restriction ("mask")
FORALL(i=1:n,j=1:m, b(i,j).gt.0.0 ) c(i,j) = log(b(i,j))
!upper triangular part of matrix:
!careful, j=i+1:m NOT permitted
FORALL(i=1:n,j=1:m, i .lt. j ) c(i,j) = b(i,j)
!each statement executed BEFORE the next one!
FORALL(i=2:n-1,j=2:n-1)
!all right hand side evaluated BEFORE the assignment
!i.e., the OLD values of b averaged and then assigned to b
b(i,j)=(b(i+1,j)+b(i-1,j)+b(i,j+1)+b(i,j-1))/4.0
c(i,j)=1.0/b(i+1,j+1) !the NEW values of b are assigned
END FORALL
! assignment but only for elements b(i,j) which are not 0
WHERE (b .ne. 0.0) c = 1.0/b
!MATMUL(b,c) is evaluated, then d is assigned the result only
!at positions where b>0.
WHERE (b .gt. 0.0) d = MATMUL(b,c)
WHERE (grade .ge. 5 )
semester = semester + 1 !student’s semester increases by 1
pass = .true.
ELSEWHERE
pass = .false.
END WHERE
end program arrays
The code shown above can be found in the file f90_arrays.f90 of the
accompanying software.
1.5 Gnuplot
Plotting data is an indispensable tool for their qualitative, but also quantitative,
analysis. Gnuplot is a high quality, open source, plotting program that
can be used for generating publication quality plots, as well as for heavy
duty analysis of a large amount of scientific data. Its great advantage is
the possibility to use it from the command line, as well as from shell
scripts and other programs. Gnuplot is programmable and it is possible to
call external programs in order manipulate data and create complicated
plots. There are many mathematical functions built in gnuplot and a fit
command for non linear fitting of data. There exist interactive terminals
where the user can transform a plot by using the mouse and keyboard
commands.
This section is brief and only the features, necessary for the
following chapters, are discussed. For more information visit the official
page of gnuplot http://gnuplot.info. Try the rich demo gallery at
http://gnuplot.info/screenshots/, where you can find the type of
graph that you want to create and obtain an easy to use recipe for it.
The book [14] is an excellent place to look for many of gnuplot’s
secrets .
You can start a gnuplot session with the gnuplot command:
> gnuplot
G N U P L O T
Version X.XX
....
The gnuplot FAQ is available from www.gnuplot.info/faq/
....
Terminal type set to ’wxt’
gnuplot>
There is a welcome message and then a prompt gnuplot> is issued waiting for
your command. Type a command an press [Enter]. Type quit in order to quit
the program. In the following, when we show a prompt gnuplot>, it is
assumed that the command after the prompt is executed from within
gnuplot.
Plotting a function is extremely easy. Use the command plot and x as the independent variable
of the function .
The command
gnuplot> plot x
plots the function  which is a straight line with slope 1. In order to
plot many functions simultaneously, you can write all of them in one
line:
which is a straight line with slope 1. In order to
plot many functions simultaneously, you can write all of them in one
line:
gnuplot> plot [-5:5][-2:4] x, x**2, sin(x),besj0(x)
The above command plots the functions  ,
,  ,
,  and
and  .
Within the square brackets [:], we set the limits of the
.
Within the square brackets [:], we set the limits of the  and
and  axes,
respectively. The bracket [-5:5] sets
axes,
respectively. The bracket [-5:5] sets  and the bracket
[-2:4] sets
and the bracket
[-2:4] sets  . You may leave the job of setting such
limits to gnuplot, by omitting some, or all of them, from the respective
positions in the brackets. For example, typing [1:][:5] changes the lower
and upper limits of
. You may leave the job of setting such
limits to gnuplot, by omitting some, or all of them, from the respective
positions in the brackets. For example, typing [1:][:5] changes the lower
and upper limits of  and
and  and leaves the upper and lower limits
unchanged .
and leaves the upper and lower limits
unchanged .
In order to plot data points  , we can read their values from files.
Assume that a file data has the following numbers recorded in it:
, we can read their values from files.
Assume that a file data has the following numbers recorded in it:
# x y1 y2
0.5 1.0 0.779
1.0 2.0 0.607
1.5 3.0 0.472
2.0 4.0 0.368
2.5 5.0 0.287
3.0 6.0 0.223
The first line is taken by gnuplot as a comment line, since it begins with a #. In
fact, gnuplot ignores everything after a #. In order to plot the second column as a
function of the first, type the command:
gnuplot> plot "data" using 1:2 with points
The name of the file is within double quotes. After the keyword using, we
instruct gnuplot which columns to use as the  and
and  coordinates, respectively.
The keywords with points instructs gnuplot to add each pair
coordinates, respectively.
The keywords with points instructs gnuplot to add each pair  to the plot
with points.
to the plot
with points.
The command
gnuplot> plot "data" using 1:3 with lines
plots the third column as a function of the first, and the keywords with
lines instruct gnuplot to connect each pair  with a straight line
segment.
with a straight line
segment.
We can combine several plots together in one plot:
gnuplot> plot "data" using 1:3 with points, exp(-0.5*x)
gnuplot> replot "data" using 1:2
gnuplot> replot 2*x
The first line plots the 1st and 3rd columns in the file data together with
the function  . The second line adds the plot of the 1st and 2nd
columns in the file data and the third line adds the plot of the function
. The second line adds the plot of the 1st and 2nd
columns in the file data and the third line adds the plot of the function
 .
.
There are many powerful ways to use the keyword using. Instead of column
numbers, we can put mathematical expressions enclosed inside brackets, like
using (...):(...). Gnuplot evaluates each expression within the brackets and
plots the result. In these expressions, the values of each column in the
file data are represented as in the awk language. $i are variables that
expand to the number read from columns i=1,2,3,.... Here are some
examples:
gnuplot> plot "data" using 1:($2*sin($1)*$3) with points
gnuplot> replot 2*x*sin(x)*exp(-x/2)
The first line plots the 1st column of the file data together with the value
 , where
, where  ,
,  and
and  are the numbers in the 2nd, 1st and
3rd columns respectively. The second line adds the plot of the function
are the numbers in the 2nd, 1st and
3rd columns respectively. The second line adds the plot of the function
 .
.
gnuplot> plot "data" using (log($1)):(log($2**2))
gnuplot> replot 2*x+log(4)
The first line plots the logarithm of the 1st column together with the logarithm
of the square of the 2nd column.
We can plot the data written to the standard output of any command. Assume
that there is a program called area that prints the perimeter and area of a circle
to the stdout in the form shown below:
> ./area
R= 3.280000 area= 33.79851
R= 6.280000 area= 123.8994
R= 5.280000 area= 87.58257
R= 4.280000 area= 57.54895
The interesting data is at the second and fourth columns. These can be plotted
directly with the gnuplot command:
gnuplot> plot "< ./area" using 2:4
All we have to do is to type the full command after the < within the double
quotes. We can create complicated filters using pipes as in the following
example:
gnuplot> plot \
"< ./area|sort -g -k 2|awk ’{print log($2),log($4)}’" \
using 1:2
The filter produces data to the stdout, by combining the action of the
commands area, sort and awk. The data printed by the last program is in two
columns and we plot the results using 1:2.
In order to save plots in files, we have to change the terminal that gnuplot
outputs the plots. Gnuplot can produce plots in several languages (e.g. PDF,
postscript, SVG, LATEX, jpeg, png, gif, etc), which can be interpreted and
rendered by external programs. By redirecting the output to a file, we can save
the plot to the hard disk. For example:
gnuplot> plot "data" using 1:3
gnuplot> set terminal jpeg
gnuplot> set output "data.jpg"
gnuplot> replot
gnuplot> set output
gnuplot> set terminal wxt
The first line makes the plot as usual. The second one sets the output to
be in the JPEG format and the third one sets the name of the file to
which the plot will be saved. The fourth lines repeats all the previous
plotting commands and the fifth one closes the file data.jpg. The last
line chooses the interactive terminal wxt to be the output of the next
plot. High quality images are usually saved in the PDF, encapsulated
postcript or SVG format. Use set terminal pdf,postscript eps or svg,
respectively.
And now a few words for 3-dimensional (3d) plotting. The next example uses
the command splot in order to make a 3d plot of the function  .
After you make the plot, you can use the mouse in order to rotate it and view it
from a different perspective:
.
After you make the plot, you can use the mouse in order to rotate it and view it
from a different perspective:
gnuplot> set pm3d
gnuplot> set hidden3d
gnuplot> set size ratio 1
gnuplot> set isosamples 50
gnuplot> splot [-2:2][-2:2] exp(-x**2-y**2)
If you have data in the form  and you want to create a plot of
and you want to create a plot of
 , write the data in a file, like in the following example:
, write the data in a file, like in the following example:
-1 -1 2.000
-1 0 1.000
-1 1 2.000
0 -1 1.000
0 0 0.000
0 1 1.000
1 -1 2.000
1 0 1.000
1 1 2.000
Note the empty line that follows the change of the value of the first column. If
the name of the file is data3, then you can plot the data with the commands:
gnuplot> set pm3d
gnuplot> set hidden3d
gnuplot> set size ratio 1
gnuplot> splot "data3" with lines
We close this section with a few words on parametric plots. A parametric
plot on the plane (2-dimensions) is a curve  , where
, where  is a
parameter. A parametric plot in space (3-dimensions) is a surface
is a
parameter. A parametric plot in space (3-dimensions) is a surface 

 , where
, where  are parameters. The following commands
plot the circle
are parameters. The following commands
plot the circle  and the sphere
and the sphere 

 :
:
gnuplot> set parametric
gnuplot> plot sin(t),cos(t)
gnuplot> splot cos(u)*cos(v),cos(u)*sin(v),sin(u)
1.6 Shell Scripting
Complicated system administration tasks are not among the strengths of the
Fortran programming language. But in a typical GNU/Linux environment, there
exist many powerful tools that can be used very effectively for this purpose. This
way, one can use Fortran for the high performance and scientific computing part
of the project and leave the administration and trivial data analysis tasks to
other, external, programs.
One can avoid repeating the same sequence of commands by coding them in a
file. An example can be found in the file script01.csh:
#!/bin/tcsh -f
gfortran area_01.f90 -o area
./area
gfortran area_02.f90 -o area
./area
gfortran area_03.f90 -o area
./area
gfortran area_04.f90 -o area
./area
This is a very simple shell script. The first line instructs the operating
system that the lines that follow are to be interpreted by the program
/bin/tcsh .
This can be any program in the system, which in our case is the tcsh shell.
The following lines are valid commands for the shell, one in each line.
They compile the Fortran programs found in the files that we created in
section 1.4 with gfortran, and then they run the executable ./area. In
order to execute the commands in the file, we have to make sure that the
file has the appropriate execute permissions. If not, we have to give the
command:
> chmod u+x script01.csh
Then we simply type the path to the file script01.csh
> ./script01.csh
and the above commands are run the one after the other. Some of the versions of
the programs that we wrote are asking for input from the stdin, which, normally,
you have to type on the terminal. Instead of interacting directly with
the program, we can write the input data to a file Input, and run the
command
./area < Input
A more convenient solution is to use the, so called, “Here Document”.
A “Here Document” is a section of the script that is treated as if it
were a separate file. As such, it can be used as input to programs by
sending its “contents” to the stdin of the command that runs the
program .
The “Here Document” does not appear in the filesystem and we don’t need to
administer it as a regular file. An example of using a “Here Document” can be
found in the file script02.csh:
#!/bin/tcsh -f
gfortran area_04.f90 -o area
./area <<EOF
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
EOF
The stdin of the command ./area is redirected to the contents between the
lines
./area <<EOF
...
EOF
The string EOF marks the beginning and the end of the “Here Document”, and
can be any string you like. The last EOF has to be placed exactly in the beginning
of the line.
The power of shell scripting lies in its programming capabilities: Variables,
arrays, loops and conditionals can be used in order to create a complicated
program. Shell variables can be used as discussed in section 1.1.2: The value of a
variable name is $name and it can be set with the command set name = value.
An array is defined, for example, by the command
set R = (1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0)
and its data can be accessed using the syntax $R[1] ... $R[10].
Lets take a look at the following script:
#!/bin/tcsh -f
set files = (area_01.f90 area_02.f90 area_03.f90 area_04.f90)
set R = (1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0)
echo "Hello $USER Today is " ‘date‘
foreach file ($files)
echo "# ----------- Working on file $file "
gfortran $file -o area
./area <<EOF
$R[1]
$R[2]
$R[3]
$R[4]
$R[5]
$R[6]
$R[7]
$R[8]
$R[9]
$R[10]
EOF
echo "# ----------- Done "
if( -f AREA.DAT ) cat AREA.DAT
end
The first two lines of the script define the values of the arrays files (4 values)
and R (10 values). The command echo echoes its argument to the stdin. $USER is
the name of the user running the script. ‘date‘ is an example of command
substitution: When a command is enclosed between backquotes and is part of
a string, then the command is executed and its stdout is pasted back
to the string. In the example shown above, ‘date‘ is replaced by the
current date and time in the format produced by the date command.
The foreach loop
foreach file ($files)
...
end
is executed once for each of the 4 values of the array files. Each time the
value of the variable file is set equal to one of the values area_01.f90,
area_02.f90, area_03.f90, area_04.f90. These values can be used by
the commands in the loop. Therefore, the command gfortran $file
-o area compiles a different file each time that it is executed by the
loop.
The last line in the loop
if( -f AREA.DAT ) cat AREA.DAT
is a conditional. It executes the command cat AREA.DAT if the condition -f
AREA.DAT is true. In this case, -f constructs a logical expression which is true
when the file AREA.DAT exists.
We close this section by presenting a more complicated and advanced
script. It only serves as a demonstration of the shell scripting capabilities.
For more information, the reader is referred to the bibliography
[16, 17, 18, 19, 20]. Read carefully the commands, as well as the
comments which follow the # mark. Then, write the commands to a file
script04.csh ,
make it an executable file with the command chmod u+x script04.csh and give
the command
> ./script04.csh This is my first serious tcsh script
The script will run with the words “This is my first serious tcsh script” as its
arguments. Notice how these arguments are manipulated by the script.
Then, the script asks for the values of the radii of ten or more circles
interactively, so that it will compute their perimeter and area. Type them on the
terminal and then observe the script’s output, so that you understand the
function of each command. You will not regret the time investment!
#!/bin/tcsh -f
# Run this script as:
# ./script04.csh Hello this is a tcsh script
#----------------------------------------------------------------------
# ‘command‘ is command substitution: it is replaced by stdout of command
set now = ‘date‘ ; set mypc = ‘uname -a‘
# Print information: variables are expanded within double quotes
echo "I am user $user working on the computer $HOST" #HOST is predefined
echo "Today the date is : $now" #now is defined above
echo "My home directory is : $home" #home is predefined
echo "My current directory is: $cwd" #cwd changes with cd
echo "My computer runs : $mypc" #mypc is defined above
echo "My process id is : $$ " #$$ is predefined
# Manipulate the command line: ($#argv is number of elements in array argv)
echo "The command line has $#argv arguments"
echo "The name of the command I am running is: $0"
echo "Arguments 3rd to last of the command : $argv[3-]" #third to last
echo "The last argument is : $argv[$#argv]" #last element
echo "All arguments : $argv"
# Ask user for input: enter radii of circles
echo -n "Enter radii of circles: " # variable $< stores one line of input
set Rs = ($<) #Rs is now an array with all words entered by user
if($#Rs < 10 )then #make a test, need at least 10 of them
echo "Need more than 10 radii. Exiting...."
exit(1)
endif
echo "You entered $#Rs radii, the first is $Rs[1] and the last $Rs[$#Rs]"
echo "Rs= $Rs"
# Now, compute the perimeter of each circle:
foreach R ($Rs)
# -v rad=$R set the awk variable rad equal to $R. pi=atan2(0,-1)=3.14...
set l = ‘awk -v rad=$R ’BEGIN{print 2*atan2(0,-1)*rad}’‘
echo "Circle with R= $R has perimeter $l"
end
# alias defines a command to do what you want: use awk as a calculator
alias acalc ’awk "BEGIN{print \!* }"’ # \!* substitutes args of acalc
echo "Using acalc to compute 2+3=" ‘acalc 2+3‘
echo "Using acalc to compute cos(2*pi)=" ‘acalc cos(2*atan2(0,-1))‘
# Now do the same loop over radii as above in a different way
# while( expression ) is executed as long as "expression" is true
while($#Rs > 0) #executed as long as $Rs contains radii
set R = $Rs[1] #take first element of $Rs
shift Rs #now $Rs has one less element:old $Rs[1] has vanished
set a = ‘acalc atan2(0,-1)*${R}*${R}‘ # =pi*R*R calculated by acalc
# construct a filename to save the result from the value of R:
set file = area${R}.dat
echo "Circle with R= $R has area $a" > $file #save result in a file
end #end while
# Now look for our files: save their names in an array files:
set files = (‘ls -1 area*.dat‘)
if( $#files == 0) echo "Sorry, no area files found"
echo "--------------------------------------------"
echo "files: $files"
ls -l $files
echo "--------------------------------------------"
echo "And the results for the area are:"
foreach f ($files)
echo -n "file ${f}: "
cat $f
end
# now play a little bit with file names:
echo "--------------------------------------------"
set f = $files[1] # test permissions on first file
# -f, -r, -w, -x, -d test existence of file, rwxd permissions
# the ! negates the expression (true -> false, false -> true)
echo "testing permissions on files:"
if( -f $f ) echo "$file exists"
if( -r $f ) echo "$file is readable by me"
if( -w $f ) echo "$file is writable by be"
if(! -w /bin/ls) echo "/bin/ls is NOT writable by me"
if(! -x $f ) echo "$file is NOT an executable"
if( -x /bin/ls) echo "/bin/ls is executable by me"
if(! -d $f ) echo "$file is NOT a directory"
if( -d /bin ) echo "/bin is a directory"
echo "--------------------------------------------"
# transform the name of a file
set f = $cwd/$f # add the full path in $f
set filename = $f:r # removes extension .dat
set extension = $f:e # gets extension .dat
set fdir = $f:h # gets directory of $f
set base = ‘basename $f‘ # removes directory name
echo "file is: $f"
echo "filename is: $filename"
echo "extension is: $extension"
echo "directory is: $fdir"
echo "basename is: $base"
# now transform the name to one with different extension:
set newfile = ${filename}.jpg
echo "jpeg name is: $newfile"
echo "jpeg base is:" ‘basename $newfile‘
if($newfile:e == jpg)echo ‘basename $newfile‘ " is a picture"
echo "--------------------------------------------"
# Now save all data in a file using a "here document"
# A here document starts with <<EOF and ends with a line
# starting exactly with EOF (EOF can be any string as below)
# In a "here document" we can use variables and command
# substitution:
cat <<AREAS >> areas.dat
# This file contains the areas of circle of given radii
# Computation done by ${user} on ${HOST}. Today is ‘date‘
‘cat $files‘
AREAS
# now see what we got:
if( -f areas.dat) cat areas.dat
# You can use a "here document" as standard input to any command:
# use gnuplot to save a plot: gnuplot does the job and exits...
gnuplot <<GNU
set terminal jpeg
set output "areas.jpg"
plot "areas.dat" using 4:7 title "areas.dat",\
pi*x*x title "pi*R^2"
set output
GNU
# check our results: display the jpeg file using eog
if( -f areas.jpg) eog areas.jpg &
|
|
| awk | search for and process patterns in a file, |
| cat | display, or join, files |
| cd | change working directory |
| chmod | change the access mode of a file |
| cp | copy files |
| date | display current time and date |
| df | display the amount of available disk space |
| diff | display the differences between two files |
| du | display information on disk usage |
| echo | echo a text string to output |
| find | find files |
| grep | search for a pattern in files |
| gzip | compress files in the gzip (.gz) format (gunzip to uncompress) |
| head | display the first few lines of a file |
| kill | send a signal (like KILL) to a process |
| locate | search for files stored on the system (faster than find) |
| less | display a file one screen at a time |
| ln | create a link to a file |
| lpr | print files |
| ls | list information about files |
| man | search information about command in man pages |
| mkdir | create a directory |
| mv | move and/or rename a file |
| ps | report information on the processes run on the system |
| pwd | print the working directory |
| rm | remove (delete) files |
| rmdir | remove (delete) a directory |
| sort | sort and/or merge files |
| tail | display the last few lines of a file |
| tar | store or retrieve files from an archive file |
| top | dynamic real-time view of processes |
| wc | counts lines, words and characters in a file |
| whatis | list man page entries for a command |
| where | show where a command is located in the path (alternatively: whereis) |
| which | locate an executable program using ”path” |
| zip | create compressed archive in the zip format (.zip) |
| unzip | get/list contents of zip archive |
|
|
| |
Table 1.1: Basic Unix commands.
Table 1.2: Some intrinsic functions in Fortran.
|
|
|
| Function |
Description |
|
|
| |
| | |
| ABS |
modulus of a complex number, absolute
value of number |
| ACOS |
arccosine of a number |
| ADJUSTL |
moves non blank characters of a string to the
left |
| ADJUSTR |
moves non blank characters of a string to the
right |
| AIMAG |
imaginary part of a complex number |
| AINT |
truncates fractional part but preserves data
type |
| ANINT |
rounds to nearest whole number but
preserves data type |
| ASIN |
arcsine of a number |
| ATAN |
arctangent of a number |
| ATAN2 |
arctangent of arg1 divided by arg2 resolved
into the correct quadrant |
| CMPLX |
converts to the COMPLEX data type arg1
+ i arg2 |
| CONJG |
complex conjugate of a complex number |
| COS |
cosine of an angle in radians |
| COSH |
hyperbolic cosine |
| DATE_AND_TIME |
returns current date and time |
| DBLE |
converts to the real(8) data type |
| DIM |
if arg1  arg2, then returns arg1 - arg2;
otherwise 0 arg2, then returns arg1 - arg2;
otherwise 0 |
| DPROD |
double precision product of two single
precision numbers |
| EXP |
exponential |
| EPSILON |
Returns a positive number that is negligible
compared to 1.0 |
| |
| HUGE |
Returns the largest number of the same kind
as the argument |
| INT |
converts to the INTEGER data type by
truncation |
| KIND |
Returns the KIND value of argument |
| LEN |
Returns the length of a string |
| LEN_TRIM |
returns the length of a string without trailing
blanks |
| LGE,LGT,LLE,LLT |
string comparison functions |
| LOG |
natural logarithm |
| LOG10 |
common logarithm |
| MAX |
maximum value of arguments |
| MAXEXPONENT |
returns the maximum exponent of the same
kind as the argument |
| MIN |
minimum value of arguments |
| MINEXPONENT |
returns the minimum exponent of the same
kind as the argument |
| MOD |
arg1 modulo arg2 |
| NINT |
converts to the INTEGER data type by
rounding |
| RANDOM_NUMBER |
returns pseudo-random numbers  |
| RANDOM_SEED |
starts random number generator or returns
generator parameters |
| PRECISION |
returns the decimal precision of the same
kind as the argument |
| REAL |
real part of a complex number |
| REAL |
converts to the REAL data type |
| SIGN |
if arg2  0, then returns -arg1; else +arg1 0, then returns -arg1; else +arg1 |
| |
| SIN |
sine of an angle in radians |
| SINH |
hyperbolic sine |
| SQRT |
square root |
| TAN |
tangent of an angle in radians |
| TANH |
hyperbolic tangent |
| TINY |
returns the smallest positive number of the
same kind as the argument |
| TRIM |
returns string with trailing blanks removed |
|
|
Array functions
|
|
|
| ALL |
true if all values are true |
| ALLOCATED |
array allocation status |
| ANY |
true if any values are true |
| COUNT |
number of elements in an array |
| DOT_PRODUCT |
dot product of two rank-one arrays |
| LBOUND |
lower dimension bounds of an array |
| MATMUL |
matrix multiplication |
| MAXLOC |
location of a maximum value in an array |
| MAXVAL |
maximum value in an array |
| MERGE |
merge arrays under mask |
| MINLOC |
location of a minimum value in an array |
| MINVAL |
minimum value in an array |
| |
| PACK |
pack an array into an array of rank one under
a mask |
| PRODUCT |
product of array elements |
| RESHAPE |
reshape an array |
| SHAPE |
shape of an array or scalar |
| SIZE |
size of an array |
| SPREAD |
replicate an array by adding a dimension |
| SUM |
sum of array elements |
| TRANSPOSE |
transpose an array of rank two |
| UBOUND |
upper dimension bounds of an array |
| UNPACK |
unpack an array of rank one into an array
under a mask |
| |
| |
| |
| |
| |
|
|
|
|
Table 1.3: Basic Emacs commands.
|
|
|
|
|
| | |
|
|
|
Leaving Emacs
|
|
|
|
| suspend Emacs (or iconify it under X) | C-z | |
| exit Emacs permanently | C-x C-c | |
|
|
|
Files
|
|
|
|
| read a file into Emacs | C-x C-f | |
| save a file back to disk | C-x C-s | |
| save all files | C-x s | |
| insert contents of another file into this buffer | C-x i | |
| toggle read-only status of buffer | C-x C-q | |
|
|
|
Getting Help
|
|
|
|
The help system is simple. Type C-h (or F1) and follow the directions. If you
are a first-time user, type C-h t for a tutorial.
|
| remove help window | C-x 1 | |
| apropos: show commands matching a string | C-h a | |
| describe the function a key runs | C-h k | |
| describe a function | C-h f | |
| get mode-specific information | C-h m | |
|
|
|
Error Recovery
|
|
|
|
| abort partially typed or executing command | C-g | |
| recover files lost by a system crash | M-x recover-session | |
| undo an unwanted change | C-x u, C-_ or C-/ | |
| |
| restore a buffer to its original contents | M-x revert-buffer | |
| redraw garbaged screen | C-l | |
|
|
|
Incremental Search
|
|
|
|
| search forward | C-s | |
| search backward | C-r | |
| regular expression search | C-M-s | |
| abort current search | C-g | |
Use C-s or C-r again to repeat the search in either direction. If Emacs is still
searching, C-g cancels only the part not matched.
|
|
|
|
Motion
|
|
|
|
| entity to move over | backward | forward |
| character | C-b | C-f |
| word | M-b | M-f |
| line | C-p | C-n |
| go to line beginning (or end) | C-a | C-e |
| go to buffer beginning (or end) | M-< | M-> |
| scroll to next screen | C-v | |
| scroll to previous screen | M-v | |
| scroll left | C-x < | |
| scroll right | C-x > | |
| scroll current line to center of screen | C-u C-l | |
| |
|
|
|
Killing and Deleting
|
|
|
|
| entity to kill | backward | forward |
| character (delete, not kill) | DEL | C-d |
| word | M-DEL | M-d |
| line (to end of) | M-0 C-k | C-k |
| kill region | C-w | |
| copy region to kill ring | M-w | |
| yank back last thing killed | C-y | |
| replace last yank with previous kill | M-y | |
|
|
|
Marking
|
|
|
|
| set mark here | C-@ or C-SPC | |
| exchange point and mark | C-x C-x | |
| mark paragraph | M-h | |
| mark entire buffer | C-x h | |
|
|
|
Query Replace
|
|
|
|
| interactively replace a text string | M-% or M-x query-replace | |
| using regular expressions | M-x query-replace-regexp | |
|
|
|
Buffers
|
|
|
|
| select another buffer | C-x b | |
| list all buffers | C-x C-b | |
| |
| kill a buffer | C-x k | |
|
|
|
|
|
|
|
|
When two commands are shown, the second is a similar command for a frame
instead of a window.
|
| delete all other windows | C-x 1 | C-x 5 1 |
| split window, above and below | C-x 2 | C-x 5 2 |
| delete this window | C-x 0 | C-x 5 0 |
| split window, side by side | C-x 3 | |
| switch cursor to another window | C-x o | C-x 5 o |
| grow window taller | C-x ^ | |
| shrink window narrower | C-x { | |
| grow window wider | C-x } | |
|
|
|
Formatting
|
|
|
|
| indent current line (indent code etc) | TAB | |
| insert newline after point | C-o | |
| fill paragraph | M-q | |
|
|
|
Case Change
|
|
|
|
| uppercase word | M-u | |
| lowercase word | M-l | |
| capitalize word | M-c | |
| uppercase region | C-x C-u | |
| |
| lowercase region | C-x C-l | |
|
|
|
|
|
|
|
|
The following keys are defined in the minibuffer.
|
| complete as much as possible | TAB | |
| complete up to one word | SPC | |
| complete and execute | RET | |
| abort command | C-g | |
Type C-x ESC ESC to edit and repeat the last command that used the
minibuffer. Type F10 to activate menu bar items on text terminals.
|
|
|
|
|
|
|
|
|
| check spelling of current word | M-$ | |
| check spelling of all words in region | M-x ispell-region | |
| check spelling of entire buffer | M-x ispell-buffer | |
| On the fly spell checking | M-x flyspell-mode | |
|
|
|
Info – Getting Help Within Emacs
|
|
|
|
| enter the Info documentation reader | C-h i | |
| scroll forward | SPC | |
| scroll reverse | DEL | |
| next node | n | |
| previous node | p | |
| move up | u | |
| |
| select menu item by name | m | |
| return to last node you saw | l | |
| return to directory node | d | |
| go to top node of Info file | t | |
| go to any node by name | g | |
| quit Info | q | |
| |
| |
| |
| |
| |
|
|
|
|
|
Chapter 2
Kinematics
In this chapter we show how to program simple
kinematic equations of motion of a particle and how to do basic analysis of
numerical results. We use simple methods for plotting and animating trajectories
on the two dimensional plane and three dimensional space. In section 2.3 we study
numerical errors in the calculation of trajectories of freely moving particles
bouncing off hard walls and obstacles. This will be a prelude to the study of the
integration of the dynamical equations of motion that we will introduce in the
following chapters.
2.1 Motion on the Plane
When a particle moves on the plane, its position can be given in Cartesian
coordinates  . These, as a function of time, describe the particle’s
trajectory. The position vector is
. These, as a function of time, describe the particle’s
trajectory. The position vector is  , where
, where  and
and  are the
unit vectors on the
are the
unit vectors on the  and
and  axes respectively. The velocity vector is
axes respectively. The velocity vector is
 where
where
The acceleration  is given by
is given by
In this section we study the kinematics of a particle trajectory, therefore we
assume that the functions  are known. By taking their derivatives, we
can compute the velocity and the acceleration of the particle in motion. We will
write simple programs that compute the values of these functions in a time
interval
are known. By taking their derivatives, we
can compute the velocity and the acceleration of the particle in motion. We will
write simple programs that compute the values of these functions in a time
interval ![[t0,tf]](main_latex102x.png) , where
, where  is the initial and
is the initial and  is the final time. The continuous
functions
is the final time. The continuous
functions  are approximated by a discrete sequence
of their values at the times
are approximated by a discrete sequence
of their values at the times  such that
such that
 .
.
We will start the design of our program by forming a generic template to be
used in all of the problems of interest. Then we can study each problem of particle
motion by programming only the equations of motion without worrying about the
less important tasks, like input/output, user interface etc. Figure 2.2 shows a
flowchart of the basic steps in the algorithm. The first part of the program
declares variables and defines the values of the fixed parameters (like
 ,
,  , etc). The program starts by interacting with
the user (“user interface”) and asks for the values of the variables
, etc). The program starts by interacting with
the user (“user interface”) and asks for the values of the variables  ,
,
 ,
,  ,
,  ,
,  . The program prints these values to the stdout
so that the user can check them for correctness and store them in her
data.
. The program prints these values to the stdout
so that the user can check them for correctness and store them in her
data.
The main calculation is performed in a loop executed while  . The values
of the positions and the velocities
. The values
of the positions and the velocities  are calculated and
printed in a file together with the time
are calculated and
printed in a file together with the time  . At this point we fix the format
of the program output, something that is very important to do it in a
consistent and convenient way for easing data analysis. We choose to
print the values t, x, y, vx, vy in five columns in each line of the output
file.
. At this point we fix the format
of the program output, something that is very important to do it in a
consistent and convenient way for easing data analysis. We choose to
print the values t, x, y, vx, vy in five columns in each line of the output
file.
The specific problem that we are going to solve is the computation of the
trajectory of the circular motion of a particle on a circle with center  and radius
and radius  with constant angular velocity
with constant angular velocity  . The position on the
circle can be defined by the angle
. The position on the
circle can be defined by the angle  , as can be seen in figure 2.3. We
define the initial position of the particle at time
, as can be seen in figure 2.3. We
define the initial position of the particle at time  to be
to be  .
.
The equations giving the position of the particle at time  are
are
Taking the derivative w.r.t.  we obtain the velocity and the acceleration We note that the above equations imply that
we obtain the velocity and the acceleration We note that the above equations imply that  (
( ,
,  ,
,
 tangent to the trajectory) and
tangent to the trajectory) and  (
( and
and  anti-parallel,
anti-parallel,
 ).
).
The data structure is quite simple. The constant angular velocity  is stored
in the REAL variable omega. The center of the circle
is stored
in the REAL variable omega. The center of the circle  , the radius
, the radius  of the
circle and the angle
of the
circle and the angle  are stored in the REAL variables x0, y0, R, theta. The
times at which we calculate the particle’s position and velocity are defined
by the parameters
are stored in the REAL variables x0, y0, R, theta. The
times at which we calculate the particle’s position and velocity are defined
by the parameters  and are stored in the REAL variables t0,
tf, dt. The current position
and are stored in the REAL variables t0,
tf, dt. The current position  is calculated and stored in the
REAL variables x, y and the velocity
is calculated and stored in the
REAL variables x, y and the velocity  in the REAL variables
vx, vy. The declarations of the variables are put in the beginning of the
program:
in the REAL variables
vx, vy. The declarations of the variables are put in the beginning of the
program:
real :: x0,y0,R,x,y,vx,vy,t,t0,tf,dt
real :: theta,omega
real, parameter :: PI=3.1415927
were we defined the value
of  by using the parameter specification.
by using the parameter specification.
The user interface of the program is the interaction of the program with the
user and, in our case, it is the part of the program where the user enters the
parameters omega, x0, y0, R, t0, tf, dt. The program issues a prompt
with the names the variables expected to be read. This is done using
simple print statements. The variables are read from the stdin by simple
read statements and the values entered by the user are printed to the
stdout :
print *,’# Enter omega:’
read *,omega
print *,’# Enter center of circle (x0,y0) and radius R:’
read *,x0,y0,R
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# omega= ’,omega
print *,’# x0= ’,x0,’ y0= ’,y0,’ R= ’,R
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
Next, the program initializes the state of the computation. This includes checking
the validity of the parameters entered by the user, so that the computation will be
possible. For example, the program computes the expression 2.0*PI/omega, where
it is assumed that omega has a non zero value. We will also demand that
 and
and  . An if statement will make those checks and if the
parameters have illegal values, the stop statement will stop the program
execution .
The program opens the file Circle.dat for writing the calculated values of the
position and the velocity of the particle.
. An if statement will make those checks and if the
parameters have illegal values, the stop statement will stop the program
execution .
The program opens the file Circle.dat for writing the calculated values of the
position and the velocity of the particle.
if(R .le. 0.0) stop ’Illegal value of R’
if(omega .le. 0.0) stop ’Illegal value of omega’
print *,’# T= ’,2.0*PI/omega
open(unit=11,file=’Circle.dat’)
If  or
or  the corresponding stop statements are executed which end
the program execution. The optional error messages are included after the stop
statements which are printed to the stdout. The value of the period
the corresponding stop statements are executed which end
the program execution. The optional error messages are included after the stop
statements which are printed to the stdout. The value of the period  is also calculated and printed for reference.
is also calculated and printed for reference.
The open statement uses unit 11 for writing to the file Circle.dat.
The choice of the unit number is free for the programmer to choose.
We recommend using the units 10 to 99 for input/output to
files .
The main calculation is performed within the loop
t = t0
do while(t .le. tf)
.........
t = t + dt
enddo
The first statement sets the initial value of the time. The statements between the
do while(condition) and enddo are executed as long as condition has a .TRUE.
value. The statement t=t+dt increments the time and this is necessary in order
not to enter into an infinite loop. he commands put in place of the dots
......... calculate the position and the velocity and print them to the file
Circle.dat:
theta = omega * (t-t0)
x = x0+R*cos(theta)
y = y0+R*sin(theta)
vx = -omega*R*sin(theta)
vy = omega*R*cos(theta)
write(11,*)t,x,y,vx,vy
Notice the use of the intrinsic functions sin and cos that calculate the sine
and cosine of an angle expressed in radians. We use the intermediate
variable theta in order to store the phase  . The command
write(11,*) writes the variables t,x,y,vx,vy to the unit 11, which has
been associated to the file Circle.dat with the open statement shown
above.
. The command
write(11,*) writes the variables t,x,y,vx,vy to the unit 11, which has
been associated to the file Circle.dat with the open statement shown
above.
The program is stored in the file Circle.f90 and can be found in the
accompanied software. The extension .f90 is used by the compiler in order to
denote source code written in free format Fortran language. Compilation and
running can be done using the commands:
> gfortran Circle.f90 -o cl
> ./cl
The switch -o cl forces the compiler gfortran to write the binary commands executed by the
program to the file
cl. The command ./cl loads the program instructions to the computer memory
for execution. When the programs starts execution, it first asks for the
parameter data and then performs the calculation. A typical session looks
like:
> gfortran Circle.f90 -o cl
> ./cl
# Enter omega:
1.0
# Enter center of circle (x0,y0) and radius R:
1.0 1.0 0.5
# Enter t0,tf,dt:
0.0 20.0 0.01
# omega= 1.
# x0= 1. y0= 1. R= 0.5
# t0= 0. tf= 20. dt= 0.00999999978
# T= 6.28318548
The lines shown above that start with a # character are printed by the program
and lines without # are the values of the parameters entered interactively by the
user. The user types in the parameters and then presses the Enter key in order for
the program to read them. Here we have  ,
,  ,
,  ,
,
 ,
,  and
and  .
.
You can execute the above program many times for different values of the
parameter by writing the parameter values in a file using an editor. For example,
in the file Circle.in type the following data:
1.0 omega
1.0 1.0 0.5 (x0, y0) , R
0.0 20.0 0.01 t0 tf dt
Each line has the parameters read by the program with a read statement (a
record). The rest of the line is ignored by the program and the user can write
anything she likes as a comment on how to use the parameters. The program can
read the above values of the parameters with the command:
> ./cl < Circle.in > Circle.out
The command ./cl runs the commands found in the executable file ./cl. The <
Circle.in redirects the contents of the file Circle.in to the standard input
(stdin) of the command ./cl. This way the program reads in the values of the
parameters from the contents of the file Circle.in. The > Circle.out redirects
the standard output (stdout) of the command ./cl to the file Circle.out. Its
contents can be inspected after the execution of the program with the command
cat:
> cat Circle.out
# Enter omega:
# Enter center of circle (x0,y0) and radius R:
# Enter t0,tf,dt:
# omega= 1.
# x0= 1. y0= 1. R= 0.5
# t0= 0. tf= 20. dt= 0.00999999978
# T= 6.28318548
We list the full program in Circle.f90 below:
!============================================================
!File Circle.f90
!Constant angular velocity circular motion
!Set (x0,y0) center of circle, its radius R and omega.
!At t=t0, the particle is at theta=0
!------------------------------------------------------------
program Circle
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: x0,y0,R,x,y,vx,vy,t,t0,tf,dt
real :: theta,omega
real, parameter :: PI=3.1415927
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter omega:’
read *,omega
print *,’# Enter center of circle (x0,y0) and radius R:’
read *,x0,y0,R
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# omega= ’,omega
print *,’# x0= ’,x0,’ y0= ’,y0,’ R= ’,R
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
if(R .le. 0.0) stop ’Illegal value of R’
if(omega .le. 0.0) stop ’Illegal value of omega’
print *,’# T= ’,2.0*PI/omega
open(unit=11,file=’Circle.dat’)
!------------------------------------------------------------
!Compute:
t = t0
do while(t .le. tf)
theta = omega * (t-t0)
x = x0+R*cos(theta)
y = y0+R*sin(theta)
vx = -omega*R*sin(theta)
vy = omega*R*cos(theta)
write(11,*)t,x,y,vx,vy
t = t + dt
enddo
close(11)
end program Circle
2.1.1 Plotting Data
We use gnuplot for plotting the data produced by our programs. The file
Circle.dat has the time t and the components x, y, vx, vy in five columns.
Therefore we can plot the functions  and
and  by using the gnuplot
commands:
by using the gnuplot
commands:
gnuplot> plot "Circle.dat" using 1:2 with lines title "x(t)"
gnuplot> replot "Circle.dat" using 1:3 with lines title "y(t)"
The second line puts the second plot together with the first one. The results
can be seen in figure 2.4.
Let’s see now how we can make the plot of the function  . We can do that using
the raw data from the file Circle.dat within gnuplot, without having to write a new
program. Note that
. We can do that using
the raw data from the file Circle.dat within gnuplot, without having to write a new
program. Note that  . The function atan2 is available in
gnuplot
as well as in Fortran. Use the online help system in gnuplot in order to see its
usage:
. The function atan2 is available in
gnuplot
as well as in Fortran. Use the online help system in gnuplot in order to see its
usage:
gnuplot> help atan2
The ‘atan2(y,x)‘ function returns the arc tangent (inverse
tangent) of the ratio of the real parts of its arguments.
‘atan2‘ returns its argument in radians or degrees, as
selected by ‘set angles‘, in the correct quadrant.
Therefore, the right way to call the function is atan2(y-y0,x-x0). In our case
x0=y0=1 and x, y are in the 2nd and 3rd columns of the file Circle.dat.
We can construct an expression after the using command as in page
153, where $2 is the value of the second and $3 the value of the third
column:
gnuplot> x0 = 1 ; y0 = 1
gnuplot> plot "Circle.dat" using 1:(atan2($3-y0,$2-x0)) \
with lines title "theta(t)",pi,-pi
The second command is broken in two lines by using the character ∖ so that it fits conveniently
in the text .
Note how we defined the values of the variables x0, y0 and how we used them in the
expression atan2($3-x0,$2-y0). We also plot the lines which graph the constant
functions  and
and  which mark the limit values of
which mark the limit values of  . The gnuplot
variable
pi is predefined and can be used in formed expressions. The result can be seen in
the left plot of figure 2.4.
. The gnuplot
variable
pi is predefined and can be used in formed expressions. The result can be seen in
the left plot of figure 2.4.
The velocity components  as function of time as well as the
trajectory
as function of time as well as the
trajectory  can be plotted with the commands:
can be plotted with the commands:
gnuplot> plot "Circle.dat" using 1:4 title "v_x(t)" \
with lines
gnuplot> replot "Circle.dat" using 1:5 title "v_y(t)" \
with lines
gnuplot> plot "Circle.dat" using 2:3 title "x-y"
with lines
We close this section by showing how to do a simple animation of
the particle trajectory using gnuplot. There is a file animate2D.gnu in
the accompanied software which you can copy in the directory where
you have the data file Circle.dat. We are not going to explain how it
works
but how to use it in order to make your own animations. The final result
is shown in figure 2.5. All that you need to do is to define the data
file ,
the initial time t0, the final time tf and the time step dt. These times can be
different from the ones we used to create the data in Circle.dat. A full
animation session can be launched using the commands:
gnuplot> file = "Circle.dat"
gnuplot> set xrange [0:1.6]; set yrange [0:1.6]
gnuplot> t0 = 0; tf = 20 ; dt = 0.1
gnuplot> load "animate2D.gnu"
The first line defines the data file that animate2D.gnu reads data from. The
second line sets the range of the plots and the third line defines the time
parameters used in the animation. The final line launches the animation. If you
want to rerun the animation, you can repeat the last two commands as many
times as you want using the same or different parameters. E.g. if you wish to run
the animation at “half the speed” you should simply redefine dt=0.05 and set the
initial time to t0=0:
gnuplot> t0 = 0; dt = 0.05
gnuplot> load "animate2D.gnu"
2.1.2 More Examples
We are now going to apply the steps described in the previous section to
other examples of motion on the plane. The first problem that we are
going to discuss is that of the small oscillations of a simple pendulum.
Figure 2.6 shows the single oscillating degree of freedom  , which
is the small angle that the pendulum forms with the vertical direction.
, which
is the small angle that the pendulum forms with the vertical direction.
The motion is periodic with angular frequency  and period
and period
 . The angular velocity is computed from
. The angular velocity is computed from  which gives
which gives
We have chosen the initial conditions  and
and  . In order to
write the equations of motion in the Cartesian coordinate system shown in figure
2.6 we use the relations These are similar to the equations (2.3) and (2.4) that we used in the case of
the circular motion of the previous section. Therefore the structure of the
program is quite similar. Its final form, which can be found in the file
SimplePendulum.f90, is:
. In order to
write the equations of motion in the Cartesian coordinate system shown in figure
2.6 we use the relations These are similar to the equations (2.3) and (2.4) that we used in the case of
the circular motion of the previous section. Therefore the structure of the
program is quite similar. Its final form, which can be found in the file
SimplePendulum.f90, is:
!==============================================================
!File SimplePendulum.f90
!Set pendulum original position at theta0 with no initial speed
!--------------------------------------------------------------
program SimplePendulum
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: l,x,y,vx,vy,t,t0,tf,dt
real :: theta,theta0,dtheta_dt,omega
real, parameter ::PI=3.1415927,g=9.81
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter l: ’
read *,l
print *,’# Enter theta0:’
read *,theta0
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# l= ’,l ,’ theta0= ’,theta0
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
omega = sqrt(g/l)
print *,’# omega= ’,omega,’ T= ’,2.0*PI/omega
open(unit=11,file=’SimplePendulum.dat’)
!------------------------------------------------------------
!Compute:
t = t0
do while(t .le. tf)
theta = theta0*cos(omega*(t-t0))
dtheta_dt = -omega*theta0*sin(omega*(t-t0))
x = l*sin(theta)
y = -l*cos(theta)
vx = l*dtheta_dt*cos(theta)
vy = l*dtheta_dt*sin(theta)
write(11,100)t,x,y,vx,vy,theta,dtheta_dt
t = t + dt
enddo
close(11)
100 FORMAT(7G15.7)
end program SimplePendulum
We note that the acceleration of gravity  is hard coded in the program and
that the user can only set the length
is hard coded in the program and
that the user can only set the length  of the pendulum. The data file
SimplePendulum.dat produced by the program, contains two extra columns with
the current values of
of the pendulum. The data file
SimplePendulum.dat produced by the program, contains two extra columns with
the current values of  and the angular velocity
and the angular velocity  . The statement
write(11,100) writes to the unit 11 according to the format set by the FORMAT
statement, found in the line labeled by the label 100. This is done so that we can
be sure that the data is printed in one line for each value of
. The statement
write(11,100) writes to the unit 11 according to the format set by the FORMAT
statement, found in the line labeled by the label 100. This is done so that we can
be sure that the data is printed in one line for each value of  (see the discussion
on page 119).
(see the discussion
on page 119).
A simple session for the study of the above problem is shown
below :
> gfortran SimplePendulum.f90 -o sp
> ./sp
# Enter l:
1.0
# Enter theta0:
0.314
# Enter t0,tf,dt:
0 20 0.01
# l= 1. theta0= 0.31400001
# t0= 0. tf= 20. dt= 0.00999999978
# omega= 3.132092 T= 2.0060668
> gnuplot
gnuplot> plot "SimplePendulum.dat" u 1:2 w l t "x(t)"
gnuplot> plot "SimplePendulum.dat" u 1:3 w l t "y(t)"
gnuplot> plot "SimplePendulum.dat" u 1:4 w l t "v_x(t)"
gnuplot> replot "SimplePendulum.dat" u 1:5 w l t "v_y(t)"
gnuplot> plot "SimplePendulum.dat" u 1:6 w l t "theta(t)"
gnuplot> replot "SimplePendulum.dat" u 1:7 w l t "theta’(t)"
gnuplot> plot [-0.6:0.6][-1.1:0.1] "SimplePendulum.dat" \
u 2:3 w l t "x-y"
gnuplot> file = "SimplePendulum.dat"
gnuplot> t0=0;tf=20.0;dt=0.1
gnuplot> set xrange [-0.6:0.6];set yrange [-1.1:0.1]
gnuplot> load "animate2D.gnu"
The next example is the study of the trajectory of a particle shot near the earth’s
surface
when we consider the effect of air resistance to be negligible. Then, the equations
describing the trajectory of the particle and its velocity are given by the
parametric equations
where  is the parameter. The initial conditions are
is the parameter. The initial conditions are  ,
,
 and
and  , as shown in figure 2.7.
, as shown in figure 2.7.
The structure of the program is similar to the previous ones. The user enters
the magnitude of the particle’s initial velocity and the shooting angle  in
degrees. The initial time is taken to be
in
degrees. The initial time is taken to be  . The program calculates
. The program calculates  and
and  and prints them to the stdout. The data is written to the file
Projectile.dat. The full program is listed below and it can be found in the file
Projectile.f90 in the accompanied software:
and prints them to the stdout. The data is written to the file
Projectile.dat. The full program is listed below and it can be found in the file
Projectile.f90 in the accompanied software:
!============================================================
!File Projectile.f90
!Shooting a projectile near the earth surface.
!No air resistance.
!Starts at (0,0), set (v0,theta).
!------------------------------------------------------------
program Projectile
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: x0,y0,R,x,y,vx,vy,t,tf,dt
real :: theta,v0x,v0y,v0
real, parameter :: PI=3.1415927,g=9.81
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter v0,theta (in degrees):’
read *,v0,theta
print *,’# Enter tf,dt:’
read *, tf,dt
print *,’# v0= ’,v0,’ theta= ’,theta,’o (degrees)’
print *,’# t0= ’,0.0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
if( v0 .le. 0.0) stop ’Illegal value of v0<=0’
if( theta .le. 0.0 .or. theta .ge. 90.0) &
stop ’Illegal value of theta’
theta = (PI/180.0)*theta !convert to radians
v0x = v0*cos(theta)
v0y = v0*sin(theta)
print *,’# v0x = ’,v0x,’ v0y= ’,v0y
open(unit=11,file=’Projectile.dat’)
!------------------------------------------------------------
!Compute:
t = 0.0
do while(t .le. tf)
x = v0x * t
y = v0y * t - 0.5*g*t*t
vx = v0x
vy = v0y - g*t
write(11,*)t,x,y,vx,vy
t = t + dt
enddo
close(11)
end program Projectile
A typical session for the study of this problem is shown below:
> gfortran Projectile.f90 -o pj
> ./pj
# Enter v0,theta (in degrees):
10 45
# Enter tf,dt:
1.4416 0.001
# v0= 10.0000000 theta= 45.000000 o (degrees)
# t0= 0.0000000 tf= 1.4416000 dt= 1.00000005E-03
# v0x = 7.0710678 v0y= 7.0710678
> gnuplot
gnuplot> plot "Projectile.dat" using 1:2 w l t "x(t)"
gnuplot> replot "Projectile.dat" using 1:3 w l t "y(t)"
gnuplot> plot "Projectile.dat" using 1:4 w l t "v_x(t)"
gnuplot> replot "Projectile.dat" using 1:5 w l t "v_y(t)"
gnuplot> plot "Projectile.dat" using 2:3 w l t "x-y"
gnuplot> file = "Projectile.dat"
gnuplot> set xrange [0:10.3];set yrange [0:10.3]
gnuplot> t0=0;tf=1.4416;dt=0.05
gnuplot> load "animate2D.gnu"
Next, we will study the effect of air resistance of the form  . The
solutions to the equations of motion
. The
solutions to the equations of motion
with initial conditions  ,
,  and
and  are
are
Programming the above equations is as easy as before, the only difference
being that the user needs to provide the value of the constant  . The full
program can be found in the file ProjectileAirResistance.f90 and it is listed
below:
. The full
program can be found in the file ProjectileAirResistance.f90 and it is listed
below:
!============================================================
!File ProjectileAirResistance.f90
!Shooting a projectile near the earth surface
!with air resistance
!Starts at (0,0), set k, (v0,theta).
!------------------------------------------------------------
program ProjectileAirResistance
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: x0,y0,R,x,y,vx,vy,t,tf,dt,k
real :: theta,v0x,v0y,v0
real, parameter :: PI=3.1415927,g=9.81
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter k, v0,theta (in degrees):’
read *,k, v0,theta
print *,’# Enter tf,dt:’
read *, tf,dt
print *,’# k = ’,k
print *,’# v0= ’,v0,’ theta= ’,theta,’o (degrees)’
print *,’# t0= ’,0.0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
if( v0 .le. 0.0) stop ’Illegal value of v0<=0’
if( k .le. 0.0) stop ’Illegal value of k <=0’
if( theta .le. 0.0 .or. theta .ge. 90.0) &
stop ’Illegal value of theta’
theta = (PI/180.0)*theta !convert to radians
v0x = v0*cos(theta)
v0y = v0*sin(theta)
print *,’# v0x = ’,v0x,’ v0y= ’,v0y
open(unit=11,file=’ProjectileAirResistance.dat’)
!------------------------------------------------------------
!Compute:
t = 0.0
do while(t .le. tf)
x = (v0x/k)*(1.0-exp(-k*t))
y = (1.0/k)*(v0y+(g/k))*(1.0-exp(-k*t))-(g/k)*t
vx = v0x*exp(-k*t)
vy = (v0y+(g/k))*exp(-k*t)-(g/k)
write(11,*)t,x,y,vx,vy
t = t + dt
enddo
close(11)
end program ProjectileAirResistance
We also list the commands of a typical session of the study of the
problem:
> gfortran ProjectileAirResistance.f90 -o pja
> ./pja
# Enter k, v0,theta (in degrees):
5.0 10.0 45
# Enter tf,dt:
0.91 0.001
# k = 5.
# v0= 10. theta= 45.o (degrees)
# t0= 0. tf= 0.910000026 dt= 0.00100000005
# v0x = 7.07106781 v0y= 7.07106781
> gnuplot
gnuplot> v0x = 10*cos(pi/4) ; v0y = 10*sin(pi/4)
gnuplot> g = 9.81 ; k = 5
gnuplot> plot [:][:v0x/k+0.1] "ProjectileAirResistance.dat" \
using 1:2 with lines title "x(t)",v0x/k
gnuplot> replot "ProjectileAirResistance.dat" \
using 1:3 with lines title "y(t)",\
-(g/k)*x+(g/k**2)+v0y/k
gnuplot> plot [:][-g/k-0.6:] "ProjectileAirResistance.dat" \
using 1:4 with lines title "v_x(t)",0
gnuplot> replot "ProjectileAirResistance.dat" \
using 1:5 with lines title "v_y(t)",-g/k
gnuplot> plot "ProjectileAirResistance.dat" \
using 2:3 with lines title "With air resistance k=5.0"
gnuplot> replot "Projectile.dat" \
using 2:3 with lines title "No air resistance k=0.0"
gnuplot> file = "ProjectileAirResistance.dat"
gnuplot> set xrange [0:1.4];set yrange [0:1.4]
gnuplot> t0=0;tf=0.91;dt=0.01
gnuplot> load "animate2D.gnu"
Long commands have been continued to the next line as before. We defined the
gnuplot variables v0x, v0y, g and k to have the values that we used when
running the program. We can use them in order to construct the asymptotes of
the plotted functions of time. The results are shown in figures 2.9 and
2.10.
The last example of this section will be that of the anisotropic harmonic
oscillator. The force on the particle is
 | (2.11) |
where the “spring constants”  and
and  are different in the
directions of the axes
are different in the
directions of the axes  and
and  . The solutions of the dynamical equations
of motion for
. The solutions of the dynamical equations
of motion for  ,
,  ,
,  and
and  are
are
If the angular frequencies  and
and  satisfy certain relations, the trajectories of
the particle are closed and self intersect at a given number of points.
The proof of these relations, as well as their numerical confirmation, is
left as an exercise for the reader. The program listed below is in the file
Lissajoux.f90:
satisfy certain relations, the trajectories of
the particle are closed and self intersect at a given number of points.
The proof of these relations, as well as their numerical confirmation, is
left as an exercise for the reader. The program listed below is in the file
Lissajoux.f90:
!============================================================
!File Lissajous.f90
!Lissajous curves (special case)
!x(t)= cos(o1 t), y(t)= sin(o2 t)
!------------------------------------------------------------
program Lissajous
implicit none
!------------------------------------------------------------
!Declaration of variables
real x0,y0,R,x,y,vx,vy,t,t0,tf,dt
real o1,o2,T1,T2
real, parameter :: PI=3.1415927
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter omega1 and omega2:’
read *,o1,o2
print *,’# Enter tf,dt:’
read *,tf,dt
print *,’# o1= ’,o1, ’ o2= ’,o2
print *,’# t0= ’,0.0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
if(o1.le.0.0 .or. o2.le.0.0) stop ’omega1 or omega2<=0’
T1 = 2.0*PI/o1
T2 = 2.0*PI/o2
print *,’# T1= ’,T1,’ T2= ’,T2
open(unit=11,file=’Lissajous.dat’)
!------------------------------------------------------------
!Compute:
t = 0.0
do while(t .le. tf)
x = cos(o1*t)
y = sin(o2*t)
vx = -o1*sin(o1*t)
vy = o2*cos(o2*t)
write(11,*)t,x,y,vx,vy
t = t + dt
enddo
close(11)
end program Lissajous
We have set  in the program above. The user must enter the two angular
frequencies
in the program above. The user must enter the two angular
frequencies  and
and  and the corresponding times. A typical session for the
study of the problem is shown below:
and the corresponding times. A typical session for the
study of the problem is shown below:
> gfortran Lissajous.f90 -o lsj
> ./lsj
# Enter omega1 and omega2:
3 5
# Enter tf,dt:
10.0 0.01
# o1= 3. o2= 5.
# t0= 0. tf= 10. dt= 0.00999999978
# T1= 2.09439516 T2= 1.2566371
>gnuplot
gnuplot> plot "Lissajous.dat" using 1:2 w l t "x(t)"
gnuplot> replot "Lissajous.dat" using 1:3 w l t "y(t)"
gnuplot> plot "Lissajous.dat" using 1:4 w l t "v_x(t)"
gnuplot> replot "Lissajous.dat" using 1:5 w l t "v_y(t)"
gnuplot> plot "Lissajous.dat" using 2:3 w l t "x-y for 3:5"
gnuplot> file = "Lissajous.dat"
gnuplot> set xrange [-1.1:1.1];set yrange [-1.1:1.1]
gnuplot> t0=0;tf=10;dt=0.1
gnuplot> load "animate2D.gnu"
The results for  and
and  are shown in figure 2.11.
are shown in figure 2.11.
2.2 Motion in Space
By slightly generalizing the methods described in the previous section, we will
study the motion of a particle in three dimensional space. All we have to do is to
add an extra equation for the coordinate  and the component of the
velocity
and the component of the
velocity  . The structure of the programs will be exactly the same as
before.
. The structure of the programs will be exactly the same as
before.
The first example is the conical pendulum, which can be seen in figure 2.12.
The particle moves on the  plane with constant angular velocity
plane with constant angular velocity  . The
equations of motion are derived from the relations
. The
equations of motion are derived from the relations
 | (2.13) |
where  . Their solution
is
. Their solution
is
where we have to substitute the values For the velocity components we obtain Therefore we must have
 | (2.17) |
and when  ,
,  .
.
In the program that we will write, the user must enter the parameters  ,
,  ,
the final time
,
the final time  and the time step
and the time step  . We take
. We take  . The convention that
we follow for the output of the results is that they should be written in a file
where the first 7 columns are the values of
. The convention that
we follow for the output of the results is that they should be written in a file
where the first 7 columns are the values of  ,
,  ,
,  ,
,  ,
,  ,
,  and
and
 . Each line in this file is long and, in order to prevent Fortran from
breaking it into two separate lines, we have to give an explicit format
specification. See the discussion on page 119. The full program is listed
below:
. Each line in this file is long and, in order to prevent Fortran from
breaking it into two separate lines, we have to give an explicit format
specification. See the discussion on page 119. The full program is listed
below:
!============================================================
!File ConicalPendulum.f90
!Set pendulum angular velocity omega and display motion in 3D
!------------------------------------------------------------
program ConicalPendulum
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: l,r,x,y,z,vx,vy,vz,t,tf,dt
real :: theta,cos_theta,sin_theta,omega
real, parameter :: PI=3.1415927,g=9.81
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter l,omega: ’
read *,l,omega
print *,’# Enter tf,dt:’
read *,tf,dt
print *,’# l= ’,l ,’ omega= ’,omega
print *,’# T= ’,2.0*PI/omega,’ omega_min= ’,sqrt(g/l)
print *,’# t0= ’,0.0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
cos_theta = g/(omega*omega*l)
if( cos_theta .ge. 1) stop ’cos(theta)>= 1’
sin_theta = sqrt(1.0-cos_theta*cos_theta)
z = -g/(omega*omega) !they remain constant throught
vz= 0.0 !the motion
r = g/(omega*omega)*sin_theta/cos_theta
open(unit=11,file=’ConicalPendulum.dat’)
!------------------------------------------------------------
!Compute:
t = 0.0
do while(t .le. tf)
x = r*cos(omega*t)
y = r*sin(omega*t)
vx = -r*sin(omega*t)*omega
vy = r*cos(omega*t)*omega
write(11,100)t,x,y,z,vx,vy,vz
t = t + dt
enddo
close(11)
100 FORMAT(20G15.7)
end program ConicalPendulum
In order to compile and run the program we can use the commands shown
below:
> gfortran ConicalPendulum.f90 -o cpd
> ./cpd
# Enter l,omega:
1.0 6.28
# Enter tf,dt:
10.0 0.01
# l= 1. omega= 6.28000021
# T= 1.00050724 omega_min= 3.132092
# t0= 0. tf= 10. dt= 0.00999999978
The results are recorded in the file ConicalPendulum.dat. In order to plot the
functions  ,
,  ,
,  ,
,  ,
,  ,
,  we give the following gnuplot
commands:
we give the following gnuplot
commands:
> gnuplot
gnuplot> plot "ConicalPendulum.dat" u 1:2 w l t "x(t)"
gnuplot> replot "ConicalPendulum.dat" u 1:3 w l t "y(t)"
gnuplot> replot "ConicalPendulum.dat" u 1:4 w l t "z(t)"
gnuplot> plot "ConicalPendulum.dat" u 1:5 w l t "v_x(t)"
gnuplot> replot "ConicalPendulum.dat" u 1:6 w l t "v_y(t)"
gnuplot> replot "ConicalPendulum.dat" u 1:7 w l t "v_z(t)"
The results are shown in figure 2.13.
In order to make a three dimensional plot of the trajectory, we should use the
gnuplot command splot:
gnuplot> splot "ConicalPendulum.dat" u 2:3:4 w l t "r(t)"
The result is shown in figure 2.14. We can click on the trajectory and rotate it
and view it from a different angle. We can change the plot limits with the
command:
gnuplot> splot [-1.1:1.1][-1.1:1.1][-0.3:0.0] \
"ConicalPendulum.dat" using 2:3:4 w l t "r(t)"
We can animate the trajectory of the particle by using the file animate3D.gnu
from the accompanying software. The commands are similar to the ones we had to
give in the two dimensional case for the planar trajectories when we used the file
animate2D.gnu:
gnuplot> file = "ConicalPendulum.dat"
gnuplot> set xrange [-1.1:1.1];set yrange [-1.1:1.1]
gnuplot> set zrange [-0.3:0]
gnuplot> t0=0;tf=10;dt=0.1
gnuplot> load "animate3D.gnu"
The result can be seen in figure 2.15.
The program animate3D.gnu can be used on the data file of any program that
prints t x y z as the first words on each of its lines. All we have to do is to
change the value of the file variable in gnuplot.
Next, we will study the trajectory of a charged particle in a homogeneous
magnetic field  . At time
. At time  , the particle is at
, the particle is at  and its velocity
is
and its velocity
is  , see figure 2.16.
, see figure 2.16.
The magnetic force on the particle is  and
the equations of motion are
and
the equations of motion are
By integrating the above equations with the given initial conditions we obtain
Integrating once more, we obtain the position of the particle as a function of time
where we have chosen  . This choice places the center of the circle,
which is the projection of the trajectory on the
. This choice places the center of the circle,
which is the projection of the trajectory on the  plane, to be at the origin of
the coordinate system. The trajectory is a helix with radius
plane, to be at the origin of
the coordinate system. The trajectory is a helix with radius  and pitch
and pitch
 .
.
We are now ready to write a program that calculates the trajectory given by
(2.20) . The user enters the parameters  and
and  , shown in figure 2.16, as well
as the angular frequency
, shown in figure 2.16, as well
as the angular frequency  (Larmor frequency). The components of the initial
velocity are
(Larmor frequency). The components of the initial
velocity are  and
and  . The initial position is calculated
from the equation
. The initial position is calculated
from the equation  . The program can be found in the file
ChargeInB.f90:
. The program can be found in the file
ChargeInB.f90:
!===========================================================
!File ChargeInB.f90
!A charged particle of mass m and charge q enters a magnetic
!field B in +z direction. It enters with velocity
!v0x=0,v0y=v0 cos(theta),v0z=v0 sin(theta), 0<=theta<pi/2
!at the position x0=-v0y/omega, omega=q B/m
!
!Enter v0 and theta and see trajectory from
!t0=0 to tf at step dt
!------------------------------------------------------------
program ChargeInB
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: x,y,z,vx,vy,vz,t,tf,dt
real :: x0,y0,z0,v0x,v0y,v0z,v0
real :: theta,omega
real, parameter :: PI=3.1415927
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter omega: ’
read *,omega
print *,’# Enter v0, theta (degrees):’
read *,v0,theta
print *,’# Enter tf,dt:’
read *,tf,dt
print *,’# omega= ’,omega ,’ T= ’,2.0*PI/omega
print *,’# v0= ’,v0, ’ theta= ’,theta,’o (degrees)’
print *,’# t0= ’,0.0, ’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
if(theta.lt.0.0 .or. theta.ge.90.0)stop ’Illegal 0<theta<90’
theta = (PI/180.0)*theta !convert to radians
v0y = v0*cos(theta)
v0z = v0*sin(theta)
print *,’# v0x= ’,0.0,’ v0y= ’,v0y,’ v0z= ’,v0z
x0 = - v0y/omega
print *,’# x0= ’,x0, ’ y0= ’,0.0,’ z0= ’,0.0
print *,’# xy plane: Circle with center (0,0) and R= ’,ABS(x0)
print *,’# step of helix: s=v0z*T= ’,v0z*2.0*PI/omega
open(unit=11,file=’ChargeInB.dat’)
!------------------------------------------------------------
!Compute:
t = 0.0
vz = v0z
do while(t .le. tf)
x = x0*cos(omega*t)
y = -x0*sin(omega*t)
z = v0z*t
vx = v0y*sin(omega*t)
vy = v0y*cos(omega*t)
write(11,100)t,x,y,z,vx,vy,vz
t = t + dt
enddo
close(11)
100 FORMAT(20G15.7)
end program ChargeInB
A typical session in which we calculate the trajectories shown in figures 2.17 and
2.18 is shown below:
> gfortran ChargeInB.f90 -o chg
> ./chg
# Enter omega:
6.28
# Enter v0, theta (degrees):
1.0 20
# Enter tf,dt:
10 0.01
# omega= 6.28000021 T= 1.00050724
# v0= 1. theta= 20.o (degrees)
# t0= 0. tf= 10. dt= 0.00999999978
# v0x= 0. v0y= 0.939692616 v0z= 0.342020124
# x0= -0.149632573 y0= 0. z0= 0.
# xy plane: Circle with center (0,0) and R= 0.149632573
# step of helix: s=v0z*T= 0.342193604
> gnuplot
gnuplot> plot "ChargeInB.dat" u 1:2 w l title "x(t)"
gnuplot> replot "ChargeInB.dat" u 1:3 w l title "y(t)"
gnuplot> replot "ChargeInB.dat" u 1:4 w l title "z(t)"
gnuplot> plot "ChargeInB.dat" u 1:5 w l title "v_x(t)"
gnuplot> replot "ChargeInB.dat" u 1:6 w l title "v_y(t)"
gnuplot> replot "ChargeInB.dat" u 1:7 w l title "v_z(t)"
gnuplot> splot "ChargeInB.dat" u 2:3:4 w l title "r(t)"
gnuplot> file = "ChargeInB.dat"
gnuplot> set xrange [-0.65:0.65];set yrange [-0.65:0.65]
gnuplot> set zrange [0:1.3]
gnuplot> t0=0;tf=3.5;dt=0.1
gnuplot> load "animate3D.gnu"
2.3 Trapped in a Box
In this section we will study the motion of a particle that is free, except when
bouncing elastically on a wall or on certain obstacles. This motion is calculated by
approximate algorithms that introduce systematic errors. These types of
errors
are also encountered in the study of more complicated dynamics, but the
simplicity of the problem will allow us to control them in a systematic and easy to
understand way.
2.3.1 The One Dimensional Box
The simplest example of such a motion is that of a particle in a “one
dimensional box”. The particle moves freely on the  axis for
axis for  , as
can be seen in figure 2.19. When it reaches the boundaries
, as
can be seen in figure 2.19. When it reaches the boundaries  and
and
 it bounces and its velocity instantly reversed. Its potential energy
is
it bounces and its velocity instantly reversed. Its potential energy
is
 | (2.21) |
which has the shape of an infinitely deep well. The force  within the box and
within the box and  at the position of the walls.
at the position of the walls.
Initially we have to know the position of the particle  as well as its velocity
as well as its velocity
 (the sign of
(the sign of  depends on the direction of the particle’s motion) at time
depends on the direction of the particle’s motion) at time
 . As long as the particle moves within the box, its motion is free and
. As long as the particle moves within the box, its motion is free and
For a small enough change in time  , so that there is no bouncing on the wall in
the time interval
, so that there is no bouncing on the wall in
the time interval  , we have that Therefore we could use the above relations in our program and when the particle
bounces off a wall we could simple reverse its velocity
, we have that Therefore we could use the above relations in our program and when the particle
bounces off a wall we could simple reverse its velocity  . The devil is
hiding in the word “when”. Since the time interval
. The devil is
hiding in the word “when”. Since the time interval  is finite in our program,
there is no way to know the instant of the collision with accuracy better than
is finite in our program,
there is no way to know the instant of the collision with accuracy better than
 . However, our algorithm will change the direction of the velocity
at time
. However, our algorithm will change the direction of the velocity
at time  , when the particle will have already crossed the wall.
This will introduce a systematic error, which is expected to decrease with
decreasing
, when the particle will have already crossed the wall.
This will introduce a systematic error, which is expected to decrease with
decreasing  . One way to implement the above idea is by constructing the
loop
. One way to implement the above idea is by constructing the
loop
do while(t .le. tf)
write(11,*)t,x,v
x = x + v*dt
t = t + dt
if(x .lt. 0.0 .or. x .gt. L) v = -v
enddo
where the last line gives the testing condition for the wall collision and the
subsequent change of the velocity.
The full program that realizes the proposed algorithm is listed below and can
be found in the file box1D_1.f90. The user can set the size of the box L, the
initial conditions x0 and v0 at time t0, the final time tf and the time step
dt:
!============================================================
!File box1D_1.f90
!Motion of a free particle in a box 0<x<L
!Use integration with time step dt: x = x + v*dt
!------------------------------------------------------------
program box1D
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: L,x0,v0,t0,tf,dt,t,x,v
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter L:’
read *,L
print *,’# L = ’,L
if( L .le. 0.0) stop ’L must be positive.’
print *,’# Enter x0,v0:’
read *,x0,v0
print *,’# x0= ’,x0,’ v0= ’,v0
if(x0 .lt. 0.0 .or. x0 .gt. L) stop ’illegal value of x0.’
if(v0 .eq. 0.0 ) stop ’illegal value of v0 = 0.’
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
t = t0
x = x0
v = v0
open(unit=11,file=’box1D_1.dat’)
!------------------------------------------------------------
!Compute:
do while(t .le. tf)
write(11,*)t,x,v
x = x + v*dt
t = t + dt
if(x .lt. 0.0 .or. x .gt. L) v = -v
enddo
close(11)
end program box1D
The computed data is recorded in the file box1D_1.dat in three columns.
Compiling, running and plotting the trajectory using gnuplot can be done as
follows:
> gfortran box1D_1.f90 -o box1
> ./box1
# Enter L:
10
# L = 10.
# Enter x0,v0:
0 1.0
# x0= 0. v0= 1.
# Enter t0,tf,dt:
0 100 0.01
# t0= 0. tf= 100. dt= 0.00999999978
> gnuplot
gnuplot> plot "box1D_1.dat" using 1:2 w l title "x(t)",\
0 notitle,10 notitle
gnuplot> plot [:][-1.2:1.2] "box1D_1.dat" \
using 1:3 w l title "v(t)"
The trajectory  is shown in figure 2.20. The effects of the systematic
errors can be easily seen by noting that the expected collisions occur every
is shown in figure 2.20. The effects of the systematic
errors can be easily seen by noting that the expected collisions occur every
 units of time. Therefore, on the plot to the right of figure 2.20,
the reversal of the particle’s motion should have occurred at
units of time. Therefore, on the plot to the right of figure 2.20,
the reversal of the particle’s motion should have occurred at  ,
,
 .
.
The reader should have already realized that the above mentioned error can be
made to vanish by taking arbitrarily small  . Therefore, we naively expect that
as long as we have the necessary computer power to take
. Therefore, we naively expect that
as long as we have the necessary computer power to take  as small as possible
and the corresponding time intervals as many as possible, we can achieve any
precision that we want. Well, that is true only up to a point. The problem is that
the next position is determined by the addition operation x+v*dt and
the next moment in time by t+dt. Floating point numbers of the REAL
type have a maximum accuracy of approximately 7 significant decimal
digits. Therefore, if the operands x and v*dt are real numbers differing
by more than 7 orders of magnitude (v*dt
as small as possible
and the corresponding time intervals as many as possible, we can achieve any
precision that we want. Well, that is true only up to a point. The problem is that
the next position is determined by the addition operation x+v*dt and
the next moment in time by t+dt. Floating point numbers of the REAL
type have a maximum accuracy of approximately 7 significant decimal
digits. Therefore, if the operands x and v*dt are real numbers differing
by more than 7 orders of magnitude (v*dt x), the effect of the
addition x+v*dt=x, which is null! The reason is that the floating point
unit of the processor has to convert both numbers x and v*dt into a
representation having the same exponent and in doing so, the corresponding
significant digits of the smaller number v*dt are lost. The result is less
catastrophic when v*dt
x), the effect of the
addition x+v*dt=x, which is null! The reason is that the floating point
unit of the processor has to convert both numbers x and v*dt into a
representation having the same exponent and in doing so, the corresponding
significant digits of the smaller number v*dt are lost. The result is less
catastrophic when v*dt x with
x with  , but some degree
of accuracy is also lost at each addition operation. And since we have
accumulation of such errors over many intervals t
, but some degree
of accuracy is also lost at each addition operation. And since we have
accumulation of such errors over many intervals t t+dt, the error can
become significant and destroy our calculation for large enough times.
A similar error accumulates in the determination of the next instant of
time t+dt, but we will discuss below how to make this contribution to
the total error negligible. The above mentioned errors can become less
detrimental by using floating point numbers of greater accuracy than the REAL
type. For example REAL(8) numbers have approximately 16 significant
decimal digits. But again, the precision is finite and the same type of
errors are there only to be revealed by a more demanding and complicated
calculation.
t+dt, the error can
become significant and destroy our calculation for large enough times.
A similar error accumulates in the determination of the next instant of
time t+dt, but we will discuss below how to make this contribution to
the total error negligible. The above mentioned errors can become less
detrimental by using floating point numbers of greater accuracy than the REAL
type. For example REAL(8) numbers have approximately 16 significant
decimal digits. But again, the precision is finite and the same type of
errors are there only to be revealed by a more demanding and complicated
calculation.
The remedy to such a problem can only be a change in the algorithm. This
is not always possible, but in the case at hand this is easy to do. For
example, consider the equation that gives the position of a particle in free
motion
 | (2.24) |
Let’s use the above relation for the parts of the motion between two collisions.
Then, all we have to do is to reverse the direction of the motion and reset the
initial position and time to be the position and time of the collision. This can be
done by using the loop:
t = t0
do while(t .le. tf)
x = x0 + v0*(t-t0)
write(11,*)t,x,v0
if( x .lt. 0.0 .or. x .gt. L)then
x0 = x
t0 = t
v0 = -v0
endif
t = t + dt
In the above algorithm, the error in the time of the collision is not
vanishing but we don’t have the “instability” problem of the dt limit .
Therefore we can isolate and study the effect of each type of error. The full
program that implements the above algorithm is given below and can be found in
the file box1D_2.f90:
limit .
Therefore we can isolate and study the effect of each type of error. The full
program that implements the above algorithm is given below and can be found in
the file box1D_2.f90:
!============================================================
!File box1D_2.f90
!Motion of a free particle in a box 0<x<L
!Use constant velocity equation: x = x0 + v0*(t-t0)
!Reverse velocity and redefine x0,t0 on boundaries
!------------------------------------------------------------
program box1D
implicit none
!------------------------------------------------------------
!Declaration of variables
real :: L,x0,v0,t0,tf,dt,t,x,v
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter L:’
read *,L
print *,’# L = ’,L
if( L .le. 0.0) stop ’L must be positive.’
print *,’# Enter x0,v0:’
read *,x0,v0
print *,’# x0= ’,x0,’ v0= ’,v0
if(x0 .lt. 0.0 .or. x0 .gt. L) stop ’illegal value of x0.’
if(v0 .eq. 0.0 ) stop ’illegal value of v0 = 0.’
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
t = t0
open(unit=11,file=’box1D_2.dat’)
!------------------------------------------------------------
!Compute:
do while(t .le. tf)
x = x0 + v0*(t-t0)
write(11,*)t,x,v0
if( x .lt. 0.0 .or. x .gt. L)then
x0 = x
t0 = t
v0 = -v0
endif
t = t + dt
enddo
close(11)
end program box1D
Compiling and running the above program is done as before and the results
are stored in the file box1D_2.dat. The algorithm can be improved in
order to compute the exact solution. We leave that as an exercise for the
reader .
2.3.2 Errors
In this section we will study the effect of the systematic errors that we
encountered in the previous section in more detail. We considered two types of
errors: First, the systematic error of determining the instant of the collision of the
particle with the wall. This error is reduced by taking a smaller time step  .
Then, the systematic error that accumulates with each addition of two numbers
with increasing difference in their orders of magnitude. This error is increased
with decreasing
.
Then, the systematic error that accumulates with each addition of two numbers
with increasing difference in their orders of magnitude. This error is increased
with decreasing  . The competition of the two effects makes the optimal choice
of
. The competition of the two effects makes the optimal choice
of  the result of a careful analysis. Such a situation is found in many
interesting problems, therefore it is quite instructive to study it in more
detail.
the result of a careful analysis. Such a situation is found in many
interesting problems, therefore it is quite instructive to study it in more
detail.
When the exact solution of the problem is not known, the systematic errors
are controlled by studying the behavior of the solution as a function of  . If the
solutions are converging in a region of values of
. If the
solutions are converging in a region of values of  , one gains confidence
that the true solution has been determined up to the accuracy of the
convergence.
, one gains confidence
that the true solution has been determined up to the accuracy of the
convergence.
In the previous sections, we studied two different algorithms, programmed in
the files box1D_1.f90 and box1D_2.f90. We will refer to them as “method
1” and “method 2” respectively. We will study the convergence of the
results as  by fixing all the parameters except
by fixing all the parameters except  and then study
the dependence of the results on
and then study
the dependence of the results on  . We will take
. We will take  ,
,  ,
,
 ,
,  ,
,  , so that the particle will collide with the
wall every 10 units of time. We will measure the position of the particle
, so that the particle will collide with the
wall every 10 units of time. We will measure the position of the particle
 as a function of
as a function of  and study its convergence to a
limit
as
and study its convergence to a
limit
as  .
.
The analysis requires a lot of repetitive work: Compiling, setting the
parameter values, running the program and calculating the value of  for
many values of
for
many values of  . We write the values of the parameters read by the program in
a file box1D_anal.in:
. We write the values of the parameters read by the program in
a file box1D_anal.in:
10 L
0 1.0 x0 v0
0 95 0.05 t0 tf dt
Then we compile the program
> gfortran box1D_1.f90 -o box
and run it with the command:
> cat box1D_anal.in | ./box
By using the pipe |, we send the contents of box1D_anal.in to the stdin of the
command ./box by using the command cat. The result  can be found
in the last line of the file box1D_1.dat:
can be found
in the last line of the file box1D_1.dat:
> tail -n 1 box1D_1.dat
94.9511948 5.45000267 -1.
The third number in the above line is the value of the velocity. In a file
box1D_anal.dat we write  and the first two numbers coming out from
the command tail. Then we decrease the value
and the first two numbers coming out from
the command tail. Then we decrease the value  in the file
box1D_anal.in and run again. We repeat for 12 more times until
in the file
box1D_anal.in and run again. We repeat for 12 more times until  reaches the
value
reaches the
value  .
We do the same
using method 2 and we place the results for
.
We do the same
using method 2 and we place the results for  in two new columns in the
file box1D_anal.dat. The result is
in two new columns in the
file box1D_anal.dat. The result is
# ------------------------------------------
# dt t1_95 x1(95) x2(95)
# ------------------------------------------
0.050000 94.95119 5.450003 5.550126
0.025000 94.97849 5.275011 5.174837
0.012500 94.99519 5.124993 5.099736
0.006250 94.99850 4.987460 5.063134
0.003125 94.99734 5.021894 5.035365
0.001563 94.99923 5.034538 5.017764
0.000781 94.99939 4.919035 5.011735
0.000391 94.99979 4.695203 5.005493
0.000195 95.00000 5.434725 5.001935
0.000098 94.99991 5.528124 5.000745
0.000049 94.99998 3.358000 5.000330
0.000024 94.99998 2.724212 5.000232
0.000012 94.99999 9.240705 5.000158
Convergence is studied in figure 2.21. The 1st method maximizes its accuracy
for  , whereas for
, whereas for  the error becomes
the error becomes  % and the
method becomes useless. The 2nd method has much better behavior that the 1st
one.
% and the
method becomes useless. The 2nd method has much better behavior that the 1st
one.
We observe that as  decreases, the final value of
decreases, the final value of  approaches the
expected
approaches the
expected  . Why don’t we obtain
. Why don’t we obtain  , especially when
, especially when  is an
integer? How many steps does it really take to reach
is an
integer? How many steps does it really take to reach  , when the expected
number of those is
, when the expected
number of those is  ? Each time you take a measurement, issue the
command
? Each time you take a measurement, issue the
command
> wc -l box1D_1.dat
which measures the number of lines in the file box1D_1.dat and compare this
number with the expected one. The result is interesting:
# ----------------------
# dt N N0
# ----------------------
0.050000 1900 1900
0.025000 3800 3800
0.012500 7601 7600
0.006250 15203 15200
0.003125 30394 30400
0.001563 60760 60780
0.000781 121751 121638
0.000391 243753 242966
0.000195 485144 487179
0.000098 962662 969387
0.000049 1972589 1938775
0.000024 4067548 3958333
0.000012 7540956 7916666
where the second column has the number of steps computed by the program and
the third one has the expected number of steps. We observe that the accuracy
decreases with decreasing  and in the end the difference is about 5%! Notice
that the last line should have given
and in the end the difference is about 5%! Notice
that the last line should have given  , an error
comparable to the period of the particle’s motion.
, an error
comparable to the period of the particle’s motion.
We conclude that one important source of accumulation of systematic errors is
the calculation of time. This type of errors become more significant with
decreasing  . We can improve the accuracy of the calculation significantly if we
use the multiplication t=t0+i*dt instead of the addition t=t+dt, where i is a
step counter:
. We can improve the accuracy of the calculation significantly if we
use the multiplication t=t0+i*dt instead of the addition t=t+dt, where i is a
step counter:
!t = t + dt ! Not accurate, avoid
t = t0 + i*dt ! Better accuracy, prefer
The main loop in the program box1D_1.f90 becomes:
t = t0
x = x0
v = v0
i = 0
do while(t .le. tf)
write(11,*)t,x,v
i = i + 1
x = x + v*dt
t = t0 + i*dt
if(x .lt. 0.0 .or. x .gt. L) v = -v
enddo
The full program can be found in the file box1D_4.f90 of the accompanying
software. We call this “method 3”. We perform the same change in the file
box1D_2.f90, which we store in the file box1D_5.f90. We call this “method 4”.
We repeat the same analysis using methods 3 and 4 and we find that the problem
of calculating time accurately practically vanishes. The result of the analysis can
be found on the right plot of figure 2.21. Methods 2 and 4 have no significant
difference in their results, whereas methods 1 and 3 do have a dramatic
difference, with method 3 decreasing the error more than tenfold. The
problem of the increase of systematic errors with decreasing  does not
vanish completely due to the operation x=x+v*dt. This type of error is
harder to deal with and one has to invent more elaborate algorithms in
order to reduce it significantly. This will be discussed further in chapter 4.
does not
vanish completely due to the operation x=x+v*dt. This type of error is
harder to deal with and one has to invent more elaborate algorithms in
order to reduce it significantly. This will be discussed further in chapter 4.
2.3.3 The Two Dimensional Box
A particle is confined to move on the plane in the area  and
and
 . When it reaches the boundaries of this two dimensional box, it
bounces elastically off its walls. The particle is found in an infinite depth
orthogonal potential well. The particle starts moving at time
. When it reaches the boundaries of this two dimensional box, it
bounces elastically off its walls. The particle is found in an infinite depth
orthogonal potential well. The particle starts moving at time  from
from  and our program will calculate its trajectory until time
and our program will calculate its trajectory until time  with time step
with time step  .
Such a trajectory can be seen in figure 2.23.
.
Such a trajectory can be seen in figure 2.23.
If the particle’s position and velocity are known at time  , then at time
, then at time
 they will be given by the relations
they will be given by the relations
The collision of the particle off the walls is modeled by reflection of the
normal component of the velocity when the respective coordinate of the
particle crosses the wall. This is a source of the systematic errors that
we discussed in the previous section. The central loop of the program
is:
i = i + 1
t = t0 + i *dt
x = x + vx*dt
y = y + vy*dt
if(x .lt. 0.0 .or. x .gt. Lx) vx = -vx
if(y .lt. 0.0 .or. y .gt. Ly) vy = -vy
The full program can be found in the file box2D_1.f90. Notice that we
introduced two counters nx and ny of the particle’s collisions with the
walls:
!============================================================
!File box2D_1.f90
!Motion of a free particle in a box 0<x<Lx 0<y<Ly
!Use integration with time step dt: x = x + vx*dt y=y+vy*dt
!------------------------------------------------------------
program box2D
implicit none
!------------------------------------------------------------
!Declaration of variables
real(8) :: Lx,Ly,x0,y0,v0x,v0y,t0,tf,dt,t,x,y,vx,vy
integer :: i,nx,ny
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter Lx,Ly:’
read *,Lx,Ly
print *,’# Lx = ’,Lx,’ Ly= ’,Ly
if( Lx .le. 0.0) stop ’Lx must be positive.’
if( Ly .le. 0.0) stop ’Ly must be positive.’
print *,’# Enter x0,y0,v0x,v0y:’
read *,x0,y0,v0x,v0y
print *,’# x0= ’,x0,’ y0= ’,y0,’ v0x= ’,v0x,’ v0y= ’,v0y
if(x0 .lt. 0.0 .or. x0 .gt. Lx) stop ’illegal value x0’
if(y0 .lt. 0.0 .or. y0 .gt. Ly) stop ’illegal value y0’
if(v0x**2+v0y**2.eq. 0.0 ) stop ’illegal value v0=0’
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
i = 0
nx = 0 ; ny = 0
t = t0
x = x0 ; y = y0
vx = v0x; vy = v0y
open(unit=11,file=’box2D_1.dat’)
!------------------------------------------------------------
!Compute:
do while(t .le. tf)
write(11,*)t,x,y,vx,vy
i = i + 1
t = t0 + i *dt
x = x + vx*dt
y = y + vy*dt
if(x .lt. 0.0 .or. x .gt. Lx) then
vx = -vx
nx = nx + 1
endif
if(y .lt. 0.0 .or. y .gt. Ly) then
vy = -vy
ny = ny + 1
endif
enddo
close(11)
print *,’# Number of collisions:’
print *,’# nx= ’,nx,’ ny= ’,ny
end program box2D
A typical session for the study of a particle’s trajectory could be:
> gfortran box2D_1.f90 -o box
> ./box
# Enter Lx,Ly:
10.0 5.0
# Lx = 10. Ly= 5.
# Enter x0,y0,v0x,v0y:
5.0 0.0 1.27 1.33
# x0= 5. y0= 0. v0x= 1.27 v0y= 1.33
# Enter t0,tf,dt:
0 50 0.01
# t0= 0. tf= 50. dt= 0.01
# Number of collisions:
# nx= 6 ny= 13
> gnuplot
gnuplot> plot "box2D_1.dat" using 1:2 w l title "x (t)"
gnuplot> replot "box2D_1.dat" using 1:3 w l title "y (t)"
gnuplot> plot "box2D_1.dat" using 1:4 w l title "vx(t)"
gnuplot> replot "box2D_1.dat" using 1:5 w l title "vy(t)"
gnuplot> plot "box2D_1.dat" using 2:3 w l title "x-y"
Notice the last line of output from the program: The particle bounces off the
vertical walls 6 times (nx=6) and from the horizontal ones 13 (ny=13). The
gnuplot commands construct the diagrams displayed in figures 2.22 and 2.23.
In order to animate the particle’s trajectory, we can copy the file
box2D_animate.gnu of the accompanying software to the current directory and
give the gnuplot commands:
gnuplot> file = "box2D_1.dat"
gnuplot> Lx = 10 ; Ly = 5
gnuplot> t0 = 0 ; tf = 50; dt = 1
gnuplot> load "box2D_animate.gnu"
gnuplot> t0 = 0 ; dt = 0.5; load "box2D_animate.gnu"
The last line repeats the same animation at half speed. You can also use the file
animate2D.gnu discussed in section 2.1.1. We add new commands in the file
box2D_animate.gnu so that the plot limits are calculated automatically and the
box is drawn on the plot. The arrow drawn is not the position vector with respect
to the origin of the coordinate axes, but the one connecting the initial with the
current position of the particle.
The next step should be to test the accuracy of your results. This can be done
by generalizing the discussion of the previous section and is left as an exercise for
the reader.
2.4 Applications
In this section we will study simple examples of motion in a box with different
types of obstacles. We will start with a game of ... mini golf. The player shoots a
(point) “ball” which moves in an orthogonal box of linear dimensions  and
and
 and which is open on the
and which is open on the  side. In the box there is a circular “hole”
with center at
side. In the box there is a circular “hole”
with center at  and radius
and radius  . If the “ball” falls in the “hole”, the player
wins. If the ball leaves out of the box through its open side, the player
loses. In order to check if the ball is in the hole when it is at position
. If the “ball” falls in the “hole”, the player
wins. If the ball leaves out of the box through its open side, the player
loses. In order to check if the ball is in the hole when it is at position
 , all we have to do is to check whether
, all we have to do is to check whether  .
.
Initially we place the ball at the position  at time
at time  . The
player hits the ball which leaves with initial velocity of magnitude
. The
player hits the ball which leaves with initial velocity of magnitude  at an angle
at an angle
 degrees with the
degrees with the  axis. The program is found in the file MiniGolf.f90 and
is listed below:
axis. The program is found in the file MiniGolf.f90 and
is listed below:
!============================================================
!File MiniGolf.f
!Motion of a free particle in a box 0<x<Lx 0<y<Ly
!The box is open at x=0 and has a hole at (xc,yc) of radius R
!Ball is shot at (0,Ly/2) with speed v0, angle theta (degrees)
!Use integration with time step dt: x = x + vx*dt y=y+vy*dt
!Ball stops in hole (success) or at x=0 (failure)
!------------------------------------------------------------
program MiniGolf
implicit none
!------------------------------------------------------------
!Declaration of variables
real(8) :: Lx,Ly,x0,y0,v0x,v0y,t0,tf,dt,t,x,y,vx,vy
real(8) :: v0,theta,xc,yc,R,R2
real(8), parameter :: PI=3.14159265358979324D0
integer :: i,nx,ny
character(7) :: result
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter Lx,Ly:’
read *,Lx,Ly
print *,’# Lx = ’,Lx,’ Ly= ’,Ly
if( Lx .le. 0.0) stop ’Lx must be positive.’
if( Ly .le. 0.0) stop ’Ly must be positive.’
print *,’# Enter hole position and radius: (xc,yc), R:’
read *,xc,yc,R
print *,’# (xc,yc)= ( ’,xc,’ , ’,yc,’ ) R= ’,R
print *,’# Enter v0, theta(degrees):’
read *,v0,theta
print *,’# v0= ’,v0,’ theta= ’,theta,’ degrees’
if(v0 .le. 0.0D0 ) stop ’illegal value of v0.’
if(ABS(theta).ge. 90.0D0) stop ’illegal value of theta.’
print *,’# Enter dt:’
read *,dt
print *,’# dt= ’,dt
!------------------------------------------------------------
!Initialize
t0 = 0.0D0
x0 = 0.00001D0 ! small but non-zero
y0 = Ly/2.0
R2 = R*R
theta = (PI/180.0D0)*theta
v0x = v0*cos(theta)
v0y = v0*sin(theta)
print *,’# x0= ’,x0,’ y0= ’,y0,’ v0x= ’,v0x,’ v0y= ’,v0y
i = 0
nx = 0 ; ny = 0
t = t0
x = x0 ; y = y0
vx = v0x; vy = v0y
open(unit=11,file=’MiniGolf.dat’)
!------------------------------------------------------------
!Compute:
do while( .TRUE. ) !forever!
write(11,*)t,x,y,vx,vy
i = i + 1
t = t0 + i*dt
x = x + vx*dt
y = y + vy*dt
if(x .gt. Lx) then
vx = -vx
nx = nx + 1
endif
if(y .lt. 0.0 .or. y .gt. Ly) then
vy = -vy
ny = ny + 1
endif
if(x .le. 0.0D0)then
result = ’Failure’
exit !exit do loop
endif
if( ((x-xc)*(x-xc)+(y-yc)*(y-yc)) .le. R2)then
result = ’Success’
exit !exit do loop
endif
enddo
close(11)
print *,’# Number of collisions:’
print *,’# Result= ’,result,’ nx= ’,nx,’ ny= ’,ny
end program MiniGolf
In order to run it, we can use the commands:
> gfortran MiniGolf.f90 -o mg
> ./mg
# Enter Lx,Ly:
10 5
# Lx = 10. Ly= 5.
# Enter hole position and radius: (xc,yc), R:
8 2.5 0.5
# (xc,yc)= ( 8. , 2.5 ) R= 0.5
# Enter v0, theta(degrees):
1 80
# v0= 1. theta= 80. degrees
# Enter dt:
0.01
# dt= 0.01
# x0= 1.E-05 y0= 2.5 v0x= 0.173648178 v0y= 0.984807753
# Number of collisions:
# Result= Success nx= 0 ny= 9
You should construct the plots of the position and the velocity of the particle.
You can also use the animation program found in the file MiniGolf_animate.gnu
for fun. Copy it from the accompanying software to the current directory and give
the gnuplot commands:
gnuplot> file = "MiniGolf.dat"
gnuplot> Lx = 10;Ly = 5
gnuplot> xc = 8; yc = 2.5 ; R = 0.5
gnuplot> t0 = 0; dt = 0.1
gnuplot> load "MiniGolf_animate.gnu"
The results are shown in figure 2.24.
The next example with be three dimensional. We will study the motion of a
particle confined within a cylinder of radius  and height
and height  . The collisions of
the particle with the cylinder are elastic. We take the axis of the cylinder to be
the
. The collisions of
the particle with the cylinder are elastic. We take the axis of the cylinder to be
the  axis and the two bases of the cylinder to be located at
axis and the two bases of the cylinder to be located at  and
and  .
This is shown in figure 2.26.
.
This is shown in figure 2.26.
The collisions of the particle with the bases of the cylinder are easy to
program: we follow the same steps as in the case of the simple box. For the
collision with the cylinder’s side, we consider the projection of the motion on the
 plane. The projection of the particle moves within a circle of radius
plane. The projection of the particle moves within a circle of radius  and center at the intersection of the
and center at the intersection of the  axis with the plane. This is shown in
figure 2.25. At the collision, the
axis with the plane. This is shown in
figure 2.25. At the collision, the  component of the velocity is reflected
component of the velocity is reflected
 , whereas
, whereas  remains the same. The velocity of the particle before the
collision is
remains the same. The velocity of the particle before the
collision is
and after the collision is From the relations and  ,
,  , we have that The inverse relations are With the transformation
, we have that The inverse relations are With the transformation  , the new velocity in Cartesian coordinates
will be
, the new velocity in Cartesian coordinates
will be
The transformation  ,
,  will be performed in the
subroutine reflectVonCircle(vx,vy,x,y,xc,yc,R). Upon entry
to the subroutine, we provide the initial velocity (vx,vy), the collision
point (x,y), the center of the circle (xc,yc) and the radius of the
circle
R. Upon exit from the subroutine, (vx,vy) have been replaced with the new
values
will be performed in the
subroutine reflectVonCircle(vx,vy,x,y,xc,yc,R). Upon entry
to the subroutine, we provide the initial velocity (vx,vy), the collision
point (x,y), the center of the circle (xc,yc) and the radius of the
circle
R. Upon exit from the subroutine, (vx,vy) have been replaced with the new
values
 .
.
The program can be found in the file Cylinder3D.f90 and is listed
below:
!============================================================
!File Cylinder3D.f90
!Motion of a free particle in a cylinder with axis the z-axis,
!radius R and 0<z<L
!Use integration with time step dt: x = x + vx*dt
! y = y + vy*dt
! z = z + vz*dt
!Use subroutine reflectVonCircle for collisions at r=R
!------------------------------------------------------------
program Cylinder3D
implicit none
!------------------------------------------------------------
!Declaration of variables
real(8) :: x0,y0,z0,v0x,v0y,v0z,t0,tf,dt,t,x,y,z,vx,vy,vz
real(8) :: L,R,R2,vxy,rxy,r2xy,xc,yc
integer :: i,nr,nz
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter R, L:’
read *,R,L
print *,’# R= ’,R,’ L= ’,L
if( R .le. 0.0) stop ’R must be positive.’
if( L .le. 0.0) stop ’L must be positive.’
print *,’# Enter x0,y0,z0,v0x,v0y,v0z:’
read *,x0,y0,z0,v0x,v0y,v0z
rxy = DSQRT(x0*x0+y0*y0)
print *,’# x0 = ’,x0 ,’ y0 = ’,y0 ,’ z0= ’,z0, ’ rxy= ’,rxy
print *,’# v0x= ’,v0x,’ v0y= ’,v0y,’ v0z= ’,v0z
if(rxy .gt. R )stop ’illegal value of rxy > R’
if(z0 .lt. 0.0D0 )stop ’illegal value of z0 < 0’
if(z0 .gt. L )stop ’illegal value of z0 > L’
if(v0x**2+v0y**2+v0z**2.eq.0.0)stop ’illegal value of v0 = 0.’
print *,’# Enter t0,tf,dt:’
read *,t0,tf,dt
print *,’# t0= ’,t0,’ tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
i = 0
nr = 0 ; nz = 0
t = t0
x = x0 ; y = y0 ; z = z0
vx = v0x; vy = v0y; vz = v0z
R2 = R*R
xc = 0.0D0 !center of circle which is the projection of the
yc = 0.0D0 !cylinder on the xy plane
open(unit=11,file=’Cylinder3D.dat’)
!------------------------------------------------------------
!Compute:
do while(t .le. tf)
write(11,100)t,x,y,z,vx,vy,vz
i = i + 1
t = t0 + i *dt
x = x + vx*dt
y = y + vy*dt
z = z + vz*dt
if(z .lt. 0.0 .or. z .gt. L) then
vz = -vz ! reflection on cylinder caps
nz = nz + 1
endif
r2xy = x*x+y*y
if( r2xy .gt. R2)then
call reflectVonCircle(vx,vy,x,y,xc,yc,R)
nr = nr + 1
endif
enddo
close(11)
print *,’# Number of collisions:’
print *,’# nr= ’,nr,’ nz= ’,nz
100 FORMAT(100G28.16)
end program Cylinder3D
!------------------------------------------------------------
!============================================================
!------------------------------------------------------------
subroutine reflectVonCircle(vx,vy,x,y,xc,yc,R)
implicit none
real(8) :: vx,vy,x,y,xc,yc,R
real(8) :: theta,cth,sth,vr,vth
theta = atan2(y-yc,x-xc)
cth = cos(theta)
sth = sin(theta)
vr = vx*cth + vy *sth
vth = -vx*sth + vy *cth
vx = -vr*cth - vth*sth !reflect vr -> -vr
vy = -vr*sth + vth*cth
x = xc + R*cth !put x,y on the circle
y = yc + R*sth
end subroutine reflectVonCircle
Notice that the function atan2 is used for computing the angle theta. This
function, when called with two arguments atan2(y,x), returns the angle
 in radians. The correct quadrant of the circle where
in radians. The correct quadrant of the circle where  lies
is chosen. The angle that we want to compute is given by atan2(y-yc,x-xc).
Then we apply equations (2.29) and (2.31) and in the last two lines we enforce
the particle to be at the point
lies
is chosen. The angle that we want to compute is given by atan2(y-yc,x-xc).
Then we apply equations (2.29) and (2.31) and in the last two lines we enforce
the particle to be at the point  , exactly on the circle.
, exactly on the circle.
A typical session is shown below:
> gfortran Cylinder3D.f90 -o cl
> ./cl
# Enter R, L:
10.0 10.0
# R= 10. L= 10.
# Enter x0,y0,z0,v0x,v0y,v0z:
1.0 2.2 3.1 0.93 -0.89 0.74
# x0 = 1. y0 = 2.2 z0= 3.1 rxy= 2.41660919
# v0x= 0.93 v0y= -0.89 v0z= 0.74
# Enter t0,tf,dt:
0.0 500.0 0.01
# t0= 0. tf= 500. dt= 0.01
# Number of collisions:
# nr= 33 nz= 37
In order to plot the position and the velocity as a function of time, we use the
following gnuplot commands:
gnuplot> file="Cylinder3D.dat"
gnuplot> plot file using 1:2 with lines title " x(t)",\
file using 1:3 with lines title " y(t)",\
file using 1:4 with lines title " z(t)"
gnuplot> plot file using 1:5 with lines title "v_x(t)",\
file using 1:6 with lines title "v_y(t)",\
file using 1:7 with lines title "v_z(t)"
We can also compute the distance of the particle from the cylinder’s axis
 as a function of time using the command:
as a function of time using the command:
gnuplot> plot file using 1:(sqrt($2**2+$3**2)) w l t "r(t)"
In order to plot the trajectory, together with the cylinder, we give the
commands:
gnuplot> L = 10 ; R = 10
gnuplot> set urange [0:2.0*pi]
gnuplot> set vrange [0:L]
gnuplot> set parametric
gnuplot> splot file using 2:3:4 with lines notitle,\
R*cos(u),R*sin(u),v notitle
The command set parametric is necessary if one wants to make a parametric plot
of a surface  . The cylinder (without the
bases) is given by the parametric equations
. The cylinder (without the
bases) is given by the parametric equations  with
with  ,
, ![v ∈ [0,L ]](main_latex486x.png) .
.
We can also animate the trajectory with the help of the gnuplot script file
Cylinder3D_animate.gnu. Copy the file from the accompanying software to the
current directory and give the gnuplot commands:
gnuplot> R=10;L=10;t0=0;tf=500;dt=10
gnuplot> load "Cylinder3D_animate.gnu"
The result is shown in figure 2.26.
The last example will be that of a simple model of a spacetime wormhole. This
is a simple spacetime geometry which, in the framework of the theory of general
relativity, describes the connection of two distant areas in space which are
asymptotically flat. This means, that far enough from the wormhole’s mouths,
space is almost flat - free of gravity. Such a geometry is depicted in figure 2.27.
The distance traveled by someone through the mouths could be much smaller
than the distance traveled outside the wormhole and, at least theoretically,
traversable wormholes could be used for interstellar/intergalactic traveling and/or
communications between otherwise distant areas in the universe. Of course we
should note that such macroscopic and stable wormholes are not known to
be possible to exist in the framework of general relativity. One needs
an exotic type of matter with negative energy density which has never
been observed. Such exotic geometries may realize microscopically as
quantum fluctuations of spacetime and make the small scale structure of the
geometry
a “spacetime foam”.
We will study a very simple model of the above geometry on the plane with a particle moving
freely in it .
We take the two dimensional plane and cut two equal disks of radius  with
centers at distance
with
centers at distance  like in figure 2.28. We identify the points on the two circles
such that the point 1 of the left circle is the same as the point 1 on the right
circle, the point 2 on the left with the point 2 on the right etc. The two circles are
given by the parametric equations
like in figure 2.28. We identify the points on the two circles
such that the point 1 of the left circle is the same as the point 1 on the right
circle, the point 2 on the left with the point 2 on the right etc. The two circles are
given by the parametric equations  ,
,  ,
,
 for the right circle and
for the right circle and  ,
,  ,
,
 for the left. Points on the two circles with the same
for the left. Points on the two circles with the same  are
identified. A particle entering the wormhole from the left circle with velocity
are
identified. A particle entering the wormhole from the left circle with velocity  is
immediately exiting from the right with velocity
is
immediately exiting from the right with velocity  as shown in figure
2.28.
as shown in figure
2.28.
Then we will do the following:
- Write a program that computes the trajectory of a particle moving
in the geometry of figure 2.28. We set the limits of motion to be
 and
and  . We will use periodic
boundary conditions in order to define what happens when the
particle attempts to move outside these limits. This means that we
identify the
. We will use periodic
boundary conditions in order to define what happens when the
particle attempts to move outside these limits. This means that we
identify the  line with the
line with the  line as well as
the
line as well as
the  line with the
line with the  line. The user enters the
parameters
line. The user enters the
parameters  ,
,  and
and  as well as the initial conditions
as well as the initial conditions  ,
,
 where
where  . The user will also provide
the time parameters
. The user will also provide
the time parameters  and
and  for motion in the time interval
for motion in the time interval
![t ∈ [t = 0,t ]
0 f](main_latex518x.png) with step
with step  .
.
- Plot the particle’s trajectory
with
 ,
, 
 ,
,  in
the geometry with
in
the geometry with  .
.
- Find a closed trajectory which does not cross the boundaries
 ,
,  and determine whether it is stable under small
perturbations of the initial conditions.
and determine whether it is stable under small
perturbations of the initial conditions.
- Find other closed trajectories that go through the mouths of the
wormhole and study their stability under small perturbations of the
initial conditions.
- Add to the program the option to calculate the distance traveled
by the particle. If the particle starts from
 and moves in
the
and moves in
the  direction to the
direction to the  ,
,  position, draw the
trajectory and calculate the distance traveled on paper. Then confirm
your calculation from the numerical result coming from your program.
position, draw the
trajectory and calculate the distance traveled on paper. Then confirm
your calculation from the numerical result coming from your program.
- Change the boundary conditions, so that the particle bounces off
elastically at
 ,
,  and replot all the trajectories
mentioned above.
and replot all the trajectories
mentioned above.
Define the right circle  by the parametric equations
by the parametric equations
 | (2.32) |
and the left circle  by the parametric equations
by the parametric equations
 | (2.33) |
The particle’s position changes at time  by
by
for  for given
for given  ,
,  and as long as
and as long as  . If the point
. If the point
 is outside the boundaries
is outside the boundaries  ,
,  , we redefine
, we redefine
 ,
,  in each case respectively. Points defined by the same
value of
in each case respectively. Points defined by the same
value of  are identified, i.e. they represent the same points of space. If the point
are identified, i.e. they represent the same points of space. If the point
 crosses either one of the circles
crosses either one of the circles  or
or  , then we take the particle out
from the other circle.
, then we take the particle out
from the other circle.
Crossing the circle  is determined by the relation
is determined by the relation
 | (2.35) |
The angle  is calculated from the equation
is calculated from the equation
 | (2.36) |
and the point  is mapped to the point
is mapped to the point  where
where
 | (2.37) |
as can be seen in figure 2.29. For mapping  , we first calculate the
vectors
, we first calculate the
vectors
 | (2.38) |
so that the velocity
 | (2.39) |
where the radial components are  and
and  . Therefore, the
relations that give the “emerging” velocity
. Therefore, the
relations that give the “emerging” velocity  are:
are:
 | (2.40) |
Similarly we calculate the case of entering from  and emerging from
and emerging from  .
The condition now is:
.
The condition now is:
 | (2.41) |
The angle  is given by
is given by
 | (2.42) |
and the point  is mapped to the point
is mapped to the point  where
where
 | (2.43) |
For mapping  , we calculate the vectors
, we calculate the vectors
 | (2.44) |
so that the velocity
 | (2.45) |
The emerging velocity  is:
is:
 | (2.46) |
Systematic errors are now coming from crossing the two mouths of the
wormhole. There are no systematic errors from crossing the boundaries
 ,
,  (why?). Try to think of ways to control those errors and
study them.
(why?). Try to think of ways to control those errors and
study them.
The closed trajectories that we are looking for come from the initial
conditions
 | (2.47) |
and they connect points 1 of figure 2.28. They are unstable, as can be seen by
taking  .
.
The closed trajectories that cross the wormhole and “wind” through space can
come from the initial conditions

and cross the points  and
and  respectively. They are also
unstable, as can be easily verified by using the program that you will write. The
full program is listed below:
respectively. They are also
unstable, as can be easily verified by using the program that you will write. The
full program is listed below:
!============================================================
program WormHole2D
implicit none
!------------------------------------------------------------
!Declaration of variables
real(8), parameter :: PI=3.14159265358979324D0
real(8) :: Lx,Ly,L,R,d
real(8) :: x0,y0,v0,theta
real(8) :: t0,tf,dt
real(8) :: t,x,y,vx,vy
real(8) :: xc1,yc1,xc2,yc2,r1,r2
integer :: i
!------------------------------------------------------------
!Ask user for input:
print *,’# Enter L,d,R:’
read *,L,d,R
print *,’# L= ’,L,’ d= ’,d,’ R= ’,R
if( L .le. d+2.0D0*R) stop ’L <= d+2*R’
if( d .le. 2.0D0*R) stop ’d <= 2*R’
print *,’# Enter (x0,y0), v0, theta(degrees):’
read *,x0,y0,v0,theta
print *,’# x0= ’,x0,’ y0 = ’,y0
print *,’# v0= ’,v0,’ theta= ’,theta,’ degrees’
if(v0 .le. 0.0D0 ) stop ’illegal value of v0.’
print *,’# Enter tf, dt:’
read *,tf,dt
print *,’# tf= ’,tf,’ dt= ’,dt
!------------------------------------------------------------
!Initialize
theta = (PI/180.0D0)*theta
i = 0
t = 0.0D0
x = x0 ; y = y0
vx = v0*cos(theta); vy = v0*sin(theta)
print *,’# x0= ’,x,’ y0= ’,y,’ v0x= ’,vx,’ v0y= ’,vy
!Wormhole’s centers:
xc1 = 0.5D0*d; yc1 = 0.0D0
xc2 = -0.5D0*d; yc2 = 0.0D0
!Box limits coordinates:
Lx = 0.5D0*L; Ly = 0.5D0*L
!Test if already inside cut region:
r1 = sqrt((x-xc1)**2+(y-yc1)**2)
r2 = sqrt((x-xc2)**2+(y-yc2)**2)
if( r1 .le. R ) stop ’r1 <= R’
if( r2 .le. R ) stop ’r2 <= R’
!Test if outside box limits:
if(ABS(x) .ge. Lx) stop ’|x| >= Lx’
if(ABS(y) .ge. Ly) stop ’|y| >= Ly’
open(unit=11,file=’Wormhole.dat’)
!------------------------------------------------------------
!Compute:
do while( t .lt. tf )
write(11,*)t,x,y,vx,vy
i = i+1
t = i*dt
x = x + vx*dt; y = y + vy*dt
! Toroidal boundary conditions:
if( x .gt. Lx) x = x - L
if( x .lt. -Lx) x = x + L
if( y .gt. Ly) y = y - L
if( y .lt. -Ly) y = y + L
! Test if inside the cut disks
r1 = sqrt((x-xc1)**2+(y-yc1)**2)
r2 = sqrt((x-xc2)**2+(y-yc2)**2)
if( r1 .lt. R)then
! Notice: we pass r1 as radius of circle, not R
call crossC1(x,y,vx,vy,dt,r1,d)
else if( r2 .lt. R)then
call crossC2(x,y,vx,vy,dt,r2,d)
endif
! small chance here that still in C1 or C2, but OK since
! another dt-advance given at the beginning of do-loop
enddo !do while( t .lt. tf )
end program WormHole2D
!=======================================================
subroutine crossC1(x,y,vx,vy,dt,R,d)
implicit none
real(8) :: x,y,vx,vy,dt,R,d
real(8) :: vr,v0 !v0 -> vtheta
real(8) :: theta,xc,yc
print *,’# Inside C1: (x,y,vx,vy,R)= ’,x,y,vx,vy,R
xc = 0.5D0*d !center of C1
yc = 0.0D0
theta = atan2(y-yc,x-xc)
x = -xc - R*cos(theta) !new x-value, y invariant
!Velocity transformation:
vr = vx*cos(theta)+vy*sin(theta)
v0 = -vx*sin(theta)+vy*cos(theta)
vx = vr*cos(theta)+v0*sin(theta)
vy = -vr*sin(theta)+v0*cos(theta)
!advance x,y, hopefully outside C2:
x = x + vx*dt
y = y + vy*dt
print *,’# Exit C2: (x,y,vx,vy )= ’,x,y,vx,vy
end subroutine crossC1
!=======================================================
subroutine crossC2(x,y,vx,vy,dt,R,d)
implicit none
real(8), parameter :: PI=3.14159265358979324D0
real(8) :: x,y,vx,vy,dt,R,d
real(8) :: vr,v0 !v0 -> vtheta
real(8) :: theta,xc,yc
print *,’# Inside C2: (x,y,vx,vy,R)= ’,x,y,vx,vy,R
xc = -0.5D0*d !center of C2
yc = 0.0D0
theta = PI-atan2(y-yc,x-xc)
x = -xc + R*cos(theta) !new x-value, y invariant
!Velocity transformation:
vr = -vx*cos(theta)+vy*sin(theta)
v0 = vx*sin(theta)+vy*cos(theta)
vx = -vr*cos(theta)-v0*sin(theta)
vy = -vr*sin(theta)+v0*cos(theta)
!advance x,y, hopefully outside C1:
x = x + vx*dt
y = y + vy*dt
print *,’# Exit C1: (x,y,vx,vy )= ’,x,y,vx,vy
end subroutine crossC2
It is easy to compile and run the program. See also the files Wormhole.csh and
Wormhole_animate.gnu of the accompanying software and run the gnuplot
commands:
gnuplot> file = "Wormhole.dat"
gnuplot> R=1;d=5;L=20;
gnuplot> ! ./Wormhole.csh
gnuplot> t0=0;dt=0.2;load "Wormhole_animate.gnu"
You are now ready to answer the rest of the questions that we asked in our
list.
2.5 Problems
- Change the program Circle.f90 so that it prints the number of full
circles traversed by the particle.
- Add all the necessary tests on the parameters entered by the user in
the program Circle.f90, so that the program is certain to run without
problems. Do the same for the rest of the programs given in the same
section.
- A particle moves with constant angular velocity
 on a circle that
has the origin of the coordinate system at its center. At time
on a circle that
has the origin of the coordinate system at its center. At time  ,
the particle is at
,
the particle is at 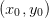 . Write the program CircularMotion.f90
that will calculate the particle’s trajectory. The user should enter the
parameters
. Write the program CircularMotion.f90
that will calculate the particle’s trajectory. The user should enter the
parameters  . The program should print the results
like the program Circle.f90 does.
. The program should print the results
like the program Circle.f90 does.
- Change the program SimplePendulum.f90 so that the user could enter
a non zero initial velocity.
- Study the
 limit in the projectile motion given by equations
(2.10) . Expand
limit in the projectile motion given by equations
(2.10) . Expand  and keep the non
vanishing terms as
and keep the non
vanishing terms as  . Then keep the next order leading terms
which have a smaller power of
. Then keep the next order leading terms
which have a smaller power of  . Program these relations in a file
. Program these relations in a file
ProjectileSmallAirResistance.f90. Consider the initial conditions
 and calculate the range of the trajectory numerically by
using the two programs
and calculate the range of the trajectory numerically by
using the two programs
ProjectileSmallAirResistance.f90,
ProjectileAirResistance.f90. Determine the range of values of  for which the two results agree within 5% accuracy.
for which the two results agree within 5% accuracy.
- Write a program for a projectile which moves through a fluid with
fluid resistance proportional to the square of the velocity. Compare
the range of the trajectory with the one calculated by the program
ProjectileAirResistance.f90 for the parameters shown in figure
2.10.
- Change the program Lissajous.f90 so that the user can enter a
different amplitude and initial phase in each direction. Study the case
where the amplitudes are the same and the phase difference in the two
directions are
 . Repeat by taking the amplitude in the
. Repeat by taking the amplitude in the
 direction to be twice as much the amplitude in the
direction to be twice as much the amplitude in the  direction.
direction.
- Change the program ProjectileAirResistance.f90, so that it can
calculate also the
 case.
case.
- Change the program ProjectileAirResistance.f90 so that it can
calculate the trajectory of the particle in three dimensional space. Plot
the position coordinates and the velocity components as a function of
time. Plot the three dimensional trajectory using splot in gnuplot
and animate the trajectory using the gnuplot script animate3D.gnu.
- Change the program ChargeInB.f90 so that it can calculate the
number of full revolutions that the projected particle’s position on the
 plane makes during its motion.
plane makes during its motion.
- Change the program box1D_1.f90 so that it prints the number of
the particle’s collisions on the left wall, on the right wall and the total
number of collisions to the stdout.
- Do the same for the program box1D_2.f90. Fill the table on page 311
the number of calculated collisions and comment on the results.
- Run the program box1D_1.f90 and choose L= 10, v0=1. Decrease the
step dt up to the point that the particle stops to move. For which value
of dt this happens? Increase v0=10,100. Until which value of dt the
particle moves now? Why?
- Change the REAL declarations to REAL(8) in the program
box1D_1.f90. Add explicit exponents D0 to all constants (e.g.
0.0
 0.0D0). Compare your results to those obtained in section
2.3.2. Repeat problem 2.13. What do you observe?
0.0D0). Compare your results to those obtained in section
2.3.2. Repeat problem 2.13. What do you observe?
- Change the program box1D_1.f90 so that you can study non elastic
collisions
 ,
,  with the walls.
with the walls.
- Change the program box2D_1.f90 so that you can study inelastic
collisions with the walls, such that
 ,
,  ,
,
 .
.
- Use the method of calculating time in the programs box1D_4.f90 and
box1D_5.f90 in order to produce the results in figure 2.21.
- Particle falls freely moving in the vertical direction. It starts with
zero velocity at height
 . Upon reaching the ground, it bounces
inelastically such that
. Upon reaching the ground, it bounces
inelastically such that  with
with  a parameter. Write
the necessary program in order to study numerically the particle’s
motion and study the cases
a parameter. Write
the necessary program in order to study numerically the particle’s
motion and study the cases  .
.
- Generalize the program of the previous problem so that you can study
the case
 . Animate the calculated trajectories.
. Animate the calculated trajectories.
- Study the motion of a particle moving inside the box of figure 2.30. Count
the number of collisions of the particle with the walls before it leaves the
box.
- Study the motion of the point particle on the “billiard table” of figure 2.31.
Count the number of collisions with the walls before the particle enters into
a hole. The program should print from which hole the particle left the table.
- Write a program in order to study the motion of a particle in the box of
figure 2.32. At the center of the box there is a disk on which the particle
bounces off elastically (Hint: use the routine reflectVonCircle of the
program Cylinder3D.f90).
- In the box of the previous problem, put four disks on which the particle
bounces of elastically like in figure 2.33.
- Consider the arrangement of figure 2.34. Each time the particle bounces
elastically off a circle, the circle disappears. The game is over successfully if
all the circles vanish. Each time the particle bounces off on the wall to the
left, you lose a point. Try to find trajectories that minimize the number of
lost points.
Chapter 3
Logistic Map
Nonlinear differential equations model interesting dynamical systems in physics,
biology and other branches of science. In this chapter we perform a numerical
study of the discrete logistic map as a “simple mathematical model with complex
dynamical properties” [21] similar to the ones encountered in more complicated
and interesting dynamical systems. For certain values of the parameter of the
map, one finds chaotic behavior giving us an opportunity to touch on this very
interesting topic with important consequences in physical phenomena. Chaotic
evolution restricts out ability for useful predictions in an otherwise fully
deterministic dynamical system: measurements using slightly different initial
conditions result in a distribution which is indistinguishable from the distribution
coming from sampling a random process. This scientific field is huge and active
and we refer the reader to the bibliography for a more complete introduction
[21, 22, 23, 24, 25, 26, 27, 38].
3.1 Introduction
The most celebrated application of the logistic map comes from the study of
population growth in biology. One considers populations which reproduce at fixed
time intervals and whose generations do not overlap.
The simplest (and most naive) model is the one that makes the reasonable
assumption that the rate of population growth  of a population
of a population  is
proportional to the current population:
is
proportional to the current population:
 | (3.1) |
The general solution of the above equation is  showing an
exponential population growth for
showing an
exponential population growth for  an decline for
an decline for  . It is obvious that
this model is reasonable as long as the population is small enough so that the
interaction with its environment (adequate food, diseases, predators etc)
can be neglected. The simplest model that takes into account some of
the factors of the interaction with the environment (e.g. starvation) is
obtained by the introduction of a simple non linear term in the equation so
that
. It is obvious that
this model is reasonable as long as the population is small enough so that the
interaction with its environment (adequate food, diseases, predators etc)
can be neglected. The simplest model that takes into account some of
the factors of the interaction with the environment (e.g. starvation) is
obtained by the introduction of a simple non linear term in the equation so
that
 | (3.2) |
The parameter  gives the maximum growth rate of the population and
gives the maximum growth rate of the population and  controls the ability of the species to maintain a certain population level. The
equation (3.2) can be discretized in time by assuming that each generation
reproduces every
controls the ability of the species to maintain a certain population level. The
equation (3.2) can be discretized in time by assuming that each generation
reproduces every  and that the n-th generation has population
and that the n-th generation has population  where
where  . Then
. Then  and equation (3.1)
becomes
and equation (3.1)
becomes
 | (3.3) |
where  . The solutions of the above equation are well approximated
by
. The solutions of the above equation are well approximated
by 
 so that we have population growth when
so that we have population growth when
 and decline when
and decline when  . Equation (3.2) can be discretized as
follows:
. Equation (3.2) can be discretized as
follows:
 | (3.4) |
Defining  we obtain the logistic map
we obtain the logistic map
 | (3.5) |
We define the functions
 | (3.6) |
(their only difference is that, in the first one,  is considered as a given
parameter), so that
is considered as a given
parameter), so that
 | (3.7) |
where we use the notation  ,
,  ,
,  ,
,
 for function composition. In what follows, the derivative of
for function composition. In what follows, the derivative of  will be
useful:
will be
useful:
 | (3.8) |
Since we interpret  to be the fraction of the population with
respect to its maximum value, we should have
to be the fraction of the population with
respect to its maximum value, we should have  for
each
for
each
 . The function
. The function  has one global maximum for
has one global maximum for  which is equal
to
which is equal
to  . Therefore, if
. Therefore, if  , then
, then  , which for an
appropriate choice of
, which for an
appropriate choice of  will lead to
will lead to  for some value of
for some value of  .
Therefore, the interval of values of
.
Therefore, the interval of values of  which is of interest for our model
is
which is of interest for our model
is
 | (3.9) |
The logistic map (3.5) may be viewed as a finite difference equation and it
is a one step inductive relation. Given an initial value  , a sequence
of values
, a sequence
of values 




 is produced. This will be
referred
to as the trajectory of
is produced. This will be
referred
to as the trajectory of  . In the following sections we will study the properties of
these trajectories as a function of the parameter
. In the following sections we will study the properties of
these trajectories as a function of the parameter  .
.
The solutions of the logistic map are not known except in special cases. For
 we have
we have
 | (3.10) |
and for

 | (3.11) |
For  ,
,  whereas for
whereas for  we have periodic trajectories
resulting in rational
we have periodic trajectories
resulting in rational  and non periodic resulting in irrational
and non periodic resulting in irrational  . For other
values of
. For other
values of  we have to resort to a numerical computation of the trajectories of
the logistic map.
we have to resort to a numerical computation of the trajectories of
the logistic map.
3.2 Fixed Points and  Cycles
Cycles
It is obvious that if the point  is a solution of the equation
is a solution of the equation  , then
, then


 for every
for every  . For the function
. For the function  we have two solutions
we have two solutions
 | (3.12) |
We will see that for appropriate values of  , these solutions are attractors of
most of the trajectories. This means that for a range of values for the initial point
, these solutions are attractors of
most of the trajectories. This means that for a range of values for the initial point
 , the sequence
, the sequence  approaches asymptotically one of these points as
approaches asymptotically one of these points as
 . Obviously the (measure zero) sets of initial values
. Obviously the (measure zero) sets of initial values  and
and
 result in trajectories attracted by
result in trajectories attracted by  and
and  respectively. In
order to determine which one of the two values is preferred, we need to study the
stability of the fixed points
respectively. In
order to determine which one of the two values is preferred, we need to study the
stability of the fixed points  and
and  . For this, assume that for some
value of
. For this, assume that for some
value of  ,
,  is infinitesimally close to the fixed point
is infinitesimally close to the fixed point 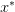 so that
so that
Since
 | (3.14) |
where we used the Taylor expansion of the analytic function  about
about
 and the relation
and the relation  , we have that
, we have that  . Then we
obtain
. Then we
obtain
 | (3.15) |
Therefore, if  we obtain
we obtain  and the fixed point
and the fixed point  is
stable: the sequence
is
stable: the sequence  approaches
approaches  asymptotically. If
asymptotically. If  then the sequence
then the sequence  deviates away from
deviates away from  and the fixed point is
unstable. The limiting case
and the fixed point is
unstable. The limiting case  should be studied separately
and it indicates a change in the stability properties of the fixed point. In
the following discussion, these points will be shown to be bifurcation
points.
should be studied separately
and it indicates a change in the stability properties of the fixed point. In
the following discussion, these points will be shown to be bifurcation
points.
For the function  with
with  we have that
we have that
 and
and  . Therefore, if
. Therefore, if  the point
the point  is an
attractor, whereas the point
is an
attractor, whereas the point  is irrelevant. When
is irrelevant. When  ,
the point
,
the point  results in
results in  , therefore
, therefore  is unstable.
Any initial value
is unstable.
Any initial value  near
near  deviates from it. Since for
deviates from it. Since for  we
have that
we
have that  , the point
, the point  is an attractor. Any
initial value
is an attractor. Any
initial value  approaches
approaches  . When
. When  we
have the limiting case
we
have the limiting case  and we say that at the critical value
and we say that at the critical value
 the fixed point
the fixed point  bifurcates to the two fixed points
bifurcates to the two fixed points  and
and
 .
.
As  increases, the fixed points continue to bifurcate. Indeed, when
increases, the fixed points continue to bifurcate. Indeed, when
 we have that
we have that  and for
and for  the point
the point  becomes unstable. Consider the solution of the equation
becomes unstable. Consider the solution of the equation  . If
. If
 is one of its solutions and for some
is one of its solutions and for some  we have that
we have that  , then
, then





 and
and 
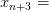



 (therefore
(therefore  is also a solution). If
is also a solution). If 
 are two such different solutions with
are two such different solutions with  ,
,  , then the
trajectory is periodic with period 2. The points
, then the
trajectory is periodic with period 2. The points  ,
,  are such that they are
real solutions of the equation
are such that they are
real solutions of the equation
 | (3.16) |
and at the same time they are not the solutions 
 of the
equation
of the
equation
 , the polynomial above can be written in the form (see [22] for more
details)
, the polynomial above can be written in the form (see [22] for more
details)
 | (3.17) |
By expanding the polynomials (3.16) , (3.17) and comparing their coefficients
we conclude that  ,
,  and
and  . The
roots of the trinomial in (3.17) are determined by the discriminant
. The
roots of the trinomial in (3.17) are determined by the discriminant
 . For the values of
. For the values of  of interest (
of interest ( ), the
discriminant becomes positive when
), the
discriminant becomes positive when  and we have two different
solutions
and we have two different
solutions
 | (3.18) |
When  we have one double root, therefore a unique fixed point.
we have one double root, therefore a unique fixed point.
The study of the stability of the solutions of  requires
the same steps that led to the equation (3.15) and we determine if the
absolute value of
requires
the same steps that led to the equation (3.15) and we determine if the
absolute value of  is greater, less or equal to one. By noting
that
is greater, less or equal to one. By noting
that



 , we see that for
, we see that for
 ,
, 
 and for
and for  ,
,

 . For the intermediate values
. For the intermediate values  the
derivatives
the
derivatives  for
for  . Therefore, these points are stable
solutions of
. Therefore, these points are stable
solutions of  and the points
and the points  bifurcate to
bifurcate to  ,
,  for
for  . Almost all trajectories with initial points in the interval
. Almost all trajectories with initial points in the interval
![[0,1]](main_latex830x.png) are attracted by the periodic trajectory with period 2, the “2-cycle”
are attracted by the periodic trajectory with period 2, the “2-cycle”
 .
.
Using similar arguments we find that the fixed points  ,
,  bifurcate to the eight fixed points
bifurcate to the eight fixed points  ,
,  when
when  .
These are real solutions of the equation that gives the 4-cycle
.
These are real solutions of the equation that gives the 4-cycle  .
For
.
For  , the points
, the points  ,
,  are a stable
4-cycle which is an attractor of almost all trajectories of the logistic
map .
Similarly, for
are a stable
4-cycle which is an attractor of almost all trajectories of the logistic
map .
Similarly, for  the 16 fixed points of the equation
the 16 fixed points of the equation
 give a stable 8-cycle, for
give a stable 8-cycle, for  a stable 16-cycle
etc .
This is the phenomenon which is called period doubling which continues ad
infinitum. The points
a stable 16-cycle
etc .
This is the phenomenon which is called period doubling which continues ad
infinitum. The points  are getting closer to each other as
are getting closer to each other as  increases so that
increases so that
 . As we will see,
. As we will see,  marks the onset
of the non-periodic, chaotic behavior of the trajectories of the logistic
map.
marks the onset
of the non-periodic, chaotic behavior of the trajectories of the logistic
map.
Computing the bifurcation points becomes quickly intractable and we have to
resort to a numerical computation of their values. Initially we will write a program
that computes trajectories of the logistic map for chosen values of  and
and
 . The program can be found in the file logistic.f90 and is listed
below:
. The program can be found in the file logistic.f90 and is listed
below:
!===========================================================
!Discrete Logistic Map
!===========================================================
program logistic_map
implicit none
integer :: NSTEPS,i
real(8) :: r,x0,x1
! ----- Input:
print *,’# Enter NSTEPS, r, x0:’
read *,NSTEPS,r,x0
print *,’# NSTEPS = ’,NSTEPS
print *,’# r = ’,r
print *,’# x0 = ’,x0
! ----- Initialize:
open(unit=33,file=’log.dat’)
write(33,*) 0,x0
! ----- Calculate:
do i=1,NSTEPS
x1 = r * x0 * (1.0D0-x0)
write(33,*)i,x1
x0 = x1
enddo
close(33)
end program logistic_map
The program is compiled and run using the commands:
> gfortran logistic.f90 -o l
> echo "100 0.5 0.1" | ./l
The command echo prints to the stdout the values of the parameters
NSTEPS=100, r=0.5 and x0=0.1. Its stdout is redirected to the stdin of the
command ./l by using a pipe via the symbol |, from which the program reads
their value and uses them in the calculation. The results can be found
in two columns in the file log.dat and can be plotted using gnuplot.
The plots are put in figure 3.1 and we can see the first two bifurcations
when  goes past the values
goes past the values  and
and  . Similarly, we can study
trajectories which are
. Similarly, we can study
trajectories which are  -cycles when
-cycles when  crosses the values
crosses the values  .
.
Another way to depict the 2-cycles is by constructing the cobweb plots: We
start from the point  and we calculate the point
and we calculate the point  , where
, where
 . This point belongs on the curve
. This point belongs on the curve  . The point
. The point  is
then projected on the diagonal
is
then projected on the diagonal  and we obtain the point
and we obtain the point  . We
repeat
. We
repeat  times obtaining the points
times obtaining the points  and
and  on
on  and
and  respectively. The fixed points
respectively. The fixed points  are at the intersections of
these curves and, if they are attractors, the trajectories will converge on them. If
we have a
are at the intersections of
these curves and, if they are attractors, the trajectories will converge on them. If
we have a  -cycle, we will observe a periodic trajectory going through
points which are solutions to the equation
-cycle, we will observe a periodic trajectory going through
points which are solutions to the equation  . This exercise can
be done by using the following program, which can be found in the file
logistic1.f90:
. This exercise can
be done by using the following program, which can be found in the file
logistic1.f90:
!===========================================================
! Discrete Logistic Map
! Map the trajectory in 2d space (plane)
!===========================================================
program logistic_map
implicit none
integer :: NSTEPS,i
real(8) :: r,x0,x1
! ----- Input:
print *,’# Enter NSTEPS, r, x0:’
read *,NSTEPS,r,x0
print *,’# NSTEPS = ’,NSTEPS
print *,’# r = ’,r
print *,’# x0 = ’,x0
! ----- Initialize:
open(unit=33,file=’trj.dat’)
! ----- Calculate:
write(33,*) 0, x0,0
do i=1,NSTEPS
x1 = r * x0 * (1.0D0-x0)
write(33,*) 2*i-3,x0,x1
write(33,*) 2*i-2,x1,x1
x0 = x1
enddo
close(33)
end program logistic_map
Compiling and running this program is done exactly as in the case of the
program in logistic.f90. We can plot the results using gnuplot. The plot in
figure 3.2 can be constructed using the commands:
gnuplot> set size square
gnuplot> f(x) = r*x*(1.0-x)
gnuplot> r = 3.3
gnuplot> plot "<echo 50 3.3 0.2|./l;cat trj.dat" using 2:3 w l
gnuplot> replot f(x) ,f(f(x)),x
The plot command shown above, runs the program exactly as it is done on the
command line. This is accomplished by using the symbol <, which reads the plot
from the stdout of the command "echo 50 3.3 0.2|./l;cat trj.dat". Only
the second command "echo trj.dat" writes to the stdout, therefore the plot is
constructed from the contents of the file trj.dat. The following line adds
the plots of the functions  ,
,  and of the diagonal
and of the diagonal
 . Figures 3.2 and 3.3 show examples of attractors which are fixed
points, 2-cycles and 4-cycles. An example of a non periodic trajectory
is also shown, which exhibits chaotic behavior which can happen when
. Figures 3.2 and 3.3 show examples of attractors which are fixed
points, 2-cycles and 4-cycles. An example of a non periodic trajectory
is also shown, which exhibits chaotic behavior which can happen when
 .
.
3.3 Bifurcation Diagrams
The bifurcations of the fixed points of the logistic map discussed in the previous
section can be conveniently shown on the “bifurcation diagram”. We remind
to the reader that the first bifurcations happen at the critical values of
r
 | (3.19) |
where  ,
,  ,
,  and
and 
 .
For
.
For  we have
we have  fixed points
fixed points  ,
,  of
of
 . By plotting these points
. By plotting these points  as a function of
as a function of  we construct
the bifurcation diagram. These can be calculated numerically by using the
program bifurcate.f90. In this program, the user selects the values of
we construct
the bifurcation diagram. These can be calculated numerically by using the
program bifurcate.f90. In this program, the user selects the values of  that
she needs to study and for each one of them the program records the point of the
that
she needs to study and for each one of them the program records the point of the
 -cycles
-cycles
 ,
,  . This is easily done by computing the
logistic map several times until we are sure that the trajectories reach the stable
state. The parameter NTRANS in the program determines the number of points
that we throw away, which should contain all the transient behavior. After
NTRANS steps, the program records NSTEPS points, where NSTEPS should be
large enough to cover all the points of the
. This is easily done by computing the
logistic map several times until we are sure that the trajectories reach the stable
state. The parameter NTRANS in the program determines the number of points
that we throw away, which should contain all the transient behavior. After
NTRANS steps, the program records NSTEPS points, where NSTEPS should be
large enough to cover all the points of the  -cycles or depict a dense
enough set of values of the non periodic orbits. The program is listed
below:
-cycles or depict a dense
enough set of values of the non periodic orbits. The program is listed
below:
!===========================================================
! Bifurcation Diagram of the Logistic Map
!===========================================================
program bifurcation_diagram
implicit none
real(8),parameter :: rmin = 2.5D0
real(8),parameter :: rmax = 4.0D0
integer,parameter :: NTRANS = 500 !Number of discarded steps
integer,parameter :: NSTEPS = 100 !Number of recorded steps
integer,parameter :: RSTEPS = 2000 !Number of values of r
integer :: i
real(8) :: r,dr,x0,x1
! ----- Initialize:
open(unit=33,file=’bif.dat’)
dr = (rmax-rmin)/RSTEPS !Increment in r
! ----- Calculate:
r = rmin
do while ( r .le. rmax)
x0 = 0.5D0
! ---- Transient steps: skip
do i=1,NTRANS
x1 = r * x0 * (1.0D0-x0)
x0 = x1
enddo
do i=1,NSTEPS
x1 = r * x0 * (1.0D0-x0)
write(33,*) r,x1
x0 = x1
enddo
r = r + dr
enddo ! do while
close(33)
end program bifurcation_diagram
The program can be compiled and run using the commands:
> gfortran bifurcate.f90 -o b
> ./b;
The left plot of figure 3.4 can be constructed by the gnuplot commands:
gnuplot> plot "bif.dat" with dots
We observe the fixed points and the  -cycles for
-cycles for  . When
. When  goes
past
goes
past  , the trajectories become non-periodic and exhibit chaotic behavior.
Chaotic behavior will be discussed more extensively in the next section. For the
time being, we note that if we measure the distance between the points
, the trajectories become non-periodic and exhibit chaotic behavior.
Chaotic behavior will be discussed more extensively in the next section. For the
time being, we note that if we measure the distance between the points
 , we find that it decreases constantly with
, we find that it decreases constantly with  so
that
so
that
 | (3.20) |
where  is the Feigenbaum constant. An additional constant
is the Feigenbaum constant. An additional constant  , defined by the
quotient of the separation of adjacent elements
, defined by the
quotient of the separation of adjacent elements  of period doubled attractors
from one double to the next
of period doubled attractors
from one double to the next  , is
, is
 | (3.21) |
It is also interesting to note the appearance of a 3-cycle right after
 ! By using the theorem of Sharkovskii, Li and
Yorke
showed that any one dimensional system has 3-cycles, therefore it will have cycles
of any length and chaotic trajectories. The stability of the 3-cycle can be studied
from the solutions of
! By using the theorem of Sharkovskii, Li and
Yorke
showed that any one dimensional system has 3-cycles, therefore it will have cycles
of any length and chaotic trajectories. The stability of the 3-cycle can be studied
from the solutions of  in exactly the same way that we did in
equations (3.16) and (3.17) (see [22] for details). Figure 3.5 magnifies a branch
of the 3-cycle. By magnifying different regions in the bifurcation plot, as shown in
the right plot of figure 3.4, we find similar shapes to the branching of the 3-cycle.
in exactly the same way that we did in
equations (3.16) and (3.17) (see [22] for details). Figure 3.5 magnifies a branch
of the 3-cycle. By magnifying different regions in the bifurcation plot, as shown in
the right plot of figure 3.4, we find similar shapes to the branching of the 3-cycle.
Figure 3.4 shows that between intervals of chaotic behavior we obtain
“windows” of periodic trajectories. These are infinite but countable. It is also
quite interesting to note that if we magnify a branch withing these windows, we
obtain a diagram that is similar to the whole diagram! We say that the
bifurcation diagram exhibits self similarity. There are more interesting properties
of the bifurcation diagram and we refer the reader to the bibliography for a more
complete exposition.
We close this section by mentioning that the qualitative properties
of the bifurcation diagram are the same for a whole class of functions.
Feigenbaum discovered that if one takes any function that is concave
and has a unique global maximum, its bifurcation diagram behaves
qualitatively the same way as that of the logistic map. Examples of such
functions
studied in the literature are  ,
,  and
and  .
The constants
.
The constants  and
and  of equations (3.20) and (3.21) are the same
of all these mappings. The functions that result in chaotic behavior are
studied extensively in the literature and you can find a list of those in
[28].
of equations (3.20) and (3.21) are the same
of all these mappings. The functions that result in chaotic behavior are
studied extensively in the literature and you can find a list of those in
[28].
3.4 The Newton-Raphson Method
In order to determine the bifurcation points, one has to solve the nonlinear,
polynomial, algebraic equations  and
and  . For
this reason, one has to use an approximate numerical calculation of the
roots, and the simple Newton-Raphson method will prove to be a good
choice.
. For
this reason, one has to use an approximate numerical calculation of the
roots, and the simple Newton-Raphson method will prove to be a good
choice.
Newton-Raphson’s method uses an initial guess  for the solution of the
equation
for the solution of the
equation  and computes a sequence of points
and computes a sequence of points 




 that presumably converges to one of the roots of the equation.
The computation stops at a finite
that presumably converges to one of the roots of the equation.
The computation stops at a finite  , when we decide that the desired
level of accuracy has been achieved. In order to understand how it works,
we assume that
, when we decide that the desired
level of accuracy has been achieved. In order to understand how it works,
we assume that  is an analytic function for all the values of
is an analytic function for all the values of  used in the computation. Then, by Taylor expanding around
used in the computation. Then, by Taylor expanding around  we
obtain
we
obtain
 | (3.22) |
If we wish to have  , we choose
, we choose
 | (3.23) |
The equation above gives the Newton-Raphson method for one equation
 of one variable
of one variable  . Different choices for
. Different choices for  will possibly lead to
different roots. When
will possibly lead to
different roots. When  ,
,  are non zero at the root and
are non zero at the root and  is
bounded, the convergence of the method is quadratic with the number of
iterations. This means that there is a neighborhood of the root
is
bounded, the convergence of the method is quadratic with the number of
iterations. This means that there is a neighborhood of the root  such that the
distance
such that the
distance  is
is 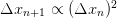 . If the root
. If the root  has multiplicity
larger than 1, convergence is slower. The proofs of these statements are simple and
can be found in [29].
has multiplicity
larger than 1, convergence is slower. The proofs of these statements are simple and
can be found in [29].
The Newton-Raphson method is simple to program and, most of the times,
sufficient for the solution of many problems. In the general case it works well only
close enough to a root. We should also keep in mind that there are simple reasons
for the method to fail. For example, when  for some
for some  , the method
stops. For functions that tend to
, the method
stops. For functions that tend to  as
as 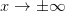 , it is easy to make a bad choice
for
, it is easy to make a bad choice
for  that does not lead to convergence to a root. Sometimes it is a
good idea to combine the Newton-Raphson method with the bisection
method. When the derivative
that does not lead to convergence to a root. Sometimes it is a
good idea to combine the Newton-Raphson method with the bisection
method. When the derivative  diverges at the root we might get into
trouble. For example, the equation
diverges at the root we might get into
trouble. For example, the equation  with
with  , does
not lead to a convergent sequence. In some cases, we might enter into
non-convergent cycles [8]. For some functions the basin of attraction of a root
(the values of
, does
not lead to a convergent sequence. In some cases, we might enter into
non-convergent cycles [8]. For some functions the basin of attraction of a root
(the values of  that will converge to the root) can be tiny. See problem
13.
that will converge to the root) can be tiny. See problem
13.
As a test case of our program, consider the equation
 | (3.24) |
which results from the solution of Schrödinger’s equation for the energy spectrum
of a quantum mechanical particle of mass  in a one dimensional potential well
of depth
in a one dimensional potential well
of depth  and width
and width  . The parameters
. The parameters  and
and
 . Given
. Given  , we solve for
, we solve for  which gives the energy
which gives the energy  . The
function
. The
function  and its derivative
and its derivative  are
are
The program of the Newton-Raphson method for solving the equation  can be found in the file nr.f90:
can be found in the file nr.f90:
!===========================================================
!Newton Raphson for a function of one variable
!===========================================================
program NewtonRaphson
implicit none
real(8), parameter :: rho = 15.0D0
real(8), parameter :: eps = 1D-6
integer, parameter :: NMAX = 1000
real(8) :: x0, x1, err, g, gp
integer :: i
print *, ’Enter x0: ’
read *, x0
err = 1.0D0
print *,’iter x error ’
print *,’-------------------------------------------------’
print *, 0,x0,err
do i=1,NMAX
!value of function g(x):
g = x0*tan(x0)-sqrt(rho*rho-x0*x0)
!value of the derivative g’(x):
gp = x0/sqrt(rho*rho-x0*x0)+x0/(cos(x0)**2)+tan(x0)
x1 = x0 - g/gp
err = ABS(x1-x0)
print *,i,x1,err
if(err .lt. eps) exit
x0 = x1
enddo
end program NewtonRaphson
In the program listed above, the user is asked to set the initial point  . We fix
. We fix
 rho
rho  . It is instructive to make the plot of the left and right hand sides
of (3.24) and make a graphical determination of the roots from their
intersections. Then we can make appropriate choices of the initial point
. It is instructive to make the plot of the left and right hand sides
of (3.24) and make a graphical determination of the roots from their
intersections. Then we can make appropriate choices of the initial point  .
Using gnuplot, the plots are made with the commands:
.
Using gnuplot, the plots are made with the commands:
gnuplot> g1(x) = x*tan(x)
gnuplot> g2(x) = sqrt(rho*rho-x*x)
gnuplot> plot [0:20][0:20] g1(x), g2(x)
The compilation and running of the program can be done as follows:
> gfortran nr.f90 -o n
> echo "1.4"|./n
Enter x0:
iter x error
-------------------------------------------------
0 1.3999999999999999 1.0000000000000000
1 1.5254292024457967 0.12542920244579681
2 1.5009739120496131 2.4455290396183660E-002
3 1.4807207017202200 2.0253210329393090E-002
4 1.4731630533073483 7.5576484128716537E-003
5 1.4724779331237687 6.8512018357957949E-004
6 1.4724731072313519 4.8258924167932093E-006
7 1.4724731069952235 2.3612845012621619E-010
We conclude that one of the roots of the equation is  .
The reader can compute more of these roots by following these steps by
herself.
.
The reader can compute more of these roots by following these steps by
herself.
The method discussed above can be easily generalized to the case of two
equations. Suppose that we need to solve simultaneously two algebraic equations
 and
and  . In order to compute a sequence
. In order to compute a sequence  ,
,
 ,
,  ,
,  ,
,  ,
,  that may converge to a root
of the above system of equations, we Taylor expand the two functions around
that may converge to a root
of the above system of equations, we Taylor expand the two functions around

Defining  and
and  and setting
and setting
 ,
,  , we obtain This is a linear
, we obtain This is a linear  system of equations where
system of equations where  and
and  , with
, with  . Solving for
. Solving for  we obtain
The iterations stop when
we obtain
The iterations stop when  become small enough.
become small enough.
As an example, consider the equations with  ,
,
 . We have
. We have  ,
,  ,
,  ,
,
 . The program can be found in the file nr2.f90:
. The program can be found in the file nr2.f90:
!===========================================================
!Newton Raphson of two functions of two variables
!===========================================================
program NewtonRaphson2
implicit none
real(8), parameter :: eps = 1D-6
integer, parameter :: NMAX = 1000
real(8) :: A(2,2),b(2),dx(2)
real(8) :: x,y, err
integer :: i
print *, ’Enter x0,y0: ’
read *, x,y
err = 1.0D0
print *,’iter x y error ’
print *,’-------------------------------------------------’
print *, 0,x,y,err
do i=1,NMAX
b(1) = -(2.0D0*x*x-3.0D0*x*y+y-2.0D0) ! -g1(x,y)
b(2) = -(3.0D0*x + x*y + y - 1.0D0) ! -g2(x,y)
! dg1/dx dg1/dy
A(1,1) = 4.0D0*x-3.0D0*y; A(1,2) = 1.0D0-3.0D0*x
! dg2/dx dg2/dy
A(2,1) = 3.0D0+y ; A(2,2) = 1.0D0+x
call solve2x2(A,B,dx)
x = x + dx(1)
y = y + dx(2)
err = 0.5D0*SQRT(dx(1)**2+dx(2)**2)
print *,i,x,y,err
if(err .lt. eps) exit
enddo
end program NewtonRaphson2
!===========================================================
subroutine solve2x2(A,b,dx)
implicit none
real(8) :: A(2,2),b(2),dx(2)
real(8) :: num1,num2,det
num1 = A(2,2)*b(1)-A(1,2)*b(2)
num2 = A(1,1)*b(2)-A(2,1)*b(1)
det = A(1,1)*A(2,2)-A(1,2)*A(2,1)
if(det .eq. 0.0D0) stop ’solve2x2: det=0’
dx(1)= num1/det
dx(2)= num2/det
end subroutine solve2x2
In order to guess the region where the real roots of the systems lie, we make a
3-dimensional plot using gnuplot:
gnuplot> set isosamples 20
gnuplot> set hidden3d
gnuplot> splot 2*x**2-3*x*y+y-2,3*x+y*x+y-1,0
We plot the functions  together with the plane
together with the plane  . The intersection
of the three surfaces determine the roots we are looking for. Compiling and
running the program can be done by using the commands:
. The intersection
of the three surfaces determine the roots we are looking for. Compiling and
running the program can be done by using the commands:
> gfortran nr2.f90 -o n
> echo 2.2 1.5 |./n
Enter x0,y0:
iter x y error
--------------------------------------
0 2.20000000 1.50000000 1.0000
1 0.76427104 0.26899383 0.9456
2 0.73939531 -0.68668275 0.4780
3 0.74744506 -0.71105605 1.2834E-002
4 0.74735933 -0.71083147 1.2019E-004
5 0.74735932 -0.71083145 1.2029E-008
> echo 0 1 |./n
.................
5 -0.10899022 1.48928857 4.3461E-012
> echo -5 0|./n
6 -6.13836909 -3.77845711 3.2165E-013
The computation above leads to the roots 
 ,
,

 ,
, 
 .
.
The Newton-Raphson method for many variables becomes hard quite soon:
One needs to calculate the functions as well as their derivatives, which is
prohibitively expensive for many problems. It is also hard to determine the roots,
since the method converges satisfactorily only very close to the roots. We refer
the reader to [8] for more information on how one can deal with these
problems.
3.5 Calculation of the Bifurcation Points
In order to determine the bifurcation points for  we will solve the algebraic
equations
we will solve the algebraic
equations  and
and  . At these points,
. At these points,  -cycles
become unstable and
-cycles
become unstable and  -cycles appear and are stable. This happens when
-cycles appear and are stable. This happens when
 , where
, where  . We will look for solutions
. We will look for solutions  for
for
 .
.
We define the functions  and
and  as in equation (3.6) . We will solve the algebraic equations:
as in equation (3.6) . We will solve the algebraic equations:
According to the discussion of the previous section, in order to calculate the roots
of these equations we have to solve the linear system (3.28) , where the
coefficients are The derivatives will be calculated approximately using finite differences
and similarly for the second derivatives We are now ready to write the program for the Newton-Raphson method like in
the previous section. The only difference is the approximate calculation of the
derivatives using the relations above and the calculation of the function
 by a routine that will compose the function
by a routine that will compose the function 
 -times. The
program can be found in the file bifurcationPoints.f90:
-times. The
program can be found in the file bifurcationPoints.f90:
!===========================================================
! bifurcationPoints.f
! Calculate bifurcation points of the discrete logistic map
! at period k by solving the condition
! g1(x,r) = x - F(k,x,r) = 0
! g2(x,r) = dF(k,x,r)/dx+1 = 0
! determining when the Floquet multiplier becomes 1
! F(k,x,r) iterates F(x,r) = r*x*(x-1) k times
! The equations are solved by using a Newton-Raphson method
!===========================================================
program bifurcationPoints
implicit none
real(8),parameter :: tol=1.0D-10
integer :: k,iter
real(8) :: r0,x0
real(8) :: A(2,2),B(2),dX(2)
real(8) :: error
real(8) :: F,dFdx,dFdr,d2Fdx2,d2Fdrdx
! ---- Input:
print *,’# Enter k,r0,x0:’
read *,k,r0,x0
print *,’# Period k= ’,k
print *,’# r0= ’,r0,’ x0= ’,x0
! ---- Initialize
error = 1.0D0 !initial large value of error>tol
iter = 0
do while(error .gt. tol)
! ---- Calculate jacobian matrix
A(1,1) = 1.0D0-dFdx(k,x0,r0)
A(1,2) = -dFdr (k,x0,r0)
A(2,1) = d2Fdx2 (k,x0,r0)
A(2,2) = d2Fdrdx (k,x0,r0)
B(1) = -x0 + F(k,x0,r0)
B(2) = -dFdx (k,x0,r0)-1.0D0
! ---- Solve a 2x2 linear system:
call solve2x2(A,B,dX)
x0 = x0 + dX(1)
r0 = r0 + dX(2)
error = 0.5D0*sqrt(dX(1)**2+dX(2)**2)
iter = iter+1
print*,iter,’x0= ’,x0,’ r0= ’,r0,’ err=’,error
enddo !do while(error .gt. tol)
end program bifurcationPoints
!===========================================================
!Function F(k,x,r) and its derivatives
real(8) function F(k,x,r)
implicit none
real(8) :: x,r,x0
integer k,i
x0 = x
do i=1,k
x0 = r*x0*(1.0D0-x0)
enddo
F = x0
end function F
! ----------------------------------
real(8) function dFdx(k,x,r)
implicit none
real(8) :: x,r,eps
real(8) :: F
integer k
eps = 1.0D-6*x
dFdx = (F(k,x+eps,r)-F(k,x-eps,r))/(2.0D0*eps)
end function dFdx
! ----------------------------------
real(8) function dFdr(k,x,r)
implicit none
real(8) :: x,r,eps
real(8) :: F
integer k
eps = 1.0D-6*r
dFdr = (F(k,x,r+eps)-F(k,x,r-eps))/(2.0D0*eps)
end function dFdr
! ----------------------------------
real(8) function d2Fdx2(k,x,r)
implicit none
real(8) :: x,r,eps
real(8) :: F
integer k
eps = 1.0D-6*x
d2Fdx2 = (F(k,x+eps,r)-2.0D0*F(k,x,r)+F(k,x-eps,r))/(eps*eps)
end function d2Fdx2
! ----------------------------------
real(8) function d2Fdrdx(k,x,r)
implicit none
real(8) :: x,r,epsx,epsr
real(8) :: F
integer k
epsx = 1.0D-6*x
epsr = 1.0D-6*r
d2Fdrdx = (F(k,x+epsx,r+epsr)-F(k,x+epsx,r-epsr) &
-F(k,x-epsx,r+epsr)+F(k,x-epsx,r-epsr)) &
/(4.0D0*epsx*epsr)
end function d2Fdrdx
!===========================================================
subroutine solve2x2(A,b,dx)
implicit none
real(8) :: A(2,2),b(2),dx(2)
real(8) :: num1,num2,det
num1 = A(2,2)*b(1) - A(1,2)*b(2)
num2 = A(1,1)*b(2) - A(2,1)*b(1)
det = A(1,1)*A(2,2)- A(1,2)*A(2,1)
if(det .eq. 0.0D0) stop ’solve2x2: det = 0’
dx(1) = num1/det
dx(2) = num2/det
end subroutine solve2x2
Compiling and running the program can be done as follows:
> gfortran bifurcationPoints.f90 -o b
> echo 2 3.5 0.5 |./b
# Enter k,r0,x0:
# Period k= 2
# r0= 3.5000000000000 x0= 0.50000000000
1 x0= 0.4455758353187 r0= 3.38523275827 err= 6.35088E-002
2 x0= 0.4396562547624 r0= 3.45290970406 err= 3.39676E-002
3 x0= 0.4399593001407 r0= 3.44949859951 err= 1.71226E-003
4 x0= 0.4399601690333 r0= 3.44948974267 err= 4.44967E-006
5 x0= 0.4399601689937 r0= 3.44948974281 err= 7.22160E-011
> echo 2 3.5 0.85 | ./b
.................
4 x0= 0.8499377795512 r0= 3.44948974275 err= 1.85082E-011
> echo 4 3.5 0.5 |./b
.................
5 x0= 0.5235947861540 r0= 3.54409035953 err= 1.86318E-011
> echo 4 3.5 0.35 | ./b
.................
5 x0= 0.3632903374118 r0= 3.54409035955 err= 5.91653E-013
The above listing shows the points of the 2-cycle and some of the points of the
4-cycle. It is also possible to compare the calculated value  with the expected one
with the expected one 
 . Improving the accuracy
of the calculation is left as an exercise for the reader who has to control the
systematic errors of the calculations and achieve better accuracy in the
computation of
. Improving the accuracy
of the calculation is left as an exercise for the reader who has to control the
systematic errors of the calculations and achieve better accuracy in the
computation of  .
.
3.6 Liapunov Exponents
We have seen that when  , the trajectories of the logistic map
become non periodic and exhibit chaotic behavior. Chaotic behavior mostly
means sensitivity of the evolution of a dynamical system to the choice of initial
conditions. More precisely, it means that two different trajectories constructed
from infinitesimally close initial conditions, diverge very fast from each other. This
implies that there is a set of initial conditions that densely cover subintervals of
, the trajectories of the logistic map
become non periodic and exhibit chaotic behavior. Chaotic behavior mostly
means sensitivity of the evolution of a dynamical system to the choice of initial
conditions. More precisely, it means that two different trajectories constructed
from infinitesimally close initial conditions, diverge very fast from each other. This
implies that there is a set of initial conditions that densely cover subintervals of
 whose trajectories do not approach arbitrarily close to any cycle of finite
length.
whose trajectories do not approach arbitrarily close to any cycle of finite
length.
Assume that two trajectories have  ,
,  as initial points and
as initial points and
 . When the points
. When the points  ,
,  have a distance
have a distance  that for small enough
that for small enough  increases exponentially with
increases exponentially with  (the “time”),
i.e.
(the “time”),
i.e.
 | (3.34) |
the system is most likely exhibiting chaotic
behavior .
The exponent  is called a Liapunov exponent. A useful equation for the
calculation of
is called a Liapunov exponent. A useful equation for the
calculation of  is
is
 | (3.35) |
This relation can be easily proved by considering infinitesimal  so that
so that
 . Then we obtain
. Then we obtain
We can show by induction that  and by
taking the logarithm and the limits we can prove (3.35) .
and by
taking the logarithm and the limits we can prove (3.35) .
A first attempt to calculate the Liapunov exponents could be made by using
the definition (3.34) . We modify the program logistic.f90 so that it calculates
two trajectories whose initial distance is  epsilon:
epsilon:
!===========================================================
!Discrete Logistic Map:
!Two trajectories with close initial conditions.
!===========================================================
program logistic_map
implicit none
integer :: NSTEPS,i
real(8) :: r,x0,x1,x0t,x1t,epsilon
! ----- Input:
print *,’# Enter NSTEPS, r, x0, epsilon:’
read *,NSTEPS,r,x0,epsilon
print *,’# NSTEPS = ’,NSTEPS
print *,’# r = ’,r
print *,’# x0 = ’,x0
print *,’# epsilon = ’,epsilon
x0t = x0+epsilon
! ----- Initialize:
open(unit=33,file=’lia.dat’)
write(33,*) 1,x0,x0t,ABS(x0t-x0)/epsilon
! ----- Calculate:
do i=2,NSTEPS
x1 = r * x0 * (1.0D0-x0 )
x1t = r * x0t * (1.0D0-x0t)
write(33,*)i,x1,x1t,ABS(x1t-x1)/epsilon
x0 = x1; x0t = x1t
enddo
close(33)
end program logistic_map
After running the program, the quantity  is found at the fourth column
of the file lia.dat. The curves of figure 3.7 can be constructed by using the
commands:
is found at the fourth column
of the file lia.dat. The curves of figure 3.7 can be constructed by using the
commands:
> gfortran liapunov1.f90 -o l
> gnuplot
gnuplot> set logscale y
gnuplot> plot \
"<echo 200 3.6 0.2 1e-15 |./l;cat lia.dat" u 1:4 w l
The last line plots the stdout of the command "echo 200 3.6 0.2 1e-15
|./l;cat lia.dat", i.e. the contents of the file lia.dat produced after running
our program using the parameters NSTEPS  , r
, r  , x0
, x0  and
epsilon
and
epsilon  . The gnuplot command set logscale y, puts the y axis
in a logarithmic scale. Therefore an exponential function is shown as a
straight line and this is what we see in figure 3.7: The points
. The gnuplot command set logscale y, puts the y axis
in a logarithmic scale. Therefore an exponential function is shown as a
straight line and this is what we see in figure 3.7: The points  tend to lie on a straight line as
tend to lie on a straight line as  decreases. The slopes of these lines are
equal to the Liapunov exponent
decreases. The slopes of these lines are
equal to the Liapunov exponent  . Deviations from the straight line
behavior indicates corrections and systematic errors, as we point out in figure
3.7. A different initial condition results in a slightly different value of
. Deviations from the straight line
behavior indicates corrections and systematic errors, as we point out in figure
3.7. A different initial condition results in a slightly different value of
 , and the true value can be estimated as the average over several such
choices. We estimate the error of our computation from the standard
error of the mean. The reader should perform such a computation as an
exercise.
, and the true value can be estimated as the average over several such
choices. We estimate the error of our computation from the standard
error of the mean. The reader should perform such a computation as an
exercise.
One can perform a fit of the points  to the exponential function in
the following way: Since
to the exponential function in
the following way: Since 
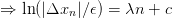 , we can
make a fit to a straight line instead. Using gnuplot, the relevant commands
are:
, we can
make a fit to a straight line instead. Using gnuplot, the relevant commands
are:
gnuplot> fit [5:53] a*x+b \
"<echo 500 3.6 0.2 1e-15 |./l;cat lia.dat"\
using 1:(log($4)) via a,b
gnuplot> replot exp(a*x+b)
The command shown above fits the data to the function a*x+b by taking the 1st
column and the logarithm of the 4th column (using 1:(log($4))) of the
stdout of the command that we used for creating the previous plot. We
choose data for which  ([5:53]) and the fitting parameters
are a,b (via a,b). The second line, adds the fitted function to the plot.
([5:53]) and the fitting parameters
are a,b (via a,b). The second line, adds the fitted function to the plot.
Now we are going to use equation (3.35) for calculating  . This equation is
approximately correct when (a) we have already reached the steady state and (b)
in the large
. This equation is
approximately correct when (a) we have already reached the steady state and (b)
in the large  limit. For this reason we should study if we obtain a satisfactory
convergence when we (a) “throw away” a number of NTRANS steps, (b) calculate
the sum (3.35) for increasing NSTEPS=
limit. For this reason we should study if we obtain a satisfactory
convergence when we (a) “throw away” a number of NTRANS steps, (b) calculate
the sum (3.35) for increasing NSTEPS=  (c) calculate the sum (3.35) for
many values of the initial point
(c) calculate the sum (3.35) for
many values of the initial point  . This has to be carefully repeated
for all values of
. This has to be carefully repeated
for all values of  since each factor will contribute differently to the
quality of the convergence: In regions that manifest chaotic behavior (large
since each factor will contribute differently to the
quality of the convergence: In regions that manifest chaotic behavior (large
 ) convergence will be slower. The program can be found in the file
liapunov2.f90:
) convergence will be slower. The program can be found in the file
liapunov2.f90:
!===========================================================
!Discrete Logistic Map:
!Liapunov exponent from sum_i ln|f’(x_i)|
! NTRANS: number of discarded iteration in order to discard
! transient behavior
! NSTEPS: number of terms in the sum
!===========================================================
program logistic_map
implicit none
integer :: NTRANS,NSTEPS,i
real(8) :: r,x0,x1,sum
! ----- Input:
print *,’# Enter NTRANS,NSTEPS, r, x0:’
read *,NTRANS,NSTEPS,r,x0
print *,’# NTRANS = ’,NTRANS
print *,’# NSTEPS = ’,NSTEPS
print *,’# r = ’,r
print *,’# x0 = ’,x0
do i=1,NTRANS
x1 = r * x0 * (1.0D0-x0 )
x0 = x1
enddo
sum = log(ABS(r*(1.0D0-2.0D0*x0)))
! ----- Initialize:
open(unit=33,file=’lia.dat’)
write(33,*) 1,x0,sum
! ----- Calculate:
do i=2,NSTEPS
x1 = r * x0 * (1.0D0-x0 )
sum = sum + log(ABS(r*(1.0D0-2.0D0*x1)))
write(33,*)i,x1,sum/i
x0 = x1
enddo
close(33)
end program logistic_map
After NTRANS steps, the program calculates NSTEPS times the sum of the terms
 . At each step the sum divided by the number
of steps i is printed to the file lia.dat. Figure 3.6 shows the results
for
. At each step the sum divided by the number
of steps i is printed to the file lia.dat. Figure 3.6 shows the results
for  . This is a point where the system exhibits strong chaotic
behavior and convergence is achieved after we compute a large number
of steps. Using NTRANS
. This is a point where the system exhibits strong chaotic
behavior and convergence is achieved after we compute a large number
of steps. Using NTRANS  and NSTEPS
and NSTEPS  the achieved
accuracy is about
the achieved
accuracy is about  % with
% with  . The
main contribution to the error comes from the different paths followed by
each initial point chosen. The plot can be constructed with the gnuplot
commands:
. The
main contribution to the error comes from the different paths followed by
each initial point chosen. The plot can be constructed with the gnuplot
commands:
> gfortran liapunov2.f90 -o l
> gnuplot
gnuplot> plot \
"<echo 2000 70000 3.8 0.20 |./l;cat lia.dat" u 1:3 w l,\
"<echo 2000 70000 3.8 0.35 |./l;cat lia.dat" u 1:3 w l,\
"<echo 2000 70000 3.8 0.50 |./l;cat lia.dat" u 1:3 w l,\
"<echo 2000 70000 3.8 0.75 |./l;cat lia.dat" u 1:3 w l,\
"<echo 2000 70000 3.8 0.90 |./l;cat lia.dat" u 1:3 w l
The plot command runs the program using the parameters NTRANS  ,
NSTEPS
,
NSTEPS  , r
, r  and x0
and x0  and plots the
results from the contents of the file lia.dat.
and plots the
results from the contents of the file lia.dat.
In order to determine the regions of chaotic behavior we have to study the
dependence of the Liapunov exponent  on the value of
on the value of  . Using our experience
coming from the careful computation of
. Using our experience
coming from the careful computation of 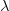 before, we will run the program for
several values of
before, we will run the program for
several values of  using the parameters NTRANS
using the parameters NTRANS  , NSTEPS
, NSTEPS  from the initial point x0
from the initial point x0  . This calculation gives accuracy of the order of
. This calculation gives accuracy of the order of
 %. If we wish to measure
%. If we wish to measure  carefully and estimate the error of the results, we
have to follow the steps described in figures 3.7 and 3.8. The program can be
found in the file liapunov3.f90 and it is a simple modification of the
previous program so that it can perform the calculation for many values of
carefully and estimate the error of the results, we
have to follow the steps described in figures 3.7 and 3.8. The program can be
found in the file liapunov3.f90 and it is a simple modification of the
previous program so that it can perform the calculation for many values of
 .
.
!===========================================================
!Discrete Logistic Map:
!Liapunov exponent from sum_i ln|f’(x_i)|
!Calculation for r in [rmin,rmax] with RSTEPS steps
! RSTEPS: values or r studied: r=rmin+(rmax-rmin)/RSTEPS
! NTRANS: number of discarded iteration in order to discard
! transient behavior
! NSTEPS: number of terms in the sum
! xstart: value of initial x0 for every r
!===========================================================
program logistic_map
implicit none
real(8),parameter :: rmin = 2.5D0
real(8),parameter :: rmax = 4.0D0
real(8),parameter :: xstart = 0.2D0
integer,parameter :: RSTEPS = 1000
integer,parameter :: NSTEPS = 60000
integer,parameter :: NTRANS = 2000
integer :: i,ir
real(8) :: r,x0,x1,sum,dr
open(unit=33,file=’lia.dat’)
dr = (rmax-rmin)/(RSTEPS-1)
do ir=0,RSTEPS-1
r = rmin+ir*dr
x0= xstart
do i=1,NTRANS
x1 = r * x0 * (1.0D0-x0 )
x0 = x1
enddo
sum = log(ABS(r*(1.0D0-2.0D0*x0)))
! ----- Calculate:
do i=2,NSTEPS
x1 = r * x0 * (1.0D0-x0 )
sum = sum + log(ABS(r*(1.0D0-2.0D0*x1)))
x0 = x1
enddo
write(33,*)r,sum/NSTEPS
enddo !do ir=0,RSTEPS-1
close(33)
end program logistic_map
The program can be compiled and run using the commands:
> gfortran liapunov3.f90 -o l
> ./l &
The character & makes the program ./l to run in the background. This is
recommended for programs that run for a long time, so that the shell returns the
prompt to the user and the program continues to run even after the shell is
terminated.
The data are saved in the file lia.dat and we can make the plot shown in
figure 3.7 using gnuplot:
gnuplot> plot "lia.dat" with lines notitle ,0 notitle
Now we can compare figure 3.9 with the bifurcation diagram shown in figure 3.4.
The intervals with  correspond to stable
correspond to stable  -cycles. The intervals where
-cycles. The intervals where
 correspond to manifestation of strong chaos. These intervals are separated
by points with
correspond to manifestation of strong chaos. These intervals are separated
by points with  where the system exhibits weak chaos. This means
that neighboring trajectories diverge from each other with a power law
where the system exhibits weak chaos. This means
that neighboring trajectories diverge from each other with a power law
 instead of an exponential, where
instead of an exponential, where  is
a positive exponent that needs to be determined. The parameter
is
a positive exponent that needs to be determined. The parameter  is
the one usually used in the literature. Strong chaos is obtained in the
is
the one usually used in the literature. Strong chaos is obtained in the
 limit. For larger
limit. For larger  , switching between chaotic and stable periodic
trajectories is observed each time
, switching between chaotic and stable periodic
trajectories is observed each time  changes sign. The critical values
of
changes sign. The critical values
of  can be computed with relatively high accuracy by restricting the
calculation to a small enough neighborhood of the critical point. You can do
this using the program listed above by setting the parameters rmin and
rmax.
can be computed with relatively high accuracy by restricting the
calculation to a small enough neighborhood of the critical point. You can do
this using the program listed above by setting the parameters rmin and
rmax.
We can also study the chaotic properties of the trajectories of the logistic map
by computing the distribution  of the values of
of the values of  in the interval
in the interval  .
After the transitional period, the distribution
.
After the transitional period, the distribution  for the
for the  cycles will have
support only at the points of the
cycles will have
support only at the points of the  cycles, whereas for the chaotic regimes it will
have support on subintervals of
cycles, whereas for the chaotic regimes it will
have support on subintervals of  . The distribution function
. The distribution function  is
independent for most of the initial points of the trajectories. If one obtains a large
number of points from many trajectories of the logistic map, it will be
practically impossible to understand that these are produced by a deterministic
rule. For this reason, chaotic systems can be used for the production of
pseudorandom numbers, as we will see in chapter 11. By measuring the
entropy, which is a measure of disorder in a system, we can quantify the
“randomness” of the distribution. As we will see in chapter 12, it is given by the
equation
is
independent for most of the initial points of the trajectories. If one obtains a large
number of points from many trajectories of the logistic map, it will be
practically impossible to understand that these are produced by a deterministic
rule. For this reason, chaotic systems can be used for the production of
pseudorandom numbers, as we will see in chapter 11. By measuring the
entropy, which is a measure of disorder in a system, we can quantify the
“randomness” of the distribution. As we will see in chapter 12, it is given by the
equation
 | (3.37) |
where  is the probability of observing the state
is the probability of observing the state  . In our case, we can make
an approximate calculation of
. In our case, we can make
an approximate calculation of  by dividing the interval
by dividing the interval  to
to  subintervals of width
subintervals of width  . For given
. For given  we obtain a large number
we obtain a large number  of values
of values
 of the logistic map and we compute the histogram
of the logistic map and we compute the histogram  of their distribution in
the intervals
of their distribution in
the intervals  . The probability density is obtained from the limit
of
. The probability density is obtained from the limit
of  as
as  becomes large and
becomes large and  small (large
small (large  ).
Indeed,
).
Indeed,  converges to
converges to  . We will define
. We will define
 .
.
The program listed below calculates  for chosen values of
for chosen values of  , and then the
entropy
, and then the
entropy  is calculated using (3.37) . It is a simple modification of the
program in liapunov3.f90 where we add the parameter NHIST counting the
number of intervals
is calculated using (3.37) . It is a simple modification of the
program in liapunov3.f90 where we add the parameter NHIST counting the
number of intervals  for the histograms. The probability density is
calculated in the array p(NHIST). The program can be found in the file
entropy.f90:
for the histograms. The probability density is
calculated in the array p(NHIST). The program can be found in the file
entropy.f90:
!===========================================================
!Discrete Logistic Map:
!Entropy calculation from S=-sum_i p_i ln p_i
!Calculation for r in [rmin,rmax] with RSTEPS steps
! RSTEPS: values or r studied: r=rmin+(rmax-rmin)/RSTEPS
! NHIST : number of histogram bins for calculation of p_i
! NSTEPS: number of values of x in the histograms
! NTRANS: number of discarted iteration in order to discard
! transient behavior
! xstart: value of initial x0 for every r
!===========================================================
program logistic_map
implicit none
real(8),parameter :: rmin = 2.5D0
real(8),parameter :: rmax = 4.0D0
real(8),parameter :: xstart = 0.2D0
integer,parameter :: RSTEPS = 1000
integer,parameter :: NHIST = 10000
integer,parameter :: NTRANS = 2000
integer,parameter :: NSTEPS = 5000000
real(8),parameter :: xmin=0.0D0,xmax=1.0D0
integer :: i,ir,isum,n
real(8) :: r,x0,x1,sum,dr,dx
real(8) :: p(NHIST),S
open(unit=33,file=’entropy.dat’)
p = 0.0D0
dr = (rmax-rmin)/(RSTEPS-1)
dx = (xmax-xmin)/(NHIST -1)
do ir=0,RSTEPS-1
r = rmin+ir*dr
x0= xstart
do i=1,NTRANS
x1 = r * x0 * (1.0D0-x0 )
x0 = x1
enddo
!make histogram:
n=INT(x0/dx)+1;p(n)=p(n)+1.0D0
do i=2,NSTEPS
x1 = r * x0 * (1.0D0-x0 )
n = INT(x1/dx)+1
p(n)=p(n)+1.0D0
x0 = x1
enddo
!p(k) is now histogram of x-values.
!Normalize so that sum_k p(k)*dx=1
!to get probability distribution:
p = p/NSTEPS/dx
!sum all non zero terms: p(n)*log(p(n))*dx
S = -SUM(p*log(p),MASK=p.gt.0.0D0)*dx
write(33,*)r,S
enddo !do ir=0,RSTEPS-1
close(33)
!print the last probability distribution:
open(unit=34,file=’entropy_hist.dat’)
do n=1,NHIST
x0 = xmin +(n-1)*dx + 0.5D0*dx
write(34,*) r,x0,p(n)
enddo
close(34)
end program logistic_map
For the calculation of the distribution functions and the entropy we have to
choose the parameters which control the systematic error. The parameter NTRANS
should be large enough so that the transitional behavior will not contaminate our
results. Our measurements must be checked for being independent of its value.
The same should be done for the initial point xstart. The parameter
NHIST controls the partitioning of the interval  and the width
and the width  ,
so it should be large enough. The parameter NSTEPS is the number of
“measurements” for each value of
,
so it should be large enough. The parameter NSTEPS is the number of
“measurements” for each value of  and it should be large enough in
order to reduce the “noise” in
and it should be large enough in
order to reduce the “noise” in  . It is obvious that NSTEPS should be
larger when
. It is obvious that NSTEPS should be
larger when  becomes smaller. Appropriate choices lead to the plots
shown in figures 3.10 and 3.11 for
becomes smaller. Appropriate choices lead to the plots
shown in figures 3.10 and 3.11 for  ,
,  and
and  . We see that
stronger chaotic behavior means a wider distribution of the values of
. We see that
stronger chaotic behavior means a wider distribution of the values of
 .
.
The entropy is shown in figure 3.12. The stable periodic trajectories lead to
small entropy, whereas the chaotic ones lead to large entropy. There is a sudden
increase in the value of the entropy at the beginning of chaos at  , which
increases even further as the chaotic behavior becomes stronger. During the
intermissions of the chaotic behavior there are sudden drops in the value of the
entropy. It is quite instructive to compare the entropy diagrams with the
corresponding bifurcation diagrams (see figure 3.4) and the Liapunov
exponent diagrams (see figure 3.9). The entropy is increasing until
, which
increases even further as the chaotic behavior becomes stronger. During the
intermissions of the chaotic behavior there are sudden drops in the value of the
entropy. It is quite instructive to compare the entropy diagrams with the
corresponding bifurcation diagrams (see figure 3.4) and the Liapunov
exponent diagrams (see figure 3.9). The entropy is increasing until  reaches its maximum value 4, but this is not done smoothly. By magnifying
the corresponding areas in the plot, we can see an infinite number of
sudden drops in the entropy in intervals of
reaches its maximum value 4, but this is not done smoothly. By magnifying
the corresponding areas in the plot, we can see an infinite number of
sudden drops in the entropy in intervals of  that become more and more
narrow.
that become more and more
narrow.
3.7 Problems
Several of the programs that you need to write for solving the problems of this
chapter can be found in the Problems directory of the accompanying software of
this chapter.
- Confirm that the trajectories of the logistic map for
 are falling off
exponentially for large enough
are falling off
exponentially for large enough  .
.
- Choose
 and plot the trajectories for
and plot the trajectories for  with
step
with
step  for
for  . Put the
. Put the  axis in a logarithmic
scale. From the resulting curves discuss whether you obtain an
exponential falloff.
axis in a logarithmic
scale. From the resulting curves discuss whether you obtain an
exponential falloff.
- Fit the points
 for
for  to the function
to the function  and determine
the fitting parameters
and determine
the fitting parameters  and
and  . How do these parameters depend on
the initial point
. How do these parameters depend on
the initial point  ? You can use the following gnuplot commands for
your calculation:
? You can use the following gnuplot commands for
your calculation:
gnuplot> !gfortran logistic.f90 -o l
gnuplot> a=0.7;c=0.4;
gnuplot> fit [10:] c*exp(-a*x) \
"<echo 1000 0.5 0.5|./l;cat log.dat" via a,c
gnuplot> plot c*exp(-a*x),\
"<echo 1000 0.5 0.5|./l;cat log.dat" w l
As you can see, we set NSTEPS = 1000, r = 0.5, x0 = 0.5. By
setting the limits [10:] to the fit command, the fit includes
only the points  , therefore avoiding the transitional
period and the deviation from the exponential falloff for small
, therefore avoiding the transitional
period and the deviation from the exponential falloff for small
 .
.
- Repeat for
 with step
with step  and for
and for  . As
you will be approaching
. As
you will be approaching  , you will need to discard more
points from near the origin. You might also need to increase
NSTEPS. You should always check graphically whether the fitted
exponential function is a good fit to the points
, you will need to discard more
points from near the origin. You might also need to increase
NSTEPS. You should always check graphically whether the fitted
exponential function is a good fit to the points  for large
for large
 . Construct a table for the values of
. Construct a table for the values of  as a function of
as a function of
 .
.
The solutions of the equation (3.3) is  . How is this related to the
values that you computed in your table?
. How is this related to the
values that you computed in your table?
- Consider the logistic map for
 . Choose NSTEPS=100 and calculate the
corresponding trajectories for x0=0.2, 0.3, 0.5, 0.7, 0.9. Plot
them on the same graph. Calculate the fixed point
. Choose NSTEPS=100 and calculate the
corresponding trajectories for x0=0.2, 0.3, 0.5, 0.7, 0.9. Plot
them on the same graph. Calculate the fixed point  and compare
your result to the known value
and compare
your result to the known value  . Repeat for x0=
. Repeat for x0=  for
for
 . What do you conclude about the point
. What do you conclude about the point
 ?
?
- Consider the logistic map for
 . Calculate the stable
point
. Calculate the stable
point  and compare your result to the known value
and compare your result to the known value  .
How large should NSTEPS be chosen each time? You may choose
x0=0.3.
.
How large should NSTEPS be chosen each time? You may choose
x0=0.3.
- Consider the logistic map for
 . Take x0=0.3, 0.5, 0.9 and
NSTEPS=300 and plot the resulting trajectories. Calculate the fixed points
. Take x0=0.3, 0.5, 0.9 and
NSTEPS=300 and plot the resulting trajectories. Calculate the fixed points
 and
and  by using the command tail log.dat. Increase NSTEPS and
repeat so that you make sure that the trajectory has converged to the
2-cycle. Compare their values to the ones given by equation (3.18) . Make
the following plots:
by using the command tail log.dat. Increase NSTEPS and
repeat so that you make sure that the trajectory has converged to the
2-cycle. Compare their values to the ones given by equation (3.18) . Make
the following plots:
gnuplot> plot \
"<echo 300 3.2 0.3|./l;awk ’NR%2==0’ log.dat" w l
gnuplot> replot \
"<echo 300 3.2 0.3|./l;awk ’NR%2==1’ log.dat" w l
What do you observe?
- Repeat the previous problem for
 . How big should NSTEPS be
chosen so that you obtain
. How big should NSTEPS be
chosen so that you obtain  and
and  with an accuracy of 6 significant
digits?
with an accuracy of 6 significant
digits?
- Repeat the previous problem for
 and
and  . Choose NSTEPS =
1000, x0 = 0.5. Show that the trajectories approach a 4-cycle
and an 8-cycle respectively. Calculate the fixed points
. Choose NSTEPS =
1000, x0 = 0.5. Show that the trajectories approach a 4-cycle
and an 8-cycle respectively. Calculate the fixed points  -
- and
and
 -
- .
.
- Plot the functions
 ,
,  ,
,  ,
,  for given
for given  on the same
graph. Use the commands:
on the same
graph. Use the commands:
gnuplot> set samples 1000
gnuplot> f(x) = r*x*(1-x)
gnuplot> r=1;plot [0:1] x,f(x),f(f(x)),f(f(f(f(x))))
The command r=1 sets the value of  . Take
. Take  ,
,  ,
,  ,
,  ,
,
 . Determine the fixed points and the
. Determine the fixed points and the  -cycles from the intersections of
the plots with the diagonal
-cycles from the intersections of
the plots with the diagonal  .
.
- Construct the cobweb plots of figures 3.2 and 3.4 for
 and
and  .
Repeat by dropping from the plot an increasing number of initial points, so
that in the end only the
.
Repeat by dropping from the plot an increasing number of initial points, so
that in the end only the  -cycles will remain. Do the same for
-cycles will remain. Do the same for
 .
.
- Construct the bifurcation diagrams shown in figure 3.4.
- Construct the bifurcation diagram of the logistic map for
 and for
and for  . Compute the first four bifurcation points with
an accuracy of 5 significant digits by magnifying the appropriate parts of the
plots. Take NTRANS=15000.
. Compute the first four bifurcation points with
an accuracy of 5 significant digits by magnifying the appropriate parts of the
plots. Take NTRANS=15000.
- Construct the bifurcation diagram of the logistic map for
 .
Compute graphically the bifurcation points
.
Compute graphically the bifurcation points  for
for 





 . Make sure that your results are stable against variations of the
parameters NTRANS, NSTEPS as well as from the choice of branching
point. From the known values of
. Make sure that your results are stable against variations of the
parameters NTRANS, NSTEPS as well as from the choice of branching
point. From the known values of  for
for  , and from the
dependence of your results on the choices of NTRANS, NSTEPS, estimate the
accuracy achieved by this graphical method. Compute the ratios
, and from the
dependence of your results on the choices of NTRANS, NSTEPS, estimate the
accuracy achieved by this graphical method. Compute the ratios
 and compare your results to equation (3.20)
.
and compare your results to equation (3.20)
.
- Choose the values of
 in equation (3.24) so that you obtain only one
energy level. Compute the resulting value of the energy. When do we have
three energy levels?
in equation (3.24) so that you obtain only one
energy level. Compute the resulting value of the energy. When do we have
three energy levels?
- Consider the polynomial
 . Find the
roots obtained by the Newton-Raphson method when you choose
. Find the
roots obtained by the Newton-Raphson method when you choose




 .
What do you conclude concerning the basins of attraction of each root of the
polynomial? Make a plot of the polynomial in a neighborhood of its roots
and try other initial points that will converge to each one of the roots.
.
What do you conclude concerning the basins of attraction of each root of the
polynomial? Make a plot of the polynomial in a neighborhood of its roots
and try other initial points that will converge to each one of the roots.
- Use the Newton-Raphson method in order to compute the 4-cycle
 of the logistic map. Use appropriate areas of the bifurcation
diagram so that you can choose the initial points correctly. Check that
your result for
of the logistic map. Use appropriate areas of the bifurcation
diagram so that you can choose the initial points correctly. Check that
your result for  is the same for all
is the same for all  . Tune the parameters
chosen in your calculation on order to improve the accuracy of your
measurements.
. Tune the parameters
chosen in your calculation on order to improve the accuracy of your
measurements.
- Repeat the previous problem for the 8-cycle
 and
and  .
.
- Repeat the previous problem for the 16-cycle
 and
and  .
.
- Calculate the critical points
 for
for  of the logistic map
using the Newton-Raphson method. In order to achieve that, you should
determine the bifurcation points graphically in the bifurcation diagram first
and then choose the initial points in the Newton-Raphson method
appropriately. The program in bifurcationPoints.f90 should read
the parameters eps, epsx, epsr from the stdin so that they can
be tuned for increasing
of the logistic map
using the Newton-Raphson method. In order to achieve that, you should
determine the bifurcation points graphically in the bifurcation diagram first
and then choose the initial points in the Newton-Raphson method
appropriately. The program in bifurcationPoints.f90 should read
the parameters eps, epsx, epsr from the stdin so that they can
be tuned for increasing  . If these parameters are too small the
convergence will be unstable and if they are too large you will have large
systematic errors. Using this method, try to reproduce table 3.1
. If these parameters are too small the
convergence will be unstable and if they are too large you will have large
systematic errors. Using this method, try to reproduce table 3.1
Table 3.1: The values of  for the logistic map calculated for problem 17.
for the logistic map calculated for problem 17.
 is taken from the bibliography.
is taken from the bibliography.
- Calculate the ratios
 of equation (3.20) using the results of
table 3.1. Calculate Feigenbaum’s constant and comment on the accuracy
achieved by your calculation.
of equation (3.20) using the results of
table 3.1. Calculate Feigenbaum’s constant and comment on the accuracy
achieved by your calculation.
- Estimate Feigenbaum’s constant
 and the critical value
and the critical value  by
assuming that for large enough
by
assuming that for large enough  ,
,  . This behavior
is a result of equation (3.20) . Fit the results of table 3.1 to this
function and calculate
. This behavior
is a result of equation (3.20) . Fit the results of table 3.1 to this
function and calculate  and
and  . This hypothesis is confirmed in
figure 3.13 where we can observe the exponential convergence of
. This hypothesis is confirmed in
figure 3.13 where we can observe the exponential convergence of
 to
to  . Construct the same plot using the parameters of your
calculation.
. Construct the same plot using the parameters of your
calculation.
Hint: You can use the following gnuplot commands:
gnuplot> nmin=2;nmax=17
gnuplot> r(x)= rc-c*d**(-x)
gnuplot> fit [nmin:nmax] r(x) "rcrit" u 1:2 via rc,c,d
gnuplot> plot "rcrit", r(x)
gnuplot> print rc,d
The file rcrit contains the values of table 3.1. You should vary the
parameters nmin, nmax and repeat until you obtain a stable fit.
- Use the Newton-Raphson method to calculate the first three bifurcation
points after the appearance of the 3-cycle for
 . Choose one
bifurcation point of the 3-cycle, one of the 6-cycle and one of the 12-cycle
and magnify the bifurcation diagram in their neighborhood.
. Choose one
bifurcation point of the 3-cycle, one of the 6-cycle and one of the 12-cycle
and magnify the bifurcation diagram in their neighborhood.
- Consider the map describing the evolution of a population
 | (3.38) |
- Plot the functions
 ,
,  ,
,  ,
,  for
for  ,
,
 ,
,  ,
, 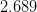 for
for  . For which values of
. For which values of  do you
expect to obtain stable
do you
expect to obtain stable  -cycles?
-cycles?
- For the same values of
 plot the trajectories with initial points
plot the trajectories with initial points
 . For each
. For each  make a separate plot.
make a separate plot.
- Use the Newton-Raphson method in order to determine the points
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
- Construct the bifurcation diagram for
 . Determine
the point marking the onset of chaos as well as the point where
the 3-cycle starts. Magnify the diagram around a branch that you
will choose.
. Determine
the point marking the onset of chaos as well as the point where
the 3-cycle starts. Magnify the diagram around a branch that you
will choose.
- Estimate Feigenbaum’s constant
 as in problem 17. Is your
result compatible with the expectation of universality for the value
of
as in problem 17. Is your
result compatible with the expectation of universality for the value
of  ? Is the value of
? Is the value of  the same as that of the logistic map?
the same as that of the logistic map?
- Consider the sine map:
 | (3.39) |
- Plot the functions
 ,
,  ,
,  ,
,  ,
,  for
for
 ,
,  ,
,  ,
,  ,
,  . Which values of
. Which values of  are
expected to lead to stable
are
expected to lead to stable  -cycles?
-cycles?
- For the same values of
 , plot the trajectories with initial points
, plot the trajectories with initial points
 . Make one plot for each
. Make one plot for each  .
.
- Use the Newton-Raphson method in order to determine the points
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
- Construct the bifurcation diagram for
 . Within which
limits do the values of
. Within which
limits do the values of  lie in? Repeat for
lie in? Repeat for  . What
do you observe? Determine the point marking the onset of chaos
as well as the point where the 3-cycle starts. Magnify the diagram
around a branch that you will choose.
. What
do you observe? Determine the point marking the onset of chaos
as well as the point where the 3-cycle starts. Magnify the diagram
around a branch that you will choose.
- Consider the map:
 | (3.40) |
- Construct the bifurcation diagram for
 . Within which
limits do the values of
. Within which
limits do the values of  lie in? Determine the point marking
the onset of chaos as well as the point where the 3-cycle starts.
Magnify the diagram around a branch that you will choose.
lie in? Determine the point marking
the onset of chaos as well as the point where the 3-cycle starts.
Magnify the diagram around a branch that you will choose.
- Use the Newton-Raphson method in order to determine the points
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
- Consider the tent map:
 | (3.41) |
Construct the bifurcation diagram for  . Within which limits do
the values of
. Within which limits do
the values of  lie in? On the same graph, plot the functions
lie in? On the same graph, plot the functions  ,
,
 .
.
Magnify the diagram in the area  and
and  .
At which point do the two disconnected intervals within which
.
At which point do the two disconnected intervals within which  take their values merge into one? Magnify the areas
take their values merge into one? Magnify the areas  ,
,
 and
and  ,
,  and determine the merging points of two disconnected intervals within
which
and determine the merging points of two disconnected intervals within
which  take their values.
take their values.
- Consider the Gauss map (or mouse map):
 | (3.42) |
Construct the bifurcation diagram for  and
and 

 . Make your program to take as the initial point of the new
trajectory to be the last one of the previous trajectory and choose
. Make your program to take as the initial point of the new
trajectory to be the last one of the previous trajectory and choose
 for
for  . Repeat for
. Repeat for  . What do you
observe? Note that as
. What do you
observe? Note that as  is increased, we obtain bifurcations and
“anti-bifurcations”.
is increased, we obtain bifurcations and
“anti-bifurcations”.
- Consider the circle map:
![xn+1 = [xn + r − q sin(2πxn )] mod1.](main_latex1416x.png) | (3.43) |
(Make sure that your program keeps the values of  so that
so that  ).
Construct the bifurcation diagram for
).
Construct the bifurcation diagram for  and
and  .
.
- Use the program in liapunov.f90 in order to compute the distance between
two trajectories of the logistic map for
 that originally are at a
distance
that originally are at a
distance  . Choose
. Choose 





 and calculate the Liapunov exponent by fitting
to a straight line appropriately. Compute the mean value and the standard
error of the mean.
and calculate the Liapunov exponent by fitting
to a straight line appropriately. Compute the mean value and the standard
error of the mean.
- Calculate the Liapunov exponent for




 for the logistic map. Use both ways mentioned in the text. Choose at least 5
different initial points and calculate the mean and the standard error of the
mean of your results. Compare the values of
for the logistic map. Use both ways mentioned in the text. Choose at least 5
different initial points and calculate the mean and the standard error of the
mean of your results. Compare the values of  that you obtain with each
method and comment.
that you obtain with each
method and comment.
- Compute the critical value
 numerically as the limit
numerically as the limit  for the
logistic map with an accuracy of nine significant digits. Use the
calculation of the Liapunov exponent
for the
logistic map with an accuracy of nine significant digits. Use the
calculation of the Liapunov exponent  given by equation (3.35)
.
given by equation (3.35)
.
- Compute the values of
 of the logistic map numerically for which
we (a) enter a stable 3-cycle (b) reenter into the chaotic behavior.
Do the calculation by computing the Liapunov exponent
of the logistic map numerically for which
we (a) enter a stable 3-cycle (b) reenter into the chaotic behavior.
Do the calculation by computing the Liapunov exponent  and
compare your results with the ones obtained from the bifurcation
diagram.
and
compare your results with the ones obtained from the bifurcation
diagram.
- Calculate the Liapunov exponent using equation (3.35) for the following
maps: and construct the diagrams similar to the ones in figure 3.9. Compare your
plots with the respective bifurcation diagrams (you may put both graphs on
the same plot). Use two different initial points
 for the Gauss
map (
for the Gauss
map (
 ) and observe the differences. For the circle map
(
) and observe the differences. For the circle map
(
![[xn + 1 ∕3 − qsin(2πxn )] mod1](main_latex1446x.png) ) study carefully the values
) study carefully the values
 .
.
- Reproduce the plots in figures 3.10, 3.11 and 3.12. Compute the function
 for
for  ,
,  ,
,  and
and  . Determine the points where
you have stronger chaos by observing
. Determine the points where
you have stronger chaos by observing  and the corresponding values of
the entropy. Compute the entropy for
and the corresponding values of
the entropy. Compute the entropy for  by taking
RSTEPS=2000 and estimate the values of
by taking
RSTEPS=2000 and estimate the values of  where we enter to and exit from
chaos. Compare your results with the computation of the Liapunov
exponent.
where we enter to and exit from
chaos. Compare your results with the computation of the Liapunov
exponent.
- Consider the Hénon map:
- Construct the two bifurcation diagrams for
 and
and  for
for
 ,
, 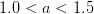 . Check if the values
. Check if the values  that
we will use below correspond to stable periodic trajectories or
chaotic behavior.
that
we will use below correspond to stable periodic trajectories or
chaotic behavior.
- Write a program in a file attractor.f90 which will take NINIT
= NL
 NL initial conditions
NL initial conditions 
 NL on a
NL
NL on a
NL NL lattice of the square
NL lattice of the square  ,
,  .
Each of the points
.
Each of the points  will evolve according to equation
(3.45) for
will evolve according to equation
(3.45) for  NSTEPS steps. The program will print the
points
NSTEPS steps. The program will print the
points  to the stdout. Choose
to the stdout. Choose  ,
,
 , NL
, NL .
.
- Choose
 ,
,  and plot the points
and plot the points  for
for









 on the same
diagram.
on the same
diagram.
- Choose
 ,
,  and plot the points
and plot the points  for
for
 on the same diagram.
on the same diagram.
- Choose
 ,
,  and plot the points
and plot the points  for
for
 on the same diagram. Observe the Hénon strange
attractor and its fractal properties. It is characterized by a
Hausdorff
dimension
on the same diagram. Observe the Hénon strange
attractor and its fractal properties. It is characterized by a
Hausdorff
dimension  . Then magnify the regions
. Then magnify the regions
- Consider the Duffing map:
- Construct the two bifurcation diagrams for
 and
and  for
for
 ,
,  . Choose four different initial conditions
. Choose four different initial conditions

 . What do you observe?
. What do you observe?
- Use the program attractor.f90 from problem 33 in order to
study the attractor of the map for
 ,
,  .
.
- Consider the Tinkerbell map:
- Choose
 ,
, 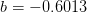 ,
,  ,
,  . Plot a
trajectory on the plane by plotting the points
. Plot a
trajectory on the plane by plotting the points  for
for
 with
with  .
.
- Use the program attractor.f90 from problem 33 in order to
study the attractor of the map for the values of the parameters
 ,
,  ,
,  ,
,  given above. Choose
given above. Choose  ,
,  ,
,
 ,
,  ,
,  .
.
- Repeat the previous question by taking
 .
.
Chapter 4
Motion of a Particle
In this chapter we will study the numerical solution of classical equations of
motion of one dimensional mechanical systems, e.g. a point particle moving on the
line, the simple pendulum etc. We will make an introduction to the numerical
integration of ordinary differential equations with initial conditions and in
particular to the Euler and Runge-Kutta methods. We study in detail the
examples of the damped harmonic oscillator and of the damped pendulum under
the influence of an external periodic force. The latter system is nonlinear and
exhibits interesting chaotic behavior.
4.1 Numerical Integration of Newton’s Equations
Consider the problem of the solution of the dynamical equations of motion of one
particle under the influence of a dynamical field given by Newton’s law. The
equations can be written in the form
 | (4.1) |
where
 | (4.2) |
From the numerical analysis point of view, the problems that we will discuss are
initial value problems for ordinary differential equations where the initial
conditions
 | (4.3) |
determine a unique solution  . The equations (4.1) are of second order with
respect to time and it is convenient to write them as a system of twice as many
first order equations:
. The equations (4.1) are of second order with
respect to time and it is convenient to write them as a system of twice as many
first order equations:
 | (4.4) |
In particular, we will be interested in the study of the motion of a particle
moving on a line (1 dimension), therefore the above equations become
When the particle moves on the plane (2 dimensions) the equations of motion
become
4.2 Prelude: Euler Methods
As a first attempt to tackle the problem, we will study a simple pendulum of
length  in a homogeneous gravitational field
in a homogeneous gravitational field  (figure 4.1).
(figure 4.1).
The equations of motion are given by the differential equations
which can be rewritten as a first order system of differential equations
The equations above need to be written in a discrete form
appropriate for a numerical solution with the aid of a computer. We
split the interval of time of integration ![[ti,tf]](main_latex1549x.png) to
to  equal
intervals
of width
equal
intervals
of width  , where
, where  . The derivatives are
approximated by the relations
. The derivatives are
approximated by the relations  , so that where
, so that where  is the angular acceleration. This is the so-called
Euler method. The error at each step is estimated to be of order
is the angular acceleration. This is the so-called
Euler method. The error at each step is estimated to be of order  .
This is most easily seen by Taylor expanding around the point
.
This is most easily seen by Taylor expanding around the point  and neglecting all terms starting from the second derivative and
beyond .
What we are mostly interested in is in the total error of the estimate of the
functions we integrate for at time
and neglecting all terms starting from the second derivative and
beyond .
What we are mostly interested in is in the total error of the estimate of the
functions we integrate for at time  ! We expect that errors accumulate in an
additive way at each integration step, and since the number of steps is
! We expect that errors accumulate in an
additive way at each integration step, and since the number of steps is
 the total error should be
the total error should be  . This is indeed
what happens, and we say that Euler’s method is a first order method. Its range
of applicability is limited and we only study it for academic reasons. Euler’s
method is asymmetric because it uses information only from the beginning of the
integration interval
. This is indeed
what happens, and we say that Euler’s method is a first order method. Its range
of applicability is limited and we only study it for academic reasons. Euler’s
method is asymmetric because it uses information only from the beginning of the
integration interval  . It can be put in a more balanced form by using
the velocity at the end of the interval
. It can be put in a more balanced form by using
the velocity at the end of the interval  . This way we obtain the
Euler-Cromer method with a slightly improved behavior, but which is still of first
order
. This way we obtain the
Euler-Cromer method with a slightly improved behavior, but which is still of first
order
An improved algorithm is the Euler–Verlet method which is of second order and gives
total error
 . This is given by the equations
. This is given by the equations
The price that we have to pay is that we have to use a two step relation in
order to advance the solution to the next step. This implies that we have to
carefully determine the initial conditions of the problem which are given only at
one given time  . We make one Euler time step backwards in order to define the
value of
. We make one Euler time step backwards in order to define the
value of  . If the initial conditions are
. If the initial conditions are  ,
,  , then we
define
, then we
define
 | (4.12) |
It is important that at this step the error introduced is not larger than  ,
otherwise it will spoil and eventually dominate the
,
otherwise it will spoil and eventually dominate the  total error of the
method introduced by the intermediate steps. At the last step we also have to
take
total error of the
method introduced by the intermediate steps. At the last step we also have to
take
 | (4.13) |
Even though the method has smaller total error than the Euler method, it
becomes unstable for small enough  due to roundoff errors. In particular, the
second equation in (4.11) gives the angular velocity as the ratio of two small
numbers. The problem is that the numerator is the result of the subtraction of
two almost equal numbers. For small enough
due to roundoff errors. In particular, the
second equation in (4.11) gives the angular velocity as the ratio of two small
numbers. The problem is that the numerator is the result of the subtraction of
two almost equal numbers. For small enough  , this difference has to be
computed from the last digits of the finite representation of the numbers
, this difference has to be
computed from the last digits of the finite representation of the numbers  and
and  in the computer memory. The accuracy in the determination of
in the computer memory. The accuracy in the determination of
 decreases until it eventually becomes exactly zero. For the first
equation of (4.11) , the term
decreases until it eventually becomes exactly zero. For the first
equation of (4.11) , the term  is smaller by a factor
is smaller by a factor  compared to the
term
compared to the
term  in Euler’s method. At some point, by decreasing
in Euler’s method. At some point, by decreasing  , we obtain
, we obtain
 and the accuracy of the method vanishes due to the finite
representation of real number in the memory of the computer. When the
numbers
and the accuracy of the method vanishes due to the finite
representation of real number in the memory of the computer. When the
numbers  and
and  differ from each other by more that
approximately seven orders of magnitude, adding the first one to the
second is equivalent to adding zero and the contribution of the acceleration
vanishes .
differ from each other by more that
approximately seven orders of magnitude, adding the first one to the
second is equivalent to adding zero and the contribution of the acceleration
vanishes .
Writing programs that implement the methods discussed so far is quite simple.
We will write a program that compares the results from all three methods
Euler, Euler–Cromer and Euler–Verlet. The main program is mainly a
user interface, and the computation is carried out by three subroutines
euler, euler_cromer and euler_verlet. The user must provide the
function accel(x) which gives the angular acceleration as a function of
x. The variable x in our problem corresponds to the angle  . For
starters we take accel(x)= -10.0 * sin(x), the acceleration of the simple
pendulum.
. For
starters we take accel(x)= -10.0 * sin(x), the acceleration of the simple
pendulum.
The data structure is very simple: Three real arrays REAL T(P), X(P) and
V(P) store the times  , the angles
, the angles  and the angular velocities
and the angular velocities  for
for
 . The user determines the time interval for the integration from
. The user determines the time interval for the integration from
 to
to  and the number of discrete times Nt. The latter should be
less than P, the size of the arrays. She also provides the initial conditions
and the number of discrete times Nt. The latter should be
less than P, the size of the arrays. She also provides the initial conditions
 and
and  . After this, we call the main integration routines which
take as input the initial conditions, the time interval of the integration and the
number of discrete times Xin,Vin,Tfi,Nt. The output of the routines is the
arrays T,X,V which store the results for the time, position and velocity
respectively. The results are printed to the files euler.dat, euler_cromer.dat
and euler_verlet.dat.
. After this, we call the main integration routines which
take as input the initial conditions, the time interval of the integration and the
number of discrete times Xin,Vin,Tfi,Nt. The output of the routines is the
arrays T,X,V which store the results for the time, position and velocity
respectively. The results are printed to the files euler.dat, euler_cromer.dat
and euler_verlet.dat.
After setting the initial conditions and computing the time step
 , the integration in each of the subroutines is performed
in do loops which advance the solution for time
, the integration in each of the subroutines is performed
in do loops which advance the solution for time  . The results are stored at
each step in the arrays T,X,V. For example, the central part of the program for
Euler’s method is:
. The results are stored at
each step in the arrays T,X,V. For example, the central part of the program for
Euler’s method is:
T(1) = 0.0
X(1) = Xin
V(1) = Vin
h = Tfi/(Nt-1)
do i = 2,Nt
T(i) = T(i-1)+h
X(i) = X(i-1)+V(i-1)*h
V(i) = V(i-1)+accel(X(i-1))*h
enddo
Some care has to be taken in the case of the Euler–Verlet method where one has
to initialize the first two steps, as well as take special care for the last step for the
velocity:
T(1) = 0.0
X(1) = Xin
V(1) = Vin
X0 = X(1) - V(1) * h + accel(X(1)) *h*h/2.0
T(2) = h
X(2) = 2.0*X(1) - X0 + accel(X(1)) *h*h
do i = 3,Nt
..............
enddo
V(Nt)= (X(Nt)-X(Nt-1))/h
The full program can be found in the file euler.f90 and is listed below:
!=========================================================
!Program to integrate equations of motion for accelerations
!which are functions of x with the method of Euler,
!Euler-Cromer and Euler-Verlet.
!The user sets initial conditions and the subroutines return
!X(t) and V(t)=dX(t)/dt in arrays T(1..Nt),X(1..Nt),V(1..Nt)
!The user provides number of times Nt and the final
!time Tfi. Initial time is assumed to be t_i=0 and the
!integration step h = Tfi/(Nt-1)
!The user programs a real function accel(x) which gives the
!acceleration dV(t)/dt as function of X.
!NOTE: T(1) = 0 T(Nt) = Tfi
!=========================================================
program diff_eq_euler
implicit none
integer,parameter:: P=110000 ! The size of the arrays
real,dimension(P):: T,X,V ! time t,x(t),v(t)=dx/dt
real :: Xin,Vin,Tfi ! initial conditions
integer :: Nt,i
!The user provides initial conditions X_0,V_0 final time t_f
!and Nt:
print *,’Enter X_0,V_0,t_f,Nt (t_i=0):’
read(5,*)Xin,Vin,Tfi,Nt
!This check is necessary in order to avoid memory
!access violations:
if(Nt .ge. P )then
print *,’Nt must be strictly less than P. Nt,P= ’,Nt,P
stop
endif
!Xin= X(1), Vin=V(1), T(1)=0 and the routine gives evolution in
!T(2..Nt), X(2..Nt), V(2..Nt) which we print in a file
call euler(Xin,Vin,Tfi,Nt,T,X,V)
open(unit=20,file="euler.dat")
do i=1,Nt
!Each line in data file has time, position, velocity:
write(20,*) T(i),X(i),V(i)
enddo
close(20) !we close the unit to be reused below
!------------------------------------
!We repeat everything for each method
call euler_cromer(Xin,Vin,Tfi,Nt,T,X,V)
open(unit=20,file="euler_cromer.dat")
do i=1,Nt
write(20,*) T(i),X(i),V(i)
enddo
close(20)
!------------------------------------
call euler_verlet(Xin,Vin,Tfi,Nt,T,X,V)
open(unit=20,file="euler_verlet.dat")
do i=1,Nt
write(20,*) T(i),X(i),V(i)
enddo
close(20)
!------------------------------------
end program diff_eq_euler
!=========================================================
!Function which returns the value of acceleration at
!position x used in the integration subroutines
!euler, euler_cromer and euler_verlet
!=========================================================
real function accel(x)
implicit none
real x
accel = -10.0*sin(x)
end function accel
!=========================================================
!Driver routine for integrating equations of motion
!using the Euler method
!Input:
!Xin=X(1), Vin=V(1) -- initial condition at t=0,
!Tfi the final time and Nt the number of times
!Output:
!The arrays T(1..Nt), X(1..Nt), V(1..Nt) which
!gives x(t_k)=X(k), dx/dt(t_k)=V(k), t_k=T(k) k=1..Nt
!where for k=1 we have the initial condition.
!=========================================================
subroutine euler(Xin,Vin,Tfi,Nt,T,X,V)
implicit none
integer :: Nt
real,dimension(Nt) :: T,X,V !time t,x(t),v(t)=dx/dt
real :: Xin,Vin,Tfi
integer :: i
real :: h,accel !**declare the function accel**
!Initial conditions set here:
T(1) = 0.0
X(1) = Xin
V(1) = Vin
!h is the time step Dt
h = Tfi/(Nt-1)
do i = 2,Nt
T(i) = T(i-1)+h ! time advances by Dt=h
X(i) = X(i-1)+V(i-1)*h ! advancement of position
V(i) = V(i-1)+accel(X(i-1))*h !and velocity.
enddo
end subroutine euler
!=========================================================
!Driver routine for integrating equations of motion
!using the Euler-Cromer method
!Input:
!Xin=X(1), Vin=V(1) -- initial condition at t=0,
!Tfi the final time and Nt the number of times
!Output:
!The arrays T(1..Nt), X(1..Nt), V(1..Nt) which
!gives x(t_i)=X(i), dx/dt(t_i)=V(i), t_i=T(i) i=1..Nt
!where for i=1 we have the initial condition.
!=========================================================
subroutine euler_cromer(Xin,Vin,Tfi,Nt,T,X,V)
implicit none
integer :: Nt
real,dimension(Nt):: T,X,V !time t,x(t),v(t)=dx/dt
real :: Xin,Vin,Tfi
integer :: i
real :: h,accel
T(1) = 0.0
X(1) = Xin
V(1) = Vin
h = Tfi/(Nt-1)
do i = 2,Nt
T(i) = T(i-1)+h
V(i) = V(i-1)+accel(X(i-1))*h
!here is the difference compared to Euler
X(i) = X(i-1)+V(i)*h
enddo
end subroutine euler_cromer
!=========================================================
!Driver routine for integrating equations of motion
!using the Euler - Verlet method
!Input:
!Xin=X(1), Vin=V(1) -- initial condition at t=0,
!Tfi the final time and Nt the number of times
!Output:
!The arrays T(1..Nt), X(1..Nt), V(1..Nt) which
!gives x(t_i)=X(i), dx/dt(t_i)=V(i), t_i=T(i) i=1..Nt
!where for i=1 we have the initial condition.
!=========================================================
subroutine euler_verlet(Xin,Vin,Tfi,Nt,T,X,V)
implicit none
integer :: Nt
real,dimension(Nt):: T,X,V !time t,x(t),v(t)=dx/dt
real :: Xin,Vin,Tfi
integer :: i
real :: h,h2,X0,o2h
real :: accel
!Initial conditions set here:
T(1) = 0.0
X(1) = Xin
V(1) = Vin
h = Tfi/(Nt-1) ! time step
h2 = h*h ! time step squared
o2h = 0.5/h ! h/2
!We have to initialize one more step: X0 corresponds to ’X(0)’
X0 = X(1) - V(1) * h + accel(X(1)) *h2/2.0
T(2) = h
X(2) = 2.0*X(1) - X0 + accel(X(1)) *h2
!Now i starts from 3:
do i = 3,Nt
T(i) = T(i-1)+h
X(i) = 2.0*X(i-1) - X(i-2) + accel(X(i-1))*h2
V(i-1) = o2h * (X(i)-X(i-2))
enddo
!Notice that we have one more step for the velocity:
V(Nt)= (X(Nt)-X(Nt-1))/h
end subroutine euler_verlet
Compiling the running the program can be done with the commands:
> gfortran euler.f90 -o euler
> ./euler
Enter X_0,V_0,t_f,Nt (t_i=0):
0.2 0.0 6.0 1000
> ls euler*.dat
euler_cromer.dat euler.dat euler_verlet.dat
> head -n 5 euler.dat
0.000000 0.2000000 0.000000
6.0060062E-03 0.2000000 -1.1932093E-02
1.2012012E-02 0.1999283 -2.3864185E-02
1.8018018E-02 0.1997850 -3.5792060E-02
2.4024025E-02 0.1995700 -4.7711499E-02
The last command shows the first 5 lines of the file euler.dat. We see the data
for the time, the position and the velocity stored in 3 columns. We can graph the
results using gnuplot:
gnuplot> plot "euler.dat" using 1:2 with lines
gnuplot> plot "euler.dat" using 1:3 with lines
These commands result in plotting the positions and the velocities as a function
of time respectively. We can add the results of all methods to the last plot with
the commands:
gnuplot> replot "euler_cromer.dat" using 1:3 with lines
gnuplot> replot "euler_verlet.dat" using 1:3 with lines
The results can be seen in figures 4.2–4.7. Euler’s method is unstable unless we
take a quite small time step. The Euler–Cromer method behaves impressively
better. The results converge and remain constant for Nt . The
Euler–Verlet method converges much faster, but roundoff errors kick in soon. This
is more obvious in figure 4.7 where the initial angular position is large. For small
angles we can compare with the solution one obtains for the harmonic pendulum
(
. The
Euler–Verlet method converges much faster, but roundoff errors kick in soon. This
is more obvious in figure 4.7 where the initial angular position is large. For small
angles we can compare with the solution one obtains for the harmonic pendulum
( ):
):
In figures 4.2–4.4 we observe that the results agree with the above formulas for the
values of  where the methods converge. This way we can check our program
for bugs. The plot of the functions above can be done with the following gnuplot
commands :
where the methods converge. This way we can check our program
for bugs. The plot of the functions above can be done with the following gnuplot
commands :
gnuplot> set dummy t
gnuplot> omega2 = 10
gnuplot> X0 = 0.2
gnuplot> V0 = 0.0
gnuplot> omega = sqrt(omega2)
gnuplot> x(t) = X0 * cos(omega * t) +(V0/omega)*sin(omega*t)
gnuplot> v(t) = V0 * cos(omega * t) -(omega*X0)*sin(omega*t)
gnuplot> plot x(t), v(t)
The results should not be compared only graphically since subtle differences can
remain unnoticed. It is more desirable to plot the differences of the theoretical
values from the numerically computed ones which can be done using the
commands:
gnuplot> plot "euler.dat" using 1:($2-x($1)) with lines
gnuplot> plot "euler.dat" using 1:($3-v($1)) with lines
The command using 1:($2-x($1)) puts the values found in the
first column on the  axis and the value found in the second column
minus the value of the function x(t) for
axis and the value found in the second column
minus the value of the function x(t) for  equal to the value found in
the first column on the
equal to the value found in
the first column on the  axis. This way, we can make the plots shown
in
figures 4.11-4.14.
axis. This way, we can make the plots shown
in
figures 4.11-4.14.
4.3 Runge–Kutta Methods
Euler’s method is a one step finite difference method of first order. First
order means that the total error introduced by the discretization of the
integration interval ![[ti,tf]](main_latex1610x.png) by
by  discrete times is of order
discrete times is of order  , where
, where
 is the time step of the integration. In this section we will
discuss a generalization of this approach where the total error will be of higher
order in
is the time step of the integration. In this section we will
discuss a generalization of this approach where the total error will be of higher
order in  . This is the class of Runge-Kutta methods which are one step
algorithms where the total discretization error is of order
. This is the class of Runge-Kutta methods which are one step
algorithms where the total discretization error is of order  . The
local error introduced at each step is of order
. The
local error introduced at each step is of order  leading after
leading after
 steps to a maximum error of order
steps to a maximum error of order
 | (4.15) |
In such a case we say that we have a Runge-Kutta method of  order.
The price one has to pay for the increased accuracy is the evaluation of
the derivatives of the functions in more than one points in the interval
order.
The price one has to pay for the increased accuracy is the evaluation of
the derivatives of the functions in more than one points in the interval
 .
.
Let’s consider for simplicity the problem with only one unknown function
 which evolves in time according to the differential equation:
which evolves in time according to the differential equation:
 | (4.16) |
Consider the first order method first. The most naive approach would be to
take the derivative to be given by the finite difference
 | (4.17) |
By Taylor expanding, we see that the error at each step is  , therefore the
error after integrating from
, therefore the
error after integrating from  is
is  . Indeed,
. Indeed,
 | (4.18) |
The geometry of the step is shown in figure 4.8. We start from point 1 and by
linearly extrapolating in the direction of the derivative  we
determine the point
we
determine the point  .
.
We can improve the method above by introducing an intermediate
point 2. This process is depicted in figure 4.9. We take the point 2 in the
middle of the interval  by making a linear extrapolation from
by making a linear extrapolation from
 in the direction of the derivative
in the direction of the derivative  . Then we use the
slope at point 2 as an estimator of the derivative within this interval, i.e.
. Then we use the
slope at point 2 as an estimator of the derivative within this interval, i.e.
 . We use
. We use  to linearly
extrapolate from
to linearly
extrapolate from  to
to  . Summarizing, we have that
. Summarizing, we have that
For the procedure described above we have to evaluate  twice at each step,
thereby doubling the computational effort. The error at each step (4.19) becomes
twice at each step,
thereby doubling the computational effort. The error at each step (4.19) becomes
 , however, giving a total error of
, however, giving a total error of  . So for given
computational time, (4.19) is superior to (4.17) .
. So for given
computational time, (4.19) is superior to (4.17) .
We can further improve the accuracy gain by using the Runge–Kutta method of
4th order. In this case we have 4 evaluations of the derivative  per step, but the
total error becomes now
per step, but the
total error becomes now  and the method is superior to that of (4.19)
.
The process followed is explained geometrically in figure 4.10. We use 3
intermediate points for evolving the solution from
and the method is superior to that of (4.19)
.
The process followed is explained geometrically in figure 4.10. We use 3
intermediate points for evolving the solution from  to
to  . Point 2 is
determined by linearly extrapolating from
. Point 2 is
determined by linearly extrapolating from  to the midpoint of the
interval
to the midpoint of the
interval  by using the direction given by the derivative
by using the direction given by the derivative
 , i.e.
, i.e.  . We calculate the derivative
. We calculate the derivative
 at the point 2 and we use it in order to determine
point 3, also located at the midpoint of the interval
at the point 2 and we use it in order to determine
point 3, also located at the midpoint of the interval  . Then we calculate
the derivative
. Then we calculate
the derivative  at the point 3 and we use
it to linearly extrapolate to the end of the interval
at the point 3 and we use
it to linearly extrapolate to the end of the interval  , thereby
obtaining point 4, i.e.
, thereby
obtaining point 4, i.e.  . Then we calculate the derivative
. Then we calculate the derivative
 at the point 4, and we use all four derivative
at the point 4, and we use all four derivative  and
and  as estimators of the derivative of the function in the interval
as estimators of the derivative of the function in the interval
 . If each derivative contributes with a particular weight in this
estimate, the discretization error can become
. If each derivative contributes with a particular weight in this
estimate, the discretization error can become  . Such a choice is
. Such a choice is

We note that the second term of the last equation takes an average of the four
derivatives with weights  ,
,  ,
,  and
and  respectively. A generic small
change in these values will increase the discretization error to worse than
respectively. A generic small
change in these values will increase the discretization error to worse than
 .
.
We remind to the reader the fact that by decreasing  the discretization
errors decrease, but that roundoff errors will start showing up for small enough
the discretization
errors decrease, but that roundoff errors will start showing up for small enough
 . Therefore, a careful determination of
. Therefore, a careful determination of  that minimizes the total error
should be made by studying the dependence of the results as a function of
that minimizes the total error
should be made by studying the dependence of the results as a function of
 .
.
4.3.1 A Program for the 4th Order Runge–Kutta
Consider the problem of the motion of a particle in one dimension. For
this, we have to integrate a system of two differential equations (4.5)
for two unknown functions of time  and
and  so
that
so
that
 | (4.21) |
In this case, equations (4.20) generalize to:

Programming this algorithm is quite simple. The main program is an interface
between the user and the driver routine of the integration. The user enters the
initial and final times  Ti and
Ti and  Tf and the number of discrete time
points Nt. The initial conditions are
Tf and the number of discrete time
points Nt. The initial conditions are  X10,
X10,  X20. The main data
structure consists of three real arrays T(P), X1(P), X2(P) which store the times
X20. The main data
structure consists of three real arrays T(P), X1(P), X2(P) which store the times
 and the corresponding values of the functions
and the corresponding values of the functions  and
and  ,
,  . The main program calls the driver routine
RK(T,X1,X2,Ti,Tf,X10,X20,Nt) which “drives” the heart of the program, the
subroutine RKSTEP(t,x1,x2,dt) which performs one integration step using
equations (4.22) . RKSTEP evolves the functions x1, x2 at time t by one step
. The main program calls the driver routine
RK(T,X1,X2,Ti,Tf,X10,X20,Nt) which “drives” the heart of the program, the
subroutine RKSTEP(t,x1,x2,dt) which performs one integration step using
equations (4.22) . RKSTEP evolves the functions x1, x2 at time t by one step  dt. The routine RK stores the calculated values in the arrays T, X1 and X2 at each
step. When RK returns the control to the main program, all the results
are stored in T, X1 and X2, which are subsequently printed in the file
rk.dat. The full program is listed below and can be found in the file
rk.f90:
dt. The routine RK stores the calculated values in the arrays T, X1 and X2 at each
step. When RK returns the control to the main program, all the results
are stored in T, X1 and X2, which are subsequently printed in the file
rk.dat. The full program is listed below and can be found in the file
rk.f90:
!========================================================
!Program to solve a 2 ODE system using Runge-Kutta Method
!User must supply derivatives
!dx1/dt=f1(t,x1,x2) dx2/dt=f2(t,x1,x2)
!as real functions
!Output is written in file rk.dat
!========================================================
program rk_solve
implicit none
integer, parameter :: P=110000
real,dimension(P) :: T,X1,X2
real :: Ti,Tf,X10,X20
integer :: Nt
integer :: i
!Input:
print *,’Runge-Kutta Method for 2-ODEs Integration’
print *,’Enter Nt,Ti,TF,X10,X20:’
read *, Nt,Ti,Tf,X10,X20
print *,’Nt = ’,Nt
print *,’Time: Initial Ti =’,Ti,’ Final Tf=’,Tf
print *,’ X1(Ti)=’,X10,’ X2(Ti)=’,X20
if(Nt.gt.P) stop ’Nt>P’
!The Calculation:
call RK(T,X1,X2,Ti,Tf,X10,X20,Nt)
!Output:
open(unit=11,file=’rk.dat’)
do i=1,Nt
write(11,*)T(i),X1(i),X2(i)
enddo
close(11)
end program rk_solve
!========================================================
!The functions f1,f2(t,x1,x2) provided by the user
!========================================================
real function f1(t,x1,x2)
implicit none
real :: t,x1,x2
f1=x2 !dx1/dt= v = x2
end function f1
!--------------------------------------------------------
real function f2(t,x1,x2)
implicit none
real :: t,x1,x2
f2=-10.0D0*x1 !harmonic oscillator
end function f2
!========================================================
!RK(T,X1,X2,Ti,Tf,X10,X20,Nt) is the driver
!for the Runge-Kutta integration routine RKSTEP
!Input: Initial and final times Ti,Tf
! Initial values at t=Ti X10,X20
! Number of steps of integration: Nt-1
! Size of arrays T,X1,X2
!Output: real arrays T(Nt),X1(Nt),X2(Nt) where
!T(1) = Ti X1(1) = X10 X2(1) = X20
! X1(k) = X1(at t=T(k)) X2(k) = X2(at t=T(k))
!T(Nt)=TF
!========================================================
subroutine RK(T,X1,X2,Ti,Tf,X10,X20,Nt)
implicit none
integer :: Nt
real,dimension(Nt):: T,X1,X2
real :: Ti,Tf,X10,X20
real :: dt
real :: TS,X1S,X2S !values of time and X1,X2 at given step
integer :: i
!Initialize variables:
dt = (Tf-Ti)/(Nt-1)
T (1) = Ti
X1(1) = X10
X2(1) = X20
TS = Ti
X1S = X10
X2S = X20
!Make RK steps: The arguments of RKSTEP
!are replaced with the new ones!
do i=2,Nt
call RKSTEP(TS,X1S,X2S,dt)
T (i) = TS
X1(i) = X1S
X2(i) = X2S
enddo
end subroutine RK
!========================================================
!Subroutine RKSTEP(t,x1,x2,dt)
!Runge-Kutta Integration routine of ODE
!dx1/dt=f1(t,x1,x2) dx2/dt=f2(t,x1,x2)
!User must supply derivative functions:
!real function f1(t,x1,x2)
!real function f2(t,x1,x2)
!Given initial point (t,x1,x2) the routine advances it
!by time dt.
!Input : Inital time t and function values x1,x2
!Output: Final time t+dt and function values x1,x2
!Careful!: values of t,x1,x2 are overwritten...
!========================================================
subroutine RKSTEP(t,x1,x2,dt)
implicit none
real :: t,x1,x2,dt
real :: f1,f2
real :: k11,k12,k13,k14,k21,k22,k23,k24
real :: h,h2,h6
h =dt !h =dt, integration step
h2 =0.5D0*h !h2=h/2
h6 =h/6.0 !h6=h/6
k11=f1(t,x1,x2)
k21=f2(t,x1,x2)
k12=f1(t+h2,x1+h2*k11,x2+h2*k21)
k22=f2(t+h2,x1+h2*k11,x2+h2*k21)
k13=f1(t+h2,x1+h2*k12,x2+h2*k22)
k23=f2(t+h2,x1+h2*k12,x2+h2*k22)
k14=f1(t+h ,x1+h *k13,x2+h *k23)
k24=f2(t+h ,x1+h *k13,x2+h *k23)
t =t+h
x1 =x1+h6*(k11+2.0D0*(k12+k13)+k14)
x2 =x2+h6*(k21+2.0D0*(k22+k23)+k24)
end subroutine RKSTEP
4.4 Comparison of the Methods
In this section we will check our programs for correctness and accuracy w.r.t.
discretization and roundoff errors. The simplest test is to check the results against
a known analytic solution of a simple model. This will be done for the simple
harmonic oscillator. Our programs will need small changes which are summarized
below. First, we will need to use higher accuracy variables and we will change
all variables of type REAL to REAL(8). For this we need to change the
corresponding declarations in the beginning of each (sub)program. For each
numerical constant in the program we need to put an explicit exponent
with the letter D instead of an E. For example 0.5  0.5D0, 1.2E-3
0.5D0, 1.2E-3
 1.2D-3 etc. Then we need to alter the functions that compute the
acceleration of the particle to give
1.2D-3 etc. Then we need to alter the functions that compute the
acceleration of the particle to give  . We will take
. We will take  (
( ). Therefore the relevant part of the program in euler.f90
becomes
). Therefore the relevant part of the program in euler.f90
becomes
real(8) function accel(x)
implicit none
real(8) :: x
accel = -10.0D0*x
end function accel
and that of the program in rk.f90 becomes
real(8) function f2(t,x1,x2)
implicit none
real(8) :: t,x1,x2
f2=-10.0D0*x1
end function f2
The programs are run for a given time interval  to
to  with the
initial conditions
with the
initial conditions  ,
,  . The time step
. The time step  is varied by
varying the number of steps Nt-1. The computed numerical solution is
compared to the well known solution for the simple harmonic oscillator
is varied by
varying the number of steps Nt-1. The computed numerical solution is
compared to the well known solution for the simple harmonic oscillator
We study the deviation  and
and  as a
function of the time step
as a
function of the time step  . The results are shown in figures 4.11–4.14. We
note that for the Euler method and the Euler–Cromer method, the errors
are of order
. The results are shown in figures 4.11–4.14. We
note that for the Euler method and the Euler–Cromer method, the errors
are of order  as expected. However, the latter has smaller errors
compared to the first one. For the Euler–Verlet method, the error turns out
to be of order
as expected. However, the latter has smaller errors
compared to the first one. For the Euler–Verlet method, the error turns out
to be of order  whereas for the 4th order Runge–Kutta is of
order
whereas for the 4th order Runge–Kutta is of
order
 .
.
Another way for checking the numerical results is by looking at a conserved
quantity, like the energy, momentum or angular momentum, and study its
deviation from its original value. In our case we study the mechanical
energy
 | (4.24) |
which is computed at each step. The deviation  is shown in figures
4.15–4.18.
is shown in figures
4.15–4.18.
4.5 The Forced Damped Oscillator
In this section we will study a simple harmonic oscillator subject to a damping
force proportional to its velocity and an external periodic driving force,
which for simplicity will be taken to have a sinusoidal dependence in
time,
 | (4.25) |
where  and
and  is the angular frequency of the driving
force.
is the angular frequency of the driving
force.
Consider initially the system without the influence of the driving
force, i.e. with  . The real solutions of the differential
equation
which are finite for
. The real solutions of the differential
equation
which are finite for  are given by
are given by
 | (4.26) |
 | (4.27) |
In the last case, the solution oscillates with an amplitude decreasing exponentially
with time.
In the  case, the general solution is obtained from the sum of a special
solution
case, the general solution is obtained from the sum of a special
solution  and the solution of the homogeneous equation
and the solution of the homogeneous equation  . A special
solution can be obtained from the ansatz
. A special
solution can be obtained from the ansatz  ,
which when substituted in (4.25) and solved for
,
which when substituted in (4.25) and solved for  and
and  we find
that
we find
that
![a0 [(ω20 − ω2 )cosωt + γ ωsin ωt]
xs(t) = ---------2----2-2----2-2-------,
(ω 0 − ω ) + ω γ](main_latex1734x.png) | (4.29) |
and
 | (4.30) |
The solution  decreases exponentially with time and eventually only
decreases exponentially with time and eventually only
 remains. The only case where this is not true, is when we have
resonance without damping for
remains. The only case where this is not true, is when we have
resonance without damping for  ,
,  . In that case the solution
is
. In that case the solution
is
 | (4.31) |
The first two terms are the same as that of the simple harmonic oscillator. The
last one increases the amplitude linearly with time, which is a result of the influx
of energy from the external force to the oscillator.
Our program will be a simple modification of the program in rk.f90. The
main routines RK(T,X1,X2,T0,TF,X10,X20,Nt) and RKSTEP(t,x1,x2,dt) remain
as they are. We only change the user interface. The basic parameters  ,
,  ,
,
 ,
,  are entered interactively by the user from the standard input stdin.
These parameters should be accessible also by the function f2(t,x1,x2), and one
way to be able to do this, is to store them in variables which are placed in a
common block. Such variables are accessible to all subprograms that declare a
common block with the same name using a COMMON declaration. Such a
declaration is shown in the following lines
are entered interactively by the user from the standard input stdin.
These parameters should be accessible also by the function f2(t,x1,x2), and one
way to be able to do this, is to store them in variables which are placed in a
common block. Such variables are accessible to all subprograms that declare a
common block with the same name using a COMMON declaration. Such a
declaration is shown in the following lines
real(8) :: omega_0,omega,gamma,a_0,omega_02,omega2
common /params/omega_0,omega,gamma,a_0,omega_02,omega2
which when written in a (sub)program, the (sub)program gains access to the
“memory position” params where the values of the variables are stored. Another
point that needs our attention is the function f2(t,x1,x2) which now takes the
velocity  x2 in its arguments:
x2 in its arguments:
real(8) function f2(t,x1,x2)
implicit none
real(8) omega_0,omega,gamma,a_0,omega_02,omega2
common /params/omega_0,omega,gamma,a_0,omega_02,omega2
real(8) t,x1,x2,a
a = a_0*cos(omega*t)
f2=-omega_02*x1-gamma*x2+a
end function f2
The main program found in the file dlo.f90 is listed below. The subroutines RK,
RKSTEP are the same as in rk.f90 and should also be included in the same
file.
!========================================================
!Program to solve Damped Linear Oscillator
!using 4th order Runge-Kutta Method
!Output is written in file dlo.dat
!========================================================
program dlo_solve
implicit none
integer, parameter :: P=110000
real(8),dimension(P):: T,X1,X2
real(8) :: Ti,Tf,X10,X20
real(8) :: Energy
real(8) :: omega_0,omega,gamma,a_0,omega_02,omega2
common /params/omega_0,omega,gamma,a_0,omega_02,omega2
integer :: Nt, i
!Input:
print *,’Runge-Kutta Method for DLO Integration’
print *,’Enter omega_0, omega, gamma, a_0:’
read *, omega_0,omega,gamma,a_0
omega_02 = omega_0*omega_0
omega2 = omega *omega
print *, ’omega_0= ’,omega_0,’ omega= ’, omega
print *, ’gamma= ’,gamma, ’ a_0= ’,a_0
print *,’Enter Nt,Ti,TF,X10,X20:’
read *, Nt,Ti,Tf,X10,X20
print *,’Nt = ’,Nt
print *,’Time: Initial Ti =’,Ti,’ Final Tf=’,Tf
print *,’ X1(Ti)=’,X10,’ X2(Ti)=’,X20
if(Nt.gt.P) stop ’Nt>P’
!The Calculation:
call RK(T,X1,X2,Ti,Tf,X10,X20,Nt)
!Output:
open(unit=11,file=’dlo.dat’)
write(11,*)’# Damped Linear Oscillator - dlo’
write(11,*)’# omega_0= ’,omega_0,’ omega= ’, omega,&
’ gamma= ’,gamma,’ a_0= ’,a_0
do i=1,Nt
Energy = 0.5D0*X2(i)*X2(i)+0.5D0*omega_02*X1(i)*X1(i)
write(11,*)T(i),X1(i),X2(i),Energy
enddo
close(11)
end program dlo_solve
!========================================================
!The functions f1,f2(t,x1,x2) provided by the user
!========================================================
real(8) function f1(t,x1,x2)
implicit none
real(8) t,x1,x2
f1=x2 !dx1/dt= v = x2
end function f1
!--------------------------------------------------------
real(8) function f2(t,x1,x2)
implicit none
real(8) omega_0,omega,gamma,a_0,omega_02,omega2
common /params/omega_0,omega,gamma,a_0,omega_02,omega2
real(8) t,x1,x2,a
a = a_0*cos(omega*t)
f2=-omega_02*x1-gamma*x2+a
end function f2
The results are shown in figures 4.19–4.22. Figure 4.19 shows the transition
from a damped motion for  to an oscillating motion with damping
amplitude for
to an oscillating motion with damping
amplitude for  . The exponential decrease of the amplitude is shown in
figure 4.21, whereas the dependence of the period
. The exponential decrease of the amplitude is shown in
figure 4.21, whereas the dependence of the period  from the damping coefficient
from the damping coefficient
 is shown in figure 4.22. Motivated by equation (4.28) , written in the
form
is shown in figure 4.22. Motivated by equation (4.28) , written in the
form
 | (4.32) |
we construct the plot in figure 4.22. The right hand side of the equation is put on
the horizontal axis, whereas the left hand side on the vertical. Equation (4.32)
predicts that both quantities are equal and all measurements should lie on a
particular line, the diagonal  . The period
. The period  can be estimated from the
time between two consecutive extrema of
can be estimated from the
time between two consecutive extrema of  or two consecutive zeros of the
velocity
or two consecutive zeros of the
velocity  (see figure 4.19).
(see figure 4.19).
Finally it is important to study the trajectory of the system in phase space. This can
be seen
in figure 4.20. A point in this space is a state of the system and a trajectory
describes the evolution of the system’s states in time. We see that all such
trajectories end up as  to the point
to the point  , independently of the
initial conditions. Such a point is an example of a system’s attractor.
, independently of the
initial conditions. Such a point is an example of a system’s attractor.
Next, we add the external force and study the response of the system to it.
The system exhibits a transient behavior that depends on the initial conditions.
For large enough times it approaches a steady state that does not depend
on (almost all of) the initial conditions. This can be seen in figure 4.23.
This is easily understood for our system by looking at equations (4.26) –
(4.28) . We see that the steady state  becomes dominant when
the exponentials have damped away.
becomes dominant when
the exponentials have damped away.  can be written in the form
can be written in the form
These equations are verified in figure 4.24 where we study the dependence of the
amplitude  on the angular frequency of the driving force. Finally we study
the trajectory of the system in phase space. As we can see in figure 4.20, this time
the attractor is an ellipse, which is a one dimensional curve instead of a zero
dimensional point. For large enough times, all trajectories approach their
attractor asymptotically.
on the angular frequency of the driving force. Finally we study
the trajectory of the system in phase space. As we can see in figure 4.20, this time
the attractor is an ellipse, which is a one dimensional curve instead of a zero
dimensional point. For large enough times, all trajectories approach their
attractor asymptotically.
4.6 The Forced Damped Pendulum
In this section we will study a non-linear dynamical system which exhibits
interesting chaotic behavior. This is a simple model which, despite its
deterministic nature, the prediction of its future behavior becomes intractable
after a short period of time. Consider a simple pendulum in a constant
gravitational field whose motion is damped by a force proportional to its
velocity and it is under the influence of a vertical, harmonic external driving
force:
 | (4.34) |
In the equation above,  is the angle of the pendulum with the vertical axis,
is the angle of the pendulum with the vertical axis,  is the damping coefficient,
is the damping coefficient,  is the pendulum’s natural angular
frequency,
is the pendulum’s natural angular
frequency,  is the angular frequency of the driving force and
is the angular frequency of the driving force and  is
the amplitude of the external angular acceleration caused by the driving
force.
is
the amplitude of the external angular acceleration caused by the driving
force.
In the absence of the driving force, the damping coefficient drives the system
to the point  , which is an attractor for the system. This continues
to happen for small enough
, which is an attractor for the system. This continues
to happen for small enough  , but for
, but for  the behavior of the system
becomes more complicated.
the behavior of the system
becomes more complicated.
The program that integrates the equations of motion of the system can be
obtained by making trivial changes to the program in the file dlo.f90.
This changes are listed in detail below, but we note that X1  , X2
, X2
 , a_0
, a_0  . The final program can be found in the file fdp.f90. It
is listed below, with the understanding that the commands in between
the dots are the same as in the programs found in the files dlo.f90,
rk.f90.
. The final program can be found in the file fdp.f90. It
is listed below, with the understanding that the commands in between
the dots are the same as in the programs found in the files dlo.f90,
rk.f90.
!========================================================
!Program to solve Forced Damped Pendulum
!using 4th order Runge-Kutta Method
!Output is written in file fdp.dat
!========================================================
program dlo_solve
implicit none
integer, parameter :: P=1010000
................................
Energy = 0.5D0*X2(i)*X2(i)+omega_02*(1.0D0-cos(X1(i)))
................................
end program dlo_solve
!--------------------------------------------------------
real(8) function f2(t,x1,x2)
implicit none
real(8) omega_0,omega,gamma,a_0,omega_02,omega2
common /params/omega_0,omega,gamma,a_0,omega_02,omega2
real(8) t,x1,x2
f2=-(omega_02+2.0D0*a_0*cos(omega*t))*sin(x1)-gamma*x2
end function f2
!========================================================
subroutine RKSTEP(t,x1,x2,dt)
implicit none
................................
real(8),parameter :: pi =3.14159265358979324D0
real(8),parameter :: pi2=6.28318530717958648D0
................................
x1 =x1+h6*(k11+2.0D0*(k12+k13)+k14)
x2 =x2+h6*(k21+2.0D0*(k22+k23)+k24)
if( x1 .gt. pi) x1 = x1 - pi2
if( x1 .lt. -pi) x1 = x1 + pi2
end subroutine RKSTEP
The final lines in the program are added so that the angle is kept within the
interval ![[− π,π]](main_latex1801x.png) .
.
In order to study the system’s properties we will set  ,
,  , and
, and
 unless we explicitly state otherwise. The natural period of the pendulum
is
unless we explicitly state otherwise. The natural period of the pendulum
is  whereas that of the driving force is
whereas that of the driving force is
 . For
. For  , with
, with  , the
point
, the
point  is an attractor, which means that the pendulum eventually
stops at its stable equilibrium point. For
is an attractor, which means that the pendulum eventually
stops at its stable equilibrium point. For  the attractor is a
closed curve, which means that the pendulum at its steady state oscillates
indefinitely without circling through its unstable equilibrium point at
the attractor is a
closed curve, which means that the pendulum at its steady state oscillates
indefinitely without circling through its unstable equilibrium point at  .
The period of motion is found to be twice that of the driving force. For
.
The period of motion is found to be twice that of the driving force. For
 the attractor is an open curve, because at its steady state the
pendulum crosses the
the attractor is an open curve, because at its steady state the
pendulum crosses the  point. The period of the motion becomes
equal to that of the driving force. For
point. The period of the motion becomes
equal to that of the driving force. For  we have period
doubling for critical values of
we have period
doubling for critical values of  , but the trajectory is still periodic. For
even larger values of
, but the trajectory is still periodic. For
even larger values of  the system enters into a chaotic regime where
the trajectories are non periodic. For
the system enters into a chaotic regime where
the trajectories are non periodic. For  we find the system in a
periodic steady state again, whereas for
we find the system in a
periodic steady state again, whereas for  –
–  we have period
doubling. For
we have period
doubling. For  we enter into a chaotic regime again etc. These
results can be seen in figures 4.27–4.29. The reader should construct the
bifurcation diagram of the system by solving problem 20 of this chapter.
we enter into a chaotic regime again etc. These
results can be seen in figures 4.27–4.29. The reader should construct the
bifurcation diagram of the system by solving problem 20 of this chapter.
We can also use the so called Poincaré diagrams in order to study the chaotic
behavior of a system. These are obtained by placing a point in phase
space when the time is an integer multiple of the period of the driving
force. Then, if for example the period of the motion is equal to that of
the period of the driving force, the Poincaré diagram consists of only
one point. If the period of the motion is an  –multiple of the period of
the driving force then the Poincaré diagram consists of only
–multiple of the period of
the driving force then the Poincaré diagram consists of only  points.
Therefore, in the period doubling regime, the points of the Poincaré diagram
double at each period doubling point. In the chaotic regime, the Poincaré
diagram consists of an infinite number of points which belong to sets that
have interesting fractal structure. One way to construct the Poincaré
diagram numerically, is to process the data of the output file fdp.dat using
awk :
points.
Therefore, in the period doubling regime, the points of the Poincaré diagram
double at each period doubling point. In the chaotic regime, the Poincaré
diagram consists of an infinite number of points which belong to sets that
have interesting fractal structure. One way to construct the Poincaré
diagram numerically, is to process the data of the output file fdp.dat using
awk :
awk -v o=$omega -v nt=$Nt -v tf=$TF \
’BEGIN{T=6.283185307179/o;dt=tf/nt;} $1%T<dt{print $2,$3}’\
fdp.dat
where $omega, $Nt, $TF are the values of the angular frequency  ,
the number of points of time and the final time
,
the number of points of time and the final time  . We calculate
the period T and the time step dt in the program. Then we print
those lines of the file where the time is an integer multiple of the
period .
This is accomplished by the modulo operation $1 % T. The value of the
expression $1 % T < dt is true when the remainder of the division of the first
column ($1) of the file fdp.dat with the period T is smaller than dt. The results
in the chaotic regime are displayed in figure 4.30.
. We calculate
the period T and the time step dt in the program. Then we print
those lines of the file where the time is an integer multiple of the
period .
This is accomplished by the modulo operation $1 % T. The value of the
expression $1 % T < dt is true when the remainder of the division of the first
column ($1) of the file fdp.dat with the period T is smaller than dt. The results
in the chaotic regime are displayed in figure 4.30.
We close this section by discussing another concept that helps us in
the analysis of the dynamical properties of the pendulum. This is the
concept of the basin of attraction which is the set of initial conditions in
phase space that lead the system to a specific attractor. Take for example
the case for  in the regime where the pendulum at its steady
state has a circular trajectory with a positive or negative direction. By
taking a large sample of initial conditions and recording the direction of
the resulting motion after the transient behavior, we obtain figure 4.31.
in the regime where the pendulum at its steady
state has a circular trajectory with a positive or negative direction. By
taking a large sample of initial conditions and recording the direction of
the resulting motion after the transient behavior, we obtain figure 4.31.
4.7 Appendix: On the Euler–Verlet Method
Equations (4.11) can be obtained from the Taylor expansion
By adding and subtracting the above equations we obtain which give equations (4.11) From the first equation and equations (4.9) we obtain:
 | (4.37) |
When we perform a numerical integration, we are interested in the total error
accumulated after  integration steps. In this method, these errors must be
studied carefully:
integration steps. In this method, these errors must be
studied carefully:
Therefore the total error is  .
.
We also mention the Velocity Verlet method or the Leapfrog method. In this
case we use the velocity explicitly:
The last step uses the acceleration  which should depend only on the
position
which should depend only on the
position  and not on the velocity.
and not on the velocity.
The Verlet methods are popular in molecular dynamics simulations of many
body systems. One of their advantages is that the constraints of the system of
particles are easily encoded in the algorithm.
4.8 Appendix: 2nd order Runge–Kutta Method
In this appendix we will show how the choice of the intermediate point 2 in
equation (4.17) reduces the error by a power of  . This choice is special, since
by choosing another point (e.g.
. This choice is special, since
by choosing another point (e.g.  ) the result would have not been the
same. Indeed, from the relation
) the result would have not been the
same. Indeed, from the relation
 | (4.40) |
By Taylor expanding around the point  we obtain
we obtain
 | (4.41) |
Therefore
Note that for the vanishing of the  term it is necessary to place the
intermediate point at time
term it is necessary to place the
intermediate point at time  .
.
This is not a unique choice. This can be most easily seen by a different
analysis of the Taylor expansion. Expanding around the point  we obtain
we obtain
where we have set  ,
,  etc. We define and we will determine the conditions so that the terms
etc. We define and we will determine the conditions so that the terms  of the last
equation in the error are identical with those of equation (4.43) . By expanding
of the last
equation in the error are identical with those of equation (4.43) . By expanding
 we obtain Substituting in (4.44) we obtain All we need is to choose The choice
we obtain Substituting in (4.44) we obtain All we need is to choose The choice  ,
,  ,
,  leads to equation (4.19) . Some other
choices in the bibliography are
leads to equation (4.19) . Some other
choices in the bibliography are  and
and  .
.
4.9 Problems
- Prove that the total error in the Euler–Cromer method is of order
 .
.
- Reproduce the results in figures 4.11–4.18
- Improve your programs so that there is no accumulation of roundoff
error in the calculation of time when h is very small for the
methods Euler, Euler-Cromer, Euler-Verlet and Runge-Kutta. Repeat
the analysis of the previous problem.
- Make the appropriate changes in your programs of the Euler,
Euler-Cromer, Euler-Verlet and Runge-Kutta methods so that all
floating variables change from REAL
 REAL(8). Repeat the analysis
of the previous problem.
REAL(8). Repeat the analysis
of the previous problem.
- Compare the results obtained from the Euler, Euler-Cromer, Euler-Verlet,
Runge-Kutta methods for the following systems where the analytic solution
is known:
- Particle falling in a constant gravitational field. Consider the case
 ,
,  ,
,  .
.
- Particle falling in a constant gravitational field moving in a fluid
from which exerts a force
 on the particle. Consider the
case
on the particle. Consider the
case  ,
,  ,
, 
 . Calculate the
limiting velocity of the particle numerically and compare the value
obtained to the theoretical expectation.
. Calculate the
limiting velocity of the particle numerically and compare the value
obtained to the theoretical expectation.
- Repeat for the case of a force of resistance of magnitude
 .
.
- Consider the damped harmonic oscillator
 | (4.48) |
Take  ,
,  and calculate its mechanical energy as a
function of time. Is it monotonic? Why? (show that
and calculate its mechanical energy as a
function of time. Is it monotonic? Why? (show that  ).
Repeat for
).
Repeat for  . When is the system oscillating and when it’s
not? Calculate numerically the critical value of
. When is the system oscillating and when it’s
not? Calculate numerically the critical value of  for which the system
passes from a non oscillating to an oscillating regime. Compare your results
with the theoretical expectations.
for which the system
passes from a non oscillating to an oscillating regime. Compare your results
with the theoretical expectations.
- Reproduce the results of figures 4.19–4.22.
- Reproduce the results of figures 4.23–4.26. Calculate the phase
 numerically and compare with equation (4.33) .
numerically and compare with equation (4.33) .
- Consider a simple model for a swing. Take the damped harmonic oscillator
and a driving force which periodically exerts a momentary push with
angular frequency
 . Define “momentary” to be an impulse given by the
acceleration
. Define “momentary” to be an impulse given by the
acceleration  by an appropriately small time interval
by an appropriately small time interval  . The
acceleration is
. The
acceleration is  for all other times. Calculate the amplitude
for all other times. Calculate the amplitude  for
for
 and
and  .
.
- Consider a “half sine” driving force on a damped harmonic oscillator
 Study the transient behavior of the system for several initial conditions and
calculate its steady state motion for
Study the transient behavior of the system for several initial conditions and
calculate its steady state motion for  and
and  . Calculate
the amplitude
. Calculate
the amplitude  .
.
- Consider the driving force on a damped oscillator given by
 Study the transient behavior of the system for several initial conditions and
calculate its steady state motion for
Study the transient behavior of the system for several initial conditions and
calculate its steady state motion for  and
and  . Calculate
the amplitude
. Calculate
the amplitude  . Compare your results with those of the previous
problem and comment about.
. Compare your results with those of the previous
problem and comment about.
- Write a program that simulates
 identical, independent harmonic
oscillators. Take
identical, independent harmonic
oscillators. Take  and choose random initial conditions for each one
of them. Study their trajectories in phase space and check whether they
cross each other. Comment on your results.
and choose random initial conditions for each one
of them. Study their trajectories in phase space and check whether they
cross each other. Comment on your results.
- Place the
 harmonic oscillators of the previous problem in a
small square in phase space whose center is at the origin of the
axes. Consider the evolution of the system in time. Does the shape
of the rectangle change in time? Does the area change in time?
Explain...
harmonic oscillators of the previous problem in a
small square in phase space whose center is at the origin of the
axes. Consider the evolution of the system in time. Does the shape
of the rectangle change in time? Does the area change in time?
Explain...
- Repeat the previous problem when each oscillator is damped with
 .
Take
.
Take  .
.
- Consider the forced damped oscillator with
 ,
,  ,
,  .
Study the transient behavior of the system in the plots of
.
Study the transient behavior of the system in the plots of  ,
,  for
for
 .
.
- Consider the forced damped pendulum with
 ,
,  ,
,  and study the phase space trajectories for
and study the phase space trajectories for  0.1, 0.19, 0.21, 0.25, 0.5,
0.71, 0.79, 0.85, 1.02, 1.031, 1.033, 1.05, 1.08, 1.1, 1.4, 1.8, 3.1, 3.5, 3.8, 4.2,
4.42, 4.44, 4.445, 4.447, 4.4488. Consider both the transient behavior and
the steady state motion.
0.1, 0.19, 0.21, 0.25, 0.5,
0.71, 0.79, 0.85, 1.02, 1.031, 1.033, 1.05, 1.08, 1.1, 1.4, 1.8, 3.1, 3.5, 3.8, 4.2,
4.42, 4.44, 4.445, 4.447, 4.4488. Consider both the transient behavior and
the steady state motion.
- Reproduce the results in figures 4.30.
- Reproduce the results in figures 4.31.
- Consider the forced damped oscillator with
 After the transient behavior, the motion of the system for
After the transient behavior, the motion of the system for  ,
,
 and
and  is periodic. Measure the period of the
motion with an accuracy of three significant digits and compare it
with the natural period of the pendulum and with the period of the
driving force. Take as initial conditions the following pairs:
is periodic. Measure the period of the
motion with an accuracy of three significant digits and compare it
with the natural period of the pendulum and with the period of the
driving force. Take as initial conditions the following pairs: 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  . Check if the period is independent of the initial
conditions.
. Check if the period is independent of the initial
conditions.
- Consider the forced damped pendulum with
 Study the motion of the pendulum when the amplitude
Study the motion of the pendulum when the amplitude  takes values in
the interval
takes values in
the interval ![[0.2,5.0]](main_latex1956x.png) . Consider specific discrete values of
. Consider specific discrete values of  by splitting
the interval above in subintervals of width equal to
by splitting
the interval above in subintervals of width equal to  .
For each value of
.
For each value of  , record in a file the value of
, record in a file the value of  , the angular
position and the angular velocity of the pendulum when
, the angular
position and the angular velocity of the pendulum when  with
with
 :
:
 The choice of
The choice of  is made so that the transient behavior will be
discarded and study only the steady state of the pendulum. You
may take
is made so that the transient behavior will be
discarded and study only the steady state of the pendulum. You
may take  ,
,  ,
, 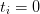 ,
,  , and
split the intervals
, and
split the intervals ![[tk,tk + π]](main_latex1969x.png) to 50 subintervals. Choose
to 50 subintervals. Choose  ,
,
 .
.
- Construct the bifurcation diagram by plotting the points
 .
.
- Repeat by plotting the points
 .
.
- Check whether your results depend on the choice of
 ,
,  .
Repeat your analysis for
.
Repeat your analysis for  ,
,  .
.
- Study the onset of chaos: Take
![A ∈ [1.0000,1.0400]](main_latex1978x.png) with
with
 and
and ![A ∈ [4.4300,4.4500]](main_latex1980x.png) with
with  and
compute with the given accuracy the value
and
compute with the given accuracy the value  where the system
enters into the chaotic behavior regime.
where the system
enters into the chaotic behavior regime.
- The plot the points
 for
for 




 . Put 2000 points for each value of
. Put 2000 points for each value of  and
commend on the strength of the chaotic behavior of the pendulum.
and
commend on the strength of the chaotic behavior of the pendulum.
Chapter 5
Planar Motion
In this chapter we will study the motion of a particle moving on the plane under
the influence of a dynamical field. Special emphasis will be given to the study of
the motion in a central field, like in the problem of planetary motion and
scattering. We also study the motion of two or more interacting particles moving
on the plane, which requires the solution of a larger number of dynamical
equations. These problems can be solved numerically by using Runge–Kutta
integration methods, therefore this chapter extends and applies the numerical
methods studied in the previous chapter.
5.1 Runge–Kutta for Planar Motion
In two dimensions, the initial value problem that we are interested in, is solving
the system of equations (4.6)
The 4th order Runge-Kutta method can be programmed by making small
modifications of the program in the file rk.f90. In order to facilitate the study of
many different dynamical fields, for each field we put the code of the respective
acceleration in a different file. The code which is common for all the forces,
namely the user interface and the implementation of the Runge–Kutta method,
will be put in the file rk2.f90. The program that computes the acceleration will
be put in a file named rk_XXX.f90, where XXX is a string of characters that
identifies the force. For example, the file rk2_hoc.f90 contains the program
computing the acceleration of the simple harmonic oscillator, the file
rk2_g.f90 the acceleration of a constant gravitational field  etc.
etc.
Different force fields will require the use of one or more coupling constants
which need to be accessible to the code in the main program and some
subroutines. For this reason, we will provide two variables k1, k2 in a common
block:
real(8) :: k1,k2
common /couplings/k1,k2
This common block will be accessed by the acceleration functions f3 and f4, the
function energy and the main program where the user will enter the values of k1
and k2. The initial conditions are stored in the variables X10  , X20
, X20
 , V10
, V10  , V20
, V20  , and the values of the functions of
time will be stored in the arrays X1(P)
, and the values of the functions of
time will be stored in the arrays X1(P)  , X2(P)
, X2(P)  , V1(P)
, V1(P)
 , V2(P)
, V2(P)  . The integration is performed by a call to the
subroutine
. The integration is performed by a call to the
subroutine
call RK(T,X1,X2,V1,V2,Ti,Tf,X10,X20,V10,V20,Nt)
The results are written to the file rk2.dat. Each line in this file contains the
time, position, velocity and the total mechanical energy, where the energy is
calculated by the function energy(t,x1,x2,v1,v2):
open(unit=11,file=’rk2.dat’)
do i=1,Nt
write(11,*)T(i),X1(i),X2(i),V1(i),V2(i),&
energy(T(i),X1(i),X2(i),V1(i),V2(i))
enddo
The code for the function energy, which is different for each force field, is
written in the same file with the acceleration. The code for the subroutine
RKSTEP(t,x1,x2,x3,x4,dt) should be extended in order to integrate four instead
of two functions. The full code is listed below:
!========================================================
!Program to solve a 4 ODE system using Runge-Kutta Method
!User must supply derivatives
!dx1/dt=f1(t,x1,x2,x3,x4) dx2/dt=f2(t,x1,x2,x3,x4)
!dx3/dt=f3(t,x1,x2,x3,x4) dx4/dt=f4(t,x1,x2,x3,x4)
!as real(8) functions
!Output is written in file rk2.dat
!========================================================
program rk2_solve
implicit none
integer,parameter :: P=1010000
real(8),dimension(P):: T,X1,X2,V1,V2
real(8) :: Ti,Tf,X10,X20,V10,V20
integer :: Nt, i
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: energy,E0,EF,DE
!Input:
print *,’Runge-Kutta Method for 4-ODEs Integration’
print *,’Enter coupling constants:’
read *, k1,k2
print *,’k1= ’,k1,’ k2= ’,k2
print *,’Enter Nt,Ti,Tf,X10,X20,V10,V20:’
read *, Nt,Ti,TF,X10,X20,V10,V20
print *,’Nt = ’,Nt
print *,’Time: Initial Ti =’,Ti,’ Final Tf=’,Tf
print *,’ X1(Ti)=’,X10,’ X2(Ti)=’,X20
print *,’ V1(Ti)=’,V10,’ V2(Ti)=’,V20
!The Calculation:
call RK(T,X1,X2,V1,V2,Ti,Tf,X10,X20,V10,V20,Nt)
!Output:
open(unit=11,file=’rk2.dat’)
do i=1,Nt
write(11,*)T(i),X1(i),X2(i),V1(i),V2(i),&
energy(T(i),X1(i),X2(i),V1(i),V2(i))
enddo
close(11)
!Rutherford scattering angles:
print *,’v-angle: ’,atan2(V2(Nt),V1(Nt))
print *,’b-angle: ’,2.0D0*atan(k1/(V10*V10*X20))
E0 = energy(Ti ,X10 ,X20 ,V10 ,V20 )
EF = energy(T(Nt),X1(Nt),X2(Nt),V1(Nt),V2(Nt))
DE = ABS(0.5D0*(EF-E0)/(EF+E0))
print *,’E0,EF, DE/E= ’,E0,EF,DE
end program rk2_solve
!========================================================
!The velocity functions f1,f2(t,x1,x2,v1,v2)
!========================================================
real(8) function f1(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
f1=v1 !dx1/dt= v1
end function f1
!--------------------------------------------------------
real(8) function f2(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
f2=v2 !dx2/dt= v2
end function f2
!========================================================
!RK(T,X1,X2,V1,V2,Ti,Tf,X10,X20,V10,V20,Nt) is the driver
!for the Runge-Kutta integration routine RKSTEP
!Input: Initial and final times Ti,Tf
! Initial values at t=Ti X10,X20,V10,V20
! Number of steps of integration: Nt-1
! Size of arrays T,X1,X2,V1,V2
!Output: real arrays T(Nt),X1(Nt),X2(Nt),
! V1(Nt),V2(Nt) where
!T(1) = Ti X1(1) = X10 X2(1) = X20 V1(1) = V10 V2(1) = V20
! X1(k) = X1(at t=T(k)) X2(k) = X2(at t=T(k))
! V1(k) = V1(at t=T(k)) V2(k) = V2(at t=T(k))
!T(Nt)= Tf
!========================================================
subroutine RK(T,X1,X2,V1,V2,Ti,Tf,X10,X20,V10,V20,Nt)
implicit none
integer :: Nt
real(8),dimension(Nt)::T,X1,X2,V1,V2
real(8) :: Ti ,Tf
real(8) :: X10,X20
real(8) :: V10,V20
real(8) :: dt
real(8) :: TS,X1S,X2S !values of time and X1,X2 at given step
real(8) :: V1S,V2S
integer :: i
!Initialize variables:
dt = (Tf-Ti)/(Nt-1)
T (1) = Ti
X1(1) = X10; X2(1) = X20
V1(1) = V10; V2(1) = V20
TS = Ti
X1S = X10; X2S = X20
V1S = V10; V2S = V20
!Make RK steps: The arguments of RKSTEP are
!replaced with the new ones
do i=2,Nt
call RKSTEP(TS,X1S,X2S,V1S,V2S,dt)
T(i) = TS
X1(i) = X1S; X2(i) = X2S
V1(i) = V1S; V2(i) = V2S
enddo
end subroutine RK
!========================================================
!Subroutine RKSTEP(t,x1,x2,dt)
!Runge-Kutta Integration routine of ODE
!dx1/dt=f1(t,x1,x2,x3,x4) dx2/dt=f2(t,x1,x2,x3,x4)
!dx3/dt=f3(t,x1,x2,x3,x4) dx4/dt=f4(t,x1,x2,x3,x4)
!User must supply derivative functions:
!real function f1(t,x1,x2,x3,x4)
!real function f2(t,x1,x2,x3,x4)
!real function f3(t,x1,x2,x3,x4)
!real function f4(t,x1,x2,x3,x4)
!Given initial point (t,x1,x2) the routine advances it
!by time dt.
!Input : Inital time t and function values x1,x2,x3,x4
!Output: Final time t+dt and function values x1,x2,x3,x4
!Careful!: values of t,x1,x2,x3,x4 are overwritten...
!========================================================
subroutine RKSTEP(t,x1,x2,x3,x4,dt)
implicit none
real(8) :: t,x1,x2,x3,x4,dt
real(8) :: f1,f2,f3,f4
real(8) :: k11,k12,k13,k14,k21,k22,k23,k24
real(8) :: k31,k32,k33,k34,k41,k42,k43,k44
real(8) :: h,h2,h6
h =dt !h =dt, integration step
h2=0.5D0*h !h2=h/2
h6=h/6.0D0 !h6=h/6
k11=f1(t,x1,x2,x3,x4)
k21=f2(t,x1,x2,x3,x4)
k31=f3(t,x1,x2,x3,x4)
k41=f4(t,x1,x2,x3,x4)
k12=f1(t+h2,x1+h2*k11,x2+h2*k21,x3+h2*k31,x4+h2*k41)
k22=f2(t+h2,x1+h2*k11,x2+h2*k21,x3+h2*k31,x4+h2*k41)
k32=f3(t+h2,x1+h2*k11,x2+h2*k21,x3+h2*k31,x4+h2*k41)
k42=f4(t+h2,x1+h2*k11,x2+h2*k21,x3+h2*k31,x4+h2*k41)
k13=f1(t+h2,x1+h2*k12,x2+h2*k22,x3+h2*k32,x4+h2*k42)
k23=f2(t+h2,x1+h2*k12,x2+h2*k22,x3+h2*k32,x4+h2*k42)
k33=f3(t+h2,x1+h2*k12,x2+h2*k22,x3+h2*k32,x4+h2*k42)
k43=f4(t+h2,x1+h2*k12,x2+h2*k22,x3+h2*k32,x4+h2*k42)
k14=f1(t+h ,x1+h *k13,x2+h *k23,x3+h *k33,x4+h *k43)
k24=f2(t+h ,x1+h *k13,x2+h *k23,x3+h *k33,x4+h *k43)
k34=f3(t+h ,x1+h *k13,x2+h *k23,x3+h *k33,x4+h *k43)
k44=f4(t+h ,x1+h *k13,x2+h *k23,x3+h *k33,x4+h *k43)
t =t+h
x1=x1+h6*(k11+2.0D0*(k12+k13)+k14)
x2=x2+h6*(k21+2.0D0*(k22+k23)+k24)
x3=x3+h6*(k31+2.0D0*(k32+k33)+k34)
x4=x4+h6*(k41+2.0D0*(k42+k43)+k44)
end subroutine RKSTEP
5.2 Projectile Motion
Consider a particle in the constant gravitational field near the surface of the earth
which moves with constant acceleration  so that
so that
 | (5.2) |
The particle moves on a parabolic trajectory that depends on the initial
conditions
where  is the direction of the initial velocity and
is the direction of the initial velocity and  is the
maximum height of the trajectory.
is the
maximum height of the trajectory.
The acceleration 
 (
( f3 ,
f3 ,  f4) and the
mechanical energy is coded in the file rk2_g.f90:
f4) and the
mechanical energy is coded in the file rk2_g.f90:
!========================================================
!The acceleration functions f3,f4(t,x1,x2,v1,v2) provided
!by the user
!========================================================
!Free fall in constant gravitational filed with
!g = -k2
real(8) function f3(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
f3=0.0D0 !dx3/dt=dv1/dt=a1
end function f3
!--------------------------------------------------------
real(8) function f4(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
f4=-k1 !dx4/dt=dv2/dt=a2
end function f4
!--------------------------------------------------------
real(8) function energy(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
energy = 0.5D0*(v1*v1+v2*v2) + k1*x2
end function energy
In order to calculate a projectile’s trajectory you may use the following
commands:
> gfortran -O2 rk2.f90 rk2_g.f90 -o rk2
> ./rk2
Runge-Kutta Method for 4-ODEs Integration
Enter coupling constants:
10.0 0.0
k1= 10.000000 k2= 0.000000
Enter Nt,Ti,Tf,X10,X20,V10,V20:
20000 0.0 0.2 0.0 0.0 1.0 1.0
Nt= 20000
Time: Initial Ti = 0.000000 Final Tf= 0.200000
X1(Ti)= 0.000000 X2(Ti)= 0.000000
V1(Ti)= 1.000000 V2(Ti)= 1.000000
The analysis of the results contained in the file rk2.dat can be done using
gnuplot:
gnuplot> set terminal x11 1
gnuplot> plot "rk2.dat" using 1:2 with lines title "x(t)"
gnuplot> set terminal x11 2
gnuplot> plot "rk2.dat" using 1:3 with lines title "y(t)"
gnuplot> set terminal x11 3
gnuplot> plot "rk2.dat" using 1:4 with lines title "vx(t)"
gnuplot> set terminal x11 4
gnuplot> plot "rk2.dat" using 1:5 with lines title "vy(t)"
gnuplot> set terminal x11 5
gnuplot> plot "rk2.dat" using 1:($6-1.0) w lines t "E(t)-(0)"
gnuplot> set terminal x11 6
gnuplot> set size square
gnuplot> set title "Trajectory"
gnuplot> plot "rk2.dat" using 2:3 with lines notit
The results can be seen in figures 5.1 and 5.2. We note a small increase in
the mechanical energy which is due to the accumulation of numerical
errors.
We can animate the trajectory by writing a script of gnuplot commands in a
file rk2_animate.gpl
icount = icount+skip
plot "<cat -n rk2.dat" \
using 3:($1<= icount ? $4: 1/0) with lines notitle
# pause 1
if(icount < nlines ) reread
Before calling the script, the user must set the values of the variables
icount, skip and nlines. Each time gnuplot reads the script, it plots
icount number of lines from rk2.dat. Then the script is read again and a
new plot is made with skip lines more than the previous one, unless
icount < nlines. The plotted “file” "<cat -n rk2.dat" is the standard
output (stdout) of the command cat -n rk2.dat which prints to the
stdout the contents of the file rk2.dat line by line, together with the line
number. Therefore the plot command reads data which are the line number,
the time, the coordinate  , the coordinate
, the coordinate  etc. The keyword using
in
etc. The keyword using
in
using 3:($1<= icount ? $4: 1/0)
instructs the plot command to use the 3rd column on the horizontal axis and if
the first column is less than icount ($1<= icount) put on the vertical axis the
value of the 4th column if the first column is less than icount. Otherwise ($1 >
icount) it prints an undefined number (1/0) which makes gnuplot print nothing
at all. You may also uncomment the command pause if you want to make
the animation slower. In order to run the script from gnuplot, issue the
commands
gnuplot> icount = 10
gnuplot> skip = 200
gnuplot> nlines = 20000
gnuplot> load "rk2_animate.gpl"
The scripts shown above can be found in the accompanying software. More
scripts can be found there that automate many of the boring procedures.
The usage of two of these is explained below. The first one is in the file
rk2_animate.csh:
> ./rk2_animate.csh -h
Usage: rk2_animate.csh -t [sleep time] -d [skip points] <file>
Default file is rk2.dat
Other options:
-x: set lower value in xrange
-X: set lower value in xrange
-y: set lower value in yrange
-Y: set lower value in yrange
-r: automatic determination of x-y range
> ./rk2_animate.csh -r -d 500 rk2.dat
The last line is a command that animates a trajectory read from the file
rk2.dat. Each animation frame contains 500 more points than the previous one.
The option -r calculates the plot range automatically. The option -h prints a
short help message.
A more useful script is in the file rk2.csh.
> ./rk2.csh -h
Usage: rk2.csh -f <force> k1 k2 x10 x20 v10 v20 STEPS t0 tf
Other Options:
-n Do not animate trajectory
Available forces (value of <force>):
1: ax=-k1 ay= -k2 y Harmonic oscillator
2: ax= 0 ay= -k1 Free fall
3: ax= -k2 vx ay= -k2 vy - k1 Free fall + \
air resistance ~ v
4: ax= -k2 |v| vx ay= -k2 |v|vy - k1 Free fall + \
air resistance ~ v^2
5: ax= k1*x1/r^3 ay= k1*x2/r^3 Coulomb Force
....
The option -h prints operating instructions. A menu of forces is available, and a
choice can be made using the option -f. The rest of the command line consists of
the parameters read by the program in rk2.f90, i.e. the coupling constants k1,
k2, the initial conditions x10, x20, v10, v20 and the integration parameters
STEPS, t0 and tf. For example, the commands
[literate={-}{{\texttt{-}}}1]
> rk2.csh -f 2 -- 10.0 0.0 0.0 0.0 1.0 1.0 20000 0.0 0.2
> rk2.csh -f 1 -- 16.0 1.0 0.0 1.0 1.0 0.0 20000 0.0 6.29
> rk2.csh -f 5 -- 10.0 0.0 -10 0.2 10. 0.0 20000 0.0 3.00
compute the trajectory of a particle in the constant gravitational field discussed
above, the trajectory of an anisotropic harmonic oscillator (k1 =  ,
k2 =
,
k2 =  ) and the scattering of a particle in a Coulomb field –
try them! I hope that you will have enough curiosity to look “under the
hood” of the scripts and try to modify them or create new ones. Some
advise to the lazy guys: If you need to program your own force field follow
the recipe: Write the code of your acceleration field in a file named e.g.
rk2_myforce.f90 as we did with rk2_g.f90. Edit the file rk2.csh and modify
the line
) and the scattering of a particle in a Coulomb field –
try them! I hope that you will have enough curiosity to look “under the
hood” of the scripts and try to modify them or create new ones. Some
advise to the lazy guys: If you need to program your own force field follow
the recipe: Write the code of your acceleration field in a file named e.g.
rk2_myforce.f90 as we did with rk2_g.f90. Edit the file rk2.csh and modify
the line
set forcecode = (hoc g vg v2g cb)
to
set forcecode = (hoc g vg v2g cb myforce)
(the variable $forcecode may have more entries than the ones shown
above). Count the order of the string myforce, which is 6 in our case. In
order to access this force field from the command line, use the option -f
6:
> rk2.csh -f 6 -- .......
Now, we will study the effect of the air resistance on the motion of the
projectile. For small velocities this is a force proportional to the velocity
 , therefore
, therefore
By taking we obtain the motion of a particle with terminal velocity  (
( const.,
const.,  ).
).
The acceleration caused by the air resistance is programmed in the file (k1
 , k2
, k2  ) rk2_vg.f90:
) rk2_vg.f90:
!========================================================
!The acceleration functions f3,f4(t,x1,x2,v1,v2) provided
!by the user
!========================================================
!Free fall in constant gravitational filed with
!ax = -k2 vx ay = -k2 vy - k1
real(8) function f3(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
f3=-k2*v1 !dx3/dt=dv1/dt=a1
end function f3
!--------------------------------------------------------
real(8) function f4(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
f4=-k2*v2-k1 !dx4/dt=dv2/dt=a2
end function f4
The results are shown in figure 5.3 where we see the effect of an increasing air
resistance on the particle trajectory. The effect of a resistance force of the form
 is shown in figure 5.4.
is shown in figure 5.4.
5.3 Planetary Motion
Consider the simple planetary model of a “sun” of mass  and a planet “earth”
at distance
and a planet “earth”
at distance  from the sun and mass
from the sun and mass  such that
such that  . According to
Newton’s law of gravity, the earth’s acceleration is
. According to
Newton’s law of gravity, the earth’s acceleration is
 | (5.6) |
where  ,
,  ,
,  .
When the hypothesis
.
When the hypothesis  is not valid, the two body problem is reduced to
that of the one body problem with the mass replaced by the reduced mass
is not valid, the two body problem is reduced to
that of the one body problem with the mass replaced by the reduced mass

 The force of gravity is a central force. This implies conservation of the angular
momentum
The force of gravity is a central force. This implies conservation of the angular
momentum  with respect to the center of the force, which in turn
implies that the motion is confined on one plane. We choose the
with respect to the center of the force, which in turn
implies that the motion is confined on one plane. We choose the  axis so
that
axis so
that
 | (5.7) |
The force of gravity is conservative and the mechanical energy
 | (5.8) |
is conserved. If we choose the origin of the coordinate axes to be the center of the
force, the equations of motion (5.6) become
where  . This is a system of two coupled differential equations for the
functions
. This is a system of two coupled differential equations for the
functions  ,
,  . The trajectories are conic sections which are either an
ellipse (bound states - “planet”), a parabola (e.g. escape to infinity when the
particle starts moving with speed equal to the escape velocity) or a hyperbola
(e.g. scattering).
. The trajectories are conic sections which are either an
ellipse (bound states - “planet”), a parabola (e.g. escape to infinity when the
particle starts moving with speed equal to the escape velocity) or a hyperbola
(e.g. scattering).
Kepler’s third law of planetary motion states that the orbital period  of a
planet satisfies the equation
of a
planet satisfies the equation
 | (5.10) |
where  is the semi-major axis of the elliptical trajectory. The eccentricity is a
measure of the deviation of the trajectory from being circular
is the semi-major axis of the elliptical trajectory. The eccentricity is a
measure of the deviation of the trajectory from being circular
 | (5.11) |
where  is the semi-minor axis. The eccentricity is 0 for the circle and tends to 1
as the ellipse becomes more and more elongated. The foci
is the semi-minor axis. The eccentricity is 0 for the circle and tends to 1
as the ellipse becomes more and more elongated. The foci  and
and  are
located at a distance
are
located at a distance  from the center of the ellipse. They have the property
that for every point on the ellipse
from the center of the ellipse. They have the property
that for every point on the ellipse
 | (5.12) |
The acceleration given to the particle by Newton’s force of gravity is
programmed in the file rk2_cb.f90:
!========================================================
!The acceleration functions f3,f4(t,x1,x2,v1,v2) provided
!by the user
!========================================================
!Motion in Coulombic potential:
!ax= k1*x1/r^3 ay= k1*x2/r^3
real(8) function f3(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r2,r3
r2=x1*x1+x2*x2
r3=r2*sqrt(r2)
if(r3.gt.0.0D0)then
f3=k1*x1/r3 !dx3/dt=dv1/dt=a1
else
f3=0.0D0
endif
end function f3
!--------------------------------------------------------
real(8) function f4(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r2,r3
r2=x1*x1+x2*x2
r3=r2*sqrt(r2)
if(r3.gt.0.0D0)then
f4=k1*x2/r3 !dx4/dt=dv2/dt=a2
else
f4=0.0D0
endif
end function f4
!--------------------------------------------------------
real(8) function energy(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r
r=sqrt(x1*x1+x2*x2)
if( r .gt. 0.0D0)then
energy = 0.5D0*(v1*v1+v2*v2) + k1/r
else
energy = 0.0D0
endif
end function energy
We set k1=  and take special care to avoid hitting the center of the
force, the singular point at
and take special care to avoid hitting the center of the
force, the singular point at  . The same code can be used for the
electrostatic Coulomb field with k1=
. The same code can be used for the
electrostatic Coulomb field with k1=  .
.
At first we study trajectories which are bounded. We set  ,
,
 ,
,  ,
,  and vary
and vary  . We measure the period
. We measure the period  and
the length of the semi axes of the resulting ellipse. The results can be found in
table 5.1.
and
the length of the semi axes of the resulting ellipse. The results can be found in
table 5.1.
Some of the trajectories are shown in figure 5.5. There we can see the
dependence of the size of the ellipse on the period. Figure 5.6 confirms Kepler’s
third law of planetary motion given by equation (5.10) .
In order to confirm Kepler’s third law of planetary motion numerically, we
take the logarithm of both sides of equation (5.10)
 | (5.13) |
Therefore, the points  lie on a straight line. Using a linear least
squares fit we calculate the slope and the intercept which should be equal to
lie on a straight line. Using a linear least
squares fit we calculate the slope and the intercept which should be equal to  and
and  respectively. This is left as an exercise.
respectively. This is left as an exercise.
In the case where the initial velocity of the particle becomes larger than the
escape velocity  , the particle escapes from the influence of the gravitational
field to infinity. The escape velocity corresponds to zero mechanical energy, which
gives
, the particle escapes from the influence of the gravitational
field to infinity. The escape velocity corresponds to zero mechanical energy, which
gives
 | (5.14) |
When  ,
,  ,
,  , we obtain
, we obtain 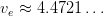 . The
numerical calculation of
. The
numerical calculation of  is left as an exercise.
is left as an exercise.
5.4 Scattering
In this section we consider scattering of particles from a central
potential .
We assume particles that follow unbounded trajectories that start from infinity
and move almost free from the influence of the force field towards its center.
When they approach the region of interaction they get deflected and get
off to infinity in a new direction. We say that the particles have been
scattered and that the angle between their original and final direction is the
scattering angle  . Scattering problems are interesting because we can
infer to the properties of the scattering potential from the distribution of
the scattering angle. This approach is heavily used in today’s particle
accelerators for the study of fundamental interactions between elementary
particles.
. Scattering problems are interesting because we can
infer to the properties of the scattering potential from the distribution of
the scattering angle. This approach is heavily used in today’s particle
accelerators for the study of fundamental interactions between elementary
particles.
First we will discuss scattering of small hard spheres of
radius  by other hard spheres or radius
by other hard spheres or radius  . The interaction
potential
is given by
. The interaction
potential
is given by
 | (5.15) |
where  is the distance between the center of
is the distance between the center of  from the center of
from the center of  .
.
Assume that the particles in the beam do not interact with each other and
that there is only one collision per scattering. Let  be the intensity of the
beam
and
be the intensity of the
beam
and  its cross sectional area. Assume that the target has
its cross sectional area. Assume that the target has  particles per unit
area. The cross sectional area of the interaction is
particles per unit
area. The cross sectional area of the interaction is  where
where  and
and  are the radii of the scattered particles and targets respectively (see figure
(5.8) ): All the spheres of the beam which lie outside this area are not
scattered by the particular target. The total interaction cross section is
are the radii of the scattered particles and targets respectively (see figure
(5.8) ): All the spheres of the beam which lie outside this area are not
scattered by the particular target. The total interaction cross section is
 | (5.16) |
where  is the total number of target spheres which lie within the beam. On
the average, the scattering rate is
is the total number of target spheres which lie within the beam. On
the average, the scattering rate is
 | (5.17) |
The above equation is the definition of the total scattering cross section 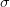 of the interaction. The differential cross section
of the interaction. The differential cross section  is defined by the
relation
is defined by the
relation
 | (5.18) |
where  is the number of particles per unit time scattered within the solid
angle
is the number of particles per unit time scattered within the solid
angle  .
.
The total cross section is
 | (5.19) |
In the last relation we used the cylindrical symmetry of the interaction with
respect to the axis of the collision. Therefore
 | (5.20) |
This relation can be used in experiments for the measurement of the
differential cross section by measuring the rate of detection of particles within
the space contained in between two cones defined by the angles  and
and
 . This is the relation that we will use in the numerical calculation of
. This is the relation that we will use in the numerical calculation of
 .
.
Generally, in order to calculate the differential cross section we shoot a particle
at a target as shown in figure 5.9. The scattering angle  depends on the
impact parameter
depends on the
impact parameter  . The part of the beam crossing the ring of radius
. The part of the beam crossing the ring of radius
 , thickness
, thickness  and area
and area  is scattered in angles between
is scattered in angles between  and
and  . Since there is only one particle at the target we have that
. Since there is only one particle at the target we have that
 . The number of particles per unit time crossing the ring is
. The number of particles per unit time crossing the ring is  ,
therefore
,
therefore
 | (5.21) |
(the  sign is because as
sign is because as  increases,
increases,  decreases). From the potential we can
calculate
decreases). From the potential we can
calculate  and from
and from  we can calculate
we can calculate  . Conversely, if we measure
. Conversely, if we measure
 , we can calculate
, we can calculate  .
.
5.4.1 Rutherford Scattering
The scattering of a charged particle with charge  (“electron”) in a
Coulomb potential of a much heavier charge
(“electron”) in a
Coulomb potential of a much heavier charge  (“nucleus”) is called
Rutherford scattering. In this case, the interaction potential is given by
(“nucleus”) is called
Rutherford scattering. In this case, the interaction potential is given by
 | (5.22) |
which accelerates the particle with acceleration
 | (5.23) |
The energy of the particle is  and the magnitude of its angular
momentum is
and the magnitude of its angular
momentum is  , where
, where  . The dependence of the impact parameter
on the scattering angle is [38]
. The dependence of the impact parameter
on the scattering angle is [38]
 | (5.24) |
Using equation (5.21) we obtain
 | (5.25) |
Consider the scattering trajectories. The results for same charges are shown in
figure 5.10. A similar figure is obtained in the case of opposite charges. In the
latter case we have to take special care for small impact parameters  where the scattering angle is
where the scattering angle is  . A large number of integration steps
is needed in order to obtain the desired accuracy. A useful monitor of
the accuracy of the calculation is the measurement of the energy of the
particle which should be conserved. The results are shown in table 5.2.
. A large number of integration steps
is needed in order to obtain the desired accuracy. A useful monitor of
the accuracy of the calculation is the measurement of the energy of the
particle which should be conserved. The results are shown in table 5.2.
Table 5.3: Rutherford scattering of opposite charges with  . The table is
similar to table 5.2. We observe the numerical difficulty for small impact parameters.
. The table is
similar to table 5.2. We observe the numerical difficulty for small impact parameters.
We will now describe a method for calculating the cross section by
using equation (5.20) . Alternatively we could have used equation (5.21)
and perform a numerical calculation of the derivatives. This is left as an
exercise for the reader. Our calculation is more like an experiment. We
place a “detector” that “detects” particles scattered within angles  and
and  . For this reason we split the interval
. For this reason we split the interval ![[0,π ]](main_latex2345x.png) in
in  bins
so that
bins
so that  . We perform “scattering experiments” by varying
. We perform “scattering experiments” by varying
![b ∈ [bm,bM ]](main_latex2348x.png) with step
with step  . Due to the symmetry of the problem we fix
. Due to the symmetry of the problem we fix  to be a constant, therefore a given
to be a constant, therefore a given  corresponds to a cone with an
opening angle
corresponds to a cone with an
opening angle  and an apex at the center of scattering. For given
and an apex at the center of scattering. For given  we
measure the scattering angle
we
measure the scattering angle  and record the number of particles per unit
time
and record the number of particles per unit
time  . The latter is proportional to the area of the ring of
radius
. The latter is proportional to the area of the ring of
radius  . All we need now is the beam intensity
. All we need now is the beam intensity  which is the total
number of particles per unit time
which is the total
number of particles per unit time  (note than in the ratio
(note than in the ratio
 the proportionality constant and
the proportionality constant and  cancel) and the solid angle
cancel) and the solid angle
 . Finally we can easily use equation (5.19) in order to calculate the
total cross section
. Finally we can easily use equation (5.19) in order to calculate the
total cross section  . The program that performs this calculation is in
the file scatter.f90 and it is a simple modification of the program in
rk2.f90:
. The program that performs this calculation is in
the file scatter.f90 and it is a simple modification of the program in
rk2.f90:
!========================================================
!Program that computes scattering cross-section of a central
!force on the plane. The user should first check that the
!parameters used, lead to a free state in the end.
! ** X20 is the impact parameter b **
!A 4 ODE system is solved using Runge-Kutta Method
!User must supply derivatives
!dx1/dt=f1(t,x1,x2,x3,x4) dx2/dt=f2(t,x1,x2,x3,x4)
!dx3/dt=f3(t,x1,x2,x3,x4) dx4/dt=f4(t,x1,x2,x3,x4)
!as real(8) functions
!Output is written in file scatter.dat
!========================================================
program scatter_cross_section
implicit none
integer,parameter :: P=1010000
real(8),dimension(P):: T,X1,X2,V1,V2
real(8) :: Ti,Tf,X10,X20,V10,V20
real(8) :: X20F,dX20 !max impact parameter and step
integer :: Nt
integer :: i
real(8) :: k1,k2
common /couplings/k1,k2
integer, parameter :: Nbins=20
integer :: index
real(8) :: angle,bins(Nbins),Npart
real(8),parameter :: PI =3.14159265358979324D0
real(8),parameter :: rad2deg=180.0D0/PI
real(8),parameter :: dangle =PI/Nbins
real(8) R,density,dOmega,sigma,sigmatot
!Input:
print *,’Runge-Kutta Method for 4-ODEs Integration’
print *,’Enter coupling constants:’
read *, k1,k2
print *,’k1= ’,k1,’ k2= ’,k2
print *,’Enter Nt,Ti,Tf,X10,X20,V10,V20:’
read *, Nt,Ti,TF,X10,X20,V10,V20
print *,’Enter final impact parameter X20F and step dX20:’
read *, X20F,dX20
print *,’Nt = ’,Nt
print *,’Time: Initial Ti =’,Ti, ’ Final Tf=’,Tf
print *,’ X1(Ti)=’,X10, ’ X2(Ti)=’,X20
print *,’ V1(Ti)=’,V10, ’ V2(Ti)=’,V20
print *,’Impact par X20F =’,X20F,’ dX20 =’,dX20
open(unit=11,file=’scatter.dat’)
bins = 0.0d0
!The Calculation:
Npart = 0.0D0
X20 = X20 + dX20/2.0D0 !starts in middle of first interval
do while (X20 .lt. X20F )
call RK(T,X1,X2,V1,V2,Ti,Tf,X10,X20,V10,V20,Nt)
! Take absolute value due to symmetry:
angle = DABS(atan2(V2(Nt),V1(Nt)))
!Output: The final angle. Check if almost constant
write(11,*) ’@ ’, X20, angle,&
DABS(atan2(V2(Nt-50),V1(Nt-50))),&
k1/V10**2/tan(angle/2.0D0)
!Update histogram:
index = int(angle/dangle)+1
!Number of incoming particles per unit time
!is proportional to radius of ring
!of radius X20, the impact parameter:
!db is cancelled from density
bins(index) = bins(index) + X20
Npart = Npart + X20 !<-- i.e. from here
X20 = X20 + dX20
enddo
!Print scattering cross section:
R = X20 !beam radius
density = Npart/(PI*R*R) !beam flux density J
sigmatot = 0.0D0 !total cross section
do i=1,Nbins
angle = (i-0.5D0)*dangle
dOmega = 2.0D0*PI*sin(angle)*dangle !d(Solid Angle)
sigma = bins(i)/(density*dOmega)
if(sigma.gt.0.0D0) write(11,*) ’ds= ’,&
angle,angle*rad2deg,sigma
sigmatot = sigmatot + sigma*dOmega
enddo
write(11,*) ’sigmatot= ’,sigmatot
close(11)
end program scatter_cross_section
The results are recorded in the file scatter.dat. An example session that
reproduces figures 5.11 and 5.12 is
> gfortran scatter.f90 rk2_cb.f90 -o scatter
> ./scatter
Runge-Kutta Method for 4-ODEs Integration
Enter coupling constants:
1.0 0.0
k1= 1.00000 k2= 0.00000
Enter Nt,Ti,Tf,X10,X20,V10,V20:
5000 0 30 -50 0.02 3 0
Enter final impact parameter X20F and step dX20:
1 0.0002
Nt= 5000
Time: Initial T0 = 0.00000 Final TF= 30.00000
X1(T0)= -50.00000 X2(T0)= 2.00000E-002
V1(T0)= 3.00000 V2(T0)= 0.00000
Impact par X20F = 1.00000 dX20 = 2.00000E-004
The results can be plotted with the gnuplot commands:
gnuplot> set log
gnuplot> plot [:1000] "<grep ds= scatter.dat" \
u ((sin($2/2))**(-4)):($4) notit,\
(1./(4.*3.**4))*x notit
gnuplot> unset log
gnuplot> set log y
gnuplot> plot [:] "<grep ds= scatter.dat" u 2:4 notit, \
(1./(4.*3.**4))*(sin(x/2))**(-4) notit
The results are in a very good agreement with the theoretical ones given by
(5.25) . The next step will be to study other central potentials whose solution is
not known analytically.
5.4.2 More Scattering Potentials
Consider scattering from a force field
 | (5.26) |
This is a very simple classical model of the scattering of a positron  by the
hydrogen atom. The positron has positive charge
by the
hydrogen atom. The positron has positive charge  and the hydrogen atom
consists of a positively charged proton with charge
and the hydrogen atom
consists of a positively charged proton with charge  in an electron
cloud of opposite charge
in an electron
cloud of opposite charge  . We set the scales so that
. We set the scales so that  and
and
 . We will perform a numerical calculation of
. We will perform a numerical calculation of  ,
,  and
and
 .
.
The potential energy is given by
 | (5.27) |
where  for
for  . The program containing the calculation of the
acceleration caused by this force can be found in the file rk_hy.f90:
. The program containing the calculation of the
acceleration caused by this force can be found in the file rk_hy.f90:
!========================================================
!The acceleration functions f3,f4(t,x1,x2,v1,v2) provided
!by the user
!========================================================
!Motion in hydrogen atom + positron:
!f(r) = 1/r^2-r/k1^3
!ax= f(r)*x1/r ay= f(r)*x2/r
real(8) function f3(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r2,r,fr
r2=x1*x1+x2*x2
r =sqrt(r2)
if(r .le.k1 .and. r2.gt.0.0D0)then
fr = 1/r2-r/k1**3
else
fr = 0.0D0
endif
if(fr.gt.0.0D0 .and. r .gt.0.0D0)then
f3=fr*x1/r !dx3/dt=dv1/dt=a1
else
f3=0.0D0
endif
end function f3
!--------------------------------------------------------
real(8) function f4(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r2,r,fr
r2=x1*x1+x2*x2
r =sqrt(r2)
if(r .le.k1 .and. r2.gt.0.0D0)then
fr = 1/r2-r/k1**3
else
fr = 0.0D0
endif
if(fr.gt.0.0D0 .and. r .gt.0.0D0)then
f4=fr*x2/r !dx3/dt=dv1/dt=a1
else
f4=0.0D0
endif
end function f4
!--------------------------------------------------------
real(8) function energy(t,x1,x2,v1,v2)
implicit none
real(8) :: t,x1,x2,v1,v2
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: r,Vr
r=sqrt(x1*x1+x2*x2)
if( r .le.k1 .and. r .gt.0.0D0)then
Vr = 1/r + 0.5D0*r*r/k1**3 - 1.5D0 / k1
else
Vr = 0.0D0
endif
energy = 0.5D0*(v1*v1+v2*v2) + Vr
end function energy
The results are shown in figures 5.13–5.14. We find that  (see
problem 5.10).
(see
problem 5.10).
Another interesting dynamical field is given by the Yukawa potential. This is a
phenomenological model of nuclear interactions:
 | (5.28) |
This field can also be used as a model of the effective interaction of electrons in
metals (Thomas–Fermi) or as the Debye potential in a classic plasma. The
resulting force is
 | (5.29) |
The program of the resulting acceleration can be found in the file rk2_yu.f90.
The results are shown in figures 5.15–5.16.
5.5 More Particles
In this section we will generalize the discussion of the previous paragraphs in the
case of a dynamical system with more degrees of freedom. The number of
dynamical equations that need to be solved depends on the number of degrees of
freedom and we have to write a program that implements the 4th order
Runge–Kutta method for an arbitrary number of equations NEQ. We will explain
how to allocate memory dynamically, in which case the necessary memory storage
space, which depends on NEQ, is allocated at the time of running the program and
not at compilation time.
Until now, memory has been allocated statically. This means that arrays have
sizes which are known at compile time. For example, in the program rk2.f90 the
integer parameter P had a given value which determined the size of all arrays
using the declarations:
integer,parameter :: P=1010000
real(8),dimension(P):: T,X1,X2,V1,V2
Changing P after compilation is impossible and if this becomes necessary we have
to edit the file, change the value of P and recompile. Dynamical memory allocation
allows us to read in Nt and NEQ at execution time and then ask from the
operating system to allocate the necessary memory. All we have to do is to
declare the shape of the arrays (i.e. how many indices they take) and give
them the allocatable attribute. The needed memory can be asked for at
execution time by calling the function ALLOCATE. Here is an example:
integer Nt,NEQ
real(8),allocatable :: T (:) ! Rank-1 array
real(8),allocatable :: X (:,:) ! Rank-2 array
real(8),allocatable :: X0(:) ! Rank-1 array
read *,Nt
call finit(NEQ)
allocate(X0(NEQ))
allocate(T(Nt))
allocate(X(Nt,NEQ))
...
(compute with X0,T,X)
...
deallocate(X0)
deallocate(X )
deallocate(T )
(X0,T,X are not usable anymore)
...
....................
subroutine finit(NEQ)
NEQ = 4
end subroutine finit
In this program the arrays have the allocatable attribute and for each : they
have an extra index. Therefore the arrays T,X0 are rank-1 arrays and
have only one index, whereas the array X is a rank-2 array and has two
indices. The user enters the value of Nt and the subroutine finit sets the
value of NEQ. The calls to the function ALLOCATE allocate the necessary
memory .
If memory allocation is successful, then the arrays can be used in the same way as
the statically allocated ones. When allocatable arrays are not necessary anymore
we should make a call to the function DEALLOCATE which returns the unused
memory back to the system. Otherwise our program might suffer from “memory
leaks” if e.g. the memory is repeatedly asked in a loop that calls a function that
allocates memory without deallocating it in the end. Dynamical memory
allocation is very convenient but for high performance computing static
allocation might be preferable so that the compiler performs a more efficient
optimization.
The main program will be written in the file rkA.f90, whereas the
force-dependent part of the code will be written in files with names of the form
rkA_XXX.f90. In the latter, the user must program a subroutine f(t,X,dXdt)
which takes as input the time t and the values of the functions X(NEQ) and
outputs the values of their derivatives dXdt(NEQ) at time t. The function
finit(NEQ) sets the number of functions in f and it is called once during the
initialization phase of the program.
The program in the file rkA.f90
is listed below:
!========================================================
!Program to solve an ODE system using the
!4th order Runge-Kutta Method
!NEQ: Number of equations
!User supplies two subroutines:
!f(t,x,xdot): with real(8) :: t,x(NEQ),xdot(NEQ) which
!given the time t and current values of functions x(NEQ)
!it returns the values of derivatives: xdot = dx/dt
!The values of two coupling constants k1,k2 may be used
!in f which are read in the main program and stored in
!common /couplings/k1,k2
!finit(NEQ) : sets the value of NEQ
!
!User Interface:
!k1,k2: real(8) coupling constants
!Nt,Ti,Tf: Nt-1 integration steps, initial/final time
!X0: real(8),dimension(NEQ): initial conditions
!Output:
!rkA.dat with Nt lines consisting of: T(Nt),X(Nt,NEQ)
!========================================================
program rk2_solve
implicit none
real(8),allocatable :: T (:)
real(8),allocatable :: X (:,:)
real(8),allocatable :: X0(:)
real(8) :: Ti,Tf
integer :: Nt, NEQ,i
real(8) :: k1,k2
common /couplings/k1,k2
!We need explicit interface, since energy has
!assumed-shape arrays as arguments.
INTERFACE
real(8) function energy(t_intrf,x_intrf)
implicit none
real(8) :: t_intrf,x_intrf(:)
end function energy
END INTERFACE
!Input:
print *,’Runge-Kutta Method for ODE Integration.’
!Get the number of equations:
call finit(NEQ);allocate(X0(NEQ))
print *,’NEQ= ’,NEQ
print *,’Enter coupling constants:’
read *, k1,k2
print *,’k1= ’,k1,’ k2= ’,k2
print *,’Enter Nt,Ti,Tf,X0:’
read *, Nt,Ti,TF,X0
print *,’Nt = ’,Nt
print *,’Time: Initial Ti =’,Ti,’ Final Tf=’,Tf
print ’(A,2000G28.16)’,’ X0 =’,X0
allocate(T(Nt));allocate(X(Nt,NEQ))
!The Calculation:
call RK(T,X,Ti,Tf,X0,Nt,NEQ)
!Output:
open(unit=11,file=’rkA.dat’)
do i=1,Nt
write(11,’(2000G28.16)’)T(i),X(i,:),&
energy(T(i),X(i,:))
enddo
close(11)
end program rk2_solve
!========================================================
!Driver of the RKSTEP routine
!========================================================
subroutine RK(T,X,Ti,Tf,X0,Nt,NEQ)
implicit none
integer :: Nt,NEQ
real(8),dimension(Nt) :: T
real(8),dimension(Nt,NEQ):: X
real(8),dimension(NEQ) :: X0
real(8) :: Ti ,Tf
real(8) :: dt
real(8) :: TS,XS(NEQ) !values of time and X at given step
integer :: i
!Initialize variables:
dt = (Tf-Ti)/(Nt-1)
T (1) = Ti
X (1,:)= X0
TS = Ti
XS = X0
!Make RK steps: The arguments of RKSTEP are
!replaced with the new ones
do i=2,Nt
call RKSTEP(TS,XS,dt,NEQ)
T(i) = TS
X(i,:)= XS
enddo
end subroutine RK
!========================================================
!Subroutine RKSTEP(t,X,dt)
!Runge-Kutta Integration routine of ODE
!========================================================
subroutine RKSTEP(t,x,dt,NEQ)
implicit none
integer :: NEQ
real(8),dimension(NEQ) :: x
real(8) :: t,dt,tt
real(8),dimension(NEQ) :: k1,k2,k3,k4,xx
real(8) :: h,h2,h6
!We need explicit interface, since f has assumed-shape
!arrays as arguments.
INTERFACE
subroutine f(t_intrf,x_intrf,xdot_intrf)
implicit none
real(8) :: t_intrf
real(8),dimension(:):: x_intrf,xdot_intrf
end subroutine f
END INTERFACE
h =dt !h =dt, integration step
h2=0.5D0*h !h2=h/2
h6=h/6.0D0 !h6=h/6
call f(t ,x ,k1); xx = x + h2*k1; tt =t+h2
call f(tt,xx,k2); xx = x + h2*k2; tt =t+h2
call f(tt,xx,k3); xx = x + h *k3; tt =t+h
call f(tt,xx,k4)
t =t+h
x =x +h6*(k1+2.0D0*(k2+k3)+k4)
end subroutine RKSTEP
Note the use of array sections:
write(11,’(2000G28.16)’)T(i),X(i,:)
X(1,:)= X0
X(i,:)= XS
The expression X (1,:) refers to the first row of the array X. The arrays X0 and X
(1,:) are conformable and we can assign the entries in X (1,:) equal to the
entries in X0, i.e. X(1,1)=X0(1), X(1,2)=X0(2), ... , X(1,NEQ)=X0(NEQ) in
only one statement X(1,:)= X0. Similarly the statement write(...) X(i,:)
prints the whole i-th row of the array X whereas the statement X(i,:)= XS
assigns X(i,1)=XS(1), X(i,2)=XS(2), ... , X(i,NEQ)=XS(NEQ). Note the
vector operations:
xx = x + h2* k1
x = x + h6*(k1+2.0D0*(k2+k3)+k4)
which are equivalent to the following do loops
do i=1,NEQ
xx(i) = x(i) + h2* k1(i)
enddo
do i=1,NEQ
x(i) = x(i) + h6*(k1(i)+2.0D0*(k2(i)+k3(i))+k4(i))
enddo
A few words in order to explain what is an INTERFACE block. Up to
now we declared only the type of the functions in the calling program.
When the arguments of the function are arrays for which we only know
their shape and not their size (assumed-shape arrays), the compiler needs
more information. We need to declare the arguments, their types and,
in case they are arrays, their shapes as well. Each program that calls
these functions should include an INTERFACE block which provides this
information. For the functions f and energy, the corresponding INTERFACE block
is
INTERFACE
!-------------------------------------------
subroutine f(t_intrf,x_intrf,xdot_intrf)
implicit none
real(8) :: t_intrf
real(8),dimension(:):: x_intrf,xdot_intrf
end subroutine f
!-------------------------------------------
real(8) function energy(t_intrf,x_intrf)
implicit none
real(8) :: t_intrf,x_intrf(:)
end function energy
!-------------------------------------------
END INTERFACE
You may create files like e.g. interfaces.inc with groups of INTERFACE blocks
and include them in all subprograms that use them with the statement include
"interfaces.inc".
Consider three particles of equal mass exerting a force of gravitational attraction on
each other
like the ones shown in figure 5.17. The forces exerting on each other are given
by
 | (5.30) |
where  and the equations of motion become (
and the equations of motion become ( )
)
where  . The total energy of the system is
. The total energy of the system is
 | (5.32) |
The relations shown above are programmed in the file rkA_3pcb.f90 listed
below:
!===============================
!Sets number of equations
!===============================
subroutine finit(NEQ)
NEQ = 12
end subroutine finit
!===============================
!Three particles of the same
!mass on the plane interacting
!via Coulombic force
!===============================
subroutine f(t,X,dXdt)
implicit none
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: t,X(:),dXdt(:)
!-----------------------
real(8) :: x11,x12,x21,x22,x31,x32
real(8) :: v11,v12,v21,v22,v31,v32
real(8) :: r12,r13,r23
!-----------------------
x11 = X(1);x21 = X(5);x31 = X(9)
x12 = X(2);x22 = X(6);x32 = X(10)
v11 = X(3);v21 = X(7);v31 = X(11)
v12 = X(4);v22 = X(8);v32 = X(12)
!-----------------------
r12 = ((x11-x21)*(x11-x21)+(x12-x22)*(x12-x22))**(-1.5D0)
r13 = ((x11-x31)*(x11-x31)+(x12-x32)*(x12-x32))**(-1.5D0)
r23 = ((x21-x31)*(x21-x31)+(x22-x32)*(x22-x32))**(-1.5D0)
!--------------
dXdt(1) = v11
dXdt(2) = v12
dXdt(3) = k1*(x11-x21)*r12+k1*(x11-x31)*r13 ! a11=dv11/dt
dXdt(4) = k1*(x12-x22)*r12+k1*(x12-x32)*r13 ! a12=dv12/dt
!--------------
dXdt(5) = v21
dXdt(6) = v22
dXdt(7) = k1*(x21-x11)*r12+k1*(x21-x31)*r23 ! a21=dv21/dt
dXdt(8) = k1*(x22-x12)*r12+k1*(x22-x32)*r23 ! a22=dv22/dt
!--------------
dXdt(9) = v31
dXdt(10) = v32
dXdt(11) = k1*(x31-x11)*r13+k1*(x31-x21)*r23 ! a31=dv31/dt
dXdt(12) = k1*(x32-x12)*r13+k1*(x32-x22)*r23 ! a32=dv32/dt
end subroutine f
!===============================
real(8) function energy(t,X)
implicit none
real(8) :: k1,k2
common /couplings/k1,k2
real(8) :: t,X(:)
!-----------------------
real(8) :: x11,x12,x21,x22,x31,x32
real(8) :: v11,v12,v21,v22,v31,v32
real(8) :: r12,r13,r23
!-----------------------
x11 = X(1);x21 = X(5);x31 = X(9)
x12 = X(2);x22 = X(6);x32 = X(10)
v11 = X(3);v21 = X(7);v31 = X(11)
v12 = X(4);v22 = X(8);v32 = X(12)
!-----------------------
r12 = ((x11-x21)*(x11-x21)+(x12-x22)*(x12-x22))**(-0.5D0)
r13 = ((x11-x31)*(x11-x31)+(x12-x32)*(x12-x32))**(-0.5D0)
r23 = ((x21-x31)*(x21-x31)+(x22-x32)*(x22-x32))**(-0.5D0)
!-----------------------
energy = 0.5D0*&
(v11*v11+v12*v12+v21*v21+v22*v22+v31*v31+v32*v32)
energy = energy + k1*(r12+r13+r23)
end function energy
In order to run the program and see the results look at the commands in
the shell script in the file rkA_3pcb.csh. In order to run the script use
command
> rkA_3pcb.csh -0.5 4000 1.5 -1 0.1 1 0 1 -0.1 -1 0 0.05 1 0 -1
which will run the program setting  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  , Nt
, Nt and
and  .
.
5.6 Problems
- Reproduce the results shown in figures 5.3 and 5.4. Compare your
results to the known analytic solution.
- Write a program for the force on a charged particle in a
constant magnetic field
 and compute its trajectory for
and compute its trajectory for
 . Set
. Set  and calculate the
resulting radius of the trajectory. Plot the relation between the radius
and
and calculate the
resulting radius of the trajectory. Plot the relation between the radius
and  . Compare your results to the known analytic solution. (assume
non relativistic motion)
. Compare your results to the known analytic solution. (assume
non relativistic motion)
- Consider the anisotropic
harmonic oscillator
 ,
,  . Construct the Lissajous
curves by setting
. Construct the Lissajous
curves by setting  ,
,  ,
,
 ,
,  . What happens when
. What happens when  ?
?
- Reproduce the results displayed in table 5.1 and figures 5.5 and 5.6.
Plot
 vs
vs  and calculate the slope of the resulting straight
line by using the linear least squares method. Is it what you expect?
Calculate the intercept and compare your result with the expected one.
and calculate the slope of the resulting straight
line by using the linear least squares method. Is it what you expect?
Calculate the intercept and compare your result with the expected one.
- Calculate the angular momentum with respect to the center of the force
at each integration step of the planetary motion and check whether it is
conserved. Show analytically that conservation of angular momentum
implies that the position vector sweeps areas at constant rate.
- Calculate the escape velocity of a planet
 for
for  ,
,
 ,
,  using the following steps: First show
that
using the following steps: First show
that  . Then set
. Then set  ,
,  . Vary
. Vary
 and measure the resulting semi-major axis
and measure the resulting semi-major axis  . Determine
the intercept of the resulting straight line in order to calculate
. Determine
the intercept of the resulting straight line in order to calculate  .
.
- Repeat the previous problem for
 ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  . From the
. From the  plot confirm the relation
(5.14) .
plot confirm the relation
(5.14) .
- Check that for the bound trajectory of a planet with
 ,
,
 ,
,  ,
,  ,
,  you obtain that
you obtain that
 for each point
for each point  of the trajectory. The point
of the trajectory. The point  is the center of the force. After determining the semi-major axis
is the center of the force. After determining the semi-major axis  numerically, the point
numerically, the point  will be taken symmetric to
will be taken symmetric to  with respect
to the center of the ellipse.
with respect
to the center of the ellipse.
- Consider the planetary motion studied in the previous problem. Apply
a momentary push in the tangential direction after the planet has
completed 1/4 of its elliptical orbit. How stable is the particle trajectory
(i.e. what is the dependence of the trajectory on the magnitude and
the duration of the push?)? Repeat the problem when the push is in
the vertical direction.
- Consider the scattering potential of the positron-hydrogen system
given by equation (5.26) . Plot the functions
 and
and  for
different values of
for
different values of  . Calculate the total cross section
. Calculate the total cross section  numerically
and show that it is equal to
numerically
and show that it is equal to  .
.
- Consider the Morse potential of diatomic molecules:
 | (5.33) |
where  . Compute the solutions of the problem numerically in one
dimension and compare them to the known analytic solutions when
. Compute the solutions of the problem numerically in one
dimension and compare them to the known analytic solutions when
 :
:
 | (5.34) |
where the integration constant as a function of the initial position and
energy is given by
![[ αx0 ]
C = sin−1 ∘D--−-|E|e----- .
D(D − |E|)](main_latex2476x.png) | (5.35) |
We obtain a periodic motion with an energy dependent period
 . For
. For  we obtain
we obtain
 | (5.36) |
whereas for 
 | (5.37) |
In these equations, the integration constant  is given by a different
relation and not by equation (5.35) . Compute the motion in phase space
is given by a different
relation and not by equation (5.35) . Compute the motion in phase space
 and study the transition from open to closed trajectories.
and study the transition from open to closed trajectories.
- Consider the effective potential term
 (
( ) in the
previous problem. Plot the function
) in the
previous problem. Plot the function  for
for  ,
,
 ,
,  ,
,  , and of course for
, and of course for  . Determine the
equilibrium position and the ionization energy.
. Determine the
equilibrium position and the ionization energy.
Calculate the solutions  ,
,  ,
,  ,
,  on the plane for
on the plane for  ,
,
 , and
, and  numerically. In the
numerically. In the  case consider the scattering
problem and calculate the functions
case consider the scattering
problem and calculate the functions  ,
,  and the total cross section
and the total cross section
 .
.
- Consider the potential of the molecular model given by the force
 where
where  . Calculate the potential
. Calculate the potential
 and plot the function
and plot the function  . Determine the
equilibrium position and the ionization energy.
. Determine the
equilibrium position and the ionization energy.
Consider the problem of scattering and calculate  ,
,  and
and  numerically. How much do your results depend on the minimum scattering
angle?
numerically. How much do your results depend on the minimum scattering
angle?
- Compute the trajectories of a particle under the influence of a force
 . Determine appropriate initial conditions that give a spiral
trajectory.
. Determine appropriate initial conditions that give a spiral
trajectory.
- Compute the total cross section
 for the Rutherford scattering both
analytically and numerically. What happens to your numerical results as you
vary the integration limits?
for the Rutherford scattering both
analytically and numerically. What happens to your numerical results as you
vary the integration limits?
- Write a program that computes the trajectory of a particle that
moves on the plane in the static electric field of
 static point
charges.
static point
charges.
- Solve the three body problem described in the text in the case of three
different electric charges by making the appropriate changes to the program
in the file rkA_3cb.f90.
- Two charged particles of equal mass and charge are moving on the
 plane in a constant magnetic field
plane in a constant magnetic field  . Solve the equations of motion
using a 4th order Runge–Kutta Method. Plot the resulting trajectories for
the initial conditions that you will choose.
. Solve the equations of motion
using a 4th order Runge–Kutta Method. Plot the resulting trajectories for
the initial conditions that you will choose.
- Three particles of equal mass
 are connected by identical springs. The
springs’ spring constant is equal to
are connected by identical springs. The
springs’ spring constant is equal to  and their equilibrium length is equal
to
and their equilibrium length is equal
to  . The particles move without friction on a horizontal plane. Solve the
equations of motion of the system numerically by using a 4th order
Runge–Kutta Method. Plot the resulting trajectories for the initial
conditions that you will choose. (Hint: Look in the files rkA_3hoc.f90,
rkA_3hoc.csh.)
. The particles move without friction on a horizontal plane. Solve the
equations of motion of the system numerically by using a 4th order
Runge–Kutta Method. Plot the resulting trajectories for the initial
conditions that you will choose. (Hint: Look in the files rkA_3hoc.f90,
rkA_3hoc.csh.)
- Two identical particles are attached to thin weightless rods of length
 and they are connected by an ideal weightless spring with spring
constant
and they are connected by an ideal weightless spring with spring
constant  and equilibrium length
and equilibrium length  . The rods are hinged to the
ceiling at points whose distance is
. The rods are hinged to the
ceiling at points whose distance is  (see figure 5.18). Compute
the Lagrangian of the system and the equations of motion for the
degrees of freedom
(see figure 5.18). Compute
the Lagrangian of the system and the equations of motion for the
degrees of freedom  and
and  . Solve these equations numerically by
using a 4th order Runge–Kutta method. Plot the positions of the
particles in a Cartesian coordinate system and the resulting trajectory.
Study the normal modes for small angles
. Solve these equations numerically by
using a 4th order Runge–Kutta method. Plot the positions of the
particles in a Cartesian coordinate system and the resulting trajectory.
Study the normal modes for small angles  and compute the
deviation of the solutions from the small oscillation approximation as
the angles become larger. (Hint: Look in the files rk_cpend.f90,
rk_cpend.csh)
and compute the
deviation of the solutions from the small oscillation approximation as
the angles become larger. (Hint: Look in the files rk_cpend.f90,
rk_cpend.csh)
- Repeat the previous problem when the hinges of the rods slide without
friction on the
 axis.
axis.
- Repeat problem 5.20 by adding a third pendulum to the right at distance
 .
.
Chapter 6
Motion in Space
In this chapter we will study the motion of a
particle in space (three dimensions). We will also discuss the case of the
relativistic motion, which is important if one wants to consider the motion of
particles moving with speeds comparable to the speed of light. This will be an
opportunity to use an adaptive stepsize Runge-Kutta method for the numerical
solution of the equations of motion. We will use the open source code
rksuite available
at the Netlib
repository. Netlib is an open source, high quality repository for numerical analysis
software. The software it contains is used by many researchers in their high
performance computing programs and it is a good investment of time to learn how
to use it.
The technical skill that you will exercise in this chapter is looking for solutions to
your numerical problems provided by software written by others. It is
important to be able to locate the optimal solution to your problem, find the
relevant functions, read the software’s documentation carefully and filter out
the necessary information in order to call and link the functions to your
program.
6.1 Adaptive Stepsize Control for Runge–Kutta Methods
The three dimensional equation of motion of a particle is an initial value problem
given by the equations (4.6)

For its numerical solution we will use an adaptive stepsize Runge–Kutta
algorithm for increased performance and accuracy. Adaptive stepsize is used in
cases where one needs to minimize computational effort for given accuracy goal.
The method frequently changes the time step during the integration process, so
that it is set to be large through smooth intervals and small when there
are abrupt changes in the values of the functions. This is achieved by
exercising error control either by monitoring a conserved quantity or by
computing the same solution using two different methods. In our case, two
Runge-Kutta methods are used, one of order  and one of order
and one of order  ,
and the difference of the results is used as an estimate of the truncation
error. If the error needs to be reduced, the step size is reduced and if it is
satisfactorily small the step size is increased. For the details we refer the
reader to [31]. Our goal is not to analyze and understand the details of
the algorithm, but to learn how to find and use appropriate and high
quality code written by others. The link http://www.netlib.org/ode/
reads
,
and the difference of the results is used as an estimate of the truncation
error. If the error needs to be reduced, the step size is reduced and if it is
satisfactorily small the step size is increased. For the details we refer the
reader to [31]. Our goal is not to analyze and understand the details of
the algorithm, but to learn how to find and use appropriate and high
quality code written by others. The link http://www.netlib.org/ode/
reads
lib rksuite
alg Runge-Kutta
for initial value problem for first order ordinary differential
equations. A suite of codes for solving IVPs in ODEs. A
choice of RK methods, is available. Includes an error
assessment facility and a sophisticated stiffness checker.
Template programs and example results provided.
Supersedes RKF45, DDERKF, D02PAF.
ref RKSUITE, Softreport 92-S1, Dept of Math, SMU, Dallas, Texas
by R.W. Brankin (NAG), I. Gladwell and L.F. Shampine (SMU)
lang Fortran
prec double
There, we learn that the package provides code for Runge–Kutta methods, whose
source is open and written in the Fortran language. We also learn that the code is
written for double precision variables, which is suitable for our problem. Last, but
not least, we are also happy to learn that it is written by highly reputable people!
We download the files rksuite.f, rksuite.doc, details.doc, templates,
readme.
In order to link the subroutines provided by the suite to our program we need
to read the documentation carefully. In the general case, documentation is
available on the web (html, pdf, ...), bundled files with names like README,
INSTALL, in whole directories with names like doc/, online help in man or info
pages and finally in good old fashioned printed manuals. Good quality software is
also well documented inside the source code files, something that is true for the
software at hand.
In order to link the suite’s subroutines to our program we need the following
basic information:
- INPUT DATA: This is the necessary information that the program
needs in order to perform the calculation. In our case, the minimal
such information is the initial conditions, the integration time interval
and the number of integration steps. The user should also provide the
functions on the right hand side of (6.1) . It might also be necessary to
provide information about the desired accuracy goal, the scale of the
problem, the hardware etc.
- OUTPUT DATA: This is the information on how we obtain the
results of the calculation for further analysis. Information whether the
calculation was successful and error free could also be provided.
- WORKSPACE: This is information on how we provide the necessary
memory space used in the intermediate calculations. Such space needs
to be provided by the user in programming languages where dynamical
memory allocation is not possible, like in Fortran 77, and the size of
workspace depends on the parameters of the calling program.
It is easy to install the software. All the necessary code is in one file rksuite.f. The file
rksuite.doc
contains the documentation. There we read that we need to inform the program
about the hardware dependent accuracy of floating point numbers. We need to set
the values of three variables:
...
RKSUITE requires three environmental constants OUTCH, MCHEPS,
DWARF. When you use RKSUITE, you may need to know their
values. You can obtain them by calling the subroutine ENVIRN
in the suite:
CALL ENVIRN(OUTCH,MCHPES,DWARF)
returns values
OUTCH - INTEGER
Standard output channel on the machine being used.
MCHEPS - DOUBLE PRECISION
The unit of roundoff, that is, the largest
positive number such that 1.0D0 + MCHEPS = 1.0D0.
DWARF - DOUBLE PRECISION
The smallest positive number on the machine being
used.
...
************************** Installation Details ************
All machine-dependent aspects of the suite have been
isolated in the subroutine ENVIRN in the rksuite.for file.
Certain environmental parameters must be specified in this
subroutine. The values in the distribution version are
those appropriate to the IEEE arithmetic standard. They
must be altered, if necessary, to values appropriate to the
computing system you are using before calling the codes of
the suite. If the IEEE arithmetic standard values are not
appropriate for your system, appropriate values can often
be obtained by calling routines named in the Comments of
ENVIRN.
...
The variables OUTCH, MCHEPS, DWARF are defined in the subroutine ENVIRN. They
are given generic default values but the programmer is free to change them by editing
ENVIRN. We should identify the routine in the file rksuite.f and read the comments
in it :
...
SUBROUTINE ENVIRN(OUTCH,MCHEPS,DWARF)
...
C The following six statements are to be Commented out
C after verification that the machine and installation
C dependent quantities are specified correctly.
...
WRITE(*,*) ’ Before using RKSUITE, you must verify that the ’
WRITE(*,*) ’ machine- and installation-dependent quantities ’
WRITE(*,*) ’ specified in the subroutine ENVIRN are correct, ’
WRITE(*,*) ’ and then Comment these WRITE statements and the ’
WRITE(*,*) ’ STOP statement out of ENVIRN. ’
STOP
...
C The following values are appropriate to IEEE
C arithmetic with the typical standard output channel.
C
OUTCH = 6
MCHEPS = 1.11D-16
DWARF = 2.23D-308
All we need to do is to comment out the WRITE and STOP commands since we will
keep the default values of the OUTCH, MCHEPS, DWARF variables:
...
C WRITE(*,*) ’ Before using RKSUITE, you must verify that the ’
C WRITE(*,*) ’ machine- and installation-dependent quantities ’
C WRITE(*,*) ’ specified in the subroutine ENVIRN are correct, ’
C WRITE(*,*) ’ and then Comment these WRITE statements and the ’
C WRITE(*,*) ’ STOP statement out of ENVIRN. ’
C STOP
...
In order to check whether the default values are satisfactory, we can use the
Fortran intrinsic functions EPSILON() and TINY(). In the file test_envirn.f90,
we write a small test program
program testme
implicit none
integer :: OUTCH
real(8) :: DWARF, MCHEPS
real(8) :: x
OUTCH = 6 !This is pretty much a standard
MCHEPS = epsilon(x)/2.0D0
DWARF = tiny(x)
write(6,101)OUTCH,MCHEPS,DWARF
101 format(I4,2E30.18)
end program testme
We compile and run the above program as follows:
> gfortran test_envirn.f90 -o test_envirn
> ./test_envirn
6 0.111022302462515654E-15 0.222507385850720138-307
We conclude that our choices are satisfactory.
Next we need to learn how to use the subroutines in the suite. By carefully
reading rksuite.doc we learn the following: The interface to the adaptive
stepsize Runge–Kutta algorithm is the routine UT (UT = “Usual Task”). The
routine can use a 2nd-3rd (RK23) order Runge-Kutta pair for error control
(METHOD=1), a 4th-5th (RK45) order pair (METHOD=2) or a 7th-8th (RK78) order
pair (METHOD=3). We will set METHOD=2 (RK45). The routine SETUP must be called
before UT for initialization. The user should provide a function F that calculates
the derivatives of the functions we integrate for, i.e. the right hand side of
6.1.
The fastest way to learn how to use the above routines is “by example”. The
suite include a templates package which can be unpacked by executing the
commands in the file templates using the sh shell:
> sh templates
tmpl1.out
tmpl1a.f
...
The file tmpl1a.f contains the solution of the simple harmonic oscillator and has
many explanatory comments in it. We encourage the reader to study it carefully,
run it and test its results.
After we become wise enough, we write the driver for the integration routine
UT, which can be found in the file rk3.f90:
!========================================================
!Program to solve a 6 ODE system using Runge-Kutta Method
!Output is written in file rk3.dat
!========================================================
program rk3_solve
include ’rk3.inc’
real(8) :: T0,TF,X10,X20,X30,V10,V20,V30
real(8) :: t,dt,tstep
integer :: STEPS
integer :: i
real(8) :: energy
!Arrays/variables needed by rksuite:
real(8) TOL,THRES(NEQ),WORK(LENWRK),Y(NEQ),YMAX(NEQ),&
YP(NEQ),YSTART(NEQ),HSTART
logical ERRASS, MESSAGE
integer UFLAG
!.. External Subroutines ..
EXTERNAL F, SETUP, STAT, UT
!Input:
print *,’Runge-Kutta Method for 6-ODEs Integration’
print *,’Enter coupling constants k1,k2,k3,k4:’
read *, k1,k2,k3,k4
print *,’k1= ’,k1,’ k2= ’,k2,’ k3= ’,k3,’ k4= ’,k4
print *,’Enter STEPS,T0,TF,X10,X20,X30,V10,V20,V30:’
read *, STEPS,T0,TF,X10,X20,X30,V10,V20,V30
print *,’No. Steps= ’,STEPS
print *,’Time: Initial T0 =’,T0,’ Final TF=’,TF
print *,’ X1(T0)=’,X10,’ X2(T0)=’,X20,’ X3(T0)=’,X30
print *,’ V1(T0)=’,V10,’ V2(T0)=’,V20,’ V3(T0)=’,V30
!Initial Conditions
dt = (TF-T0)/STEPS
YSTART(1) = X10
YSTART(2) = X20
YSTART(3) = X30
YSTART(4) = V10
YSTART(5) = V20
YSTART(6) = V30
!
! Set error control parameters.
!
TOL = 5.0D-6
do i = 1, NEQ
THRES(i) = 1.0D-10
enddo
MESSAGE = .TRUE.
ERRASS = .FALSE.
HSTART = 0.0D0
!Initialization:
call SETUP(NEQ,T0,YSTART,TF,TOL,THRES,METHOD,’Usual Task’,&
ERRASS,HSTART,WORK,LENWRK,MESSAGE)
open(unit=11,file=’rk3.dat’)
write(11,100) T0,YSTART(1),YSTART(2),YSTART(3),YSTART(4),&
YSTART(5),YSTART(6),energy(T0,YSTART)
!Calculation:
do i=1,STEPS
t = T0 + i*dt
call UT(F,t,tstep,Y,YP,YMAX,WORK,UFLAG)
if(UFLAG.GT.2) exit !exit the loop: go after enddo
write(11,100) tstep,Y(1),Y(2),Y(3),Y(4),Y(5),Y(6),&
energy(tstep,Y)
enddo
close(11)
100 format(8E25.15)
end program rk3_solve
All common parameters and variables are declared in an include file rk3.inc.
This is necessary in order for them to be accessible by the function F which
calculates the derivatives. The contents of this file are substituted in each line
containing the command include ’rk3.inc’.
!Basic definitions of variables for the suite rksuite
implicit none
!NEQ is the number of equations, 6 in 3 dimensions
!METHOD=2 is for RK45.
INTEGER NEQ, LENWRK, METHOD
PARAMETER (NEQ=6,LENWRK=32*NEQ,METHOD=2)
REAL *8 k1,k2,k3,k4 !force couplings
COMMON /COUPLINGS/k1,k2,k3,k4
The number of differential equations is set equal to NEQ=6. The integration
method is set by the choice METHOD=2. The variable LENWRK sets the size of the
workspace needed by the suite for the intermediate calculations.
The main program starts with the user interface. The initial state of the
particle is stored in the array YSTART in the positions  . The first three
positions are the coordinates of the initial position and the last three
the components of the initial velocity. Then we set some variables that
determine the behavior of the integration program (see the file rksuite.doc
for details) and call the subroutine SETUP. The main integration loop
is:
. The first three
positions are the coordinates of the initial position and the last three
the components of the initial velocity. Then we set some variables that
determine the behavior of the integration program (see the file rksuite.doc
for details) and call the subroutine SETUP. The main integration loop
is:
do i=1,STEPS
t = T0 + i*dt
call UT(F,t,tstep,Y,YP,YMAX,WORK,UFLAG)
if(UFLAG.GT.2) exit !exit the loop: go after enddo
write(11,100) tstep,Y(1),Y(2),Y(3),Y(4),Y(5),Y(6),&
energy(tstep,Y)
enddo
The function F is the subroutine that calculates the derivatives and
it will be programmed by us later. The variable t stores the desired
moment of time at which we want to calculate the functions. Because
of the adaptive stepsize, it can be different than the one returned
by the subroutine UT. The actual value of time that the next step
lands
on is tstep. The array Y stores the values of the functions. We choose the data
structure to be such that  = Y(1),
= Y(1),  = Y(2),
= Y(2),  = Y(3) and
= Y(3) and  = Y(4),
= Y(4),  =
Y(5),
=
Y(5),  = Y(6) (the same sequence as in the array YSTART). The function
energy(t,Y) returns the value of the mechanical energy of the particle and its
code will be written in the same file as that of F. Finally, the variable UFLAG
indicates the error status of the calculation by UT and if UFLAG
= Y(6) (the same sequence as in the array YSTART). The function
energy(t,Y) returns the value of the mechanical energy of the particle and its
code will be written in the same file as that of F. Finally, the variable UFLAG
indicates the error status of the calculation by UT and if UFLAG we end the
calculation.
we end the
calculation.
Our test code will be on the study of the motion of a projectile in a
constant gravitational field, subject also to the influence of a dissipative force
 . The program is in the file rk3_g.f90. We choose the parameters k1
and k2 so that
. The program is in the file rk3_g.f90. We choose the parameters k1
and k2 so that  -k1
-k1  and
and  k2.
k2.
!---------------------------------
subroutine F(T,Y,YP)
include ’rk3.inc’
real(8) :: t
real(8) :: Y(*),YP(*)
real(8) :: x1,x2,x3,v1,v2,v3
x1 = Y(1);v1 = Y(4)
x2 = Y(2);v2 = Y(5)
x3 = Y(3);v3 = Y(6)
!Velocities: dx_i/dt = v_i
YP(1) = v1
YP(2) = v2
YP(3) = v3
!Acceleration: dv_i/dt = a_i
YP(4) = -k2*v1
YP(5) = -k2*v2
YP(6) = -k2*v3-k1
end subroutine F
!---------------------------------
real(8) function energy(T,Y)
include ’rk3.inc’
real(8) :: t,e
real(8) :: Y(*)
real(8) :: x1,x2,x3,v1,v2,v3
x1 = Y(1);v1 = Y(4)
x2 = Y(2);v2 = Y(5)
x3 = Y(3);v3 = Y(6)
!Kinetic Energy
e = 0.5*(v1*v1+v2*v2+v3*v3)
!Potential Energy
e = e + k1*x3
energy = e
end function energy
For convenience we “translated” the values in the array Y(NEQ) into user-friendly variable
names .
If the file rksuite.f is in the directory rksuite/, then the compilation, running
and visualization of the results can be done with the commands:
> gfortran rk3.f90 rk3_g.f90 rksuite/rksuite.f -o rk3
> ./rk3
Runge-Kutta Method for 6-ODEs Integration
Enter coupling constants k1,k2,k3,k4:
10 0 0 0
k1= 10.0000 k2= 0.0000E+000 k3=
0.0000E+000 k4= 0.0000E+000
Enter STEPS,T0,TF,X10,X20,X30,V10,V20,V30:
10000 0 3 0 0 0 1 1 1
No. Steps= 10000
Time: Initial T0 = 0.0000E+000 Final TF= 3.0000
X1(T0)= 0.0000E+000 X2(T0)= 0.0000E+000
X3(T0)= 0.0000E+000
V1(T0)= 1.0000 V2(T0)= 1.0000
V3(T0)= 1.0000
> gnuplot
gnuplot> plot "rk3.dat" using 1:2 with lines title "x1(t)"
gnuplot> plot "rk3.dat" using 1:3 with lines title "x2(t)"
gnuplot> plot "rk3.dat" using 1:4 with lines title "x3(t)"
gnuplot> plot "rk3.dat" using 1:5 with lines title "v1(t)"
gnuplot> plot "rk3.dat" using 1:6 with lines title "v2(t)"
gnuplot> plot "rk3.dat" using 1:7 with lines title "v3(t)"
gnuplot> plot "rk3.dat" using 1:8 with lines title "E(t)"
gnuplot> set title "trajectory"
gnuplot> splot "rk3.dat" using 2:3:4 with lines notitle
All the above commands can be executed together using the shell script in the file
rk3.csh. The script uses the animation script rk3_animate.csh. The following
command executes all the commands shown above:
./rk3.csh -f 1 -- 10 0. 0 0 0 0 0 1 1 1 10000 0 3
6.2 Motion of a Particle in an EM Field
In this section we study the non-relativistic motion of a charged particle in an
electromagnetic (EM) field. The particle is under the influence of the Lorentz
force:
 | (6.2) |
Consider the constant EM field of the form  ,
,  .
The components of the acceleration of the particle are:
.
The components of the acceleration of the particle are:
This field is programmed in the file rk3_B.f90. We set k1  , k2
, k2
 , k3
, k3  and k4
and k4  :
:
!------------------------------------------------
!Particle in constant Magnetic and electric field
!q B/m = k1 z q E/m = k2 x + k3 y + k4 z
subroutine F(T,Y,YP)
include ’rk3.inc’
real(8) :: t
real(8) :: Y(*),YP(*)
real(8) :: x1,x2,x3,v1,v2,v3
x1 = Y(1);v1 = Y(4)
x2 = Y(2);v2 = Y(5)
x3 = Y(3);v3 = Y(6)
!Velocities: dx_i/dt = v_i
YP(1) = v1
YP(2) = v2
YP(3) = v3
!Acceleration: dv_i/dt = a_i
YP(4) = k2 + k1 * v2
YP(5) = k3 - k1 * v1
YP(6) = k4
end subroutine F
!---------------------------------
real(8) function energy(T,Y)
include ’rk3.inc’
real(8) :: t,e
real(8) :: Y(*)
real(8) :: x1,x2,x3,v1,v2,v3
x1 = Y(1);v1 = Y(4)
x2 = Y(2);v2 = Y(5)
x3 = Y(3);v3 = Y(6)
!Kinetic Energy
e = 0.5*(v1*v1+v2*v2+v3*v3)
!Potential Energy
e = e - k2*x1 - k3*x2 - k4*x3
energy = e
end function energy
We can also study space-dependent fields in the same way. The fields must
satisfy Maxwell’s equations. We can study the confinement of a particle in
a region of space by a magnetic field by taking  with
with
 ,
,  and
and  ,
,  .
Note that
.
Note that  . You may also want to calculate the current density from
the equation
. You may also want to calculate the current density from
the equation  .
.
The results are shown in figures 6.1–6.4.
6.3 Relativistic Motion
Consider a particle of non zero rest mass moving with speed
comparable to the speed of light. In this case, it is necessary to
study its motion using the equations of motion given by special
relativity .
In the equations below we set  . The particle’s rest mass is
. The particle’s rest mass is  , its
mass is
, its
mass is  (where
(where  ), its momentum is
), its momentum is  and its
energy is
and its
energy is  . Then the equations of motion in a dynamic field
. Then the equations of motion in a dynamic field
 are given by:
are given by:
 | (6.4) |
In order to write a system of first order equations, we use the relations
 | (6.5) |
Using  we obtain
we obtain
which is a system of first order differential equations for the functions 




 . Given the initial conditions
. Given the initial conditions





 their solution is
unique and it can be computed numerically using the 4th-5th order Runge–Kutta
method according to the discussion of the previous section. By using the relations
we can use the initial conditions
their solution is
unique and it can be computed numerically using the 4th-5th order Runge–Kutta
method according to the discussion of the previous section. By using the relations
we can use the initial conditions  ,
,  ,
,  ,
,  ,
,  ,
,  instead. Similarly, from the solutions
instead. Similarly, from the solutions  ,
,  ,
,  ,
,  ,
,
 ,
,  we can calculate
we can calculate  ,
,  ,
,  ,
,  ,
,  ,
,
 . We always have to check that
. We always have to check that
 | (6.8) |
Since half of the functions that we integrate for are the momentum instead of
the velocity components, we need to make some modifications to the
program in the file rk3.f90. The main program can be found in the file
sr.f90:
!========================================================
!Program to solve a 6 ODE system using Runge-Kutta Method
!Output is written in file sr.dat
!Interface to be used with relativistic particles.
!========================================================
program sr_solve
include ’sr.inc’
real(8) :: T0,TF,X10,X20,X30,V10,V20,V30
real(8) :: P10,P20,P30
real(8) :: P1,P2,P3,V1,V2,V3
real(8) :: t,dt,tstep
integer :: STEPS
integer :: i
real(8) :: energy
!Arrays/variables needed by rksuite:
real(8) :: TOL,THRES(NEQ), WORK(LENWRK), Y(NEQ), YMAX(NEQ),&
YP(NEQ), YSTART(NEQ),HSTART
logical :: ERRASS, MESSAGE
integer :: UFLAG
!.. External Subroutines ..
EXTERNAL F, SETUP, STAT, UT
!Input:
print *,’Runge-Kutta Method for 6-ODEs Integration’
print *,’Special Relativistic Particle:’
print *,’Enter coupling constants k1,k2,k3,k4:’
read *, k1,k2,k3,k4
print *,’k1= ’,k1,’ k2= ’,k2,’ k3= ’,k3,’ k4= ’,k4
print *,’Enter STEPS,T0,TF,X10,X20,X30,V10,V20,V30:’
read *, STEPS,T0,TF,X10,X20,X30,V10,V20,V30
call momentum(V10,V20,V30,P10,P20,P30)
print *,’No. Steps= ’,STEPS
print *,’Time: Initial T0 =’,T0,’ Final TF=’,TF
print *,’ X1(T0)=’,X10,’ X2(T0)=’,X20,’ X3(T0)=’,X30
print *,’ V1(T0)=’,V10,’ V2(T0)=’,V20,’ V3(T0)=’,V30
print *,’ P1(T0)=’,P10,’ P2(T0)=’,P20,’ P3(T0)=’,P30
!Initial Conditions
dt = (TF-T0)/STEPS
YSTART(1) = X10
YSTART(2) = X20
YSTART(3) = X30
YSTART(4) = P10
YSTART(5) = P20
YSTART(6) = P30
!
! Set error control parameters.
!
TOL = 5.0D-6
do i = 1, NEQ
THRES(i) = 1.0D-10
enddo
MESSAGE = .TRUE.
ERRASS = .FALSE.
HSTART = 0.0D0
!Initialization:
call SETUP(NEQ,T0,YSTART,TF,TOL,THRES,METHOD,’Usual Task’,&
ERRASS,HSTART,WORK,LENWRK,MESSAGE)
open(unit=11,file=’sr.dat’)
call velocity(YSTART(4),YSTART(5),YSTART(6),V1,V2,V3)
write(11,100) T0,YSTART(1),YSTART(2),YSTART(3),&
V1,V2,V3,&
energy(T0,YSTART),&
YSTART(4),YSTART(5),YSTART(6)
!Calculation:
do i=1,STEPS
t = T0 + i*dt
call UT(F,t,tstep,Y,YP,YMAX,WORK,UFLAG)
if(UFLAG.GT.2) exit
call velocity(Y(4),Y(5),Y(6),V1,V2,V3)
write(11,100) tstep,Y(1),Y(2),Y(3),&
V1,V2,V3,&
energy(tstep,Y),&
Y(4),Y(5),Y(6)
enddo
close(11)
100 format(11E25.15)
end program sr_solve
!========================================================
!momentum -> velocity transformation
!========================================================
subroutine velocity(p1,p2,p3,v1,v2,v3)
implicit none
real(8) :: v1,v2,v3,p1,p2,p3,v,p,vsq,psq
psq = p1*p1+p2*p2+p3*p3
v1 = p1/sqrt(1.0D0+psq)
v2 = p2/sqrt(1.0D0+psq)
v3 = p3/sqrt(1.0D0+psq)
end subroutine velocity
!========================================================
!velocity -> momentum transformation
!========================================================
subroutine momentum(v1,v2,v3,p1,p2,p3)
implicit none
real(8) :: v1,v2,v3,p1,p2,p3,v,p,vsq,psq
vsq = v1*v1+v2*v2+v3*v3
if(vsq .ge. 1.0D0 ) stop ’sub momentum: vsq >= 1’
p1 = v1/sqrt(1.0D0-vsq)
p2 = v2/sqrt(1.0D0-vsq)
p3 = v3/sqrt(1.0D0-vsq)
end subroutine momentum
The subroutines momentum and velocity compute the transformations (6.7) . In
the subroutine momentum we check whether the condition (6.8) is satisfied. These
functions are also used in the subroutine F that computes the derivatives of the
functions.
The test drive of the above program is the well known relativistic motion of a
charged particle in a constant EM field. The acceleration of the particle is
given by equations (6.3) . The relativistic kinetic energy of the particle
is
 | (6.9) |
These relations are programmed in the file sr_B.f90. The contents of the file
sr_B.f90 are:
!========================================================
! Particle in constant Magnetic and electric field
! q B/m = k1 z q E/m = k2 x + k3 y + k4 z
!========================================================
subroutine F(T,Y,YP)
include ’sr.inc’
real(8) :: t
real(8) :: Y(*),YP(*)
real(8) :: x1,x2,x3,v1,v2,v3,p1,p2,p3
x1 = Y(1);p1 = Y(4)
x2 = Y(2);p2 = Y(5)
x3 = Y(3);p3 = Y(6)
call velocity(p1,p2,p3,v1,v2,v3)
!now we can use all x1,x2,x3,p1,p2,p3,v1,v2,v3
YP(1) = v1
YP(2) = v2
YP(3) = v3
!Acceleration:
YP(4) = k2 + k1 * v2
YP(5) = k3 - k1 * v1
YP(6) = k4
end subroutine F
!========================================================
!Energy per unit rest mass
!========================================================
real(8) function energy(T,Y)
include ’sr.inc’
real(8) :: t,e
real(8) :: Y(*)
real(8) :: x1,x2,x3,v1,v2,v3,p1,p2,p3,psq
x1 = Y(1);p1 = Y(4)
x2 = Y(2);p2 = Y(5)
x3 = Y(3);p3 = Y(6)
psq= p1*p1+p2*p2+p3*p3
!Kinetic Energy/m_0
e = sqrt(1.0D0+psq)-1.0D0
!Potential Energy/m_0
e = e - k2*x1 - k3*x2 - k4*x3
energy = e
end function energy
The results are shown in figures 6.5–6.6.
Now we can study a more interesting problem. Consider a simple model of the
Van Allen radiation belt. Assume that the electrons are moving within the
Earth’s magnetic field which is modeled after a magnetic dipole field of the
form:
![( )3 [ ]
B⃗ = B0 RE-- 3 (dˆ⋅ ˆr)ˆr − ˆd ,
r](main_latex2648x.png) | (6.10) |
where  is the magnetic dipole moment of the Earth’s magnetic field and
is the magnetic dipole moment of the Earth’s magnetic field and
 . The parameter values are approximately equal to
. The parameter values are approximately equal to  ,
,
 , where
, where  is the radius of the Earth. The typical energy of
the moving particles is
is the radius of the Earth. The typical energy of
the moving particles is  MeV which corresponds to velocities of
magnitude
MeV which corresponds to velocities of
magnitude  . We choose
the coordinate axes so that
. We choose
the coordinate axes so that  and we measure distance in
and we measure distance in  units .
Then we obtain:
units .
Then we obtain:
The magnetic dipole field is programmed in the file sr_Bd.f90:
!========================================================
! Particle in Magnetic dipole field:
! q B_1/m = k1 (3 x1 x3)/r^5
! q B_2/m = k1 (3 x2 x3)/r^5
! q B_3/m = k1[(3 x3 x3)/r^5-1/r^3]
!========================================================
subroutine F(T,Y,YP)
include ’sr.inc’
real(8) :: t
real(8) :: Y(*),YP(*)
real(8) :: x1,x2,x3,v1,v2,v3,p1,p2,p3
real(8) :: B1,B2,B3
real(8) :: r
x1 = Y(1);p1 = Y(4)
x2 = Y(2);p2 = Y(5)
x3 = Y(3);p3 = Y(6)
call velocity(p1,p2,p3,v1,v2,v3)
!now we can use all x1,x2,x3,p1,p2,p3,v1,v2,v3
YP(1) = v1
YP(2) = v2
YP(3) = v3
!Acceleration:
r = sqrt(x1*x1+x2*x2+x3*x3)
if( r.gt.0.0D0)then
B1 = k1*( 3.0D0*x1*x3)/r**5
B2 = k1*( 3.0D0*x2*x3)/r**5
B3 = k1*((3.0D0*x3*x3)/r**5-1/r**3)
YP(4) = v2*B3-v3*B2
YP(5) = v3*B1-v1*B3
YP(6) = v1*B2-v2*B1
else
YP(4) = 0.0D0
YP(5) = 0.0D0
YP(6) = 0.0D0
endif
end subroutine F
!========================================================
!Energy per unit rest mass
!========================================================
real(8) function energy(T,Y)
include ’sr.inc’
real(8) :: t,e
real(8) :: Y(*)
real(8) :: x1,x2,x3,v1,v2,v3,p1,p2,p3,psq
x1 = Y(1);p1 = Y(4)
x2 = Y(2);p2 = Y(5)
x3 = Y(3);p3 = Y(6)
psq= p1*p1+p2*p2+p3*p3
!Kinetic Energy/m_0
e = sqrt(1.0D0+psq)-1.0D0
energy = e
end function energy
The results are shown in figure 6.8. The parameters have been exaggerated in
order to achieve an aesthetically pleasant result. In reality, the electrons are
moving in very thin spirals and the reader is encouraged to use more realistic
values for the parameters  ,
,  ,
,  . The problem of why the effect is not seen
near the equator is left as an exercise.
. The problem of why the effect is not seen
near the equator is left as an exercise.
6.4 Problems
- Compute the trajectory of a projectile moving in space in a constant
gravitational field and under the influence of an air resistance
proportional to the square of its speed.
- Two point charges are moving with non relativistic speeds in a constant
magnetic field
 . Assume that their interaction is given by the
Coulomb force only. Write a program that computes their trajectory
numerically using the RK45 method.
. Assume that their interaction is given by the
Coulomb force only. Write a program that computes their trajectory
numerically using the RK45 method.
- Write a program that computes the trajectory of the anisotropic
harmonic oscillator


 . Compute the
three dimensional Lissajous curves which appear for appropriate
values of the angular frequencies
. Compute the
three dimensional Lissajous curves which appear for appropriate
values of the angular frequencies  ,
,  ,
,
 .
.
- Two particles of mass
 are at the fixed positions
are at the fixed positions  and
and
 . A third particle of mass
. A third particle of mass  interacts with them via a
Newtonian gravitational force and moves at non relativistic speeds.
Compute the particle’s trajectory and find initial conditions that result
in a planar motion.
interacts with them via a
Newtonian gravitational force and moves at non relativistic speeds.
Compute the particle’s trajectory and find initial conditions that result
in a planar motion.
- Solve problem 5.19 of page 758 using the RK45 method. Choose initial
conditions so that the system executes only translational motion. Next,
choose initial conditions so that the system executes small vibrations
and its center of mass remains stationary. Find the normal modes of the
system and choose appropriate initial conditions that put the system
in each one of them.
- Solve the previous problem by putting the system in a box
 and
and  .
.
Hint: Look in the file springL.f90.
- Solve the problem 5.20 in page 759 by using the RK45 method.
- Solve the problem 5.21 in page 759 by using the RK45 method.
- The electric field of an electric dipole
 is given by: where
is given by: where  ,
,  ,
,  and
and
 are the polar coordinates of the point where the electric field is
calculated. Calculate the trajectory of a test charge moving in this
field at non relativistic speeds. Calculate the deviation between the
relativistic and the non relativistic trajectories when the initial speed is
are the polar coordinates of the point where the electric field is
calculated. Calculate the trajectory of a test charge moving in this
field at non relativistic speeds. Calculate the deviation between the
relativistic and the non relativistic trajectories when the initial speed is
 respectively (ignore radiation effects).
respectively (ignore radiation effects).
- Consider a linear charge distribution with constant linear charge density
 .
The electric field is given by
.
The electric field is given by
 Calculate the trajectories of two equal negative test charges that move at
non relativistic speeds in this field. Consider only the electrostatic Coulomb
forces and ignore anything else.
Calculate the trajectories of two equal negative test charges that move at
non relativistic speeds in this field. Consider only the electrostatic Coulomb
forces and ignore anything else.
- Consider a linear charge distribution on four straight lines parallel to the
 axis. The linear charge density is
axis. The linear charge density is  and it is constant. The four straight
lines intersect the
and it is constant. The four straight
lines intersect the  plane at the points
plane at the points  ,
,  ,
,  ,
,
 . Calculate the trajectory of a non relativistic charge in this
field. Next, compute the relativistic trajectories (ignore all radiation
effects).
. Calculate the trajectory of a non relativistic charge in this
field. Next, compute the relativistic trajectories (ignore all radiation
effects).
- Three particles of mass
 interact via their Newtonian gravitational force.
Compute their (non relativistic) trajectories in space.
interact via their Newtonian gravitational force.
Compute their (non relativistic) trajectories in space.
Chapter 7
Electrostatics
In this chapter we will study the electric field
generated by a static charge distribution. First we will compute the electric field
lines and the equipotential surfaces of the electric field generated by a static point
charge distribution on the plane. Then we will study the electric field generated
by a continuous charge distribution on the plane. This requires the numerical
solution of an elliptic boundary value problem which will be done using successive
over-relaxation (SOR) methods.
7.1 Electrostatic Field of Point Charges
Consider  point charges
point charges  which are located at fixed positions on the plane
given by their position vectors
which are located at fixed positions on the plane
given by their position vectors  ,
,  . The electric field is given by
Coulomb’s law
. The electric field is given by
Coulomb’s law
 | (7.1) |
where  is the unit vector in the direction of
is the unit vector in the direction of  . The
components of the field are
. The
components of the field are
The electrostatic potential at  is
is
 | (7.3) |
and we have that
 | (7.4) |
The electric field lines are the integral curves of the vector field  , i.e. the
curves whose tangent lines at each point are parallel to the electric field at that
point. The magnitude of the electric field is proportional to the density of the field
lines (the number of field lines per perpendicular area). This means that the
electric flux
, i.e. the
curves whose tangent lines at each point are parallel to the electric field at that
point. The magnitude of the electric field is proportional to the density of the field
lines (the number of field lines per perpendicular area). This means that the
electric flux  through a surface
through a surface  is proportional to the number
of field lines that cross the surface. Electric field lines of point charge distributions
start from positive charges (sources), end in negative charges (sinks) or extend to
infinity.
is proportional to the number
of field lines that cross the surface. Electric field lines of point charge distributions
start from positive charges (sources), end in negative charges (sinks) or extend to
infinity.
The equipotential surfaces are the loci of the points of space where the
electrostatic potential takes fixed values. hey are closed surfaces. Equation (7.4)
tells us that a strong electric field at a point is equivalent to a strong spatial variation
of the electric potential at this point, i.e. to dense equipotential surfaces. The
direction of the electric field is perpendicular to the equipotential surfaces at each
point ,
which is the direction of the strongest spatial variation of  , and it
points in the direction of decreasing
, and it
points in the direction of decreasing  . The planar cross sections of the
equipotential surfaces are closed curves which are called equipotential
lines.
. The planar cross sections of the
equipotential surfaces are closed curves which are called equipotential
lines.
The computer cannot solve a problem in the continuum and we have to
consider a finite discretization of a field line. A continuous curve is approximated
by a large but finite number of small line segments. The basic idea is illustrated in
figure 7.1: The small line segment  is taken in the direction of the electric field
and we obtain
is taken in the direction of the electric field
and we obtain
 | (7.5) |
where  .
.
In order to calculate the equipotential lines we use the property that they are
perpendicular to the electric field at each point. Therefore, if  is in the
tangential direction of a field line, then
is in the
tangential direction of a field line, then  is in the perpendicular
direction since
is in the perpendicular
direction since  . Therefore the
equations that give the equipotential lines are
. Therefore the
equations that give the equipotential lines are
 | (7.6) |
The algorithm that will allow us to perform an approximate calculation of the
electric field lines and the equipotential lines is the following: Choose an initial
point that belongs to the (unique) line that you want to draw. The electric field
can be calculated from the known electric charge distribution and equation (7.2) .
By using a small enough step  we move in the direction
we move in the direction  to the new
position
to the new
position
 | (7.7) |
where we use equations (7.5) or (7.6) . The procedure is repeated until the
drawing is finished. The programmer sets a criterion for that, e.g. when the field
line steps out of the drawing area or approaches a charge closer than a minimum
distance.
7.2 The Program – Appetizer and ... Desert
The hurried, but slightly experienced reader may skip the details of this section
and go directly to section 7.4. There she can find the final form of the program
and brief usage instructions.
In order to program the algorithm described in the previous section, we will
separate the algorithmic procedures into four different but well defined tasks:
- Main program: The data structure, which is given by the position of
the charges stored in the arrays X(P), Y(P) and the charges stored
in the array Q(P), is defined. It also contains the user interface which
consists of reading data entered by the user, like the number of charges
N, their positions and magnitude. Then the calculation of a group of
field or equipotential lines is performed by calling the routines eline
or epotline respectively.
- subroutine eline(xin,yin,X,Y,Q,N): Calculates the electric field line
passing through the point xin,yin. On entry, the user inputs the point
xin,yin and the data N, X(N), Y(N), Q(N). On exit, the subroutine
prints to the stdout the coordinates of the approximate electric field
line. The line extends up to a point that is either too close to one of the
point charges or until the line leaves the drawing area .
It calls the subroutines efield for the calculation of the electric field
and mdist for the calculation of the minimum and maximum distance
of a point on the field line from all the point charges.
- subroutine epotline(xin,yin,X,Y,Q,N): Calculates the equipotential
line passing through the point xin,yin. On entry, the user inputs
the point xin,yin and the data N, X(N), Y(N), Q(N). On exit, the
subroutine prints to the stdout the coordinates of the approximate
equipotential line. The subroutine stops calculating an equipotential
line when it comes back close enough to the original point
xin,yin or when it leaves the drawing area. It calls the subroutines
efield for the calculation of the electric field and mdist for the calculation
of the minimum and maximum distance of a point on the equipotential
line from all the point charges.
- subroutine efield(x0,y0,X,Y,Q,N,Ex,Ey): Calculates the electric
field Ex, Ey at position x0, y0. On entry, the user provides the number
of charges N, the position of charges X(N), Y(N), the charges Q(N) and
the position x0, y0. On exit, the routine provides the values Ex, Ey.
- subroutine mdist(x0,y0,X,Y,N,rmin,rmax):
Calculates the maximum and minimum distance of the point x0, y0
from all charges located at X(N), Y(N). On entry, the user provides the
number of charges N, the position of charges X(N), Y(N) and the point
x0, y0. On exit, the routine provides the minimum and maximum
distances rmin,rmax.
In the main program, the variables N, X(N), Y(N) and Q(N) must
be set. These can be hard coded by the programmer or entered by the
user interactively. The first choice is coded in the program listed below,
which can be found in the file ELines.f90. This is version 1 of the main
program:
!****************************************************
program Electric_Fields
!****************************************************
implicit none
integer,parameter :: P=20 !max number of charges
real,dimension(P) :: X,Y,Q
integer :: N
!------------- SET CHARGE DISTRIBUTION ----
N = 2
X(1) = 1.0
Y(1) = 0.0
Q(1) = 1.0
X(2) = -1.0
Y(2) = 0.0
Q(2) = -1.0
!------------- DRAWING LINES -------------
call eline(0.0, 0.5,X,Y,Q,N)
call eline(0.0, 1.0,X,Y,Q,N)
call eline(0.0, 1.5,X,Y,Q,N)
call eline(0.0, 2.0,X,Y,Q,N)
call eline(0.0,-0.5,X,Y,Q,N)
call eline(0.0,-1.0,X,Y,Q,N)
call eline(0.0,-1.5,X,Y,Q,N)
call eline(0.0,-2.0,X,Y,Q,N)
end program Electric_Fields
The commands
!------------- SET CHARGE DISTRIBUTION ----
N = 2
X(1) = 1.0
Y(1) = 0.0
Q(1) = 1.0
X(2) = -1.0
Y(2) = 0.0
Q(2) = -1.0
define two opposite charges Q(1)= -Q(2)= 1.0 located at  and
and  respectively. The next lines call the subroutine eline in order to perform the
calculation of 8 field lines passing through the points
respectively. The next lines call the subroutine eline in order to perform the
calculation of 8 field lines passing through the points  ,
,  ,
,
 ,
,  :
:
!------------- DRAWING LINES -------------
call eline(0.0, 0.5,X,Y,Q,N)
call eline(0.0, 1.0,X,Y,Q,N)
call eline(0.0, 1.5,X,Y,Q,N)
call eline(0.0, 2.0,X,Y,Q,N)
call eline(0.0,-0.5,X,Y,Q,N)
call eline(0.0,-1.0,X,Y,Q,N)
call eline(0.0,-1.5,X,Y,Q,N)
call eline(0.0,-2.0,X,Y,Q,N)
These commands print the coordinates of the field lines to the stdout and the
user can analyze them further.
The program for calculating the equipotential lines is quite similar. The calls
to the subroutine eline are substituted by calls to epotline.
For the program to be complete, we must program the subroutines
eline, efield, mdist. This will be done later, and you can find the
full code in the file ELines.f90. For the moment, let’s copy the main
program
listed above into the file Elines.f90 and compile and run it with the
commands:
> gfortran ELines.f90 -o el
> ./el > el.out
The stdout of the program is redirected to the file el.out. We can plot the
results with gnuplot:
gnuplot> plot "el.out" with dots
The result is shown in figure 7.2.
Let’s modify the program so that the user can enter the charge distribution, as
well as the number and position of the field lines that she wants to draw,
interactively. The part of the code that we need to change is:
!------------- SET CHARGE DISTRIBUTION ----
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
The first line asks the user to enter the number of charges in the distribution.
It proceeds with reading it from the stdin and prints the result to the
stdout. The following loop reads the positions and charges and stores
them at the position i of the arrays X(i), Y(i), Q(i). The results are
printed to the stdout so that the user can check the values read by the
program.
The drawing of the field lines is now done by modifying the code so
that:
!------------- DRAWING LINES -------------
print *,’# How many lines to draw? ’
read *, draw
do i=1,draw
print *,’# Initial point (x0,y0): ’
read *, x0,y0
call eline(x0,y0,X,Y,Q,N)
enddo
As a test case, we run the program for one charge  located at the origin
and we draw one field line passing through the point
located at the origin
and we draw one field line passing through the point  .
.
> gfortran ELines.f90 -o el
> ./el
# Enter number of charges:
1
# N= 1
# Charge: 1
# Position and charge: (X,Y,Q):
0.0 0.0 1.0
# (X,Y)= 0.000000 0.000000 Q= 1.000000
# How many lines to draw?
1
# Initial point (x0,y0):
0.1 0.1
9.2928931E-02 9.2928931E-02
8.5857861E-02 8.5857861E-02
7.8786790E-02 7.8786790E-02
....
For charge distributions with a large number of point charges, use an editor to
record the charges, their positions and the points where the field lines should go
through.
2 N: Number of Charges
1.0 0.0 1.0 (X,Y,Q): Position and charge
-1.0 0.0 -1.0 (X,Y,Q): Position and charge
8 Number of lines to draw
0.0 0.5 x0,y0: Initial point of line
0.0 1.0 x0,y0: Initial point of line
0.0 1.5 x0,y0: Initial point of line
0.0 2.0 x0,y0: Initial point of line
0.0 -0.5 x0,y0: Initial point of line
0.0 -1.0 x0,y0: Initial point of line
0.0 -1.5 x0,y0: Initial point of line
0.0 -2.0 x0,y0: Initial point of line
If the data listed above is written into a file, e.g. Input, then the command
./el < Input > el.out
reads the data from the file Input and redirects the data printed to the stdout
to the file el.out. This way you can create a “library” of charge distributions and
the field lines of their respective electric fields. The complete code (version 2) is
listed below:
!****************************************************
program Electric_Fields
!****************************************************
implicit none
integer,parameter :: P=20 !max number of charges
real,dimension(P) :: X,Y,Q
integer :: N
integer :: i,j,draw
real :: x0,y0
!------------- SET CHARGE DISTRIBUTION ----
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
!------------- DRAWING LINES -------------
print *,’# How many lines to draw? ’
read *, draw
do i=1,draw
print *,’# Initial point (x0,y0): ’
read *, x0,y0
call eline(x0,y0,X,Y,Q,N)
enddo
end program Electric_Fields
If you did the exercises described above, you should have already realized that
in order to draw a nice representative picture of the electric field can be
time consuming. For field lines one can use simple physical intuition in
order to automate the procedure. For distances close enough to a point
charge the electric field is approximately isotropic. The number of field
lines crossing a small enough curve which contains only the charge is
proportional to the charge (Gauss’s law). Therefore we can draw a small
circle centered around each charge and choose initial points isotropically
distributed on the circle as initial points of the field lines. The code listed below
(version 3) implements the idea for charges that are equal in magnitude. For
charges different in magnitude, the program is left as an exercise to the
reader.
!****************************************************
program Electric_Fields
!****************************************************
implicit none
integer,parameter:: P=20 !max number of charges
real,dimension(P):: X,Y,Q
integer :: N
integer :: i,j,nd
real :: x0,y0,theta
real,parameter :: PI= 3.14159265359
!------------- SET CHARGE DISTRIBUTION ----
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
!------------- DRAWING LINES -------------
!We draw 2*nd field lines around each charge
nd = 6
do i = 1,N
do j = 1,(2*nd)
theta = (PI/nd)*j
x0 = X(i) + 0.1 * cos(theta)
y0 = Y(i) + 0.1 * sin(theta)
call eline(x0,y0,X,Y,Q,N)
enddo
enddo
end program Electric_Fields
We set the number of field lines around each charge to be equal to 12 (nd=6). The
initial points are taken on the circle whose center is (X(i),Y(i)) and its radius is
0.1. The 2*nd points are determined by the angle theta=(PI/nd)*j.
We record the data of a charge distribution in a file, e.g. Input. Below, we list
the example of four equal charges  located at the vertices of a
square:
located at the vertices of a
square:
4 N: Number of charges
1 1 -1 (X,Y,Q): Position and charge
-1 1 1 (X,Y,Q): Position and charge
1 -1 1 (X,Y,Q): Position and charge
-1 -1 -1 (X,Y,Q): Position and charge
Then we give the commands:
> gfortran ELines.f90 -o el
> ./el < Input > el.out
> gnuplot
gnuplot> plot "el.out" with dots
The results are shown in figures 7.3 and 7.4. The reader should determine the
charge distributions that generate those fields and reproduce the figures as an
exercise.
For the computation of the equipotential lines we can work in a similar way.
We will follow a quick and dirty way which will not produce an accurate picture of
the electric field and choose the initial points evenly spaced on an square
lattice. For a better choice see problem 5. The listed code is in the file
EPotential.f90:
!****************************************************
program Electric_Potential
!****************************************************
implicit none
integer,parameter :: P=20 !max number of charges
real,dimension(P) :: X,Y,Q
integer :: N
real,parameter :: PI= 3.14159265359
integer :: i,j,nd
real :: x0,y0,rmin,rmax,L
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
!------------- DRAWING LINES -------------
!We draw lines passing through an equally
!spaced lattice of N=(2*nd+1)x(2*nd+1) points
!in the square -L<= x <= L, -L<= y <= L.
nd = 4
L = 1.0
do i = -nd,nd
do j = -nd,nd
x0 = i*(L/nd)
y0 = j*(L/nd)
print *,’# @ ’,i,j,L/nd,x0,y0
call mdist(x0,y0,X,Y,N,rmin,rmax)
!we avoid getting too close to a charge:
if(rmin .gt. L/(nd*10) )&
call epotline(x0,y0,X,Y,Q,N)
enddo
enddo
end program Electric_Potential
The first and second part of the code is identical to the previous one. In the third
part we call the subroutine epotline for drawing an equipotential line for each
initial point. The initial points are on a square lattice with (2*nd+1)*(2*nd+1)=
81 points (nd=4). The lattice extends within the limits set by the square  ,
,
 ,
,  ,
,  (L=1.0). For each point (x0,y0) we calculate the
equipotential line that passes through it. We check that this point is not
too close to one of the charges by calling the subroutine mdist. The call
determines the minimum distance rmin of the point from all the charges which
should be larger than L/(nd*10). You can run the program with the
commands:
(L=1.0). For each point (x0,y0) we calculate the
equipotential line that passes through it. We check that this point is not
too close to one of the charges by calling the subroutine mdist. The call
determines the minimum distance rmin of the point from all the charges which
should be larger than L/(nd*10). You can run the program with the
commands:
> gfortran EPotential.f90 -o ep
> ./ep < Input > ep.out
> gnuplot
gnuplot> plot "ep.out" with dots
Some of the results are shown in figure 7.5.
7.3 The Program – Main Dish
In this section we look under the hood and give the details of the inner parts of
the program: The subroutines eline and epotline that calculate the field and
equipotential lines, the subroutine efield that calculates the electric field at a
point and the subroutine mdist that calculates the minimum and maximum
distances of a point from the point charges.
The subroutine eline is called by the command:
call eline(x0,y0,X,Y,Q,N)
The input to the routine is the initial point (x0,y0), the number of charges N,
the positions of the charges (X(N),Y(N)) and the charges Q(N). The
routine needs some parameters in order to draw the field line. These are
“hard coded”, i.e. set to fixed values by the programmer that cannot
be changed by the user that calls the routine in her program. One of
them is the step  of equation (7.5) which sets the discretization step
of the field line. It also sets the minimum distance of approaching to a
charge equal to
of equation (7.5) which sets the discretization step
of the field line. It also sets the minimum distance of approaching to a
charge equal to  . The size of the drawing area of the curve is set
by the parameter max_dist=20.0. We should also provide a check in
the program that checks whether the electric field is zero, in which case
the result of the calculation in equation (7.5) becomes indeterminate.
By taking
. The size of the drawing area of the curve is set
by the parameter max_dist=20.0. We should also provide a check in
the program that checks whether the electric field is zero, in which case
the result of the calculation in equation (7.5) becomes indeterminate.
By taking  , the motion is in the direction of the electric field,
which ends on a negative charge or outside the drawing area (why?). In
order to draw the line in both directions, set
, the motion is in the direction of the electric field,
which ends on a negative charge or outside the drawing area (why?). In
order to draw the line in both directions, set  and repeat the
calculation.
and repeat the
calculation.
The code is listed below:
!****************************************************
subroutine eline(xin,yin,X,Y,Q,N)
!****************************************************
implicit none
integer :: N
real,dimension(N):: X,Y,Q
real :: xin,yin,x0,y0
real,parameter :: step=0.01
real,parameter :: max_dist=20.0
integer :: i,direction
real :: rmin,rmax,r,dx,dy,dl
real :: Ex,Ey,E
do direction = -1,1,2 !direction= +/- 1
dl = direction * step
x0 = xin
y0 = yin
dx = 0.0
dy = 0.0
call mdist(x0,y0,X,Y,N,rmin,rmax)
do while(rmin .gt. (2.0*step) .and. rmax .lt. max_dist)
print *,x0,y0
! We evaluate the E-field at the midpoint: This reduces
! systematic errors
call efield(x0+0.5*dx,y0+0.5*dy,X,Y,Q,N,Ex,Ey)
E = sqrt(Ex*Ex+Ey*Ey)
if( E .le. 1.0e-10 ) exit
dx = dl*Ex/E
dy = dl*Ey/E
x0 = x0 + dx
y0 = y0 + dy
call mdist(x0,y0,X,Y,N,rmin,rmax)
enddo !do while()
enddo !do direction = -1,1,2
end subroutine eline
In the first part of the code we have the variable declarations. We only note the
declaration
real,dimension(N):: X,Y,Q
which declares the dimension of the arrays to be N instead of their true dimension
P. This is fine, as long as the programmer of the calling program has already
checked that N  P. The necessary memory for the arrays is allocated in the
calling program and the declaration does not provide new storage space. The
arrays X,Y, Q are passed to the subroutine “by reference”, i.e. the routine learns
about their position in the memory to which it can refer to, and not “by value”.
The parameters
P. The necessary memory for the arrays is allocated in the
calling program and the declaration does not provide new storage space. The
arrays X,Y, Q are passed to the subroutine “by reference”, i.e. the routine learns
about their position in the memory to which it can refer to, and not “by value”.
The parameters  step and max_dist are fixed by the parameter
attribute:
step and max_dist are fixed by the parameter
attribute:
real,parameter :: step=0.01
real,parameter :: max_dist=20.0
Their values should be the result of a careful study by the programmer since they
determine the accuracy of the calculation.
The outmost loop
do direction = -1,1,2
dl = direction * step
...
enddo
sets the direction of motion on the field line (i.e. the sign of  ). The
command do direction = -1,1,2 executes the loop twice by setting the
variable direction to take values from
). The
command do direction = -1,1,2 executes the loop twice by setting the
variable direction to take values from  to
to  with step equal to
with step equal to
 .
.
The commands x0 = xin, y0 = yin define the initial point on the field line.
(x0, y0) is the current point on the field line which is printed to the stdout
with the command print. The variables (dx, dy) set the step (x0, y0)
 (x0+dx, y0+dy). The drawing of the field line is done in the inner
loop
(x0+dx, y0+dy). The drawing of the field line is done in the inner
loop
call mdist(x0,y0,X,Y,N,rmin,rmax)
do while(rmin .gt. (2.0*step) .and. rmax .lt. max_dist)
...
call mdist(x0,y0,X,Y,N,rmin,rmax)
enddo
which is executed provided that the logical expression (rmin .gt. (2.0*step) .and.
rmax .lt. max_dist) is .TRUE. This happens as long as the current point is at a
distance greater than 2.0*step and the maximum distance from all charges is less than
max_dist .
The minimum and maximum distances are calculated by calling the subroutine
mdist.
The electric field, needed in equation (7.5) , is calculated by a call to
efield(x0+0.5*dx,y0+0.5*dy,X,Y,Q,N,Ex,Ey). The first two arguments give
the point at which we want to calculate the electric field, which is chosen to be
the midpoint (x0+dx/2,y0+dy/2) instead of (x0,y0). This improves the stability
and the accuracy of the algorithm.
Equation (7.5) is coded in the commands
E = sqrt(Ex*Ex+Ey*Ey)
dx = dl*Ex/E
dy = dl*Ey/E
x0 = x0 + dx
y0 = y0 + dy
We also perform checks for the cases E=0.0 and dx=dy=0.0:
if( E .le. 1.0e-10 ) exit
When the magnitude of the electric field becomes too small we stop the
calculation by exiting the loop with the command exit. The reader can improve
the code by adding more checks of singular cases.
The subroutine epotline is programmed in a similar way. The relevant code is
listed below:
!****************************************************
subroutine epotline(xin,yin,X,Y,Q,N)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y,Q
real :: xin,yin,x0,y0
real,parameter :: step=0.02
real,parameter :: max_dist=20.0
integer :: i
real :: r,dx,dy,dl
real :: Ex,Ey,E
dl = step
x0 = xin
y0 = yin
dx = 0.0
dy = 0.0
r = step !in order to start loop
do while( r .gt. (0.9*dl) .and. r .lt. max_dist)
print *,x0,y0
! We evaluate the E-field at the midpoint: This reduces
! systematic errors
call efield(x0+0.5*dx,y0+0.5*dy,X,Y,Q,N,Ex,Ey)
E = sqrt(Ex*Ex+Ey*Ey)
if( E .le. 1.0e-10 ) exit
dx = dl*Ey/E
dy = -dl*Ex/E
x0 = x0 + dx
y0 = y0 + dy
r = sqrt((x0-xin)**2+(y0-yin)**2)
enddo !do while()
end subroutine epotline
The differences are minor: The equipotential lines are closed curves, therefore we
only need to transverse them in one direction. The criterion for ending the
calculation is to approach the initial point close enough or leave the drawing
area:
do while( r .gt. (0.9*dl) .and. r .lt. max_dist)
...
enddo
The values of dx, dy are calculated according to equation (7.6) :
dx = dl*Ey/E
dy = -dl*Ex/E
The subroutine efield is an application of
equations
(7.2) :
!****************************************************
subroutine efield(x0,y0,X,Y,Q,N,Ex,Ey)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y,Q
real :: x0,y0,dx,dy,Ex,Ey
integer :: i
real :: r3,xi,yi
Ex = 0.0
Ey = 0.0
do i= 1,N
xi = x0-X(i)
yi = y0-Y(i)
r3 = (xi*xi+yi*yi)**(-1.5)
Ex = Ex + Q(i)*xi*r3
Ey = Ey + Q(i)*yi*r3
enddo
end subroutine efield
Finally, the subroutine mdist calculates the minimum and maximum
distance rmin and rmax of a point (x0,y0) from all the point charges in the
distribution:
!****************************************************
subroutine mdist(x0,y0,X,Y,N,rmin,rmax)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y
real :: x0,y0,rmin,rmax
integer :: i
real :: r
rmax = 0.0
rmin = 1000.0
do i = 1,N
r = sqrt((x0-X(i))**2 + (y0-Y(i))**2)
if(r.GT.rmax) rmax = r
if(r.LT.rmin) rmin = r
enddo
end subroutine mdist
The initial value of rmin depends of the limits of the drawing area (why?).
7.4 The Program - Conclusion
In this section we list the programs discussed in the previous sections and provide
short usage information for compiling, running and analyzing your results.
You can jump into this section without reading the previous ones and go
back to them if you need to clarify some points that you find hard to
understand.
First we list the contents of the file ELines.f90:
!****************************************************
program Electric_Fields
!****************************************************
implicit none
integer,parameter:: P=20 !max number of charges
real,dimension(P):: X,Y,Q
integer :: N
integer :: i,j,nd
real :: x0,y0,theta
real,parameter :: PI= 3.14159265359
!------------- SET CHARGE DISTRIBUTION ----
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
!------------- DRAWING LINES -------------
!We draw 2*nd field lines around each charge
nd = 6
do i = 1,N
do j = 1,(2*nd)
theta = (PI/nd)*j
x0 = X(i) + 0.1 * cos(theta)
y0 = Y(i) + 0.1 * sin(theta)
call eline(x0,y0,X,Y,Q,N)
enddo
enddo
end program Electric_Fields
!****************************************************
subroutine eline(xin,yin,X,Y,Q,N)
!****************************************************
implicit none
integer :: N
real,dimension(N):: X,Y,Q
real :: xin,yin,x0,y0
real,parameter :: step=0.01
real,parameter :: max_dist=20.0
integer :: i,direction
real :: rmin,rmax,r,dx,dy,dl
real :: Ex,Ey,E
do direction = -1,1,2 !direction= +/- 1
dl = direction * step
x0 = xin
y0 = yin
dx = 0.0
dy = 0.0
call mdist(x0,y0,X,Y,N,rmin,rmax)
do while(rmin .gt. (2.0*step) .and. rmax .lt. max_dist)
print *,x0,y0
! We evaluate the E-field at the midpoint: This reduces
! systematic errors
call efield(x0+0.5*dx,y0+0.5*dy,X,Y,Q,N,Ex,Ey)
E = sqrt(Ex*Ex+Ey*Ey)
if( E .le. 1.0e-10 ) exit
dx = dl*Ex/E
dy = dl*Ey/E
x0 = x0 + dx
y0 = y0 + dy
call mdist(x0,y0,X,Y,N,rmin,rmax)
enddo !do while()
enddo !do direction = -1,1,2
end subroutine eline
!****************************************************
subroutine efield(x0,y0,X,Y,Q,N,Ex,Ey)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y,Q
real :: x0,y0,dx,dy,Ex,Ey
integer :: i
real :: r3,xi,yi
Ex = 0.0
Ey = 0.0
do i= 1,N
xi = x0-X(i)
yi = y0-Y(i)
! Exercise: Improve code so that xi*xi+yi*yi=0 is taken care of
r3 = (xi*xi+yi*yi)**(-1.5)
Ex = Ex + Q(i)*xi*r3
Ey = Ey + Q(i)*yi*r3
enddo
end subroutine efield
!****************************************************
subroutine mdist(x0,y0,X,Y,N,rmin,rmax)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y
real :: x0,y0,rmin,rmax
integer :: i
real :: r
rmax = 0.0
rmin = 1000.0
do i = 1,N
r = sqrt((x0-X(i))**2 + (y0-Y(i))**2)
if(r.GT.rmax) rmax = r
if(r.LT.rmin) rmin = r
enddo
end subroutine mdist
Then we list the contents of the file EPotential.f90:
!****************************************************
program Electric_Potential
!****************************************************
implicit none
integer,parameter :: P=20 !max number of charges
real,dimension(P) :: X,Y,Q
integer :: N
real,parameter :: PI= 3.14159265359
integer :: i,j,nd
real :: x0,y0,rmin,rmax,L
print *, ’# Enter number of charges:’
read *, N
print *, ’# N= ’,N
do i=1,N
print *,’# Charge: ’,i
print *,’# Position and charge: (X,Y,Q):’
read *, X(i),Y(i),Q(i)
print *,’# (X,Y)= ’, X(i),Y(i), ’ Q= ’,Q(i)
enddo
!------------- DRAWING LINES -------------
!We draw lines passing through an equally
!spaced lattice of N=(2*nd+1)x(2*nd+1) points
!in the square -L<= x <= L, -L<= y <= L.
nd = 4
L = 1.0
do i = -nd,nd
do j = -nd,nd
x0 = i*(L/nd)
y0 = j*(L/nd)
print *,’# @ ’,i,j,L/nd,x0,y0
call mdist(x0,y0,X,Y,N,rmin,rmax)
!we avoid getting too close to a charge:
if(rmin .gt. L/(nd*10) )&
call epotline(x0,y0,X,Y,Q,N)
enddo
enddo
end program Electric_Potential
!****************************************************
subroutine epotline(xin,yin,X,Y,Q,N)
!****************************************************
implicit none
integer :: N
real,dimension(N) :: X,Y,Q
real :: xin,yin,x0,y0
real,parameter :: step=0.02
real,parameter :: max_dist=20.0
integer :: i
real :: r,dx,dy,dl
real :: Ex,Ey,E
dl = step
x0 = xin
y0 = yin
dx = 0.0
dy = 0.0
r = step !in order to start loop
do while( r .gt. (0.9*dl) .and. r .lt. max_dist)
print *,x0,y0
! We evaluate the E-field at the midpoint: This reduces
! systematic errors
call efield(x0+0.5*dx,y0+0.5*dy,X,Y,Q,N,Ex,Ey)
E = sqrt(Ex*Ex+Ey*Ey)
if( E .le. 1.0e-10 ) exit
dx = dl*Ey/E
dy = -dl*Ex/E
x0 = x0 + dx
y0 = y0 + dy
r = sqrt((x0-xin)**2+(y0-yin)**2)
enddo !do while()
end subroutine epotline
...
where ... are the subroutines efield and mdist which are identical to the ones
in the file ELines.f90.
In order to compile the program use the commands:
> gfortran ELines.f90 -o el
> gfortran EPotential.f90 -o ep
Then, edit a file and name it e.g. Input and write the data that define a charge
distribution. For example:
4 N: Number of charges
1 1 -1 (X,Y,Q): Position and charge
-1 1 1 (X,Y,Q): Position and charge
1 -1 1 (X,Y,Q): Position and charge
-1 -1 -1 (X,Y,Q): Position and charge
The results are obtained with the commands:
> ./el < Input > el.dat
> ./ep < Input > ep.dat
> gnuplot
gnuplot> plot "el.dat" with dots
gnuplot> plot "ep.dat" with dots
Have fun!
7.5 Electrostatic Field in the Vacuum
Consider a time independent electric field in an area of space which is
empty of electric charge. Maxwell’s equations are reduced to Gauss’s
law
 | (7.8) |
together with the equation that defines the electrostatic
potential
Equations (7.8) and (7.9) give the Laplace equation for the function
 :
:
 | (7.10) |
The solution of the equation above is a boundary value problem: We are
looking for the potential  in a region of space
in a region of space  bounded by a closed
surface
bounded by a closed
surface  . When the potential is known on
. When the potential is known on  the solution to (7.10) is
unique and the potential and the electric field is determined everywhere in
the solution to (7.10) is
unique and the potential and the electric field is determined everywhere in
 .
.
For simplicity consider the problem confined on a plane, therefore
 . In this case the last term in equation (7.10) vanishes, the region
. In this case the last term in equation (7.10) vanishes, the region
 is a compact subset of the plane and
is a compact subset of the plane and  is a closed curve.
is a closed curve.
For the numerical solution of the problem, we approximate  by a discrete,
square lattice. The potential is defined on the
by a discrete,
square lattice. The potential is defined on the  sites of the lattice. We
take
sites of the lattice. We
take  to be bounded by a square with sides of length
to be bounded by a square with sides of length  . The distance
between the nearest lattice points is called the lattice constant
. The distance
between the nearest lattice points is called the lattice constant  . Then
. Then
 , where
, where  is the number of lattice points on each side of
the square. The continuous solution is approximated by the solution on
the lattice, and the approximation becomes exact in the
is the number of lattice points on each side of
the square. The continuous solution is approximated by the solution on
the lattice, and the approximation becomes exact in the  and
and
 limits, so that the length
limits, so that the length  remains constant. The
curve
remains constant. The
curve  is approximated by the lattice sites that are located on the
perimeter of the square and the loci in the square where the potential takes
constant values. This is a simple model of a set of conducting surfaces
(points where
is approximated by the lattice sites that are located on the
perimeter of the square and the loci in the square where the potential takes
constant values. This is a simple model of a set of conducting surfaces
(points where  const.
const.  ) in a compact region whose boundary is
grounded (points where
) in a compact region whose boundary is
grounded (points where  ). An example is depicted in figure 7.6.
). An example is depicted in figure 7.6.
In order to derive a finite difference equation which approximates equation
(7.10) , we Taylor expand around a point  according to the equations:
according to the equations:
By summing both sides of the above equations, taking  and ignoring the
terms implied by
and ignoring the
terms implied by  , we obtain The second term in the second line was eliminated by using equation (7.10)
.
, we obtain The second term in the second line was eliminated by using equation (7.10)
.
We map the coordinates of the lattice points to integers  such that
such that
 and
and  where
where  . By taking
. By taking  so that
so that 


 and
and 


 , equation (7.11) becomes:
, equation (7.11) becomes:
 | (7.12) |
The equation above states that the potential at the position  is the
arithmetic mean of the potential of the nearest neighbors. We will describe an
algorithm which belongs to the class of “successive overrelaxation methods”
(SOR) whose basic steps are:
is the
arithmetic mean of the potential of the nearest neighbors. We will describe an
algorithm which belongs to the class of “successive overrelaxation methods”
(SOR) whose basic steps are:
- Set the size
 of the square lattice.
of the square lattice.
- Flag the sites that correspond to “conductors”, i.e. the sites where the
potential remains fixed to the boundary conditions values.
- Choose an initial trial function for
 on the vacuum sites. Of
course it is not the solution we are looking for. A good choice will lead
to fast convergence of the algorithm to the true solution. A bad choice
may lead to slow convergence, no convergence or even convergence to
the wrong solution. In our case the problem is easy and the simple
choice
on the vacuum sites. Of
course it is not the solution we are looking for. A good choice will lead
to fast convergence of the algorithm to the true solution. A bad choice
may lead to slow convergence, no convergence or even convergence to
the wrong solution. In our case the problem is easy and the simple
choice  will do.
will do.
- Sweep the lattice and enforce equation (7.12) on each visited vacuum
site. This defines the new value of the potential at this site.
- Sweep the lattice repeatedly until two successive sweeps result in a very
small change in the function
 .
.
A careful study of the above algorithm requires to test different criteria of “very small
change” and test that different choices of the initial function  result in
the same solution.
result in
the same solution.
We write a program that implements this algorithm in the case of a system
which is the projection of two parallel conducting planes inside a grounded cubic
box on the plane. The lattice is depicted in figure 7.6, where the black dots
correspond to the conductors. All the points of the box have  and the
two conductors are at constant potential
and the
two conductors are at constant potential  and
and  respectively. The
user enters the values
respectively. The
user enters the values  and
and  , the lattice size
, the lattice size  and the required
accuracy interactively. The latter is determined by a small number
and the required
accuracy interactively. The latter is determined by a small number  . The
convergence criterion that we set is that the maximum difference between the
values of the potential between two successive sweeps should be less than
. The
convergence criterion that we set is that the maximum difference between the
values of the potential between two successive sweeps should be less than
 .
.
The data structure is very simple. We use a real array V(L,L) in order to store
the values of the potential at each lattice site. A logical array isConductor(L,L)
flags each site as a “conductor site” (= .TRUE.) or as a “vacuum site”
(=.FALSE.).
The main program reads in the data entered by the user and then calls three
subroutines:
- initialize_lattice(V,isConductor,L,V1,V2):
The routine needs at its input the values of the potential V1 and V2 on
the left and right plate respectively and the size of the lattice L. On
exit it provides the initial values of the potential V(L,L) and the flags
isConductor(L,L). The geometry of the setting is hard coded and the
user needs to change this subroutine each time that she wants to study
a different geometry.
- laplace(V,isConductor,L,epsilon):
This is the heart of the program. On entry we provide the initialized
arrays V(L,L) and isConductor(L,L), the lattice size L, and the desired
accuracy epsilon. On exit we obtain the final solution V(L,L). This
subroutine calculates the arithmetic mean of the potential of the nearest
neighbors Vav and the value V(i,j)=Vav is changed immediately .
The maximum change in the new value of the potential Vav from the
old one V(i,j) is stored in the variable error. When error becomes
smaller than epsilon we assume that convergence has been achieved.
- print_results(V,L):
This subroutine prints the potential V(L,L) to the file data. Each line
contains the integers i, j and the value of the potential V(i,j). We
note that each time that the index i changes, the subroutine prints an
extra empty line. This is done so that the output can be read easily by
the three dimensional plotting function splot of gnuplot.
The full program is listed below:
!*************************************************************
!PROGRAM LAPLACE_EM
!Computes the electrostatic potential around conductors.
!The computation is performed on a square lattice of linear
!dimension L. A relaxation method is used to converge to the
!solution of Laplace equation for the potential.
!DATA STRUCTURE:
!real(8) V(L,L): Value of the potential on the lattice sites
!logical isConductor(L,L): If .TRUE. site has fixed potential
! If .FALSE. site is empty space
!real epsilon: Determines the accuracy of the solution
!The maximum difference of the potential on each site between
!two consecutive sweeps should be less than epsilon.
!PROGRAM STRUCTURE
!main program:
! . Data Input
! . call subroutines for initialization, computation and
! printing of results
!subroutine initialize_lattice:
! . Initilization of V(L,L) and isConductor(L,L)
!subroutine laplace:
! . Solves laplace equation using a relaxation method
!subroutine print_results:
! . Prints results for V(L,L) in a file. Uses format compatible
!with splot of gnuplot.
!*************************************************************
program laplace_em
implicit none
!P defines the size of the arrays and is equal to L
integer,parameter :: P=31
logical,dimension(P,P) :: isConductor
real(8),dimension(P,P) :: V
!V1 and V2 are the values of the potential on the interior
!conductors. epsilon is the accuracy desired for the
!convergence of the relaxation method in subroutine
!laplace()
real(8) :: V1,V2,epsilon
integer :: L
!We ask the user to provide the necessary data:
!V1,V2 and epsilon
L = P
print *,’Enter V1,V2:’
read *, V1,V2
print *,’Enter epsilon:’
read *, epsilon
print *,’Starting Laplace:’
print *,’Grid Size= ’,L
print *,’Conductors set at V1= ’,V1,’ V2= ’,V2
print *,’Relaxing with accuracy epsilon= ’,epsilon
!The arrays V and isConductor are initialized
call initialize_lattice(V,isConductor,L,V1,V2)
!We enter initialized V,isConductor. On exit the
!routine gives the solution V
call laplace(V,isConductor,L,epsilon)
!We print V in a file.
call print_results(V,L)
end program laplace_em
!*************************************************************
!subroutine initialize_lattice
!Initializes arrays V(L,L) and isConductor(L,L).
!V(L,L)= 0.0 and isConductor(L,L)= .FALSE. by default
!isConductor(i,j)= .TRUE. on boundary of lattice where V=0
!isConductor(i,j)= .TRUE. on sites with i= L/3+1, 5<= j <= L-5
!isConductor(i,j)= .TRUE. on sites with i=2*L/3+1, 5<= j <= L-5
!V(i,j) = V1 on all sites with i= L/3+1, 5<= j <= L-5
!V(i,j) = V2 on all sites with i=2*L/3+1, 5<= j <= L-5
!V(i,j) = 0 on boundary (i=1,L and j=1,L)
!V(i,j) = 0 on interior sites with isConductor(i,j)= .FALSE.
!INPUT:
!integer L: Linear size of lattice
!real(8) V1,V2: Values of potential on interior conductors
!OUTPUT:
!real(8) V(L,L): Array provided by user. Values of potential
!logical isConductor(L,L): If .TRUE. site has fixed potential
! If .FALSE. site is empty space
!*************************************************************
subroutine initialize_lattice(V,isConductor,L,V1,V2)
implicit none
integer :: L
logical,dimension(L,L) :: isConductor
real(8),dimension(L,L) :: V
real(8) :: V1,V2
integer :: i,j
!Initialize to 0 and .FALSE (default values for boundary and
!interior sites).
V = 0.0D0
isConductor = .FALSE.
!We set the boundary to be a conductor: (V=0 by default)
do i=1,L
isConductor(1,i) = .TRUE.
isConductor(i,1) = .TRUE.
isConductor(L,i) = .TRUE.
isConductor(i,L) = .TRUE.
enddo
!We set two conductors at given potential V1 and V2
do i=5,L-5
V ( L/3+1,i) = V1
isConductor( L/3+1,i) = .TRUE.
V (2*L/3+1,i) = V2
isConductor(2*L/3+1,i) = .TRUE.
enddo
end subroutine initialize_lattice
!*************************************************************
!subroutine laplace
!Uses a relaxation method to compute the solution of the
!Laplace equation for the electrostatic potential
!on a 2 dimensionalsquarelattice of linear size L.
!At every sweep of the lattice we compute the average
!Vav of thepotential at each site (i,j) and we immediately
! update V(i,j).
!The computation continues until Max |Vav-V(i,j)| < epsilon
!INPUT:
!integer L: Linear size of lattice
!real(8) V(L,L): Value of the potential at each site
!logical isConductor(L,L): If .TRUE. potential is fixed
! If .FALSE. potential is updated
!real(8) epsilon: if Max |Vav-V(i,j)| < epsilon return to
!callingprogram.
!OUTPUT:
!real(8) V(L,L): The computed solution for the potential
!*************************************************************
subroutine laplace(V,isConductor,L,epsilon)
implicit none
integer :: L
logical,dimension(L,L) :: isConductor
real(8),dimension(L,L) :: V
real(8) :: epsilon
integer :: i,j,icount
real(8) :: Vav,error,dV
icount = 0 !counts number of sweeps
do while (.TRUE.) !an infinite loop:
error = 0.0D0 !Exit when error<epsilon
do j=2,L-1
do i=2,L-1
!We change V only for non conductors:
if( .NOT. isConductor(i,j))then
Vav = ( V(i-1,j)+V(i+1,j)+V(i,j+1)+V(i,j-1)) * 0.25D0
dV = DABS(V(i,j)-Vav)
if(error .LT. dV ) error = dV !maximum error
V(i,j) = Vav ! we immendiately update V(i,j)
endif
enddo
enddo
icount = icount + 1
print *,icount,’ err= ’,error
if( error .LT. epsilon) return !return to main program
enddo
end subroutine laplace
!*************************************************************
!subroutine print_results
!Prints the array V(L,L) in file "data"
!The format of the output is appropriate for the splot function
!of gnuplot: Each time i changes an empty line is printed.
!INPUT:
!integer L: size of array V
!real(8) V(L,L): array to be printed
!OUTPUT:
!no output
!*************************************************************
subroutine print_results(V,L)
implicit none
integer :: L
real(8),dimension(L,L) :: V
integer :: i,j
open(unit=11,file="data")
do i=1,L
do j =1,L
write(11,*)i,j,V(i,j)
enddo
write (11,*)’’ !empty line for gnuplot,separate isolines
enddo
end subroutine print_results
7.6 Results
The program in the previous section is written in the file LaplaceEq.f90.
Compiling and running is done with the commands:
> gfortran LaplaceEq.f90 -o lf
> ./lf
Enter V1,V2:
100 -100
Enter epsilon:
0.01
Starting Laplace:
Grid Size= 31
Conductors set at V1= 100. V2= -100.
Relaxing with accuracy epsilon= 0.01
1 err= 33.3333333
2 err= 14.8148148
3 err= 9.87654321
.......................
110 err= 0.0106860904
111 err= 0.0101182476
112 err= 0.00958048937
In the example above, the program performs 112 sweeps until the error becomes
0.00958048937 < 0.01. The results are stored in the file data. We can
make a three dimensional plot of the function  with the gnuplot
commands:
with the gnuplot
commands:
gnuplot> set pm3d
gnuplot> set hidden3d
gnuplot> set size ratio 1
gnuplot> splot "data" with lines
The results are shown in figure 7.7
7.7 Poisson Equation
This section contains a short discussion of the case where the space is filled
with a continuous static charge distribution given by the charge density
function  . In this case the Laplace equation becomes the Poisson
equation:
. In this case the Laplace equation becomes the Poisson
equation:
 | (7.13) |
The equation on the lattice becomes
 | (7.14) |
where
 .
.
The program in the file PoissonEq.f90 solves equation (7.14) for
a uniform charge distribution (figure 7.10), where we have set  .
The reader is asked to reproduce this figure together with figures 7.8 and
7.9.
.
The reader is asked to reproduce this figure together with figures 7.8 and
7.9.
!*************************************************************
!set the boundary of a square to given potentials
!*************************************************************
program poisson_eq
implicit none
integer,parameter :: P=51
logical,dimension(P,P) :: isConductor
real(8),dimension(P,P) :: V,rho
real(8) :: V1,V2,V3,V4,Q,epsilon
integer :: L
L = P
print *,’Enter V1,V2,V3,V4:’
read *, V1,V2,V3,V4
print *,’Enter 4*PI*Q:’
read *, Q
print *,’Enter epsilon:’
read *, epsilon
print *,’Starting Laplace:’
print *,’Grid Size= ’,L
print *,’Boundaries set at V1= ’,V1,’ V2= ’,V2,’ V3= ’,V3,&
’ V4= ’,V4,’ and Q= ’,Q
print *,’Relaxing with accuracy epsilon= ’,epsilon
call initialize_lattice(V,isConductor,rho,L,V1,V2,V3,V4,Q)
call laplace(V,isConductor,rho,L,epsilon)
call print_results(V,L)
end program laplace_sq
!**********************************************************
subroutine &
initialize_lattice(V,isConductor,rho,L,V1,V2,V3,V4,Q)
!**********************************************************
implicit none
integer :: L
logical,dimension(L,L) :: isConductor
real(8),dimension(L,L) :: V,rho
real(8) :: V1,V2,V3,V4,Q,Area
integer :: i,j,L1,L2
!Initialize to 0 and .FALSE.
V = 0.0D0
isConductor = .FALSE.
rho = 0.0D0
!We set the boundary to be a conductor:
do i=1,L
isConductor(1,i) = .TRUE.
isConductor(i,1) = .TRUE.
isConductor(L,i) = .TRUE.
isConductor(i,L) = .TRUE.
V (1,i) = V1
V (i,L) = V2
V (L,i) = V3
V (i,1) = V4
enddo
!We set the points with non-zero charge
!A uniform distribution at a center square
L1 = (L/2)-5
L2 = (L/2)+5
if(L1.LT.1) stop ’array rho out of bounds. Small L1’
if(L2.GT.L) stop ’array rho out of bounds. Large L2’
Area = (L2-L1+1)*(L2-L1+1)
do j=L1,L2
do i=L1,L2
rho(i,j) = Q/Area !rho is \tilde\rho in notes
enddo !so Q is 4*PI*Q
enddo
end subroutine initialize_lattice
!*************************************************************
subroutine laplace(V,isConductor,rho,L,epsilon)
!*************************************************************
implicit none
integer :: L
logical,dimension(L,L) :: isConductor
real(8),dimension(L,L) :: V,rho
real(8) :: epsilon
integer :: i,j,icount
real(8) :: Vav,error,dV
icount = 0
do while (.TRUE.)
error = 0.0D0
do j=2,L-1
do i=2,L-1
!We change the voltage only for non conductors:
if( .NOT. isConductor(i,j))then
Vav = (V(i-1,j)+V(i+1,j)+V(i,j+1)+V(i,j-1)+rho(i,j))&
*0.25D0
dV = DABS(V(i,j)-Vav)
if(error .LT. dV ) error = dV !maximum error
V(i,j) = Vav
endif
enddo
enddo
icount = icount + 1
if( error .LT. epsilon) exit
enddo
print *,icount,’ err= ’,error
end subroutine laplace
!*************************************************************
subroutine print_results(V,L)
!*************************************************************
implicit none
integer :: L
real(8),dimension(L,L) :: V
integer :: i,j
open(unit=11,file="data")
do i=1,L
do j =1,L
write(11,*)i,j,V(i,j)
enddo
write (11,*)’’ !empty line for gnuplot,separate isolines
enddo
end subroutine print_results
In the bibliography the algorithm described above is called the Gauss–Seidel
method. In this method, the right hand side of equation (7.14) uses the updated
values of the potential in the calculation of  and
and  is immediately
updated. In contrast, the Jacobi method uses the old values of the potential in the
right hand side of (7.14) and the new value computed is stored in order
to be used in the next sweep. The Gauss–Seidel method is superior to
the Jacobi method as far as speed of convergence is concerned. We can
generalize Jacobi’s method by defining the residual
is immediately
updated. In contrast, the Jacobi method uses the old values of the potential in the
right hand side of (7.14) and the new value computed is stored in order
to be used in the next sweep. The Gauss–Seidel method is superior to
the Jacobi method as far as speed of convergence is concerned. We can
generalize Jacobi’s method by defining the residual  of equation
(7.14)
of equation
(7.14)
 | (7.15) |
which vanishes when  is a solution of equation (7.14) . Then, using
is a solution of equation (7.14) . Then, using  ,
Jacobi’s method can be formulated as
,
Jacobi’s method can be formulated as
 | (7.16) |
where the quantities with index  refer to the values of the potential during
the
refer to the values of the potential during
the  -th sweep. The successive overrelaxation (SOR) method is given
by:
-th sweep. The successive overrelaxation (SOR) method is given
by:
 | (7.17) |
When  we have “underrelaxation” and we obtain slower convergence than
the Jacobi method. When
we have “underrelaxation” and we obtain slower convergence than
the Jacobi method. When  we have “overrelaxation” and an
appropriate choice of
we have “overrelaxation” and an
appropriate choice of  can lead to an improvement compared to the Jacobi
method. When
can lead to an improvement compared to the Jacobi
method. When  SOR diverges. Further study of the SOR methods is left as
an exercise to the reader.
SOR diverges. Further study of the SOR methods is left as
an exercise to the reader.
7.8 Problems
- Reproduce the figures with the electric field lines and equipotential
lines shown in section 7.2.
- Take the charge distributions that you used in the previous problems,
make all the charges to be positive and remake the figures of the field
lines and the equipotential lines. Then repeat by taking half of the
charges to be twice in magnitude than the others.
- The program ELines.f90 gets stuck when you apply it on a charge
distribution of four equal charges located at the vertices of a square.
How can you correct this pathology?
- Make the necessary changes to the program in the file ELines.f90 so
that the number of field lines starting near a charge
 is proportional
to
is proportional
to  .
.
- Improve the program in EPotential.f90 so that the equipotential lines are
drawn with a density proportional to the magnitude of the electric
field.
Hint:
- Write a subroutine that calculates the potential
 at the
point
at the
point  .
.
- From each point charge draw a line in the radial direction and
calculate the potential on points that are at small distance
 from each other.
from each other.
- Calculate the maximum/minimum value of the potential
 /
/ and use them in order to choose the values
of the potential on the equipotential lines that you plan to
draw. If e.g. you choose to draw 5 equipotential lines, take
and use them in order to choose the values
of the potential on the equipotential lines that you plan to
draw. If e.g. you choose to draw 5 equipotential lines, take
 and
and 
 .
.
- Repeat the second step. When the potential at a point takes
approximately one of the values
 chosen in the previous step,
draw an equipotential line from that point.
chosen in the previous step,
draw an equipotential line from that point.
- Compute the electric potential using the program in the file LaplaceEq.f90
for
- L= 31, V1=100, V2=100
- L= 31, V1=100, V2=0
and construct the corresponding plot for  .
.
- Compute the electric potential using the program in the file LaplaceEq.f90
for
- V1=100, V2=100
- V1=100, V2=100
- V1=100, V2=0
for L=31,61,121,241,501 and construct the corresponding plot for
 . Vary epsilon=0.1, 0.01, 0.001, 0.0001, 0.00001,
0.000001. What is the dependence of the number of sweeps
. Vary epsilon=0.1, 0.01, 0.001, 0.0001, 0.00001,
0.000001. What is the dependence of the number of sweeps  on
epsilon? Make the plot of
on
epsilon? Make the plot of  (epsilon). Put the points and curves of
(epsilon). Put the points and curves of
 (epsilon) for all values of L on the same plot.
(epsilon) for all values of L on the same plot.
- Compute the electrostatic potential of a square conductor when the
potential on each side is V1, V2, V3, V4. Repeat what you did in the
previous problem for
- V1=10, V2=5, V3=10, V4= 5
- V1=10, V2=0, V3=0, V4= -10
- V1=10, V2=0, V3=0, V4= 0
- Compute the electrostatic potential of a system of square conductors where
the one is inside the other as shown in figure 7.11. The side of each
conductor has L1, L2 sites respectively and the value of the potential
is V1,V2 respectively. Take L2= L1/5 and repeat the steps in the
previous problem for V1=10, V2=-10 and L1= 25, 50, 100, 200.
- Perform a numerical computation of the capacitance
 of the
system of conductors of the previous problem when
of the
system of conductors of the previous problem when  ,
,  . In
order to calculate the charge
. In
order to calculate the charge  , compute the surface charge density
, compute the surface charge density  using the equation
using the equation
 where
where  is the perpendicular component of the electric field on the
surface. Use the approximation
is the perpendicular component of the electric field on the
surface. Use the approximation
 where
where  is the potential difference between a point on the conductor and
its nearest neighbor. By integrating (i.e. summing) you can estimate the
total charge on each conductor. If these are opposite and their absolute
value is
is the potential difference between a point on the conductor and
its nearest neighbor. By integrating (i.e. summing) you can estimate the
total charge on each conductor. If these are opposite and their absolute
value is  , then the capacitance can be calculated from the equation
, then the capacitance can be calculated from the equation
 . Perform the calculation described above for
. Perform the calculation described above for  and
L1=25, 75.
and
L1=25, 75.
- In the system of the previous problem compute the function
 . Verify
that the capacitance is independent of
. Verify
that the capacitance is independent of  . Use L1=25,50, V1= -V2 =1, 2,
5, 10, 15, 20, 25.
. Use L1=25,50, V1= -V2 =1, 2,
5, 10, 15, 20, 25.
- Reproduce figures 7.8, 7.9 and 7.10. Compare the result of the first case with
the known solution of a point charge in empty space.
- Introduce the lattice spacing
 in the corresponding equations in the
program in the file PoissonEq.f90. Set the length of each side to be
in the corresponding equations in the
program in the file PoissonEq.f90. Set the length of each side to be  and print the results in the file data as
and print the results in the file data as  instead of
instead of
 . Take L=51,101,151,201,251 and plot
. Take L=51,101,151,201,251 and plot  in the square
in the square
 ,
,  . Study the convergence of the solutions by plotting
the section
. Study the convergence of the solutions by plotting
the section  for each L.
for each L.
- Write a program that implements the SOR algorithm given by equation
(7.16) for the problem solved in LaplaceEq.f90. Compare the speed
of convergence of SOR with that of the Gauss-Seidel method for
 ,
,  ,
,  ,
,  ,
, 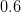 ,
,  ,
,  . What happens when
. What happens when
 ?
?
- Write a program that implements the SOR algorithm given by equation
(7.16) for the problem solved in PoissonEq.f90. Compare the speed
of convergence of SOR with that of the Gauss-Seidel method for
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . What happens when
. What happens when
 ?
?
Chapter 8
Diffusion Equation
8.1 Introduction
The diffusion equation is related to the study of random walks. Consider a
particle moving on a line (one dimension) performing a random walk. The motion
is stochastic and the kernel
 | (8.1) |
is interpreted as the probability density to observe the particle at position  at
time
at
time  if the particle is at
if the particle is at  at
at  . The equation that determines
. The equation that determines
 is
is
 | (8.2) |
which is the diffusion equation. The coefficient  depends on the
details of the system that is studied. For example, for the Brownian
motion of a dust particle in a fluid which moves under the influence of
random collisions with the fluid particles, we have that
depends on the
details of the system that is studied. For example, for the Brownian
motion of a dust particle in a fluid which moves under the influence of
random collisions with the fluid particles, we have that  ,
where
,
where  is the (absolute) temperature of the fluid,
is the (absolute) temperature of the fluid,  is the friction
coefficient
of the particle in the fluid and
is the friction
coefficient
of the particle in the fluid and  is the Boltzmann constant.
is the Boltzmann constant.
Usually the initial conditions are chosen so that at  the particle is localized at one
point
the particle is localized at one
point  , i.e.
, i.e.
 | (8.3) |
The interpretation of  as a probability density implies that for every
as a probability density implies that for every  we
should have that
we
should have that
 | (8.4) |
It is not obvious that this relation can be imposed for every instant of time. Even
if  is normalized so that (8.4) holds for
is normalized so that (8.4) holds for  , the time evolution of
, the time evolution of
 is governed by equation (8.2) which can spoil equation (8.4) at
later times.
is governed by equation (8.2) which can spoil equation (8.4) at
later times.
If we impose equation (8.4) at  , then it will hold at all times
if
, then it will hold at all times
if
 | (8.5) |
By taking into account that 
 and that
and that

 we obtain
we obtain
The above equation tells us that for functions for which the right hand side
vanishes, the normalization condition will be valid for all  .
.
A careful analysis of equation (8.2) gives that the asymptotic behavior of
 for small times is
for small times is
 | (8.7) |
This relation shows that diffusion is isotropic (the same in all directions) and that the
probability of detecting the particle drops exponentially with the distance squared
from the initial position of the particle. This relation cannot hold for all times, since
for large enough times the probability of detecting the particle will be the same
everywhere .
The return probability of the particle to its initial position is
 | (8.8) |
The above relation defines the spectral dimension  of space.
of space.  in our
case.
in our
case.
The expectation value of the distance squared of the particle at time  is easily
calculated
is easily
calculated
 | (8.9) |
This equation is very important. It tells us that the random walk (Brownian
motion) is not a classical motion but it can only be given a stochastic description:
A classical particle moving with constant velocity  so that
so that  results
in
results
in  .
.
In the following sections we take
 and define
and define
 | (8.10) |
8.2 Heat Conduction in a Thin Rod
Consider a thin rod of length  and let
and let  be the temperature distribution
within the rod at time
be the temperature distribution
within the rod at time  . The two ends of the rod are kept at constant
temperature
. The two ends of the rod are kept at constant
temperature  . If the initial temperature distribution in the
rod is
. If the initial temperature distribution in the
rod is  , then the temperature distribution at all times is determined by
the diffusion equation
, then the temperature distribution at all times is determined by
the diffusion equation
 | (8.11) |
where  is the thermal diffusivity,
is the thermal diffusivity,  is the thermal conductivity,
is the thermal conductivity,  is the density and
is the density and  is the specific heat of the rod.
is the specific heat of the rod.
Define
 | (8.12) |
where ![x ∈ [0, 1]](main_latex2964x.png) . The function
. The function  , giving the fraction of the temperature
difference to the temperature at the ends of the rod, is dimensionless
and
, giving the fraction of the temperature
difference to the temperature at the ends of the rod, is dimensionless
and
 | (8.13) |
These are called Dirichlet boundary
conditions .
Equation (8.11) becomes
 | (8.14) |
Equation (8.6) becomes
 | (8.15) |
The relation above cannot be equal to zero at all times due to the boundary
conditions (8.13) . This can be easily understood with an example. Suppose
that
 | (8.16) |
then it is easy to confirm that the boundary conditions are satisfied and that the
function
 | (8.17) |
is the solution to the diffusion equation. It is easy to see that
 drops exponentially with time and that
drops exponentially with time and that
 which is in agreement with equations (8.15) .
which is in agreement with equations (8.15) .
The exponential drop of the magnitude of  is in agreement with the
expectation that the rod will have constant temperature at long times, which will
be equal to the temperature at its ends (
is in agreement with the
expectation that the rod will have constant temperature at long times, which will
be equal to the temperature at its ends ( ).
).
8.3 Discretization
The numerical solution of equation (8.14) will be computed in the interval
![x ∈ [0,1]](main_latex2976x.png) for
for ![t ∈ [0,tf]](main_latex2977x.png) . The problem will be defined on a two dimensional
discrete lattice and the differential equation will be approximated by finite
difference equations.
. The problem will be defined on a two dimensional
discrete lattice and the differential equation will be approximated by finite
difference equations.
The lattice is defined by  spatial points
spatial points ![xi ∈ [0, 1]](main_latex2979x.png)
 | (8.18) |
where the  intervals have the same width
intervals have the same width
 | (8.19) |
and by the  time points
time points ![tj ∈ [0,tf]](main_latex2984x.png)
 | (8.20) |
where the  time intervals have the same duration
time intervals have the same duration
 | (8.21) |
We note that the ends of the intervals correspond to
 | (8.22) |
The function  is approximated by its values on the
is approximated by its values on the  lattice
lattice
 | (8.23) |
The derivatives are replaced by the finite differences
 | (8.24) |
By equating both sides of the above relations according to (8.14) , we obtain the
dynamic evolution of  in time
in time
 | (8.26) |
This is a one step iterative relation in time. This is very convenient, because
one does not need to store the values  for all
for all  in the computer
memory.
in the computer
memory.
The second term (the “second derivative”) in (8.26) contains only the nearest
neighbors  of the lattice point
of the lattice point  at a given time slice
at a given time slice  . Therefore it
can be used for all
. Therefore it
can be used for all  . The relations (8.26) are not needed for
the points
. The relations (8.26) are not needed for
the points  and
and  since the values
since the values 
 are kept
constant.
are kept
constant.
The parameter
 | (8.27) |
determines the time evolution in the algorithm. It is called the Courant parameter
and in order to have a time evolution without instabilities it is necessary to
have
 | (8.28) |
This condition will be checked in our analysis empirically.
8.4 The Program
The fact that equation (8.26) is a one time step iterative relation, leads to a
substantial simplification of the structure of the program. Because of
this, at each time step, it is sufficient to store the values of the second
term (the “second derivative”) in one array. This array will be used in
order to update the values of  . Therefore we will define only two
arrays
. Therefore we will define only two
arrays  ,
,  and
and  ,
,  which store
the values of
which store
the values of  and
and  at time
at time  respectively. In the program listed below, the names of these arrays are u(P) and
d2udx2(P).
respectively. In the program listed below, the names of these arrays are u(P) and
d2udx2(P).
The data is stored in the array positions u(1) ... u(Nx) and d2udx2(1) ...
d2udx2(Nx) and the parameter P is taken large enough so that Nx is always
smaller than P.
The user enters the  Nx,
Nx,  Nt and
Nt and  tf interactively. The
values of
tf interactively. The
values of  ,
,  and
and  courant are calculated during the
initialization.
courant are calculated during the
initialization.
On exit, we obtain the results in the file d.dat which contains  in
three columns. When a time slice is printed, the program prints an empty line so
that the output is easily read by the three dimensional plotting function splot of
gnuplot.
in
three columns. When a time slice is printed, the program prints an empty line so
that the output is easily read by the three dimensional plotting function splot of
gnuplot.
The program is in the file diffusion.f90 and is listed below:
!=======================================================
! 1-dimensional Diffusion Equation with simple
! Dirichlet boundary conditions u(0,t)=u(1,t)=0
! 0<= x <= 1 and 0<= t <= tf
!
! We set initial condition u(x,t=0) that satisfies
! the given boundary conditions.
! Nx is the number of points in spatial lattice:
! x = 0 + (j-1)*dx, j=1,...,Nx and dx = (1-0)/(Nx-1)
! Nt is the number of points in temporal lattice:
! t = 0 + (j-1)*dt, j=1,...,Nt and dt = (tf-0)/(Nt-1)
!
! u(x,0) = sin(pi*x) tested against analytical solution
! u(x,t) = sin(pi*x)*exp(-pi*pi*t)
!
!=======================================================
program diffusion_1d
implicit none
integer,parameter :: P =100000 ! Max no of points
real(8),parameter :: PI=3.1415926535897932D0
real(8),dimension(P) :: u, d2udx2
real(8) :: t,x,dx,dt,tf,courant
integer Nx,Nt,i,j
! --- Input:
print *, ’# Enter: Nx, Nt, tf: (P= ’,P,’ Nx must be < P)’
read *, Nx,Nt,tf
if(Nx .ge. P) stop ’Nx >= P’
if(Nx .le. 3) stop ’Nx <= 3’
if(Nt .le. 2) stop ’Nt <= 2’
! --- Initialize:
dx = 1.0D0/(Nx-1)
dt = tf /(Nt-1)
courant = dt/dx**2
print * ,’# 1d Diffusion Equation: 0<=x<=1, 0<=t<=tf’
print * ,’# dx= ’,dx,’ dt= ’,dt,’ tf= ’, tf
print * ,’# Nx= ’,Nx,’ Nt= ’,Nt
print * ,’# Courant Number= ’,courant
if(courant .gt. 0.5D0) print *,’# WARNING: courant > 0.5’
open(unit=11,file=’d.dat’) ! data file
! --- Initial condition at t=0 ------------------------------
!u(x,0) = sin( pi x)
do i= 1, Nx
x = (i-1)*dx
u(i) = sin(PI*x)
enddo
u(1) = 0.0d0
u(Nx) = 0.0d0
do i= 1,Nx
x = (i-1)*dx
write(11,*) 0.0D0, x, u(i)
enddo
write(11,*)’ ’
! ----------------------------------------------------------
! --- Calculate time evolution:
do j=2,Nt
t = (j-1)*dt
! ----- second derivative:
do i=2,Nx-1
d2udx2(i) = courant*(u(i+1)-2.0D0*u(i)+u(i-1))
enddo
! ----- update:
do i=2,Nx-1
u(i) = u(i) + d2udx2(i)
enddo
do i=1,Nx
x = (i-1)*dx
write(11,*) t, x, u(i)
enddo
write(11,*)’ ’
enddo ! do j=2,Nt
close(11)
end program diffusion_1d
8.5 Results
The compilation and running of the program can be done with the commands:
> gfortran diffusion.f90 -o d
> echo "10 100 0.4" | ./d
# Enter: Nx, Nt, tf: (P= 100000 Nx must be < P)
# 1d Diffusion Equation: 0<=x<=1, 0<=t<=tf
# dx= 0.11111111111111110 dt= 4.04040404040404040E-3 tf= 0.4
# Nx= 10 Nt= 100
# Courant Number= 0.32727272727272733
The input to the program ./d is read from the stdin and it is given by the
stdout of the command echo through a pipe, as shown in the second line in the
listing above. The lines that follow are the standard output stdout of the
program.
The three dimensional plot of the function  can be made with the
gnuplot commands:
can be made with the
gnuplot commands:
gnuplot> set pm3d
gnuplot> set hidden3d
gnuplot> splot "d.dat" with lines
gnuplot> unset pm3d
In order to make the plot of  for a fixed value of
for a fixed value of  we first note that an
empty line in the file d.dat marks a change in time. The following awk program
counts the empty lines of d.dat and prints only the lines when the number of
empty lines that have been encountered so far is equal to 3. The counter n=0, 1,
..., Nt-1 determines the value of
we first note that an
empty line in the file d.dat marks a change in time. The following awk program
counts the empty lines of d.dat and prints only the lines when the number of
empty lines that have been encountered so far is equal to 3. The counter n=0, 1,
..., Nt-1 determines the value of  . We save the results in the file
tj which can be plotted with gnuplot. We repeat as many times as we
wish:
. We save the results in the file
tj which can be plotted with gnuplot. We repeat as many times as we
wish:
> awk ’NF<3{n++}n==3 {print}’ d.dat > tj
gnuplot> plot "tj" using 2:3 with lines
The above task can be completed without creating the intermediate file tj by
using the awk filter within gnuplot. For example, the commands
gnuplot> ! echo "10 800 2" | ./d
gnuplot> plot "<awk ’NF<3{n++}n==3 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==6 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==10 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==20 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==30 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==50 {print}’ d.dat" u 2:3 w l
gnuplot> replot "<awk ’NF<3{n++}n==100{print}’ d.dat" u 2:3 w l
run the program for Nx=10, Nt=800, tf= 2 and construct the plot in figure 8.2
It is instructive to compare the results with the known solution
 . We compute the relative error
. We compute the relative error
 which can be done within gnuplot with the commands:
which can be done within gnuplot with the commands:
gnuplot> du(x,y,z) = (z - sin(pi*x)*exp(-pi*pi*y))/z
gnuplot> plot "<awk ’NF<3{n++}n==2 ’ d.dat" u 2:(du($2,$1,$3))
gnuplot> plot "<awk ’NF<3{n++}n==6 ’ d.dat" u 2:(du($2,$1,$3))
gnuplot> plot "<awk ’NF<3{n++}n==20 ’ d.dat" u 2:(du($2,$1,$3))
gnuplot> plot "<awk ’NF<3{n++}n==200’ d.dat" u 2:(du($2,$1,$3))
gnuplot> plot "<awk ’NF<3{n++}n==600’ d.dat" u 2:(du($2,$1,$3))
gnuplot> plot "<awk ’NF<3{n++}n==780’ d.dat" u 2:(du($2,$1,$3))
The results can be seen in figure 8.3.
8.6 Diffusion on the Circle
In order to study the kernel  for the diffusion, or random walk,
problem, we should impose the normalization condition (8.4) for all times.
In the case of the function
for the diffusion, or random walk,
problem, we should impose the normalization condition (8.4) for all times.
In the case of the function  defined for
defined for ![x ∈ [0, 1]](main_latex3040x.png) the relation
becomes
the relation
becomes
 | (8.29) |
In order to maintain this relation at all times, it is necessary that the right hand
side of equation (8.15) is equal to 0. One way to impose this condition is to
study the diffusion problem on the circle. If we parametrize the circle using the
variable ![x ∈ [0,1 ]](main_latex3042x.png) , then the points
, then the points  and
and  are identified and we
obtain
are identified and we
obtain
 | (8.30) |
The second relation in the above equations makes the right hand side of equation
(8.15) to vanish. Therefore if  , we obtain
, we obtain  ,
,
 .
.
Using the above assumptions, the discretization of the differential equation is
done exactly as in the problem of heat conduction. Instead of keeping
the values  , we apply equation (8.26) also for the
points
, we apply equation (8.26) also for the
points  ,
,  . In order to take into account the cyclic topology we
take
. In order to take into account the cyclic topology we
take
 | (8.31) |
and
 | (8.32) |
since the neighbor to the right of the point  is the point
is the point  and the
neighbor to the left of the point
and the
neighbor to the left of the point  is the point
is the point  . For the rest of the points
. For the rest of the points
 equation (8.26) is applied normally.
equation (8.26) is applied normally.
The program that implements the problem described above can be found in
the file diffusionS1.f90. The boundary conditions (8.30) are enforced in the
lines
nnr = i+1
if(nnr .gt. Nx) nnr = 1
nnl = i-1
if(nnl .lt. 1 ) nnl = Nx
d2udx2(i) = courant*(u(nnr)-2.0D0*u(i)+u(nnl))
The initial conditions at  are chosen so that the particle is located at
are chosen so that the particle is located at
 . For each instant of time we perform measurements in order to verify
the equations (8.4) and (8.9) and the fact that
. For each instant of time we perform measurements in order to verify
the equations (8.4) and (8.9) and the fact that  const.
const.
The variable prob  and we should check that its value is
conserved and is always equal to 1.
and we should check that its value is
conserved and is always equal to 1.
The variable r2  is a discrete estimator of
the expectation value of the distance squared from the initial position.
For small enough times it should follow the law given by equation (8.9)
.
is a discrete estimator of
the expectation value of the distance squared from the initial position.
For small enough times it should follow the law given by equation (8.9)
.
These variables are written to the file e.dat together with the values  ,
,
 and
and  . The latter are measured in order to check if for large enough
times they obtain the same constant value according to the expectation
. The latter are measured in order to check if for large enough
times they obtain the same constant value according to the expectation
 const.
const.
The full code is listed below:
!=======================================================
! 1-dimensional Diffusion Equation with
! periodic boundary conditions u(0,t)=u(1,t)
! 0<= x <= 1 and 0<= t <= tf
!
! We set initial condition u(x,t=0) that satisfies
! the given boundary conditions.
! Nx is the number of points in spatial lattice:
! x = 0 + (j-1)*dx, j=1,...,Nx and dx = (1-0)/(Nx-1)
! Nt is the number of points in temporal lattice:
! t = 0 + (j-1)*dt, j=1,...,Nt and dt = (tf-0)/(Nt-1)
!
! u(x,0) = \delta_{x,0.5}
!
!=======================================================
program diffusion_1d
implicit none
integer,parameter :: P =100000 ! Max no of points
real(8),parameter :: PI=3.1415926535897932D0
real(8),dimension(P) :: u, d2udx2
real(8) :: t,x,dx,dt,tf,courant,prob,r2,x0
integer Nx,Nt,i,j,nnl,nnr
! --- Input:
print *, ’# Enter: Nx, Nt, tf: (P= ’,P,’ Nx must be < P)’
read *, Nx,Nt,tf
if(Nx .ge. P) stop ’Nx >= P’
if(Nx .le. 3) stop ’Nx <= 3’
if(Nt .le. 2) stop ’Nt <= 2’
! --- Initialize:
dx = 1.0D0/(Nx-1)
dt = tf /(Nt-1)
courant = dt/dx**2
print * ,’# 1d Diffusion Equation on S1: 0<=x<=1, 0<=t<=tf’
print * ,’# dx= ’,dx,’ dt= ’,dt,’ tf= ’, tf
print * ,’# Nx= ’,Nx,’ Nt= ’,Nt
print * ,’# Courant Number= ’,courant
if(courant .gt. 0.5D0) print *,’# WARNING: courant > 0.5’
open(unit=11,file=’d.dat’) ! data file
open(unit=12,file=’e.dat’) ! data file
! --- Initial condition at t=0 ------------------------------
do i= 1, Nx
x = (i-1)*dx
u(i) = 0.0D0
enddo
u(Nx/2) = 1.0D0
do i= 1,Nx
x = (i-1)*dx
write(11,*) 0.0D0, x, u(i)
enddo
write(11,*)’ ’
! ----------------------------------------------------------
! --- Calculate time evolution:
do j=2,Nt
t = (j-1)*dt
! ----- second derivative:
do i=1,Nx
nnr = i+1
if(nnr .gt. Nx) nnr = 1
nnl = i-1
if(nnl .lt. 1 ) nnl = Nx
d2udx2(i) = courant*(u(nnr)-2.0D0*u(i)+u(nnl))
enddo
! ----- update:
prob = 0.0D0
r2 = 0.0D0
x0 = ((Nx/2)-1)*dx !original position
do i=1,Nx
x = (i-1)*dx
u(i) = u(i) + d2udx2(i)
prob = prob + u(i)
r2 = r2 + u(i)*(x-x0)*(x-x0)
enddo
do i=1,Nx
x = (i-1)*dx
write(11,*) t, x, u(i)
enddo
write(11,*)’ ’
write(12,*) ’pu ’,t, prob,r2,u(Nx/2),u(Nx/4),u(1)
enddo ! do j=2,Nt
close(11)
end program diffusion_1d
8.7 Analysis
For each moment of time, the program writes the following quantities to the file
e.dat:
 | (8.33) |
which is an estimator of (8.29) and we expect to obtain  for all
for all
 ,
,
 | (8.34) |
which is an estimator of (8.9) for which we expect to obtain
 | (8.35) |
for small times as well as the values of  ,
,  ,
,  .
.
The values of  ,
,  ,
,  ,
,  ,
,  ,
,  are found in
columns 2, 3, 4, 5, 6 and 7 respectively of the file e.dat. The gnuplot
commands
are found in
columns 2, 3, 4, 5, 6 and 7 respectively of the file e.dat. The gnuplot
commands
gnuplot> ! gfortran diffusionS1.f90 -o d
gnuplot> ! echo "10 100 0.4" | ./d
compile and run the program within gnuplot. They set  ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
The gnuplot commands
gnuplot> plot "e.dat" u 2:5 w l
gnuplot> replot "e.dat" u 2:6 w l
gnuplot> replot "e.dat" u 2:7 w l
construct the plot in figure 8.4. We observe that for large times we obtain
uniform diffusion.
The relation  can be easily confirmed by inspecting the values recorded
in the file e.dat.
can be easily confirmed by inspecting the values recorded
in the file e.dat.
The asymptotic relation  can be confirmed with the commands
can be confirmed with the commands
gnuplot> plot [:][:0.11] "e.dat" u 2:4,2*x
which construct the plot in figure 8.5.
Finally we make a plot of the function  with the commands
with the commands
gnuplot> ! echo "10 100 0.16" | ./d
gnuplot> set pm3d
gnuplot> splot [0:0.16][0:1][0: 1] "d.dat" w l
gnuplot> splot [0:0.16][0:1][0:.2] "d.dat" w l
and the result is shown in figure 8.6.
8.8 Problems
- Reproduce the results in figure 8.3.
- The temperature distribution
 in a thin rod satisfies equation
(8.14) together with the boundary conditions (8.13) at the ends
in a thin rod satisfies equation
(8.14) together with the boundary conditions (8.13) at the ends
 . The initial temperature distribution at
. The initial temperature distribution at  is given by
the function
is given by
the function
![{ 0.5 x ∈ [x ,x ]
u(x,0) = 1 2 ,
0.3 x ∕∈ [x1,x2 ]](main_latex3115x.png) where
where  and
and  .
.
- Calculate the temperature distribution
 for
for  ,
,
 ,
,  ,
,  . Take
. Take  and
and  . Do the
same for
. Do the
same for  by choosing appropriate
by choosing appropriate  and keeping
and keeping
 . Plot the functions
. Plot the functions  in the same plot.
in the same plot.
- Calculate the maximum value of the temperature graphically
for
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Take
. Take
 and choose an appropriate value for the corresponding
and choose an appropriate value for the corresponding
 .
.
- Calculate the time at which the temperature of the rod becomes
everywhere less than
 .
.
Hint: Make your program print only the final temperature distribution
 .
.
- The temperature distribution
 in a thin rod satisfies the
equation
in a thin rod satisfies the
equation
 The temperature at the ends of the rod is
The temperature at the ends of the rod is  , and when
, and when

![( [ (2πx)]
{ 0.5 1 − cos -b- 0 ≤ x < b
u(x,0) = 0 b ≤ x ≤ 1 .
(](main_latex3144x.png)
- Calculate the temperature distribution
 for
for  ,
,
 and for
and for 
 ,
,  ,
,  , by taking
, by taking
 ,
,  . Do the same for
. Do the same for  by choosing
appropriate
by choosing
appropriate  . Plot the functions
. Plot the functions  in the same plot.
in the same plot.
- Using the same parameters, calculate the time evolution of the
values of the temperature distribution at the points
 ,
,
 and
and  for
for  . Plot the functions
. Plot the functions
 in the same plot.
in the same plot.
- Calculate the temperature distribution
 for
for  and
and
 for
for  . Plot the functions
. Plot the functions  in the
same plot. Comment on the effect of the parameter
in the
same plot. Comment on the effect of the parameter  on your
results.
on your
results.
- The temperature distribution
 in a thin rod of length
in a thin rod of length  satisfies
equation
satisfies
equation
 where
where  is the
is the  -dependent thermal diffusivity. The
temperature of the rod at its ends is such that
-dependent thermal diffusivity. The
temperature of the rod at its ends is such that  , and at
time
, and at
time  , the temperature distribution is
, the temperature distribution is

- Write a program where the user enters the parameters
 ,
,  ,
,
 ,
,  ,
,  ,
,  and
and  interactively. On exit, the program
calculates
interactively. On exit, the program
calculates  and writes the points
and writes the points  in two
columns to a file d.dat.
in two
columns to a file d.dat.
- Run the program for
 ,
,  ,
,  ,
,  ,
,  ,
,  and calculate
and calculate  for
for  . Plot the functions
. Plot the functions
 in the same plot.
in the same plot.
- Using the same parameters, calculate the time evolution of the
temperature distribution at the points
 and
and  for
for
 . Plot the functions
. Plot the functions  in the same plot.
in the same plot.
- Reproduce the results shown in figures 8.4 and 8.5.
Chapter 9
The Anharmonic Oscillator
In this chapter we will use matrix
methods in order to compute the quantum mechanical energy spectrum of the
anharmonic oscillator. This problem cannot be solved exactly and one has to
resort to perturbative or other approximation methods. We will approach
this problem numerically by representing the Hamiltonian  as a real
symmetric matrix in an appropriately chosen basis of the Hilbert space
as a real
symmetric matrix in an appropriately chosen basis of the Hilbert space  of
quantum mechanical states. The energy spectrum is obtained from the
eigenvalues of this matrix and the numerical problem reduces to that of
the diagonalization of a real symmetric matrix. Since the Hamiltonian is
represented in
of
quantum mechanical states. The energy spectrum is obtained from the
eigenvalues of this matrix and the numerical problem reduces to that of
the diagonalization of a real symmetric matrix. Since the Hamiltonian is
represented in  by an infinite size matrix, we have to restrict ourselves to a
finite dimensional subspace
by an infinite size matrix, we have to restrict ourselves to a
finite dimensional subspace  of dimension
of dimension  . In this space the
Hamiltonian is represented by an
. In this space the
Hamiltonian is represented by an  real symmetric matrix. The
eigenvalues of this matrix will be calculated numerically using standard
methods and the energy eigenvalues will be obtained in the
real symmetric matrix. The
eigenvalues of this matrix will be calculated numerically using standard
methods and the energy eigenvalues will be obtained in the  limit.
limit.
For the calculation of the eigenvalues we will use software that is found in the
well known library Lapack which contains high quality, freely available,
linear algebra software. Part of the goals of this chapter is to show to
the reader how to link her programs with software libraries. In order to
solve the same problem using Mathematica or Matlab see [40] and [41]
respectively.
9.1 Introduction
The Hamiltonian of the harmonic oscillator is given by
 | (9.1) |
Define the position and momentum scales  ,
,  so that
we can express the above equation using dimensionless terms:
so that
we can express the above equation using dimensionless terms:
 | (9.2) |
If we take the units of energy, distance and momentum to be  ,
,  and
and  ,
then we obtain
,
then we obtain
 | (9.3) |
where  ,
,  and
and  are now dimensionless. The operator
are now dimensionless. The operator  can be
diagonalized with the help of the creation and annihilation operators
can be
diagonalized with the help of the creation and annihilation operators  and
and  ,
defined by the relations:
,
defined by the relations:
 | (9.4) |
or
 | (9.5) |
which obey the commutation relation
![[a, a†] = 1,](main_latex3221x.png) | (9.6) |
which leads to
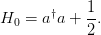 | (9.7) |
The eigenstates  ,
,  of
of  span the Hilbert space of states
span the Hilbert space of states  and satisfy the relations
and satisfy the relations
 | (9.8) |
therefore
 | (9.9) |
and
 | (9.10) |
The position representation of the eigenstates  is given by the wavefunctions:
is given by the wavefunctions:
 | (9.11) |
where  are the Hermite polynomials.
are the Hermite polynomials.
From equations (9.4) and (9.8) we obtain
From the above equations we can easily calculate the Hamiltonian of the
anharmonic oscillator
 | (9.15) |
The matrix elements of  in this representation are:
in this representation are:
where  can be calculated from equation (9.12) :
can be calculated from equation (9.12) :
 | (9.18) |
This relation computes the matrix elements of the matrix  from the matrix
product of
from the matrix
product of  with itself.
with itself.
The problem of the calculation of the energy spectrum has now been reduced
to the problem of calculating the eigenvalues of the matrix  .
.
9.2 Calculation of the Eigenvalues of 
We start by choosing the dimension  of the subspace
of the subspace  of the Hilbert space
of states
of the Hilbert space
of states  . We will restrict ourselves to states within this subspace and we will
use the
. We will restrict ourselves to states within this subspace and we will
use the  dimensional representation matrices of
dimensional representation matrices of  ,
,  and
and  in
in  .
For example, when
.
For example, when  we obtain
we obtain
 | (9.19) |
 | (9.20) |
 | (9.21) |
Our goal is to write a program that calculates the eigenvalues  of
the
of
the  matrix
matrix  . Instead of reinventing the wheel, we will use ready
made routines that calculate eigenvalues and eigenvectors of matrices found in the
Lapack library. This library can be found in the high quality numerical software
repository Netlib and more specifically at http://www.netlib.org/lapack/.
Documentation can be found at http://www.netlib.org/lapack/lug/, but it
is also easily accessible online by a Google search or by using the man
pages .
. Instead of reinventing the wheel, we will use ready
made routines that calculate eigenvalues and eigenvectors of matrices found in the
Lapack library. This library can be found in the high quality numerical software
repository Netlib and more specifically at http://www.netlib.org/lapack/.
Documentation can be found at http://www.netlib.org/lapack/lug/, but it
is also easily accessible online by a Google search or by using the man
pages .
As inexperienced users we will first look for driver routines that perform a
diagonalization process. Since our task is to diagonalize a real symmetric matrix,
we pick the subroutine DSYEV (D = double precision, SY = symmetric, EV =
eigenvalues with optional eigenvectors). If the documentation of the library is
installed in our system, we may use the Linux man pages for accessing
it:
> man dsyev
From this page we learn how to use this subroutine:
SUBROUTINE DSYEV( JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, INFO )
CHARACTER JOBZ, UPLO
INTEGER INFO, LDA, LWORK, N
DOUBLE PRECISION A( LDA, * ),W( * ), WORK( * )
ARGUMENTS
JOBZ (input) CHARACTER*1
= ’N’: Compute eigenvalues only;
= ’V’: Compute eigenvalues and eigenvectors.
UPLO (input) CHARACTER*1
= ’U’: Upper triangle of A is stored;
= ’L’: Lower triangle of A is stored.
N (input) INTEGER
The order of the matrix A. N >= 0.
A (input/output) DOUBLE PRECISION array, dimension (LDA, N)
On entry, the symmetric matrix A. If UPLO = ’U’, the
leading N-by-N upper triangular part of A contains the
upper triangular part of the matrix A. If UPLO = ’L’,
the leading N-by-N lower triangular part of A contains
the lower triangular part of the matrix A. On exit, if
JOBZ = ’V’, then if INFO = 0, A contains
the orthonormal eigenvectors of the matrix A. If
JOBZ = ’N’, then on exit the lower triangle (if UPLO=’L’)
or the upper triangle (if UPLO=’U’) of A, including the
diagonal, is destroyed.
LDA (input) INTEGER
The leading dimension of the array A. LDA >= max(1,N).
W (output) DOUBLE PRECISION array, dimension (N)
If INFO = 0, the eigenvalues in ascending order.
WORK (workspace/output) DOUBLE PRECISION array, dimension
(LWORK).
On exit, if INFO = 0, WORK(1) returns the optimal LWORK.
LWORK (input) INTEGER
The length of the array WORK. LWORK >= max(1,3*N-1).
For optimal efficiency, LWORK >= (NB+2)*N, where NB is
the blocksize for DSYTRD returned by ILAENV.
If LWORK = -1, then a workspace query is assumed; the
routine only calculates the optimal size of the WORK
array, returns this value as the first entry of the
WORK array, and no error message related to LWORK is
issued by XERBLA.
INFO (output) INTEGER
= 0: successful exit
< 0: if INFO = -i, the i-th argument had an illegal value
> 0: if INFO = i, the algorithm failed to converge; i
off-diagonal elements of an intermediate tridiagonal
form did not converge to zero.
These originally cryptic pages contain all the necessary information and
the reader should familiarize herself with its format. For a quick and
dirty use of the routine, all we need to know is the types and usage of its
arguments. These are classified as “input”, “output” and “working space”
variables (some are in more than one classes). Input is the necessary data
that the routine needs in order to perform the computation. Output is
where the results of the computation are stored. And working space is the
memory provided by the user to the routine in order to store intermediate
results.
From the information above we learn that the matrix to be diagonalized is A
which is a rectangular matrix with the number of its rows and columns  .
The number of rows LDA (LDA= “leading dimension of A”) can be larger than
N is which case DSYEV will diagonalize the upper left N
.
The number of rows LDA (LDA= “leading dimension of A”) can be larger than
N is which case DSYEV will diagonalize the upper left N N part of the
matrix .
In our program we define a large matrix A(LDA,LDA) and diagonalize a smaller
submatrix A(N,N). This way we can study many values of
N part of the
matrix .
In our program we define a large matrix A(LDA,LDA) and diagonalize a smaller
submatrix A(N,N). This way we can study many values of  using the same
matrix. The subroutine can be used in two ways:
using the same
matrix. The subroutine can be used in two ways:
- If JOBZ=’N’, it calculates only the eigenvalues of the matrix A(N,N)
and stores them in the array W(N), sorted in ascending order. We
have to be careful because, upon return, the routine destroys the
upper (UPLO=’U’) or lower (UPLO=’L’) triangular part of A. Since A is
symmetric, only this part is needed by DSYEV. If we need to reuse the
matrix A, we have to make a backup copy before the call to DSYEV.
- If JOBZ=’V’, it calculates both the eigenvalues and the eigenvectors of
the matrix A(N,N). The eigenvalues are stored in the array W(N) as
before, whereas the corresponding eigenvectors in the columns of the
matrix A(N,N). In order to use the eigenvectors, we can use a statement
like v = A(1:N,j) where the array v(N) stores the components of the
j-th eigenvector of the matrix corresponding to the eigenvalue
 . The
eigenvectors are normalized to unity, i.e.
. The
eigenvectors are normalized to unity, i.e.  v(i)*v(i)
v(i)*v(i) . The
matrix A(N,N) is destroyed after the call to DSYEV and if we need it we
have to make a backup copy before the call.
. The
matrix A(N,N) is destroyed after the call to DSYEV and if we need it we
have to make a backup copy before the call.
The reader should also familiarize herself with the use of the workspace array WORK.
This is memory space given to the routine for all its intermediate calculations.
Determining the size of this array needs some care. This is given by LWORK
and if performance is an issue the reader should read the documentation
carefully for its optimal determination. We will make the simple choice
LWORK=3*LDA-1. The variable INFO is used as a flag which informs the user
whether the calculation was successful, in which case its value is set to 0.
In our case, if INFO takes a non zero value, the program will abort the
calculation.
Before using the program in a complicated calculation, it is necessary to test
its use in a simple, easily controlled problem. We will familiarize ourselves with
the use of DSYEV by writing the following program:
program test_evs
implicit none
integer, parameter :: P = 100 ! P= LDA
integer, parameter :: LWORK = 3*P-1
real(8) :: A(P,P),W(P),WORK(LWORK)
integer :: N ! DSYEV diagonalizes A(N,N)
integer :: i,j
integer :: LDA,INFO
character(1) :: JOBZ,UPLO
!Define the **symmetric** matrix to be diagonalized
!The subroutine uses the upper triangular part (UPLO=’U’)
!therefore the lower triangular part needs not to be defined
N=4
A(1,1)=-7.7;
A(1,2)= 2.1;A(2,2)= 8.3;
A(1,3)=-3.7;A(2,3)=-16.;A(3,3)=-12.
A(1,4)= 4.4;A(2,4)= 4.6;A(3,4)=-1.04;A(4,4)=-3.7
!We print the matrix A before calling DSYEV since it is
!destroyed after the call.
do i=1,N
do j=i,N
print *,’A( ’,i,’ , ’,j,’ )=’,A(i,j)
enddo
enddo
!We ask for eigenvalues AND eigenvectors (JOBZ=’V’)
JOBZ=’V’; UPLO=’U’
print *,’COMPUTING WITH DSYEV:’
LDA=P !notice that LDA-> P>N !!
call DSYEV(JOBZ,UPLO,N,A,LDA,W,WORK,LWORK,INFO)
print *,’DSYEV: DONE. CHECKING NOW:’
!If INFO is nonzero, then there is an error:
if(INFO .ne. 0)then
print *,’DSYEV FAILED. INF0= ’,INFO
stop
endif
!Print results: W(I) has the eigenvalues:
print *,’DSYEV: DONE.:’
print *,’EIGENVALUES OF MATRIX:’
do i=1,N
print *,’LAMBDA(’,i,’)=’,W(i)
enddo
!Eigenvectors are in stored in the columns of A:
print *,’EIGENVECTORS OF MATRIX’
do J=1,N
print *,’EIGENVECTOR ’,j,’ FOR EIGENVALUE ’,W(j)
do i=1,N
print *,’V_’,j,’(’,i,’)= ’,A(i,j)
enddo
enddo
end program test_evs
The next step is to compile and link the program. In order to link the program
to Lapack we have to instruct the linker ld where to find the libraries Lapack and
BLAS
and link them to our program. A library contains compiled software in archives of
object files. The convention for their names in a Unix environment is to start with
the string “lib” followed by the name of the library and a .a or .so extension.
For example, in our case the files we are interested in have the names
liblapack.so and libblas.so which can be searched in the file system by the
commands:
> locate libblas
> locate liblapack
In order to see the files that they contain we give the
commands :
> ar -t /usr/lib/libblas.so
> ar -t /usr/lib/liblapack.so
In the commands shown above you may have to substitute /usr/lib with the
path appropriate for your system. If the program is in the file test.f90, the
compilation/linking command is:
> gfortran test.f90 -o test -L/usr/lib -llapack -lblas
The option -L/usr/lib instructs the linker to look for libraries in the /usr/lib
directory ,
whereas the options -llapack -lblas instructs the linker to look for any
unresolved symbols (i.e. names of external functions and subroutines not coded in
our program) first in the library liblapack.a and then in the library
libblas.a.
The command shown above produces the executable file test which, when
run, produces the result:
EIGENVALUES OF MATRIX:
LAMBDA( 1)= -21.4119907
LAMBDA( 2)= -9.93394359
LAMBDA( 3)= -2.55765591
LAMBDA( 4)= 18.8035905
EIGENVECTORS OF MATRIX
EIGENVECTOR 1 FOR EIGENVALUE -21.4119907
V_ 1( 1)= -0.197845668
V_ 1( 2)= -0.464798676
V_ 1( 3)= -0.854691009
V_ 1( 4)= 0.119676904
EIGENVECTOR 2 FOR EIGENVALUE -9.93394359
V_ 2( 1)= 0.824412399
V_ 2( 2)= -0.132429396
V_ 2( 3)= -0.191076519
V_ 2( 4)= -0.516039161
EIGENVECTOR 3 FOR EIGENVALUE -2.55765591
V_ 3( 1)= 0.502684215
V_ 3( 2)= -0.247784372
V_ 3( 3)= 0.132853329
V_ 3( 4)= 0.817472616
EIGENVECTOR 4 FOR EIGENVALUE 18.8035905
V_ 4( 1)= 0.168848655
V_ 4( 2)= 0.839659187
V_ 4( 3)= -0.464050682
V_ 4( 4)= 0.226096318
We are now ready to tackle the problem of computing the energy spectrum of the
anharmonic oscillator. The main program contains the user interface where the
basic parameters for the calculation are read from the stdin. The user can
specify the dimension DIM  of
of  and the coupling constant
and the coupling constant  .
Then the program computes the eigenvalues
.
Then the program computes the eigenvalues  of the
of the  matrix
matrix  , which represents the action of the operator
, which represents the action of the operator  in the
in the
 representation in
representation in  . The tasks are allocated to the
subroutines calculate_X4, calculate_evs and calculate_H. The subroutine
calculate_X4 calculates the
. The tasks are allocated to the
subroutines calculate_X4, calculate_evs and calculate_H. The subroutine
calculate_X4 calculates the  matrix
matrix  . First, the matrix
. First, the matrix  is
calculated and then
is
calculated and then  is obtained by computing its fourth power. The
matrix
is obtained by computing its fourth power. The
matrix  can also be calculated analytically and this is left as an
exercise to the reader. The subroutine calculate_H calculates the matrix
can also be calculated analytically and this is left as an
exercise to the reader. The subroutine calculate_H calculates the matrix
 using the result for
using the result for  given by calculate_X4. Finally
the eigenvalues are calculated in the subroutine calculate_evs by a
call to DSYEV, which are returned to the main program for printing to
the stdout. The program is listed below and can be found in the file
anharmonic.f90:
given by calculate_X4. Finally
the eigenvalues are calculated in the subroutine calculate_evs by a
call to DSYEV, which are returned to the main program for printing to
the stdout. The program is listed below and can be found in the file
anharmonic.f90:
!========================================================
program anharmonic_elevels
!========================================================
implicit none
integer,parameter :: P = 1000
integer,parameter :: LWORK = 3*P-1
integer :: DIM
real(8),dimension(P,P) :: H,X,X4 !Hamiltionian+Position Ops
real(8),dimension(P) :: E !energy eigenvalues
real(8),dimension(LWORK):: WORK
real(8) :: lambda
integer :: i
print *,’# Enter Hilbert Space dimension:’
read *,DIM
print *,’# Enter lambda:’
read *,lambda
print *,’# lambda= ’,lambda
!Print Message:
print *,’# ################################################’
print *,’# Energy spectrum of anharmonic oscillator’
print *,’# using matrix methods.’
print *,’# Hilbert Space Dimension DIM = ’,DIM
print *,’# lambda coupling = ’,lambda
print *,’# ################################################’
print *,’# Outpout: DIM lambda E_0 E_1 .... E_{N-1}’
print *,’# ------------------------------------------------’
!Calculate X^4 operator:
call calculate_X4(X,X4,DIM)
!Calculate eigenvalues:
call calculate_evs(H,X4,E,WORK,lambda,DIM)
write(6,100)’EV ’,DIM,lambda,(E(i),i=1,DIM)
100 FORMAT(A3,I8,20000G25.15)
end program anharmonic_elevels
!========================================================
subroutine calculate_evs(H,X4,E,WORK,lambda,DIM)
!========================================================
implicit none
integer,parameter :: P = 1000
integer,parameter :: LWORK = 3*P-1
real(8),dimension(P,P) :: H,X4
real(8),dimension(P) :: E
real(8),dimension(LWORK) :: WORK
integer :: DIM
real(8) :: lambda
character(1) :: JOBZ,UPLO
integer :: LDA,INFO,i,j
call calculate_H(H,X4,lambda,DIM)
JOBZ=’V’;UPLO=’U’
call DSYEV(JOBZ,UPLO,DIM,H,P,E,WORK,LWORK,INFO)
print *,’# ********************** EVEC *******************’
do j=1,DIM
write(6,101)’# EVEC ’,lambda,(H(i,j), i=1,DIM)
enddo
print *,’# ********************** EVEC *******************’
101 FORMAT(A7,F15.3,20000G14.6)
!If INFO is nonzero then we have an error
if(INFO .ne. 0)then
print *,’dsyev failed. INFO= ’,INFO
stop
endif
end subroutine calculate_evs
!========================================================
subroutine calculate_H(H,X4,lambda,DIM)
!========================================================
implicit none
integer,parameter :: P = 1000
real(8),dimension(P,P) :: H,X4
integer :: DIM
real(8) :: lambda
integer :: i,j
do j=1,DIM
do i=1,DIM
H(i,j)=lambda*X4(i,j)
enddo
H(j,j) = H(j,j) + DBLE(j) - 0.5D0 !E_n=n+1/2,n=j-1=>E_n=j-1/2
enddo
print *,’# ********************** H *******************’
do j=1,DIM
write(6,102)’# HH ’,(H(i,j), i=1,DIM)
enddo
print *,’# ********************** H *******************’
102 FORMAT(A5,20000G20.6)
end subroutine calculate_H
!========================================================
subroutine calculate_X4(X,X4,DIM)
!========================================================
implicit none
integer,parameter :: P=1000
real(8),dimension(P,P):: X,X4,X2
integer :: DIM
integer :: i,j,m,n
real(8),parameter :: isqrt2=1.0D0/sqrt(2.0D0)
!Compute the position operator:
X = 0.0D0
!Compute the nonzero elements
do i=1,DIM
n=i-1 !indices 0,...,DIM-1
! The delta_{n,m+1} term, i.e. m=n-1
m=n-1 !the energy level n -> i=n+1, m-> j=m+1
j=m+1
if(j.ge.1 ) X(i,j)=isqrt2*sqrt(DBLE(m+1))
! The delta_{n,m-1} term, i.e. m=n+1
m=n+1
j=m+1
if(j.le.DIM) X(i,j)=isqrt2*sqrt(DBLE(m))
enddo
!Compute the Hamiltonian operator:
!Start with the X^4 operator:
X2 = MATMUL(X ,X ) !first X2,then X4:
X4 = MATMUL(X2,X2)
end subroutine calculate_X4
9.3 Results
Compiling and running the program can be done with the commands:
> gfortran -O2 anharmonic.f90 -o an -llapack -lblas
> ./an
# Enter Hilbert Space dimension:
4
# Enter lambda:
0.0
.....
# ********************** H *******************
# HH 0.50 0.00 0.00 0.00
# HH 0.00 1.50 0.00 0.00
# HH 0.00 0.00 2.50 0.00
# HH 0.00 0.00 0.00 3.50
# ********************** H *******************
# ********************** EVEC ****************
# EVEC 0.000 1.00 0.00 0.00 0.00
# EVEC 0.000 0.00 1.00 0.00 0.00
# EVEC 0.000 0.00 0.00 1.00 0.00
# EVEC 0.000 0.00 0.00 0.00 1.00
# ********************** EVEC ****************
EV 4 0.000 0.50 1.50 2.50 3.50
In the above program we used  and
and  . The
. The  choice leads us
to the simple harmonic oscillator and we obtain the expected solutions:
choice leads us
to the simple harmonic oscillator and we obtain the expected solutions:
 ,
,  and the eigenstates (eigenvectors of
and the eigenstates (eigenvectors of
 )
)  . Similar results can be obtained for larger
. Similar results can be obtained for larger
 .
.
For non zero values of  , the finite
, the finite  calculation contains systematic errors
from neglecting all the matrix elements
calculation contains systematic errors
from neglecting all the matrix elements  for
for  or
or  . Our
program calculates the eigenvalues
. Our
program calculates the eigenvalues  of the finite matrix
of the finite matrix  ,
,
 and one expects that
and one expects that
 | (9.22) |
where
 | (9.23) |
is the true  -th level eigenvalue of the Hamiltonian
-th level eigenvalue of the Hamiltonian  . In practice the limit
9.22 for given
. In practice the limit
9.22 for given  and
and  is calculated by computing
is calculated by computing  numerically for
increasing values of
numerically for
increasing values of  . If convergence to a desired level of accuracy is achieved
for the accessible values of
. If convergence to a desired level of accuracy is achieved
for the accessible values of  , then the approached limit is taken as an
approximation to
, then the approached limit is taken as an
approximation to  . This process is shown graphically in figures 9.1-9.3 for
. This process is shown graphically in figures 9.1-9.3 for
 . Convergence is satisfactory for quite small
. Convergence is satisfactory for quite small  for
for  but
larger values of
but
larger values of  are needed for
are needed for  . Increasing the value of
. Increasing the value of  for fixed
for fixed
 makes the use of larger values of
makes the use of larger values of  necessary. Similarly for a given energy
level
necessary. Similarly for a given energy
level  , increasing
, increasing  also makes the use of larger values of
also makes the use of larger values of  necessary. A
session that computes this limit for the ground level energy
necessary. A
session that computes this limit for the ground level energy  is shown
below :
is shown
below :
> tcsh
> gfortran -O2 anharmonic.f90 -llapack -lblas -o an
> foreach N (4 8 12 16 24 32)
foreach? (echo $N;echo 0.9) |./an >> data
foreach? end
> grep ^EV data | awk ’{print $2,$4}’
4 0.711467845686790
8 0.786328966767866
12 0.785237674919165
16 0.784964461939594
24 0.785032515135677
32 0.785031492177730
> gnuplot
gnuplot> plot "<grep ^EV data | awk ’{print 1/$2,$4}’"
Further automation of this process can be found in the shell script file
anharmonic.csh in the accompanying software. We note the large  convergence of
convergence of  and that we can take
and that we can take  . For higher
accuracy, a computation using larger
. For higher
accuracy, a computation using larger  will be necessary.
will be necessary.
We can also compute the expectation values  of an operator
of an operator
 when the anharmonic oscillator is in a state
when the anharmonic oscillator is in a state  :
:
 | (9.24) |
In practice, the expectation value will be computed from the limit
 | (9.25) |
where  are the eigenvectors of the finite
are the eigenvectors of the finite  matrix
matrix  computed numerically by DSYEV. These are determined by their components
computed numerically by DSYEV. These are determined by their components
 , where
, where
 | (9.26) |
which are stored in the columns of the array H after the call to DSYEV:
 | (9.27) |
Substituting equation (9.26) to (9.24) we obtain
 | (9.28) |
and we can use (9.27) for the computation of the sum.
As an application, consider the expectation values of the operators  ,
,  and
and  . Taking into account that
. Taking into account that 
 , we obtain the uncertainties
, we obtain the uncertainties
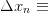

 and
and 
 . Their product
should satisfy Heisenberg’s uncertainty relation
. Their product
should satisfy Heisenberg’s uncertainty relation  . The results are
shown in table 9.1 and in figures 9.4-9.5. The calculation is left as an exercise to
the reader.
. The results are
shown in table 9.1 and in figures 9.4-9.5. The calculation is left as an exercise to
the reader.
The physics of the anharmonic oscillator can be better understood by studying
the large  limit. As shown in figure 9.5, the term
limit. As shown in figure 9.5, the term  dominates in this limit
and the expectation value
dominates in this limit
and the expectation value  decreases. This means that states that
confine the oscillator to a smaller range of
decreases. This means that states that
confine the oscillator to a smaller range of  are favored. This, using the
uncertainty principle, implies that the typical momentum of the oscillator
also increases in magnitude. This is confirmed in figure 9.5 where we
observe the expectation value
are favored. This, using the
uncertainty principle, implies that the typical momentum of the oscillator
also increases in magnitude. This is confirmed in figure 9.5 where we
observe the expectation value  to increase with
to increase with  . In order to
understand quantitatively these competing effects we will use a scaling
argument due to Symanzik. We redefine
. In order to
understand quantitatively these competing effects we will use a scaling
argument due to Symanzik. We redefine  ,
,  in the
Hamiltonian
in the
Hamiltonian  and for large enough
and for large enough  we
obtain
the asymptotic behavior
we
obtain
the asymptotic behavior
 | (9.29) |
where  is the Hamiltonian of the anharmonic “oscillator” with
is the Hamiltonian of the anharmonic “oscillator” with
 . Since the operator
. Since the operator  is independent of
is independent of  , the energy spectrum will
have the asymptotic behavior
, the energy spectrum will
have the asymptotic behavior
 | (9.30) |
In reference [42] it is shown that for  we have that
we have that
 | (9.31) |
with an accuracy better than one part in  . For large values of
. For large values of  , the authors
obtain the asymptotic behavior
, the authors
obtain the asymptotic behavior
 | (9.32) |
where 
 . This relation is tested
in figure 9.6 where we observe good agreement with our calculations.
. This relation is tested
in figure 9.6 where we observe good agreement with our calculations.
Table 9.2: Numerical calculation of the energy levels of the anharmonic oscillator given
in reference [42].
|
|
|
|
|
|
 |  |  |  |  |  |
|
|
|
|
|
|
| 0.002 | 0.501 489 66 | 1.507 419 39 | 2.519 202 12 | 3.536 744 13 | 4.559 955 56 |
| 0.006 | 0.504 409 71 | 1.521 805 65 | 2.555 972 30 | 3.606 186 33 | 4.671 800 37 |
| 0.01 | 0.507 256 20 | 1.535 648 28 | 2.590 845 80 | 3.671 094 94 | 4.774 913 12 |
| 0.05 | 0.532 642 75 | 1.653 436 01 | 2.873 979 63 | 4.176 338 91 | 5.549 297 81 |
| 0.1 | 0.559 146 33 | 1.769 502 64 | 3.138 624 31 | 4.628 882 81 | 6.220 300 90 |
| 0.3 | 0.637 991 78 | 2.094 641 99 | 3.844 782 65 | 5.796 573 63 | 7.911 752 73 |
| 0.5 | 0.696 175 82 | 2.324 406 35 | 4.327 524 98 | 6.578 401 95 | 9.028 778 72 |
| 0.7 | 0.743 903 50 | 2.509 228 10 | 4.710 328 10 | 7.193 265 28 | 9.902 610 70 |
| 1 | 0.803 770 65 | 2.737 892 27 | 5.179 291 69 | 7.942 403 99 | 10.963 5831 |
| 2 | 0.951 568 47 | 3.292 867 82 | 6.303 880 57 | 9.727 323 19 | 13.481 2759 |
| 50 | 2.499 708 77 | 8.915 096 36 | 17.436 9921 | 27.192 6458 | 37.938 5022 |
| 200 | 3.930 931 34 | 14.059 2268 | 27.551 4347 | 43.005 2709 | 60.033 9933 |
| 1000 | 3.694 220 85 | 23.972 2061 | 47.017 3387 | 73.419 1140 | 102.516 157 |
| 8000 | 13.366 9076 | 47.890 7687 | 93.960 6046 | 146.745 512 | 204.922 711 |
| 20000 | 18.137 2291 | 64.986 6757 | 127.508 839 | 199.145 124 | 278.100 238 |
|
|
|
|
|
|
 |  |  |  |  | |
|
|
|
|
|
|
| 0.002 | 5.588 750 05 | 6.623 044 60 | 7.662 759 33 | 8.707 817 30 | |
| 0.006 | 5.752 230 87 | 6.846 948 47 | 7.955 470 29 | 9.077 353 66 | |
| 0.01 | 5.901 026 67 | 7.048 326 88 | 8.215 837 81 | 9.402 692 31 | |
| 0.05 | 6.984 963 10 | 8.477 397 34 | 10.021 9318 | 11.614 7761 | |
| 0.1 | 7.899 767 23 | 9.657 839 99 | 11.487 3156 | 13.378 9698 | |
| 0.3 | 10.166 4889 | 12.544 2587 | 15.032 7713 | 17.622 4482 | |
| 0.5 | 11.648 7207 | 14.417 6692 | 17.320 4242 | 20.345 1931 | |
| 0.7 | 12.803 9297 | 15.873 6836 | 19.094 5183 | 22.452 9996 | |
| 1 | 14.203 1394 | 17.634 0492 | 21.236 4362 | 24.994 9457 | |
| 2 | 17.514 1324 | 21.790 9564 | 26.286 1250 | 30.979 8830 | |
| 50 | 49.516 4187 | 61.820 3488 | 74.772 8290 | 88.314 3280 | |
| 200 | 78.385 6232 | 97.891 3315 | 118.427 830 | 139.900 400 | |
| 1000 | 133.876 891 | 167.212 258 | 202.311 200 | 239.011 580 | |
| 8000 | 267.628 498 | 334.284 478 | 404.468 350 | 477.855 700 | |
| 20000 | 363.201 843 | 453.664 875 | 548.916 140 | 648.515 330 | |
| |
|
|
|
|
|
|
9.4 The Double Well Potential
We can also use matrix methods in order to calculate the energy spectrum of a
particle in a double well potential given by the Hamiltonian:
 | (9.33) |
The equilibrium points of the classical motion are located at the minima:
 | (9.34) |
When the well is very deep, then for the lowest energy levels the potential can
be well approximated by that of a harmonic oscillator with angular frequency
 , therefore
, therefore
 | (9.35) |
In this case the tunneling effect is very weak and the energy levels are arranged in
almost degenerate pairs. The corresponding eigenstates are symmetric and
antisymmetric linear combinations of states localized near the left and right
minima of the potential. For example, for the two lowest energy levels we expect
that
 | (9.36) |
where  and
and
 | (9.37) |
where the states  and
and  are localized to the left and right well of the
potential respectively (see also figure 10.4 of chapter 10).
are localized to the left and right well of the
potential respectively (see also figure 10.4 of chapter 10).
We will use equations (9.12) in order to calculate the Hamiltonian (9.33) .
We need to make very small modifications to the code in the file anharmonic.f90.
We will only add a routine that calculates the matrices  . The resulting
program can be found in the file doublewell.f90:
. The resulting
program can be found in the file doublewell.f90:
!========================================================
program doublewell_elevels
!========================================================
! H : Hamiltonian operator H0+(lambda/4)*X^4
! H0 : Hamiltonian H0=1/2 P^2-1/2 X^2
! X,X2,X4: Position operator and its powers
! iP : i P operator
! P2 : P^2 = -(iP)(iP) operator
! E : Energy eigenvalues
! WORK : Workspace for lapack routine DSYEV
!========================================================
implicit none
integer,parameter :: P=1000
integer,parameter :: LWORK=3*P-1
real(8),dimension(P,P) :: H,H0,X,X4,X2,iP,P2
real(8),dimension(P) :: E
real(8),dimension(LWORK):: WORK
real(8) :: lambda,lambda0,lambdaf,dlambda
integer :: DIM0,DIMF,dDIM,DIM
integer :: i
!Minimum and maximum values of Hilbert space dimensions:
print *,’Enter Hilbert Space dimensions (DIM0,DIMF,DDIM):’
read *,DIM0,DIMF,DDIM
!Minimum and maximum values of lambda (step dlambda):
print *,’Enter lambda0,lambdaf,dlambda:’
read *,lambda0,lambdaf,dlambda
print *,’lambda0= ’,lambda0
!Print Message:
print *,’# ################################################’
print *,’# Energy levels of double well potential’
print *,’# using matrix methods.’
print *,’# Hilbert Space Dimensions = ’,DIM0,’ - ’,DIMF,&
’ step= ’,dDIM
print *,’# lambda coupling = ’,lambda0,’ - ’,lambdaf,&
’ step= ’,dlambda
print *,’# ################################################’
print *,’# Outpout: DIM lambda E_0 E_1 .... E_{N-1}’
print *,’# ------------------------------------------------’
do DIM=DIM0,DIMF,dDIM
call calculate_operators(X,X2,X4,iP,P2,H0,DIM)
lambda = lambda0
do while (lambda .le. lambdaf )
call calculate_evs(H,H0,X4,E,WORK,lambda,DIM)
write(6,100)’EV ’,DIM,lambda,(E(i),i=1,DIM)
lambda = lambda+dlambda
enddo
enddo
100 FORMAT(A3,I5,1000G25.15)
end program doublewell_elevels
!========================================================
subroutine calculate_evs(H,H0,X4,E,WORK,lambda,DIM)
!========================================================
implicit none
integer,parameter :: P=1000
integer,parameter :: LWORK=3*P-1
real(8),dimension(P,P) :: H,H0,X4
real(8),dimension(P) :: E
real(8),dimension(LWORK) :: WORK
integer :: DIM
real(8) :: lambda
character(1) :: JOBZ,UPLO
integer :: LDA,INFO,i,j
call calculate_H(H,H0,X4,lambda,DIM)
JOBZ=’V’;UPLO=’U’
call DSYEV(JOBZ,UPLO,DIM,H,P,E,WORK,LWORK,INFO)
print *,’# ********************** EVEC *******************’
do j=1,DIM
write(6,101)’# EVEC ’,DIM,lambda,(H(i,j), i=1,DIM)
enddo
print *,’# ********************** EVEC *******************’
101 FORMAT(A7,I5,F8.4,1000G14.6)
if(INFO .ne. 0)then
print *,’dsyev failed. INFO= ’,INFO
stop
endif
end subroutine calculate_evs
!========================================================
subroutine calculate_H(H,H0,X4,lambda,DIM)
!========================================================
implicit none
integer,parameter :: P=1000
real(8),dimension(P,P) :: H,H0,X4
integer :: DIM
real(8) :: lambda
integer :: i,j
do j=1,DIM
do i=1,DIM
H(i,j)=H0(i,j)+0.25D0*lambda*X4(i,j)
enddo
enddo
print *,’# ********************** H *******************’
do j=1,DIM
write(6,102)’# HH ’,(H(i,j), i=1,DIM)
enddo
print *,’# ********************** H *******************’
102 FORMAT(A5,1000G14.6)
end subroutine calculate_H
!========================================================
subroutine calculate_operators(X,X2,X4,iP,P2,H0,DIM)
!========================================================
implicit none
integer,parameter :: P=1000
real(8),dimension(P,P) :: X,X4,X2,iP,P2,H0
integer :: DIM
integer :: i,j,m,n
real(8),parameter :: isqrt2=1.0D0/sqrt(2.0D0)
X =0.0D0;X2=0.0D0;X4=0.0D0
iP=0.0D0;P2=0.0D0
do i=1,DIM
n=i-1 !indices 0,...,DIM-1
! The delta_{n,m+1} term, i.e. m=n-1
m=n-1 !energy level: n -> i=n+1, m-> j=m+1
j=m+1
if(j.ge.1) X (i,j) = isqrt2*sqrt(DBLE(m+1))
if(j.ge.1) iP(i,j) = -isqrt2*sqrt(DBLE(m+1))
! The delta_{n,m-1} term, i.e. m=n+1
m=n+1
j=m+1
if(j.le.DIM) X (i,j) = isqrt2*sqrt(DBLE(m))
if(j.le.DIM) iP(i,j) = isqrt2*sqrt(DBLE(m))
enddo !do i=1,DIM
X2 = MATMUL( X, X)
P2 = -MATMUL(iP,iP)
X4 = MATMUL(X2,X2)
!The Hamiltionian:
H0 = 0.5D0*(P2-X2)
end subroutine calculate_operators
Where is the particle’s favorite place when it is in the states  and
and  ? The
answer to this question is obtained from the study of the expectation value of the
position operator
? The
answer to this question is obtained from the study of the expectation value of the
position operator  in each one of them. We know that when the particle is in
one of the energy eigenstates, then we have that
in each one of them. We know that when the particle is in
one of the energy eigenstates, then we have that
 | (9.38) |
because the potential  is even. Therefore
is even. Therefore
where in the last line we used the relation (9.38) 
 and that the amplitudes
and that the amplitudes 
 .
Also
we have that
.
Also
we have that  . Therefore, if we have that
. Therefore, if we have that  and
and
 , we obtain
, we obtain
 | (9.40) |
Given that for finite  , the subroutine DSYEV returns approximations to the
coefficients
, the subroutine DSYEV returns approximations to the
coefficients  in the columns of the matrix H(DIM,DIM) so that
in the columns of the matrix H(DIM,DIM) so that  H(m+1,n+1), you may compare the value of
H(m+1,n+1), you may compare the value of  with the classical values
with the classical values
 as
as  is increased.
is increased.
9.5 Problems
- Calculate the matrix
 for
for  analytically. Calculate its
eigenvalues for
analytically. Calculate its
eigenvalues for  . Compare your results with the numerical values
that you obtain from your program.
. Compare your results with the numerical values
that you obtain from your program.
- Add the necessary code to the program in the file test.f90 so that it
checks that the eigenvectors satisfy their defining relations
 and that they form an orthonormal basis
and that they form an orthonormal basis  .
.
- Calculate
 and
and  for
for  with an accuracy better
than
with an accuracy better
than  %.
%.
- For how large
 can you calculate
can you calculate  for
for  with an accuracy
better than
with an accuracy
better than  % when
% when  ?
?
- Calculate
 and
and  for
for  with step
with step  by
achieving accuracy better than
by
achieving accuracy better than  %. How large should
%. How large should  be taken
in each case?
be taken
in each case?
- Calculate the expression that gives the matrix elements of the operator
 in the
in the  representation analytically. Modify the program in
anharmonic.f90 in order to incorporate your calculation. Verify that
the results are the same and test if it has an effect in the total
computation time with and without calculating the eigenvalues and
eigenvectors of the Hamiltonian. Compute in each case the dependence
of the cpu time on
representation analytically. Modify the program in
anharmonic.f90 in order to incorporate your calculation. Verify that
the results are the same and test if it has an effect in the total
computation time with and without calculating the eigenvalues and
eigenvectors of the Hamiltonian. Compute in each case the dependence
of the cpu time on  by computing the exponent (cpu time)
by computing the exponent (cpu time) for
for  .
.
- Modify the code in the file anharmonic.f90 so that the arrays H, X,
X4, E, WORK are ALLOCATABLE and their dimension is determined by
the variable DIM read by the program interactively.
(Hint: Look at the file anharmonicSPEED.f90.)
- Make an attempt to reproduce the results of Hioe and Montroll [42]
given in table 9.2 for
 and
and  . What is the largest value of
. What is the largest value of
 that you can study given your computational resources?
that you can study given your computational resources?
- Make an attempt to reproduce the results of Hioe and Montroll [42]
given by equation (9.31) . Calculate the ground state energy
 for
for
 and then fit your results to a function of the form
and then fit your results to a function of the form
 . What is the accuracy in the calculation of
the coefficients
. What is the accuracy in the calculation of
the coefficients  ,
,  and
and  and how good is the agreement with
equation (9.31) ?
and how good is the agreement with
equation (9.31) ?
- Modify the code in the file anharmonic.f90 so that it calculates the
expectation values
 ,
,  and the corresponding
products
and the corresponding
products  .
.
(Hint: See the file anharmonicOBS.f90.)
- Reproduce the results shown in figure 9.4. Repeat your calculation for
 . Repeat your calculations for
. Repeat your calculations for  .
.
- Reproduce the results shown in figure 9.5. Repeat your calculations for
 .
.
- Reproduce the results shown in figure 9.6. Repeat your calculation for
 .
.
- Write a program that calculates the energy levels of the anharmonic
oscillator
 | (9.41) |
Calculate  for
for  ,
,  and
and  .
.
- Modify the program of the previous problem so that it calculates the
expectation values
 ,
,  and the products
and the products  .
Calculate the expectation values
.
Calculate the expectation values  ,
,  and
and  for
for
 ,
,  and
and  .
.
- Use the program doublewell.f90 in order to calculate the energy
level pairs
 for
for  and
and  .
Calculate the difference
.
Calculate the difference 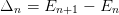 and comment on your
results.
and comment on your
results.
- Define the energy values
 Compare the results for
Compare the results for  of the previous problem with
of the previous problem with
 and
and  respectively. Explain your results.
respectively. Explain your results.
- Modify the program doublewell.f90, so that it calculates the expectation
values
 given by equation (9.40) . Compare
given by equation (9.40) . Compare  with the
classical values
with the
classical values  for
for  .
.
- Repeat the previous problem when the states
 for
for  and
and  .
.
- For the simple harmonic oscillator, the energy levels are equidistant,
i.e.
 ,
,  . Calculate these
quantities for the anharmonic oscillator and the double well potential for
. Calculate these
quantities for the anharmonic oscillator and the double well potential for
 and
and  . What do you conclude from your
results?
. What do you conclude from your
results?
Chapter 10
Time Independent Schrödinger Equation
In this chapter, we will study the time independent Schrödinger equation
for a non relativistic particle of mass  , without spin, moving in one
dimension, in a static potential
, without spin, moving in one
dimension, in a static potential  . We will only study bound states. The
solutions in this case yield the discrete energy spectrum
. We will only study bound states. The
solutions in this case yield the discrete energy spectrum  as well as
the corresponding eigenstates of the Hamiltonian
as well as
the corresponding eigenstates of the Hamiltonian  in position
representation.
in position
representation.
From a numerical analysis point of view, the problem consists of solving for
the eigensystem of a differential equation with boundary conditions. Part of the
solution is the energy eigenvalue which also needs to be determined.
As an exercise, we will use two different methods, one that can be applied to a
particle in an infinite well with  , and one that can be applied to
more general cases. The first method is introduced only for educational
purposes and the reader may skip section 10.2 to go directly to section
10.3.
, and one that can be applied to
more general cases. The first method is introduced only for educational
purposes and the reader may skip section 10.2 to go directly to section
10.3.
10.1 Introduction
The wave functions  , which are the position representation of the energy
eigenstates, satisfy the Schrödinger equation
, which are the position representation of the energy
eigenstates, satisfy the Schrödinger equation
 | (10.1) |
with the normalization condition
 | (10.2) |
The Hamiltonian operator is given in position representation by
 | (10.3) |
and it is Hermitian, i.e.  . Equation (10.1) is an eigenvalue
problem
. Equation (10.1) is an eigenvalue
problem
 | (10.4) |
which, for bound states, has as solutions a discrete set of real functions
 such that
such that  . The numbers
. The numbers  are real and they are the (bound) energy spectrum of the particle in the
potential
are real and they are the (bound) energy spectrum of the particle in the
potential
 . The minimum energy
. The minimum energy  is called the ground state energy and the
corresponding ground state is given by a non trivial function
is called the ground state energy and the
corresponding ground state is given by a non trivial function  . According to
the Heisenberg uncertainty principle, in this state the uncertainties in momentum
. According to
the Heisenberg uncertainty principle, in this state the uncertainties in momentum
 and position
and position  so that
so that  .
.
The eigenstates  form an orthonormal basis
form an orthonormal basis
 | (10.5) |
so that any (square integrable) wave function  which represents the state
which represents the state
 is given by the linear combination
is given by the linear combination
 | (10.6) |
The amplitudes 
 are complex numbers
that give the probability
are complex numbers
that give the probability  to measure energy
to measure energy  in the state
in the state
 .
.
For any state  the function
the function
 | (10.7) |
is the probability density of finding the particle at position  , i.e. the probability
of detecting the particle in the interval
, i.e. the probability
of detecting the particle in the interval ![[x1,x2]](main_latex3580x.png) is given by
is given by
 | (10.8) |
The normalization condition (10.2) reflects the conservation of probability
(independent of time, respected by the time dependent Schrödinger equation) and
the completeness (in this case the certainty that the particle will be observed
somewhere on the  axis).
axis).
The classical observables  of this quantum mechanical system are
functions of the position and the momentum and their quantum mechanical
versions are given by operators
of this quantum mechanical system are
functions of the position and the momentum and their quantum mechanical
versions are given by operators  . Their expectation values when the
system in a state
. Their expectation values when the
system in a state  are given by
are given by
 | (10.9) |
From a numerical point of view, the eigenvalue problem (10.1) requires the
solution of an ordinary second order differential equation. There are certain
differences in this problem compared to the ones studied in previous sections:
- Instead of an initial value problem (i.e. the values of the function and its
derivative are given at one point), we have a boundary value problem
(values of the function or its derivative given at two different points).
- The eigenvalue (energy) is unknown and should be determined as part
of the solution.
As an introduction to such classes of problems, we will present some simple methods
which are special to one dimension.
For the numerical solution of the above equation we renormalize  , the
function
, the
function  and the parameters so that we deal only with dimensionless
quantities. Equation (10.1) is rewritten as:
and the parameters so that we deal only with dimensionless
quantities. Equation (10.1) is rewritten as:
 | (10.10) |
Then we choose a length scale  which is defined by the parameters of the
problem
and we redefine
which is defined by the parameters of the
problem
and we redefine  . We define
. We define 
 and we obtain
and we obtain
 | (10.11) |
We define 
 ,
,  and
change notation to
and
change notation to  ,
,  . We obtain
. We obtain
 | (10.12) |
The solutions of equation (10.1) can be obtained from those of equation (10.12) by using the
following “dictionary” :
 | (10.13) |
The dimensionless momentum is defined as 
 and we
obtain
and we
obtain
 | (10.14) |
The commutation relation ![[x, p] = iℏ](main_latex3613x.png) becomes
becomes ![[˜x, ˜p] = i](main_latex3614x.png) . The kinetic energy
. The kinetic energy
 is given by
is given by
 | (10.15) |
and the Hamiltonian 
 | (10.16) |
In what follows, we will omit the tilde above the symbols and write  instead of
instead of
 .
.
10.2 The Infinite Potential Well
The simplest model for studying the qualitative features of bound states is the
infinite potential well of width  where a particle is confined within the interval
where a particle is confined within the interval
![[− L∕2,L ∕2]](main_latex3622x.png) :
:
 | (10.17) |
The length scale chosen here is  and the dimensionless variable
and the dimensionless variable  corresponds to
corresponds to  when
when  is measured in length units.
is measured in length units.
The solution of (10.12) can be easily computed. Due to the symmetry
 | (10.18) |
of the potential, the solutions have well defined parity. This property will be
crucial to the method used below. The method discussed in the next section can
also be used on non even potentials.
The solutions are divided into two categories, one with even parity

 for
for  and one with odd parity
and one with odd parity

 for
for  .
.
 | (10.19) |
where
 | (10.20) |
and the normalization has been chosen so
that
 .
.
The solutions can be found by using the parity of the wave functions. We note
that for the positive parity solutions
 | (10.21) |
whereas for the negative parity solutions
 | (10.22) |
The constant  depends on the normalization of the wave function. Therefore
we can set
depends on the normalization of the wave function. Therefore
we can set  originally and then renormalize the wave function so
that equation (10.2) is satisfied. If the energy is known, the relations
(10.21) and (10.22) can be taken as initial conditions in relation (10.12) .
By using a Runge–Kutta algorithm we can evolve the solution towards
originally and then renormalize the wave function so
that equation (10.2) is satisfied. If the energy is known, the relations
(10.21) and (10.22) can be taken as initial conditions in relation (10.12) .
By using a Runge–Kutta algorithm we can evolve the solution towards
 . The problem is that the energy
. The problem is that the energy  is unknown. If the energy
is not allowed by the quantum theory we will find that the boundary
conditions
is unknown. If the energy
is not allowed by the quantum theory we will find that the boundary
conditions
 | (10.23) |
are violated. As we approach the correct value of the energy, we obtain
 .
.
Therefore we follow the steps described below:
- We choose an initial value for the energy
 that is lower than the
one we are looking for. We can use estimates from known solutions
of similar looking potential wells or simply start from a value slightly
higher than the absolute minimum of the potential.
that is lower than the
one we are looking for. We can use estimates from known solutions
of similar looking potential wells or simply start from a value slightly
higher than the absolute minimum of the potential.
- We choose the parity of the solution and we set initial conditions
according to equations (10.21) and (10.22) .
- We evolve the solutions using a 4th order Runge-Kutta method from
 to
to  .
.
- If equation (10.23) is not satisfied, we increase the energy by
 and
we repeat.
and
we repeat.
- We repeat until
 changes sign. Then we lower the energy by
changes sign. Then we lower the energy by
 .
.
- The process is ended when
 for appropriately chosen
small
for appropriately chosen
small  .
.
For the evolution of the solution from  to
to  we use the 4th order
Runge-Kutta method programmed in the file rk.f90 of chapter 4. We copy the
subroutine RKSTEP in a local file rk.f90. The integration of (10.12) can by done
by using the function
we use the 4th order
Runge-Kutta method programmed in the file rk.f90 of chapter 4. We copy the
subroutine RKSTEP in a local file rk.f90. The integration of (10.12) can by done
by using the function 
with the initial conditions We use the notation  psi,
psi,  psip. The functions f1 and f2
correspond to the right hand side of (10.24) . They are the derivatives of
psip. The functions f1 and f2
correspond to the right hand side of (10.24) . They are the derivatives of
 and
and  respectively and f1=psip, f2=(V-energy)*psi. The
code of f1 and f2 is put in a different file so that we can easily reuse
the code for many different potentials
respectively and f1=psip, f2=(V-energy)*psi. The
code of f1 and f2 is put in a different file so that we can easily reuse
the code for many different potentials  . The file wellInfSq.f90
contains the necessary program for the potential of equation (10.17)
:
. The file wellInfSq.f90
contains the necessary program for the potential of equation (10.17)
:
!===========================================================
!file: wellInfSq.f
!
!Functions used in RKSTEP routine. Here:
!f1 = psip(x) = psi(x)’
!f2 = psip(x)’= psi(x)’’
!
!All one has to set is V, the potential
!===========================================================
!-------- trivial function: derivative of psi
real(8) function f1(x,psi,psip)
real(8) :: x,psi,psip
f1=psip
end function f1
!===========================================================
!-------- the second derivative of wavefunction:
!psip(x)’ = psi(x)’’ = -(E-V) psi(x)
real(8) function f2(x,psi,psip)
implicit none
real(8) :: x,psi,psip,energy,V
common /params/energy
!------- potential, set here:
V = 0.0D0
!------- Schroedinger eq: RHS
f2 = (V-energy)*psi
end function f2
!===========================================================
We stress that the energy  energy is put in a common block so that it can
be accessed by the main program.
energy is put in a common block so that it can
be accessed by the main program.
The main program is in the file well.f90. The user enters the parameters
(energy, parity, Nx) and the loop
do while (iter .lt. 10000)
............
if(DABS(psinew) .le. epsilon) EXIT
if(psinew*psiold .lt. 0.0D0 ) de = -0.5D0*de
energy = energy + de
............
enddo ! do while
exits when  psinew has an absolute value which is less than epsilon, i.e.
when the condition (10.23) is satisfied to the desired accuracy. The value of the
energy increases up to the point where the sign of the wave function at
psinew has an absolute value which is less than epsilon, i.e.
when the condition (10.23) is satisfied to the desired accuracy. The value of the
energy increases up to the point where the sign of the wave function at  changes (psinew*psiold
changes (psinew*psiold ). Then the value of the energy is overestimated
and we change the sign of the step de and reduce its magnitude by a half. The
algorithm described on page 1064 is implemented inside the loop. After exiting
the loop, the energy has been determined with the desired accuracy and the rest
of the program stores the solution in the array psifinal(STEPS). The results
are written to the file psi.dat. Note how the variable parity is used so
that both cases parity
). Then the value of the energy is overestimated
and we change the sign of the step de and reduce its magnitude by a half. The
algorithm described on page 1064 is implemented inside the loop. After exiting
the loop, the energy has been determined with the desired accuracy and the rest
of the program stores the solution in the array psifinal(STEPS). The results
are written to the file psi.dat. Note how the variable parity is used so
that both cases parity can be studied. The full program is listed
below:
can be studied. The full program is listed
below:
!===========================================================
!file: well.f
!
!Computation of energy eigenvalues and eigenfunctions
!of a particle in an infinite well with V(-x)=V(x)
!
!Input: energy: initial guess for energy
! parity: desired parity of solution (+/- 1)
! Nx-1 : Number of RK4 steps from x=0 to x=1
!Output: energy: energy eigenvalue
! psi.dat: final psi(x)
! all.dat: all psi(x) for trial energies
!===========================================================
program even_potential_well
implicit none
integer,parameter :: P=10000
real(8) :: energy,dx,x,epsilon,de
common /params/energy
integer :: parity,Nx,iter,i
real(8) :: psi,psip,psinew,psiold
real(8) :: psifinal(-P:P),xstep(-P:P)
!------ Input:
print *,’Enter energy,parity,Nx:’
read *, energy,parity,Nx
if(Nx .gt. P) stop ’Nx > P’
if(parity .gt. 0) then
parity = 1
else
parity = -1
endif
print *,’# #######################################’
print *,’# Estart= ’,energy,’ parity= ’,parity
dx = 1.0D0/(Nx-1)
epsilon = 1.0D-6
print *,’# Nx= ’,Nx ,’ dx = ’,dx,’ eps= ’,epsilon
print *,’# #######################################’
!----- Calculate:
open(unit=11,file=’all.dat’)
iter = 0
psiold = 0.0D0 ! calculated values of psi at x=1
psinew = 1.0D0
de = 0.1D0*DABS(energy) ! original change in energy
do while (iter .lt. 10000)
!---------- Initial conditions at x=0
x = 0.0D0
if(parity .eq. 1)then
psi = 1.0D0
psip = 0.0D0
else
psi = 0.0D0
psip = 1.0D0
endif
write(11,*) iter,energy, x, psi,psip
! --------- Use Runge-Kutta to forward to x=1
do i=2,Nx
x = (i-2)*dx
call RKSTEP(x,psi,psip,dx)
write(11,*) iter,energy,x,psi,psip
enddo ! do i=2,Nx
psinew = psi
print *,iter, energy, de,psinew
! --------- Stop if value of psi close to 0
if(DABS(psinew) .le. epsilon) EXIT
! --------- Change direction of energy search:
if(psinew*psiold .lt. 0.0D0 ) de = -0.5D0*de
energy = energy + de
psiold = psinew
iter = iter + 1
enddo ! do while
close(11)
!We found the solution: calculate it once again and store it
if(parity .eq. 1)then
psi = 1.0D0
psip = 0.0D0
node = 0 ! count number of nodes of function
else
psi = 0.0D0
psip = 1.0D0
node = 1
endif
x = 0.0D0
xstep (0) = x
psifinal(0) = psi ! array that stores psi(x)
psiold = 0.0D0
!------- Use Runge-Kutta to move to x=1
do i=2,Nx
x = (i-2)*dx
call RKSTEP(x,psi,psip,dx)
xstep (i-1) = x
psifinal(i-1) = psi
! ------ Use parity to compute psi(-x)
xstep (1-i) = -x
psifinal(1-i) = parity*psi
!------- Print final solution:
open(unit=11,file=’psi.dat’)
print *,’Final result: E= ’,energy,’ n= ’,node,&
’ parity= ’,parity
write(11,*)’# E= ’ ,energy,’ n= ’,node,&
’ parity= ’,parity
do i=-(Nx-1),(Nx-1)
write(11,*) xstep(i),psifinal(i)
enddo
close(11)
end program even_potential_well
The compilation and running of the program can be done with the commands
> gfortran well.f90 wellInfSq.f90 rk.f90 -o well
> ./well
Enter energy,parity,Nx:
2.0 1 400
# #######################################
# Estart= 2.0000000000000000 parity= 1
# Nx= 400 dx = 2.50626566416E-003 eps= 9.9999999999E-007
# #######################################
0 2.0000000000000 0.200000000000 0.15594369476721
1 2.2000000000000 0.200000000000 8.74448016806986E-2
............................................
28 2.4674072265624 1.220703125000E-5 -1.95005436858826E-6
29 2.4674011230468 -6.103515625000E-6 -7.24621589476086E-9
Final result: E= 2.4674011230468746 parity= 1
The energy is determined to be  2.467401123 which can be compared to the
exact value
2.467401123 which can be compared to the
exact value  2.467401100. The fractional error is
2.467401100. The fractional error is  . The
convergence can be studied graphically in figure 10.2.
. The
convergence can be studied graphically in figure 10.2.
The calculation of the excited states is done by changing the parity and by
choosing the initial energy slightly higher than the one determined in the previous
step .
The results are in table 10.1. The agreement with the exact result  is excellent.
is excellent.
We close this section with two more examples. First, we study a potential well
with triangular shape at its bottom
 | (10.26) |
and then a double well potential with
 | (10.27) |
where the parameters  are positive numbers. A qualitative plot of these
functions is shown in figure 10.1.
are positive numbers. A qualitative plot of these
functions is shown in figure 10.1.
For the triangular potential we take  , whereas for the double well
potential
, whereas for the double well
potential  and
and  . The code in wellInfSq.f90 is appropriately
modified and saved in the files wellInfTr.f90 and wellInfDbl.f90 respectively.
All we have to do is to change the line computing the value of the potential in the
function f2. For example the file wellInfTr.f90 contains the code
. The code in wellInfSq.f90 is appropriately
modified and saved in the files wellInfTr.f90 and wellInfDbl.f90 respectively.
All we have to do is to change the line computing the value of the potential in the
function f2. For example the file wellInfTr.f90 contains the code
!------- potential, set here:
V = 10.0D0*DABS(x)
whereas the file wellInfDbl.f90 contains the code
!------- potential, set here:
if( DABS(x) .le. 0.3D0)then
V = 100.0D0
else
V = 0.0D0
endif
The analysis is performed in exactly the same way and the results are shown in
table 10.1. Note that, for large enough  , the energy levels of all the potentials
that we studied above tend to have identical values. This happens because, when
the particle has energy much larger than
, the energy levels of all the potentials
that we studied above tend to have identical values. This happens because, when
the particle has energy much larger than  , the details of the potential at the
bottom do not influence its dynamical properties very much. For the triangular
potential, the energy levels have higher values than the corresponding ones of the
square potential. This happens because, on the average, the potential energy is
higher and the potential tends to confine the particle to a smaller region (
, the details of the potential at the
bottom do not influence its dynamical properties very much. For the triangular
potential, the energy levels have higher values than the corresponding ones of the
square potential. This happens because, on the average, the potential energy is
higher and the potential tends to confine the particle to a smaller region ( is
decreased, therefore
is
decreased, therefore  is increased). This can be seen in figure 10.3
where the wave functions of the particle in each of the two potentials are
compared.
is increased). This can be seen in figure 10.3
where the wave functions of the particle in each of the two potentials are
compared.
Similar observations can be made for the double well potential. Moreover, we
note the approximately degenerate energy levels, something which is expected for
potentials of this form. This can be understood in terms of the localized
states given by the wave functions  and
and
 . The first one represents a state where
the particle is localized in the left well and the second one in the right.
This is shown in figure 10.4. As
. The first one represents a state where
the particle is localized in the left well and the second one in the right.
This is shown in figure 10.4. As  the two wells decouple and
the wave functions
the two wells decouple and
the wave functions  become equal to the energy eigenstate wave
functions of two particles in separate infinite square wells of width
become equal to the energy eigenstate wave
functions of two particles in separate infinite square wells of width  with energy eigenvalues
with energy eigenvalues  . The difference of
. The difference of  and
and  from these two values is due to the finite
from these two values is due to the finite  (see problem 4).
(see problem 4).
We will now discuss the limitations of this method. First, the method can be
used only on potential wells that are even, i.e.  . We used this
assumption in equations (10.21) and (10.22) giving the initial conditions for
states of well defined parity. When the potential is even, the energy eigenstates
have definite parity. The other problem can be understood by solving problem 4:
When
. We used this
assumption in equations (10.21) and (10.22) giving the initial conditions for
states of well defined parity. When the potential is even, the energy eigenstates
have definite parity. The other problem can be understood by solving problem 4:
When  , the wave function is almost zero around
, the wave function is almost zero around  and
the integration from
and
the integration from  to
to  will be dominated by numerical
errors. The same is true when the particle has to go through high potential
barriers.
will be dominated by numerical
errors. The same is true when the particle has to go through high potential
barriers.
This method can also we used on potential wells that are not infinite. In that
case we can add infinite walls at points that are far enough so that the wave
function is practically zero there. Then the influence of this artificial wall will be
negligible (see problem 3).
10.3 Bound States
A serious problem with the method discussed in the previous section is that it
is numerically unstable. You should have already realized that if you tried to solve
problem 3. In that problem, when the walls are moved further than  , the
convergence of the algorithm becomes harder. You can understand this by
realizing that in the integration process the solution is evolved from the classically
allowed into the classically forbidden region so that an oscillating solution
changes into an exponentially damped one. But as
, the
convergence of the algorithm becomes harder. You can understand this by
realizing that in the integration process the solution is evolved from the classically
allowed into the classically forbidden region so that an oscillating solution
changes into an exponentially damped one. But as  there are two
solutions, one that is physically acceptable
there are two
solutions, one that is physically acceptable  and one that is
diverging
and one that is
diverging  which is not acceptable due to (10.2) . Therefore, in
order to achieve convergence to the physically acceptable solution, the
energy has to be finely tuned, especially when we integrate towards large
which is not acceptable due to (10.2) . Therefore, in
order to achieve convergence to the physically acceptable solution, the
energy has to be finely tuned, especially when we integrate towards large
 . For this reason it is preferable to integrate from the exponentially
damped region towards the oscillating region. The idea is to start integrating
from these regions and try to match the solutions and their derivatives at
appropriately chosen matching points. The matching is achieved at a
point
. For this reason it is preferable to integrate from the exponentially
damped region towards the oscillating region. The idea is to start integrating
from these regions and try to match the solutions and their derivatives at
appropriately chosen matching points. The matching is achieved at a
point  by trying to determine the value of the energy that sets the
ratio
by trying to determine the value of the energy that sets the
ratio
 | (10.28) |
equal to zero, within the attainable numerical accuracy. It is desirable to
choose a point  within the classical region (
within the classical region ( ) and usually
we pick a turning point
) and usually
we pick a turning point  . By renormalizing
. By renormalizing  we can
always set
we can
always set  , therefore
, therefore  means that
means that
 . The denominator of (10.28) sets the scale of the desired
accuracy
The idea is depicted in figure 10.5. The algorithm is the following:
. The denominator of (10.28) sets the scale of the desired
accuracy
The idea is depicted in figure 10.5. The algorithm is the following:
- Choose the integration interval [xmin,xmax].
- Choose the initial conditions
 ,
,  ,
,
 ,
,  . This choice depends on the potential
. This choice depends on the potential
 . Usually we take xmin and xmax deep enough in the classically
forbidden region and choose the values
. Usually we take xmin and xmax deep enough in the classically
forbidden region and choose the values 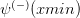 ,
,  to
be zero or exponentially small (e.g.
to
be zero or exponentially small (e.g.  ,
,  ). The
corresponding values of the derivatives
). The
corresponding values of the derivatives  ,
,  are also taken to be small. The arbitrary normalization of
are also taken to be small. The arbitrary normalization of  allows
these initial values to be chosen in a crude way. The relative sign of
the derivatives at large
allows
these initial values to be chosen in a crude way. The relative sign of
the derivatives at large  (determined e.g. by the parity of the wave
function for even potentials) is also taken care by the renormalization
of
(determined e.g. by the parity of the wave
function for even potentials) is also taken care by the renormalization
of  when applying the matching condition. For an infinite well,
the points xmin,xmax are the ones where the potential becomes infinite
and
when applying the matching condition. For an infinite well,
the points xmin,xmax are the ones where the potential becomes infinite
and  .
.
- Choose the initial value of the energy
 and of the energy variation
step
and of the energy variation
step  .
.
- Calculate xm from the initial value of the energy and the solution of
 . Choose the solution that is at the left most side .
. Choose the solution that is at the left most side .
- Evolve the equations (10.24) from xmin to xm and obtain the solutions
 ,
, .
.
- Evolve the equations (10.24) from xmax to xm and obtain the solutions
 ,
, .
.
- Renormalize
 , so that
, so that
 .
.
- Compute the ratio
 of equation (10.28) .
of equation (10.28) .
- If
 for appropriately chosen
for appropriately chosen  , the calculation ends.
The result for the energy eigenvalue and eigenfunction is considered to
be determined with adequate accuracy and we may proceed with the
analysis of the results.
, the calculation ends.
The result for the energy eigenvalue and eigenfunction is considered to
be determined with adequate accuracy and we may proceed with the
analysis of the results.
- If
 changes sign it means that we have crossed the energy
eigenvalue. Reverse the direction of search by taking
changes sign it means that we have crossed the energy
eigenvalue. Reverse the direction of search by taking  .
.
- Change the energy
 and repeat by going back to the fourth
step.
and repeat by going back to the fourth
step.
When we exit the above loop, the current wave function is a good approximation to
the eigenfunction  corresponding to the eigenvalue
corresponding to the eigenvalue  . We normalize the
wave function according to equation (10.2) and we calculate the expectation
values according to (10.9) . It is also interesting to determine the number of
nodes
. We normalize the
wave function according to equation (10.2) and we calculate the expectation
values according to (10.9) . It is also interesting to determine the number of
nodes
 of the wave function which is related to
of the wave function which is related to  by
by  .
.
Our program needs to implement the Runge–Kutta algorithm. We use the
routine RKSTEP (see page 539) which performs a 4th order Runge–Kutta step. Its
code is copied to the file rk.f90.
The potential  is coded in the function V(x). The boundary conditions
are programmed in the subroutine boundary(xmin, xmax, psixmin, psipxmin,
psixmax, psipxmax) which returns the values of psixmin =
is coded in the function V(x). The boundary conditions
are programmed in the subroutine boundary(xmin, xmax, psixmin, psipxmin,
psixmax, psipxmax) which returns the values of psixmin =  ,
psipxmin =
,
psipxmin =  , psixmax =
, psixmax =  , psipxmax =
, psipxmax =  to the calling program. These routines are put in a separate file for each
potential that we want to study. The name of the file is related to the form
of the potential, e.g. we choose schInfSq.f90 for the infinite potential
well of (10.17) . The same file contains the code for the functions f1,
f2:
to the calling program. These routines are put in a separate file for each
potential that we want to study. The name of the file is related to the form
of the potential, e.g. we choose schInfSq.f90 for the infinite potential
well of (10.17) . The same file contains the code for the functions f1,
f2:
!===========================================================
!file: schInfSq.f
!
!Functions used in RKSTEP routine. Here:
!f1 = psip(x) = psi(x)’
!f2 = psip(x)’= psi(x)’’
!
!One has to set:
! 1. V(x), the potential
! 2. The boundary conditions for psi,psip at x=xmin and x=xmax
!
!===========================================================
!----- potential:
real(8) function V(x)
implicit none
real(8) :: x
V = 0.0D0
end function V
!----- boundary conditions:
subroutine &
boundary(xmin,xmax,psixmin,psipxmin,psixmax,psipxmax)
implicit none
real(8) :: xmin,xmax,psixmin,psipxmin,psixmax,psipxmax,V
!for infinite square well we set psi=0 at boundary
!and psip=+/-1
psixmin = 0.0D0
psipxmin = 1.0D0
psixmax = 0.0D0
psipxmax = -1.0D0
!----- Initial values at xmin and xmax
end subroutine boundary
!===========================================================
!===========================================================
!----- trivial function: derivative of psi
real(8) function f1(x,psi,psip)
real(8) :: x,psi,psip
f1=psip
end function f1
!===========================================================
!----- the second derivative of wavefunction:
!psip(x)’ = psi(x)’’ = -(E-V) psi(x)
real(8) function f2(x,psi,psip)
implicit none
real(8) :: x,psi,psip,energy,V
common /params/energy
!----- Schroedinger eq: RHS
f2 = (V(x)-energy)*psi
end function f2
!===========================================================
We note that if the potential becomes infinite for  xmin and/or
xmin and/or  xmax,
then this will be determined by the boundary conditions at xmin and/or
xmax.
xmax,
then this will be determined by the boundary conditions at xmin and/or
xmax.
The main program is in the file sch.f90. The code is listed below and it
includes the function integrate(psi, dx, Nx) used for the normalization of the
wave function. It performs a numerical integration of the square of a function
whose values psi(i) i=1,...,Nx are given at an odd number of Nx equally
spaced points by a distance dx using Simpson’s rule.
!===========================================================
!
! File: sch.f90
!
! Integrate 1d Schrodinger equation from xmin to xmax.
! Determine energy eigenvalue and eigenfunction by matching
! evolving solutions from xmin and from xmax at a point xm.
! Matching done by equating values of functions and their
! derivatives at xm. The point xm chosen at the left most
! turning point of the potential at any given value of the
! energy. The potential and boundary conditions chosen in
! different file.
! ----------------------------------------------------------
! Input: energy: Trial value of energy
! de: energy step, if matching fails de -> e+de, if
! logderivative changes sign de -> -de/2
! xmin, xmax, Nx
! ----------------------------------------------------------
! Output: Final value of energy, number of nodes of
! wavefunction in stdout
! Final eigenfunction in file psi.dat
! All trial functions and energies in file all.dat
!===========================================================
program schroedinger_equation_1D
implicit none
integer,parameter :: P=20001
integer :: Nx,NxL,NxR
real(8) :: psi(P),psip(P)
real(8) :: dx
real(8) :: xmin,xmax,xm !left/right/matching points
real(8) :: psixmin,psipxmin,psixmax,psipxmax
real(8) :: psileft ,psiright ,psistep,psinorm
real(8) :: psipleft,psipright,psipstep
real(8) :: energy,de,epsilon,integrate
common/params/energy
real(8) :: matchlogd,matchold,psiold,norm,x
integer :: iter,i,imatch,nodes
real(8) :: V
!---------- Input:
print *,’# Enter energy,de,xmin,xmax,Nx’
read *,energy,de,xmin,xmax,Nx
!--- need even intervals for normalization integration
if( mod(Nx,2).eq.0)Nx=Nx+1
if( Nx .gt. P ) stop ’Fatal Error: Nx>P’
if( xmin .ge. xmax) stop ’Error: xmin >= xmax’
dx = (xmax - xmin)/(Nx-1)
epsilon = 1.0D-6
call boundary(xmin,xmax,psixmin,psipxmin,psixmax,psipxmax)
print *,’# #######################################’
print *,’# Estart= ’,energy, ’ de= ’,de
print *,’# Nx= ’,Nx ,’ eps= ’,epsilon
print *,’# xmin= ’,xmin,’ xmax= ’,xmax, ’ dx= ’,dx
print *,’# psi(xmin)= ’,psixmin,’ psip(xmin)= ’,psipxmin
print *,’# psi(xmax)= ’,psixmax,’ psip(xmax)= ’,psipxmax
print *,’# #######################################’
!----- Calculate:
open(unit=11,file=’all.dat’)
matchold = 0.0d0
do iter=1,10000
!----- Determine matching point at turning point from the left:
imatch = -1
do i=1,Nx
x = xmin + (i-1)*dx
if( imatch .lt. 0 .and. (energy-V(x)) .gt. 0.0D0) imatch = i
enddo
if( imatch .le. 100 .or. imatch .ge. Nx-100) imatch = Nx/5
xm = xmin + (imatch-1)*dx
NxL = imatch
NxR = Nx-imatch+1
!----- Evolve wavefunction from the left:
psi (1) = psixmin
psip (1) = psipxmin
psistep = psixmin
psipstep = psipxmin
do i=2,NxL
x = xmin + (i-2)*dx !this is x before the step
call RKSTEP(x,psistep,psipstep, dx)
psi (i) = psistep
psip(i) = psipstep
enddo
! use this to normalize eigenfunction to match at xm
psinorm = psistep
psipleft = psipstep
!----- Evolve wavefunction from the right:
psi (Nx) = psixmax
psip(Nx) = psipxmax
psistep = psixmax
psipstep = psipxmax
do i=2,NxR
x = xmax - (i-2)*dx
call RKSTEP(x,psistep,psipstep,-dx)
psi (Nx-i+1) = psistep
psip(Nx-i+1) = psipstep
enddo
psinorm = psistep/psinorm
psipright = psipstep
!----- Renormalize psil so that psil(xm)=psir(xm)
do i=1,NxL-1
psi (i) = psinorm * psi (i)
psip(i) = psinorm * psip(i)
enddo
psipleft = psinorm * psipleft
!----- print current solution:
do i=1,Nx
x = xmin + (i-1)*dx
write(11,*)iter,energy,x,psi(i),psip(i)
enddo
!----- matching using derivatives:
!Careful: this can fail if psi’(xm) = 0 !! (use also |de|<1e-6
!criterion)
matchlogd = &
(psipright-psipleft)/(DABS(psipright)+DABS(psipleft))
print *,’# iter,energy,de,xm,logd: ’,&
iter,energy,de,xm,matchlogd
!----- Exit condition:
if(DABS(matchlogd).le.epsilon.or.DABS(de/energy).lt.1.0D-12)&
EXIT
if( matchlogd * matchold .lt. 0.0D0) de = -0.5D0*de
energy = energy + de
matchold = matchlogd
enddo ! do iter=1,10000
close(11)
!---------------------------------------------------
!----- Solution has been found and now it is stored:
norm = integrate(psi,dx,Nx)
norm = 1.0D0/sqrt(norm)
do i=1,Nx
psi(i) = norm*psi(i)
enddo
!----- Cound number of zeroes, add one and get energy level:
nodes = 1
psiold = psi(1)
do i=2,Nx-1
!should be 0 within epsilon
if( DABS(psi(i)) .gt.epsilon)then
if( psiold*psi(i).lt.0.0D0 )nodes = nodes+1
psiold = psi(i)
endif
enddo !i=2,Nx-1
!------- Print final solution:
open(unit=11,file=’psi.dat’)
print *,’Final result: E= ’,energy,’ n= ’,nodes,&
’ norm = ’ ,norm
if( DABS(matchlogd) .gt. epsilon) print *&
,’Final result: SOS: logd>epsilon. logd= ’,matchlogd
write(11,*)’# E= ’ ,energy,’ n= ’,nodes,&
’ norm = ’ ,norm
do i=1,Nx
x = xmin + (i-1)*dx
write(11,*) x,psi(i)
enddo
close(11)
end program schroedinger_equation_1D
!===========================================================
!Simpson’s rule to integrate psi(x)*psi(x) for proper
!normalization. For n intervals of width dx (n even)
!Simpson’s rule is:
!int(f(x)dx) =
! (dx/3)*(f(x_0)+4 f(x_1)+2 f(x_2)+...+4 f(x_{n-1})+f(x_n))
!
!Input: Discrete values of function psi(Nx)
! Integration step dx
!Returns: Integral(psi(x)psi(x) dx)
!===========================================================
real(8) function integrate(psi,dx,Nx)
implicit none
integer :: Nx
!------------- Note: we need P due to geometry of array
real(8) :: psi(Nx),dx
!-------------
real(8) :: int
integer :: i
!----- zeroth order point:
i = 1
int = psi(i)*psi(i)
!----- odd order points (i=k+1 is even):
do i=2,Nx-1,2
int = int + 4.0D0*psi(i)*psi(i)
enddo
!----- even order points:
do i=3,Nx-2,2
int = int + 2.0D0*psi(i)*psi(i)
enddo
!----- last point:
i = Nx
int = int + psi(i)*psi(i)
!----- measure normalization:
int = int*dx/3.0D0
!----- final result:
integrate = int
end function integrate
!===========================================================
The reproduction of the results of the previous section for the infinite potential
well is left as an exercise. The compilation and running of the program can be
done with the commands:
> gfortran sch.f90 schInfSq.f90 rk.f90 -o s
> ./s
# Enter energy,de,xmin,xmax,Nx
1 0.5 -1 1 2000
# #######################################
# Estart= 1.000 de= 0.5
# Nx= 2001 eps= 1.0E-006
# xmin= -1.000 xmax= 1.000 dx= 1.000E-003
# psi(xmin)= 0.000 psip(xmin)= 1.000
# psi(xmax)= 0.000 psip(xmax)= -1.000
# #######################################
# iter,energy,de,xm,logd: 1 1.0000 0.500 -0.601 -0.9748
# iter,energy,de,xm,logd: 2 1.5000 0.500 -0.601 -0.6412
.....
# iter,energy,de,xm,logd: 30 2.4674 -3.815E-6 -0.601 -1.0E-6
# iter,energy,de,xm,logd: 31 2.4674 1.907E-6 -0.601 2.7E-7
Final result: E= 2.467401504516602 n= 1 norm = 1.5707965025
We set xmin= -1, xmax = 1, Nx= 2000 and  ,
,  . The energy of
the ground state is found to be
. The energy of
the ground state is found to be  . The wave
function is stored in the file psi.dat and can be plotted with the gnuplot
command
. The wave
function is stored in the file psi.dat and can be plotted with the gnuplot
command
gnuplot> plot "psi.dat" using 1:2 with lines
The functions computed during the iterations of the algorithm are stored in
the file all.dat. The first column is the iteration number (here we have iter =
0, ... 31) and we can easily filter each one of them with the commands
gnuplot> plot "<awk ’$1==1’ all.dat" using 3:4 w l t "iter=1"
gnuplot> replot "<awk ’$1==2’ all.dat" using 3:4 w l t "iter=2"
gnuplot> replot "<awk ’$1==3’ all.dat" using 3:4 w l t "iter=3"
gnuplot> replot "<awk ’$1==4’ all.dat" using 3:4 w l t "iter=4"
.....
which reproduce figure 10.6.
10.4 Measurements
The action of an operator  on a state
on a state  can be easily calculated in the
position representation by its action on the corresponding wave function
can be easily calculated in the
position representation by its action on the corresponding wave function  .
The action of the operators
.
The action of the operators
 | (10.29) |
yield
 | (10.30) |
Using equation (10.9) we can calculate the expectation value  of the
operator
of the
operator  when the system is at the state
when the system is at the state  . Interesting examples are the
observables “position”
. Interesting examples are the
observables “position”  , “position squared”
, “position squared”  , “momentum”
, “momentum”  , “momentum
squared”
, “momentum
squared”  , “kinetic energy”
, “kinetic energy”  , “potential energy”
, “potential energy”  , “energy” or
“Hamiltonian”
, “energy” or
“Hamiltonian”  whose expectation values are given by the relations
whose expectation values are given by the relations
We remind the reader that we used the dimensionless  as well as
equations (10.15) and (10.16) . Especially interesting are the “uncertainties”
as well as
equations (10.15) and (10.16) . Especially interesting are the “uncertainties”
 ,
,  that satisfy the inequality (“Heisenberg’s
uncertainty relation”)
that satisfy the inequality (“Heisenberg’s
uncertainty relation”)
 | (10.32) |
In the previous section we described how to calculate numerically the
eigenfunctions of the Hamiltonian. If  , we obtain that
, we obtain that
 . Other operators need a numerical approximation
for the calculation of their expectation values. If the values of the wave
function are given at
. Other operators need a numerical approximation
for the calculation of their expectation values. If the values of the wave
function are given at  equally spaced points
equally spaced points  , then we
obtain
, then we
obtain
 | (10.33) |
where  and
and
 | (10.34) |
Both equations entail an error of the order of  . Special care should be taken at
the endpoints of the interval
. Special care should be taken at
the endpoints of the interval ![[x ,x ]
1 N](main_latex3831x.png) . As a first approach we will use the naive
approximations
. As a first approach we will use the naive
approximations
and The relevant program that calculates  ,
,  ,
,  ,
,  ,
,  ,
,  can be
found in the file observables.f90 and is listed below:
can be
found in the file observables.f90 and is listed below:
!===========================================================
!
! File observables.f90
! Compile: gfortran observables.f90 -o o
! Usage: ./o <psi.dat>
!
! Read in a file with a wavefunction in the format of psi.dat:
! # E= <energy> ....
! x1 psi(x1)
! x2 psi(x2)
! ............
!
! Outputs expectation values:
! normalization Energy <x> <p> <x^2> <p^2> Dx Dp DxDp
! where Dx = sqrt(<x^2>-<x>^2) Dp = sqrt(<p^2>-<p>^2)
! DxDp = Dx * Dp
!
!===========================================================
program observables_expectation
implicit none
integer,parameter :: P=50000
integer Nx,i
real(8) :: xstep(P),psi(P),obs(P)
real(8) :: xav, pav, x2av, p2av, Dx, Dp, DxDp,energy,h,norm
real(8) :: integrate
character(20) :: psifile,scratch
!the first argument of the command line must be the path
!to the file with the wavefunction. (GNU fortran extension...)
if( iargc() .ne. 1) stop ’Usage: o <filename>’
call getarg(1,psifile)
!If the file does not exist, we go to label 100 (stop):
open(unit=11,file=psifile,status=’OLD’,err=100)
print *,"# reading wavefunction from file:", psifile
!we read the first comment line from the file:
read(11,*) scratch,scratch,energy
!-------------------------------------------------------
!Input data: psi(x)
Nx = 1
do while(.TRUE.)
if(Nx .ge. P) stop ’Too many points’
read(11,*,end=101) xstep(Nx),psi(Nx)
Nx = Nx+1
enddo !do while(.TRUE.)
101 continue
Nx = Nx - 1
if(mod(Nx,2) .eq. 0) Nx = Nx - 1
h = (xstep(Nx)-xstep(1))/(Nx-1)
!-------------------------------------------------------
!Calculate:
!---------- norm:
do i=1,Nx
obs(i) = psi(i)*psi(i)
enddo
norm = integrate(obs,h,Nx)
!---------- <x> :
do i=1,Nx
obs(i) = xstep(i)*psi(i)*psi(i)
enddo
xav = integrate(obs,h,Nx)/norm
!---------- <p>/i :
obs(1) = psi(1)*(psi(2)-psi(1))/h
do i=2,Nx-1
obs(i) = psi(i)*(psi(i+1)-psi(i-1))/(2.0D0*h)
enddo
obs(Nx) = psi(Nx)*(psi(Nx)-psi(Nx-1))/h
pav = -integrate(obs,h,Nx)/norm
!--------- <x^2>
do i=1,Nx
obs(i) = xstep(i)*xstep(i)*psi(i)*psi(i)
enddo
x2av = integrate(obs,h,Nx)/norm
!-------- <p^2>
obs(1) = psi(1)*(psi(3)-2.0D0*psi(2)+psi(1))/(h*h)
do i=2,Nx-1
obs(i) = psi(i)*(psi(i+1)-2.0D0*psi(i)+psi(i-1))/(h*h)
enddo
obs(Nx) = psi(Nx)*&
(psi(Nx)-2.0D0*psi(Nx-1)+psi(Nx-2))/(h*h)
p2av = -integrate(obs,h,Nx)/norm
!-------- Dx
Dx = sqrt(x2av - xav*xav)
!-------- Dp
Dp = sqrt(p2av - pav*pav)
!-------- Dx . Dp
DxDp = Dx*Dp
!print results:
print *,’# norm E <x> <p>/i <x^2> <p^2> Dx Dp DxDp’
print ’(10G25.17)’,norm,energy,xav,pav,x2av,p2av,Dx,Dp,DxDp
stop !normal execution ends here. Error messages follow
100 stop ’Cannot open file’
end program observables_expectation
!===========================================================
!
!Simpson’s rule to integrate psi(x).
!For n intervals of width dx (n even)
!Simpson’s rule is:
!int(f(x)dx) =
! (dx/3)*(f(x_0)+4 f(x_1)+2 f(x_2)+...+4 f(x_{n-1})+f(x_n))
!
!Input: Discrete values of function psi(Nx)
! Integration step dx
!Returns: Integral(psi(x)psi(x) dx)
!===========================================================
real(8) function integrate(psi,dx,Nx)
implicit none
integer :: Nx
real(8) :: psi(Nx),dx
real(8) :: int
integer i
!----- zeroth order point:
i = 1
int = psi(i)
!----- odd order points (i=k+1 is even):
do i=2,Nx-1,2
int = int + 4.0D0*psi(i)
enddo
!----- even order points:
do i=3,Nx-2,2
int = int + 2.0D0*psi(i)
enddo
!----- last point:
i = Nx
int = int + psi(i)
!----- measure normalization:
int = int*dx/3.0D0
!----- final result:
integrate = int
end function integrate
!===========================================================
The program needs to read in the wave function at the points  in the
format produced by the program in sch.f90. The first line should have the energy
written at the 3rd column, whereas from the 2nd line and on there should be two
columns with the
in the
format produced by the program in sch.f90. The first line should have the energy
written at the 3rd column, whereas from the 2nd line and on there should be two
columns with the  pairs. It is not necessary to have the wave
function properly normalized, the program will take care of it. If this data is
stored in a file psi.dat, then the program can be used by running the
commands
pairs. It is not necessary to have the wave
function properly normalized, the program will take care of it. If this data is
stored in a file psi.dat, then the program can be used by running the
commands
> gfortran observables.f90 -o obs
> ./obs psi.dat
The program prints the normalization constant of  , the value of the
energy ,
, the value of the
energy ,
 ,
,  ,
,  ,
,  ,
,  ,
,  and
and  to the stdout.
to the stdout.
Some details about the program: In order to read in the data from the file
psi.dat we use the functions iargc(), getarg(n,string). The former
returns the number of arguments of the command line and the latter
stores the n-th argument to the CHARACTER variable string. Therefore, the
statements
character(20) :: psifile,scratch
if( iargc() .ne. 1) stop ’Usage: o <filename>’
call getarg(1,psifile)
stop the program if the command line does not have exactly one argument and
store the first argument to the variable file.
The command
open(unit=11,file=psifile,status=’OLD’,err=100)
100 stop ’Cannot open file’
opens a file which should already exist (status=’OLD’), otherwise an
error message is issued. The option err=100 transfers the control of the
program to the statement labeled ’100’. In the example shown above, the
program stops and prints an error message ’Cannot open filename’ to the
stdout.
The commands
Nx = 1
do while(.TRUE.)
read(11,*,end=101) xstep(Nx),psi(Nx)
Nx = Nx+1
enddo !do while(.TRUE.)
101 continue
read the opened file line by line. The option end=101 at the statement
read(11,*,end=101) transfers the control of the program to the labeled
statement with label 101 (i.e. outside the do loop) when we reach the end of
file.
The rest of the commands are applications of equations (10.33) , (10.34) ,
(10.35) and (10.36) to the formulas (10.31) and the reader is asked to study
them carefully. The program uses the function integrate in order to perform the
necessary integrals.
10.5 The Anharmonic Oscillator - Again...
In the previous chapter 9 we studied the quantum mechanical harmonic and
anharmonic oscillator in the representation of the energy eigenstates of the
harmonic oscillator  . In this section we will revisit the problem by using the
position representation. We will calculate the eigenfunctions
. In this section we will revisit the problem by using the
position representation. We will calculate the eigenfunctions  that
diagonalize the Hamiltonian (9.15) , which are the solutions of the Schrödinger
equation. By setting
that
diagonalize the Hamiltonian (9.15) , which are the solutions of the Schrödinger
equation. By setting  in equation (10.13) , equation (10.12)
becomes
in equation (10.13) , equation (10.12)
becomes
 | (10.37) |
where  . For
. For  we obtain the harmonic oscillator with
we obtain the harmonic oscillator with
 | (10.38) |
where  are the Hermite polynomials.
are the Hermite polynomials.
We start with the simple harmonic oscillator where the exact solution is
known. The potential and the initial conditions are programmed in the file
schHOC.f90. The changes that we need to make concern the functions V(x),
boundary(xmin, xmax, psixmin, psipxmin, psixmax, psipxmax):
!===========================================================
!file: schHOC.f
!..............
!----- potential:
real(8) function V(x)
implicit none
real(8) :: x
V = x*x
end function V
!----- boundary conditions:
subroutine &
boundary(xmin,xmax,psixmin,psipxmin,psixmax,psipxmax)
implicit none
real(8) :: xmin,xmax,psixmin,psipxmin,psixmax,psipxmax,V
psixmin = exp(-0.5D0*xmin*xmin)
psipxmin = -xmin*psixmin
psixmax = exp(-0.5D0*xmax*xmax)
psipxmax = -xmax*psixmax
end subroutine boundary
!===========================================================
.................
The code omitted at the dots is identical to the one discussed in the previous section.
The initial conditions are inspired by the asymptotic behavior of the solutions to
Schrödinger’s
equation  ,
,  . You are encouraged to test the
influence of other choices on the results.
. You are encouraged to test the
influence of other choices on the results.
The results are depicted in figure 10.7 where, besides the qualitative
agreement, their difference from the known values (10.38) is also shown. This
difference turns out to be of the order of  –
– . The values of the energy
. The values of the energy
 for
for  are in agreement with (10.38) with relative accuracy better than
are in agreement with (10.38) with relative accuracy better than
 .
.
Then we calculate the expectation values  ,
,  ,
,  ,
,  ,
,  and
and
 . These are easily calculated using equations (9.4) and (9.8) . We
see that
. These are easily calculated using equations (9.4) and (9.8) . We
see that  ,
,  ,
whereas
,
whereas
 | (10.39) |
The program observables.f90 calculates  with accuracy
with accuracy  and
and
 with accuracy
with accuracy  . The expectation values
. The expectation values  ,
,  are shown
in table 10.2.
are shown
in table 10.2.
Next, the calculation is repeated for the anharmonic oscillator for
 . We copy the file schHOC.f90 to schUOC.f90 and change the
potential in the function V(x):
. We copy the file schHOC.f90 to schUOC.f90 and change the
potential in the function V(x):
!===========================================================
!file: schUOC.f
!...................
!----- potential:
real(8) function V(x)
implicit none
real(8) :: x, lambda
lambda = 2.0D0
V = x*x+2.0D0*lambda*x*x*x*x
end function V
....................
The wave functions are plotted in figure 10.8. We see that by increasing  the
particle becomes more confined in space as expected. In table 10.3 we list the
values of the energy
the
particle becomes more confined in space as expected. In table 10.3 we list the
values of the energy  for
for  . By increasing
. By increasing  ,
,  is increased.
Table 10.4 lists the expectation values
is increased.
Table 10.4 lists the expectation values  ,
,  and
and  for the
anharmonic oscillator for the states
for the
anharmonic oscillator for the states  ,
,  . By increasing
. By increasing  ,
,
 is decreased and
is decreased and  is increased. The product of the
uncertainties
is increased. The product of the
uncertainties  seems to be quite close to the corresponding values for the
harmonic oscillator. The results should be compared with the ones obtained in
table 9.1 of chapter 9.
seems to be quite close to the corresponding values for the
harmonic oscillator. The results should be compared with the ones obtained in
table 9.1 of chapter 9.
10.6 The Lennard–Jones Potential
The Lennard–Jones potential is a simple phenomenological model of the
interaction between two neutral atoms in a diatomic molecule. This is given
by
 | (10.40) |
The repulsive term describes the Pauli interaction due to the overlapping of the
electron orbitals, whereas the attractive term describes the Van der Waals force.
The first one dominates at short distances and the latter at long distances. We
choose  in (10.13) and define
in (10.13) and define  . Equation (10.40)
becomes
. Equation (10.40)
becomes
 | (10.41) |
whereas the eigenvalues  are related to the energy values
are related to the energy values  by
by
 | (10.42) |
The plot of the potential is shown in figure 10.5 for  . The minimum is
located at
. The minimum is
located at  and its value is
and its value is  . The code for this
potential is in the file schLJ.f90. The necessary changes to the code discussed in
the previous sections are listed below:
. The code for this
potential is in the file schLJ.f90. The necessary changes to the code discussed in
the previous sections are listed below:
!===========================================================
!file: schLJ.f90 (Lennard-Jones)
!..................
!----- potential:
real(8) function V(x)
implicit none
real(8) :: x,V0
V0 = 250.0D0
V = 4.0D0*V0*(1.0D0/x**12-1.0D0/x**6)
end function V
!----- boundary conditions:
subroutine &
boundary(xmin,xmax,psixmin,psipxmin,psixmax,psipxmax)
implicit none
real(8) :: xmin,xmax,psixmin,psipxmin,psixmax,psipxmax,V
real(8) :: energy
common/params/energy
!----- Initial values at xmin and xmax
psixmin = exp(-xmin*sqrt(DABS(energy-V(xmin))))
psipxmin = sqrt(DABS(energy-V(xmin)))*psixmin
psixmax = exp(-xmax*sqrt(DABS(energy-V(xmax))))
psipxmax = -sqrt(DABS(energy-V(xmax)))*psixmax
end subroutine boundary
............................
|
|
|
|
|
|
|
|
|
| | | | | | | |
|
|
|
|
|
|
|
|
|
|
| 0 | -173.637 | 1.186 | 1.0e-10 | 1.415 | 34.193 | 0.091 | 5.847 | 0.534 |
| 1 | -70.069 | 1.364 | 6.0e-11 | 1.893 | 56.832 | 0.178 | 7.539 | 1.338 |
| 2 | -18.191 | 1.699 | -4.5e-08 | 2.971 | 39.480 | 0.291 | 6.283 | 1.826 |
| 3 | -1.317 | 2.679 | -2.6e-08 | 7.586 | 9.985 | 0.638 | 3.160 | 2.016 |
|
|
|
|
|
|
|
|
|
| |
Table 10.5: The results for the Lennard-Jones potential with  . We find 4
bound states.
. We find 4
bound states.
For the integration we choose  and xmin = 0.7,
and xmin = 0.7,  xmax
xmax  .
The results are plotted in figure 10.9. There are four bound states. The first
two ones are quite confined within the potential well whereas the last
ones begin to “spill” out of it. Table 10.5 lists the results. We observe
that
.
The results are plotted in figure 10.9. There are four bound states. The first
two ones are quite confined within the potential well whereas the last
ones begin to “spill” out of it. Table 10.5 lists the results. We observe
that  within the attained accuracy as expected for real, bound
states .
within the attained accuracy as expected for real, bound
states .
10.7 Problems
- Add the necessary code to the program in the file well.f90 so that the
final wave function printed in the file psi.dat is properly normalized. The
integral
 can be computed using the Simpson rule
The interval
can be computed using the Simpson rule
The interval ![[a,b]](main_latex3986x.png) is discretized by
is discretized by  points
points  where
where  is even. Each interval
is even. Each interval ![[x ,x ]
i i+1](main_latex3990x.png) has width
has width  .
.
- Add the necessary code to the program in the file well.f90 in order to
calculate the number of nodes (zeroes) of the wave function. Using this
result, the program should print the level
 of the calculated wave function
of the calculated wave function
 .
.
- Calculate the wave functions of the energy eigenstates for the potential
(10.27) with
 . This is the problem of the (finite) potential well.
Solve the problem for
. This is the problem of the (finite) potential well.
Solve the problem for  and
and  . How many bound states do
you find? Next study the influence of the wall on the solutions. Introduce a
parameter
. How many bound states do
you find? Next study the influence of the wall on the solutions. Introduce a
parameter  so that
so that  and study the dependence of the
solutions on
and study the dependence of the
solutions on  . Take
. Take  and
compute the difference of the first two energy eigenvalues. Estimate the
accuracy of the method. Next lower the value of
and
compute the difference of the first two energy eigenvalues. Estimate the
accuracy of the method. Next lower the value of  until there is no
bound state. What is the relation between
until there is no
bound state. What is the relation between  and
and  when this happens?
Compare with the analytic result which you know from your quantum
mechanics course.
when this happens?
Compare with the analytic result which you know from your quantum
mechanics course.
Hint: For the largest values of  , take Nx > 1000. When convergence is not
achieved decrease epsilon.
, take Nx > 1000. When convergence is not
achieved decrease epsilon.
- Set
 to the double well potential. Observe the (almost)
degenerate states and plot the wave functions
to the double well potential. Observe the (almost)
degenerate states and plot the wave functions  ,
where
,
where  is odd. Compare the results with the corresponding energy levels
and eigenfunctions of the infinite square well. Increase
is odd. Compare the results with the corresponding energy levels
and eigenfunctions of the infinite square well. Increase  to the point
where you cannot solve the problem numerically.
to the point
where you cannot solve the problem numerically.
Hint: For large  the numerical effort is increased. For
the numerical effort is increased. For  the wave
function is almost zero and it is hard to obtain the non trivial wave function
for
the wave
function is almost zero and it is hard to obtain the non trivial wave function
for  . As the accuracy deteriorates, you should increase
epsilon in the program so that convergence is achieved relatively
fast.
. As the accuracy deteriorates, you should increase
epsilon in the program so that convergence is achieved relatively
fast.
- Repeat problems 3 and 4 using the program sch.f90. Compare the
results.
- Study the bound states in the potentials
 for
for  and
and
 for
for  and
and
 for
for  . In each case
calculate
. In each case
calculate  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
- Write a program that calculates the probability that a particle is
found in an interval
![[x1,x2]](main_latex4025x.png) given the wave function calculated
by the program in the file sch.f90. Apply your program on the
results of the previous problem and calculate the intervals
given the wave function calculated
by the program in the file sch.f90. Apply your program on the
results of the previous problem and calculate the intervals ![[− x1,x1]](main_latex4026x.png) where the probability to find the particle inside them is equal to
where the probability to find the particle inside them is equal to
 .
.
- Fill the tables 10.3 and 10.4 with the results for
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  and plot each expectation value as a function of
and plot each expectation value as a function of
 .
.
- A particle is under the influence of a potential
 The energy spectrum is given by
The energy spectrum is given by
 for the values of
for the values of  for which
for which  . Calculate the
energy levels
. Calculate the
energy levels  of the bound states numerically by setting
of the bound states numerically by setting  in
equation (10.13) and
in
equation (10.13) and  . Plot the potential
. Plot the potential  and the
corresponding eigenfunctions. Calculate the expectation values of the
position and momentum, the uncertainties in position and momentum and
their product. Repeat for
and the
corresponding eigenfunctions. Calculate the expectation values of the
position and momentum, the uncertainties in position and momentum and
their product. Repeat for  .
.
- Write a program that reads in a wavefunction and calculates the
expectation value of the Hamiltonian
 by assuming that
by assuming that  is real. Calculate
is real. Calculate  for the harmonic
oscillator for
for the harmonic
oscillator for  and show (numerically) that
and show (numerically) that  .
.
- Consider a particle in the Morse potential
 Calculate the energy spectrum of the bound states. Choose
Calculate the energy spectrum of the bound states. Choose  ,
,
 ,
,  ,
,  and obtain
and obtain
 Compare your results with the known analytic solutions
Compare your results with the known analytic solutions

 where
where  ,
,  , and
, and
 is a Laguerre polynomial given by
is a Laguerre polynomial given by 
 . You can take
. You can take
 ,
,  and calculate
and calculate  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 .
.
- Calculate the wave functions of the eigenstates of the Hamiltonian for the
anharmonic oscillator for
 and
and  . Calculate the
wavefunctions using the program anharmonic.f90 of chapter 9 for
. Calculate the
wavefunctions using the program anharmonic.f90 of chapter 9 for
 and compare the two results.
and compare the two results.
Hint: Write a program that calculates the energy eigenfunctions of the
simple harmonic oscillator
 where the Hermite polynomials satisfy the relations
where the Hermite polynomials satisfy the relations
 The program anharmonic.f90 calculates the eigenstates of the anharmonic
oscillator
The program anharmonic.f90 calculates the eigenstates of the anharmonic
oscillator
 by storing the coefficients of the linear expansion in the elements of the
array H(N,N). The same relation holds for the corresponding wave functions
by storing the coefficients of the linear expansion in the elements of the
array H(N,N). The same relation holds for the corresponding wave functions
 ,
,  . From
. From  and H(i,j) calculate
and H(i,j) calculate  for
for
 and determine the accuracy achieved by the calculation for
each
and determine the accuracy achieved by the calculation for
each  . For which values of
. For which values of  do you obtain large discrepancies between
your results? Remember that for large
do you obtain large discrepancies between
your results? Remember that for large  , the states of high energy
contribute more than for small
, the states of high energy
contribute more than for small  . Figure 10.10 can help you understanding
this statement.
. Figure 10.10 can help you understanding
this statement.
Chapter 11
The Random Walker
In this chapter we will study the typical path followed by a ... drunk when he
decides to start walking from a given position. Because of his drunkenness, his
steps are in random directions and uncorrelated. These are the basic properties of
the models that we are going to study. These models are related to specific
physical problems like the Brownian motion, the diffusion, the motion of
impurities in a lattice, the large distance properties of macromolecules etc. In the
physics of elementary particles random walks describe the propagation of free
scalar particles and they most clearly arise in the Feynman path integral
formulation of the euclidean quantum field theory. Random walks are precursors
to the theory of random surfaces which is related to the theory of two dimensional
“soft matter” membranes, two dimensional quantum gravity and string theory
[44].
The geometry of a typical path of a simple random walk is not classical and this
can be seen from two of its non classical properties. First, the average distance
traveled by the random walker is proportional to the square root of the time
traveled, i.e. the classical relation  does not apply. Second, the geometry of
the path of the random walker has fractal dimension which is larger than
one .
Similar structures arise in the study of quantum field theories and random
surfaces, where the non classical properties of a typical configuration can be
described by appropriate generalizations of these concepts. For further study we
refer to [7, 43, 44, 45].
does not apply. Second, the geometry of
the path of the random walker has fractal dimension which is larger than
one .
Similar structures arise in the study of quantum field theories and random
surfaces, where the non classical properties of a typical configuration can be
described by appropriate generalizations of these concepts. For further study we
refer to [7, 43, 44, 45].
In order to simulate a stochastic system on the computer, it is necessary to use
random number generators. In most of the cases, these are deterministic
algorithms that generate a sequence of pseudorandom numbers distributed
according to a desired distribution. The heart of these algorithms generate
numbers distributed uniformly from which we can generate any other complex
distribution. In this chapter we will study simple random number generators and
learn how to use high quality, research grade, portable, random number
generators.
11.1 (Pseudo)Random Numbers
The production of pseudorandom
numbers is at the heart of a Monte Carlo simulation. The algorithm used in their
production is deterministic: The generator is put in an initial state and the
sequence of pseudorandom numbers is produced during its “time evolution”. The
next number in the sequence is determined from the current state of the generator
and it is in this sense that the generator is deterministic. Same initial
conditions result in exactly the same sequence of pseudorandom numbers. But
the “time evolution” is chaotic and “neighboring” initial states result
in very different, uncorrelated, sequences. The chaotic properties of the
generators is the key to the pseudorandomness of the numbers in the sequence:
the numbers in the sequence decorrelate exponentially fast with “time”.
But this is also the weak point of the pseudorandom number generators.
Bad generators introduce subtle correlations which produce systematic
errors. Truly random numbers (useful in cryptography) can be generated
by using special devices based on e.g. radioactive decay or atmospheric
noise .
Almost random numbers are produced by the special files /dev/random and
/dev/urandom available on unix systems, which read bits from an entropy pool
made up from several external sources (computer temperature, device noise
etc).
Pseudorandom number generators, however, are the source of random numbers
of choice when efficiency is important. The most popular generators are the
modulo generators (D.H. Lehmer, 1951) because of their simplicity. Their state is
determined by only one integer  from which the next one
from which the next one  is generated by
the relation
is generated by
the relation
 | (11.1) |
for appropriately chosen values of  ,
,  and
and  . In the bibliography, there is a
lot of discussion on the good and bad choices of
. In the bibliography, there is a
lot of discussion on the good and bad choices of  ,
,  and
and  , which
depend on the programming language and whether we are on a 32–bit
or 64–bit systems. For details see the chapter on random numbers in
[8].
, which
depend on the programming language and whether we are on a 32–bit
or 64–bit systems. For details see the chapter on random numbers in
[8].
The value of the integer  determines the maximum period of the sequence.
It is obvious that if the sequence encounters the same number after
determines the maximum period of the sequence.
It is obvious that if the sequence encounters the same number after  steps, then
the exact same sequence will be produced and
steps, then
the exact same sequence will be produced and  will be the period of the
sequence. Since there are at most
will be the period of the
sequence. Since there are at most  different numbers, the period is at most
equal to
different numbers, the period is at most
equal to  . For a bad choice of
. For a bad choice of  ,
,  and
and  the period will be much smaller.
But
the period will be much smaller.
But  cannot be arbitrarily large since there is a maximum number of bits that
computers use for the storage of integers. For 4-byte (32 bit) unsigned integers the
maximum number is
cannot be arbitrarily large since there is a maximum number of bits that
computers use for the storage of integers. For 4-byte (32 bit) unsigned integers the
maximum number is  , whereas for signed integers
, whereas for signed integers  . One can
prove
that a good choice of
. One can
prove
that a good choice of  ,
,  and
and  results in a sequence which is a permutation
results in a sequence which is a permutation
 of the numbers
of the numbers  . This is good enough for simple
applications that require fast random number generation but for serious
calculations one has to carefully balance efficiency with quality. Good quality
random generators are more complicated algorithms and their states are
determined by more than one integer. If you need the source code for such
generators you may look in the bibliography, like in e.g. [4], [5], [8],
[47]. If portability is an issue, we recommend the RANLUX random
number generator [47] or the Marsaglia, Zaman and Tsang generator.
The Fortran code for RANLUX can also be found in the accompanying
software, whereas the MZT generator can be found in Berg’s book/site [5].
. This is good enough for simple
applications that require fast random number generation but for serious
calculations one has to carefully balance efficiency with quality. Good quality
random generators are more complicated algorithms and their states are
determined by more than one integer. If you need the source code for such
generators you may look in the bibliography, like in e.g. [4], [5], [8],
[47]. If portability is an issue, we recommend the RANLUX random
number generator [47] or the Marsaglia, Zaman and Tsang generator.
The Fortran code for RANLUX can also be found in the accompanying
software, whereas the MZT generator can be found in Berg’s book/site [5].
In order to understand the use of random number generators, but also in order
to get a feeling of the problems that may arise, we list the code of the two
functions naiveran() and drandom(). The first one is obviously problematic and
we will use it in order to study certain type of correlations that may exist in
the generated sequences of random numbers. The second one is much
better and can be used in non–trivial applications, like in the random
walk generation or in the Ising model simulations studied in the following
chapters.
The function naiveran() is a simple application of equation (11.1) with
 ,
,  and
and  :
:
!=============================================
!File: naiveran.f90
!Program to demonstrate the usage of a modulo
!generator with a bad choice of constants
!resulting in strong pair correlations between
!generated numbers
!=============================================
real(8) function naiveran()
implicit none
integer :: iran=13337
common /naiveranpar/ iran
integer,parameter :: m = 131072 ! equal to 2**17
integer,parameter :: a = 1277
iran = a*iran
iran = MOD(iran,m)
naiveran = iran/DBLE(m)
end function naiveran
The function drandom() is also an application of the same equation,
but now we set  ,
,  and
and  . This is the choice of
Lewis, Goodman and Miller (1969) and provides a generator that passes
many tests and, more importantly, it has been used countless of times
successfully. One technical problem is that, when we multiply
. This is the choice of
Lewis, Goodman and Miller (1969) and provides a generator that passes
many tests and, more importantly, it has been used countless of times
successfully. One technical problem is that, when we multiply  by
by  ,
we may obtain a number which is outside the range of 4-byte integers
and this will result in an “integer overflow”. In order to have a fast and
portable code, it is desirable to stay within the range of the
,
we may obtain a number which is outside the range of 4-byte integers
and this will result in an “integer overflow”. In order to have a fast and
portable code, it is desirable to stay within the range of the  positive, 32-bit (4 byte), signed integers. Schrage has proposed to use the
relation
positive, 32-bit (4 byte), signed integers. Schrage has proposed to use the
relation
![( [ ]
|| a (xi− 1 modq ) − r xi−1- if it is ≥ 0
{ [ q ]
(axi−1) modm = | a (xi− 1 modq ) − r xi−q1- + m if it is < 0
|(](main_latex4123x.png) | (11.2) |
where  ,
, ![q = [m ∕a ]](main_latex4125x.png) and
and  . One can show that if
. One can show that if
 and if
and if  , then
, then  ,
,
![0 ≤ r[xi−1∕q] ≤ m − 1](main_latex4130x.png) and that (11.2) is valid. The period of the generator is
and that (11.2) is valid. The period of the generator is
 . The proof of the above statements is left as an exercise to the
reader.
. The proof of the above statements is left as an exercise to the
reader.
!====================================================
!File: drandom.f90
!Implementation of the Schrage algorithm for a
!portable modulo generator for 32 bit signed integers
!(from numerical recipes)
!
!returns uniformly distributed pseudorandom numbers
! 0.0 < x < 1.0 (0 and 1 excluded)
!====================================================
real(8) function drandom()
implicit none
integer,parameter :: a = 16807 ! a = 7**5
integer,parameter :: m = 2147483647 ! m = a*q+r = 2**31-1
integer,parameter :: q = 127773 ! q = [m/a]
integer,parameter :: r = 2836 ! r = MOD(m,a)
real(8),parameter :: f = (1.0D0/m)
integer :: p
integer :: seed
real(8) :: dr
common /randoms/seed
101 continue
p = seed/q ! = [seed/q]
seed = a*(seed- q*p) - r*p ! = a*MOD(seed,q)-r*[seed/q]
if(seed .lt. 0) seed = seed + m
dr = f*seed
if( dr .le. 0.0D0 .or. dr .ge. 1.0D0) goto 101
drandom = dr
end function drandom
The line that checks the result produced by the generator is necessary in order
to check for the number  which appears once in the sequence. This
adds a
which appears once in the sequence. This
adds a  % overhead, depending on the compiler. If you don’t
care about that, you may remove the line. Note that the number seed
is put in a common block so it can be accessed by other parts of the
program.
% overhead, depending on the compiler. If you don’t
care about that, you may remove the line. Note that the number seed
is put in a common block so it can be accessed by other parts of the
program.
Now we will write a program in order to test the problem of correlations in the
sequence of numbers produced by naiveran(). The program will produce pairs of
integers  , where
, where  , which are subsequently mapped on
the plane. This is done by taking the integer part of the numbers
, which are subsequently mapped on
the plane. This is done by taking the integer part of the numbers  with
with  and
and  is the random number produced by the
generator:
is the random number produced by the
generator:
!==========================================================
!Program that produces N random points (i,j) with
!0<= i,j < 10000. Simple qualitative test of serial
!correlations of random number generators on the plane.
!
!compile:
!gfortran correlations2ran.f90 naiveran.f90 drandom.f90
!==========================================================
program correlations2
implicit none
integer,parameter :: L = 10000
integer :: i,N
character(10) :: arg
real(8) :: naiveran,drandom
integer :: seed
common /randoms/ seed
!Read the number of points from first command argument
if(IARGC() .EQ. 1)then
call GETARG(1,arg); read(arg,*)N !convert string->integer
else !default value, if no N given by user:
N=1000
endif
seed = 348325
do i=1,N
print *,INT(L * naiveran()),INT(L * naiveran())
! print *,INT(L * drandom ()),INT(L * drandom ())
enddo
end program correlations2
The program can be found in the file correlations2ran.f90. In order to test
naiveran() we compile with the command
> gfortran correlations2ran.f90 naiveran.f90 -o naiveran
whereas in order to test drandom() we uncomment the print lines as
follows
! print *,INT(L * naiveran()),INT(L * naiveran())
print *,INT(L * drandom ()),INT(L * drandom ())
and recompile:
> gfortran correlations2ran.f90 drandom.f90 -o drandom
These commands result in two executable files naiveran and drandom. In order
to see the results we run the commands
> ./naiveran 100000 > naiveran.out
> ./drandom 100000 > drandom.out
> gnuplot
gnuplot> plot "naiveran.out" using 1:2 with dots
gnuplot> plot "drandom.out" using 1:2 with dots
which produce  points used in the plots in figures 11.1 and 11.2. In the plot
of figure 11.1, we see the pair correlations between the numbers produced by
naiveran(). Figure 11.2 shows the points produced by drandom(), and we can
see that the correlations shown in figure 11.1 have vanished. The plot in figure
11.2 is qualitative, and a detailed, quantitative, study of drandom() shows that
the pairs
points used in the plots in figures 11.1 and 11.2. In the plot
of figure 11.1, we see the pair correlations between the numbers produced by
naiveran(). Figure 11.2 shows the points produced by drandom(), and we can
see that the correlations shown in figure 11.1 have vanished. The plot in figure
11.2 is qualitative, and a detailed, quantitative, study of drandom() shows that
the pairs  that it produces, do not pass the
that it produces, do not pass the  test when we have more
than
test when we have more
than  points, which is much less than the period of the generator. In order to
avoid such problems, there are many solutions that have been proposed and the
simplest among them “shuffle” the results so that the low order serial
correlations vanish. Such generators will be discussed in the next section.
points, which is much less than the period of the generator. In order to
avoid such problems, there are many solutions that have been proposed and the
simplest among them “shuffle” the results so that the low order serial
correlations vanish. Such generators will be discussed in the next section.
The uniform distribution of the random numbers produced
can be examined graphically by constructing a histogram of the
relative frequency of their appearance. In order to construct the
histograms we use the script histogram which is written in the awk
language
as shown below:
> histogram -v f=0.01 drandom.out > drandom.hst
> gnuplot
gnuplot> plot "drandom.hst" using 1:3 with histeps
gnuplot> plot [:][0:] "drandom.hst" using 1:3 with histeps
The command histogram -v f=0.01 constructs a histogram of the data so that
the bin width is  . The reciprocal of the number following the option
-v f=0.01 defines the bin width. The histogram is saved in the file drandom.out.
. The reciprocal of the number following the option
-v f=0.01 defines the bin width. The histogram is saved in the file drandom.out.
The results are shown in figures 11.3 and 11.4. Next, we study the variance of
the measurements, shown in figure 11.3. The variance is decreased with
the size of the sample of the collected random numbers. This is seen in
the histogram of figure 11.5. For a quantitative study of the dependence
of the variance on the size  of the sample, we calculate the standard
deviation
of the sample, we calculate the standard
deviation
 | (11.3) |
where  is the sequence of random numbers. Figure 11.6 plots this relation.
By fitting
is the sequence of random numbers. Figure 11.6 plots this relation.
By fitting
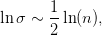 | (11.4) |
to a straight line, we see that
 | (11.5) |
If we need to generate random numbers which are distributed according to the
probability density  we can use a sequence of uniformly distributed random
numbers in the interval
we can use a sequence of uniformly distributed random
numbers in the interval  as follows: Consider the cumulative distribution
function
as follows: Consider the cumulative distribution
function
 | (11.6) |
which is equal to the area under the curve  in the interval
in the interval ![(− ∞, x]](main_latex4157x.png) and it
is equal to the probability
and it
is equal to the probability  . If
. If  is uniformly distributed in the
interval
is uniformly distributed in the
interval  then we have that
then we have that  . Therefore
. Therefore  is such
that
is such
that  and follows the
and follows the  distribution. Therefore, if
distribution. Therefore, if
 form a sequence of uniformly distributed random numbers, then the
numbers
form a sequence of uniformly distributed random numbers, then the
numbers
 | (11.7) |
form a sequence of random numbers distributed according to  .
.
Consider for example the Cauchy distribution
 | (11.8) |
Then
 | (11.9) |
According to the previous discussion, the random number generator is given by
the equation
 | (11.10) |
or equivalently (for a more efficient generation)
 | (11.11) |
The generator of Gaussian random numbers is found in many applications.
The Gaussian distribution is given by the probability density
 | (11.12) |
The cumulative distribution function is
 | (11.13) |
where  is the error function. The error function, as
well as its inverse, can be calculated numerically, but this would result in a slow
computation. A trick to make a more efficient calculation is to consider the
probability density
is the error function. The error function, as
well as its inverse, can be calculated numerically, but this would result in a slow
computation. A trick to make a more efficient calculation is to consider the
probability density  of two independent Gaussian random variables
of two independent Gaussian random variables  and
and 
 | (11.14) |
where  ,
,  . Then we have that
. Then we have that
 | (11.15) |
which, upon inversion, it gives
 | (11.16) |
Therefore it is sufficient to generate a sequence  of uniformly distributed
random numbers and take
of uniformly distributed
random numbers and take
The algorithm shown above gives a sequence of pseudorandom numbers  , which follow the
Gaussian distribution .
The program for
, which follow the
Gaussian distribution .
The program for  is listed below:
is listed below:
!===================================================
!Function to produce random numbers distributed
!according to the gaussian distribution
!g(x) = 1/(sigma*sqrt(2*pi))*exp(-x**2/(2*sigma**2))
!===================================================
real(8) function gaussran()
implicit none
real(8),parameter :: sigma = 1.0D0
real(8) :: r,phi
logical,save :: new = .TRUE.
real(8),save :: x
real(8),parameter :: PI2 = 6.28318530717958648D0
real(8) :: drandom
if(new)then
new = .FALSE.
r = drandom()
phi = PI2*drandom()
r = sigma*sqrt(-2.0D0*log(r))
x = r*cos(phi)
gaussran = r*sin(phi)
else
new = .TRUE.
gaussran = x
endif
end function gaussran
The result is shown in figure 11.7. Notice the SAVE attribute for the variables
new and x. This means that their values are saved between calls of drandom. We
do this because each time we calculate according to (11.17) , we generate two
random numbers, whereas the function returns only one. The function needs to
know whether it is necessary to generate a new pair  (this is what the
“flag” new marks) and, if not, to return the previously generated number, saved in
the variable x. The analysis of the results is left as an exercise to the
reader.
(this is what the
“flag” new marks) and, if not, to return the previously generated number, saved in
the variable x. The analysis of the results is left as an exercise to the
reader.
11.2 Using Pseudorandom Number Generators
The function drandom() is good enough for the problems studied in this
book. However, in many demanding and high accuracy calculations, it is
necessary to use higher quality random numbers and/or have the need of
much longer periods. In this section we will discuss how to use two high
quality, efficient and portable generators which are popular among many
researchers.
The first one is an intrinsic procedure in the Fortran language, the subroutine
RANDOM_NUMBER. The algorithm implemented is not universal and depends on the Fortran
environment .
For the gfortran compiler RANDOM_NUMBER uses the “multiply-with-carry”
algorithm of George Marsaglia in combination with a modulo and shift-register
generator. The period is larger than  . The state of the generator is
determined by more than one numbers. In order to use it we should learn
. The state of the generator is
determined by more than one numbers. In order to use it we should learn
- how to start from a new state
- how to save the current state
- how to restart from a previously saved state
- and, of course, how to obtain the random numbers.
Saving the current state of the generator is very important when we execute a job
that is split in several parts (checkpointing). This is done very often on
computer systems that set time limits for jobs or when our jobs are so long
(more than 8-10 hours) that it will be painful to loose the resources (time
and money) spent for the calculation in case of a computer crash. If we
want to restart the job from exactly the same state as it was before we
stopped, we also need to restart the random number generator from the same
state.
Starting from a new, fresh state is called seeding. The seeding of RANDOM_NUMBER
is done by an unspecified number of NSEEDS integers. In order to get this number,
we should call the subroutine RANDOM_SEED(size = NSEEDS) which returns the
number of seeds NSEEDS when its argument is size = NSEEDS. Then we
have to define the integer values of the array seeds(NSEEDS) and call
again the routine RANDOM_SEED(PUT = seeds) with the argument PUT =
seeds, which will seed the generator from the seeds in seeds. In the code
listed below we show how to seed the generator by using only one integer
seed:
integer :: NSEEDS
integer,allocatable :: seeds(:)
integer :: seed
!---------------------------------------
seed = 47279823
call RANDOM_SEED(size = NSEEDS)
ALLOCATE(seeds(NSEEDS))
seeds = seed + 37 * (/ (i - 1, i = 1, NSEEDS) /)
call RANDOM_SEED(PUT = seeds)
The last line
uses the values stored in the array seeds(1) ... seeds(NSEEDS) in
order to initialize RANDOM_NUMBER. It is important to note that, using this
method, the same seed will generate the same sequence of pseudorandom
numbers.
Sometimes we need to initialize the random number generator from as a
random initial state as possible, so that each time that we run our program, a
different sequence of random numbers is generated. For Unix like systems, like the
GNU/Linux system, we can use the two special files /dev/random and
/dev/urandom in order to generate cryptographic-grade random numbers. These
generate random bits from the current state of the computer and it is practically
impossible to predict the obtained sequence of bits. It is preferable to use
/dev/urandom because /dev/random ceases to work when there are no new
random bits in its pool and waits until they are safely generated. The code that
uses
/dev/urandom for seeding is
open(unit=13, file=’/dev/urandom’, access=’stream’, &
form=’unformatted’)
call RANDOM_SEED(size = NSEEDS)
ALLOCATE(seeds(NSEEDS))
read (13) seeds
close(13)
The special file /dev/urandom provides binary, non printable, data so it is
necessary to open it with the unformatted option. For the same reason, the
command read does not have a format instruction but only the unit number. It
reads the number of bits necessary to fill the array seeds. If we need to work in
an environment where the special file /dev/urandom is not available, it is
possible to seed using the current time and the process number ID. The
latter is necessary in case we start several processes in parallel and we
need different seeds. Check the file seed.f90 in order to see how to do
it .
In order to save the current state of the random number generator use the
subroutine RANDOM_SEED(GET = seeds) with argument GET = seeds.
The call stores the necessary information in the array seeds. We can
save the values of the array seeds in order to use them to restart the
random number generator from exactly the same state. The necessary code
is:
integer :: NSEEDS
integer,allocatable :: seeds(:)
!----------------------------------
call RANDOM_SEED(size = NSEEDS)
ALLOCATE(seeds(NSEEDS))
call RANDOM_SEED(GET = seeds)
open(unit=11,file=’state’)
write(11,*)seeds
In order to restart the generator from a saved state, we read the values of the
array seeds and call RANDOM_SEED(PUT = seeds) with argument PUT = seeds.
The following code reads seeds from a file named state:
open(unit=11,file=’state’)
read(11,*)seeds
call RANDOM_SEED(PUT = seeds)
In order to generate random numbers, we can use a scalar variable and generate
them one by one or we can use an array which RANDOM_NUMBER will fill with
random numbers. The first method has a small overhead and in same cases
we will prefer the second one. The code that applies the first method
is
real(8) :: r
!---------------------------------------
do icount = 1,10
call RANDOM_NUMBER(r)
print *,r
enddo
and the code that applies the second is
integer,parameter :: NR=20
real(8),dimension(NR) :: randoms
call RANDOM_NUMBER(randoms)
print *,randoms
The code in the file test_random_number.f90 implements all of the above tasks
and we list it below:
program use_random_number
implicit none
integer :: NSEEDS
integer,allocatable :: seeds(:)
integer :: seed
real(8) :: r
integer,parameter :: NR=20
real(8),dimension(NR) :: randoms
integer(8) :: icount
integer :: i
!---------------------------------------
!start from a new seed:
seed = 47279823
!get number of seeds for generator:
call RANDOM_SEED(size = NSEEDS)
ALLOCATE(seeds(NSEEDS))
!fill in the rest of the seeds:
seeds = seed + 37 * (/ (i - 1, i = 1, NSEEDS) /)
!initialize the generator from the arrays seeds:
call RANDOM_SEED(PUT = seeds)
!---------------------------------------
!generate random numbers one by one:
do icount = 1,10
call random_number(r)
print *,r
enddo
!generate random numbers in an array:
call random_number(randoms)
print ’(1000G28.17)’,randoms
!---------------------------------------
!save state of random_number:
open(unit=11,file=’rannum.seed’)
call RANDOM_SEED(GET = seeds)
write(11,’(5I20)’)seeds
close(11)
!---------------------------------------
!generate some randoms:
call random_number(randoms)
print ’(A,1000G28.17)’,’#FIRST :’,randoms
!---------------------------------------
!read state of random_number:
open(unit=11,file=’rannum.seed’)
read(11,*)seeds
call RANDOM_SEED(PUT = seeds)
!---------------------------------------
!generate same randoms:
call random_number(randoms)
print ’(A,1000G28.17)’,’#SECOND:’,randoms
end program use_random_number
Use the following commands in order to compile and see the results:
> gfortran test_random_number.f90 -o random_number
> ./random_number
A very high quality, portable random number generator was proposed by
Martin Lüscher [47], and a program that implements it is Ranlux. Besides the
high quality random numbers and a period greater than  , a great advantage
of RANLUX is that it will run in any Fortran environment. The code, which can also
be found in the accompanying software, has been written by Fred James and you
can download it in its original form from the links given in the bibliography [47].
The generator uses a subtract-with-borrow algorithm by Marsaglia and Zaman
[49], which has a very large period but fails some of the statistical tests. Based
on the chaotic properties of the algorithm, Lüscher attributed the problems to
short time autocorrelations and proposed a solution in order to eliminate
them.
, a great advantage
of RANLUX is that it will run in any Fortran environment. The code, which can also
be found in the accompanying software, has been written by Fred James and you
can download it in its original form from the links given in the bibliography [47].
The generator uses a subtract-with-borrow algorithm by Marsaglia and Zaman
[49], which has a very large period but fails some of the statistical tests. Based
on the chaotic properties of the algorithm, Lüscher attributed the problems to
short time autocorrelations and proposed a solution in order to eliminate
them.
In order to start RANLUX using a single seed, use the subroutine RLUXGO. The
necessary code is:
integer :: seed,ranlux_level
!---------------------------------------
seed = 58266273
ranlux_level = 2
call RLUXGO(ranlux_level,seed,0,0)
The value of the variable ranlux_level determines the quality of random
numbers and it can take the values 1, 2, 3 or 4. Setting ranlux_level=2 is enough
for the needs of this book and ranlux_level=3 is the default value. A larger
value of ranlux_level requires more computational effort (see problem).
In order to save the current state of RANLUX, we need an integer array of size
25. A call to the subroutine RLUXUT saves the necessary information in this array.
We can save this array in order to read it at a later time and start the
sequence of random numbers from the same point. The necessary code
is:
integer,parameter :: NSEEDS = 25
integer,dimension(NSEEDS) :: seeds
!---------------------------------------
open(unit=11,file=’ranlux.seed’)
call RLUXUT(seeds)
write(11,*)seeds
close(11)
In order to start RANLUX from a previously saved state we call the subroutine
RLUXIN as follows:
integer,parameter :: NSEEDS = 25
integer,dimension(NSEEDS) :: seeds
open(unit=11,file=’ranlux.seed’)
read(11,*)seeds
call RLUXIN(seeds)
We can generate random numbers one by one and store them in a scalar
variable
real(8) :: r
!---------------------------------------
call ranlux(r,1)
print *,r
or generate many random numbers with one call and store them in a one
dimensional array
integer,parameter :: NR=20
real(8),dimension(NR) :: randoms
!---------------------------------------
call ranlux(randoms,NR)
print *,randoms
where the parameter NR is set equal to the desired value. The program in the
file test_ranlux.f90 implements all of the above tasks and we list it
below:
program use_ranlux
implicit none
integer,parameter :: NSEEDS = 25
integer,dimension(NSEEDS) :: seeds
integer :: seed,ranlux_level
integer(8) :: icount
real(8) :: r
integer,parameter :: NR=20
real(8),dimension(NR) :: randoms
!---------------------------------------
!start from a new seed:
seed = 58266273
ranlux_level = 2
call RLUXGO(ranlux_level,seed,0,0)
!---------------------------------------
!generate random numbers one by one:
do icount = 1,10
call ranlux(r,1)
print *,r
enddo
!generate random numbers in an array:
call ranlux(randoms,NR)
print ’(1000G28.17)’,randoms
!---------------------------------------
!save state of ranlux:
open(unit=11,file=’ranlux.seed’)
call RLUXUT(seeds)
write(11,’(5I20)’)seeds
close(11)
!---------------------------------------
!generate some randoms:
call ranlux(randoms,NR)
print ’(A,1000G28.17)’,’#FIRST :’,randoms
!---------------------------------------
!read state of ranlux:
open(unit=11,file=’ranlux.seed’)
read(11,*)seeds
call RLUXIN(seeds)
!---------------------------------------
!generate same randoms!
call ranlux(randoms,NR)
print ’(A,1000G28.17)’,’#SECOND:’,randoms
end program use_ranlux
Compile the file together with the file ranlux.F, which contains the RANLUX code,
and run it with the commands
> gfortran test_ranlux.f90 ranlux.F -o ranlux
> ./ranlux
11.3 Random Walks
Consider a particle which is located at one of the sites of a two dimensional square
lattice. After equilibrating at this position, it can jump randomly to one of its
nearest neighbor positions. There, it might need some time to equilibrate again
before jumping to a new position. During this time, the momentum that it had at
its arrival is lost, therefore the next jump is made without “memory”
of the previous position where it came from. This process is repeated
continuously. We are not interested in the mechanism that causes the
jumping ,
and we seek a simple phenomenological description of the process.
Assume that the particle jumps in each direction with equal probability and
that each jump occurs after the same time  . The minimum distance between
the lattice sites is
. The minimum distance between
the lattice sites is  (lattice constant). The vector that describes the change of
the position of the particle during the
(lattice constant). The vector that describes the change of
the position of the particle during the  -th jump is a random variable
-th jump is a random variable  and it
always has the same magnitude
and it
always has the same magnitude  . This means that, given the
position
. This means that, given the
position  of the particle at time
of the particle at time  , its position
, its position  at time
at time
 is
is
 | (11.21) |
where
 | (11.22) |
The vectors  and
and  are uncorrelated for
are uncorrelated for  and we have that
and we have that
 | (11.23) |
The possible values of  are equally probable, therefore we obtain
are equally probable, therefore we obtain
 | (11.24) |
This is because the positive and negative terms in the sum performed in the
calculation of  occur with the same frequency and they cancel each other.
Therefore
occur with the same frequency and they cancel each other.
Therefore  for
for  . Since the magnitude of the vectors
. Since the magnitude of the vectors  is
constant, we obtain
is
constant, we obtain
 | (11.25) |
The probability for a path  of length
of length  to occur
is
to occur
is
 | (11.26) |
where  is the number of nearest neighbors of a lattice site. This
probability depends on the length of the path and not on its geometry.
This can be easily seen using the obvious relation
is the number of nearest neighbors of a lattice site. This
probability depends on the length of the path and not on its geometry.
This can be easily seen using the obvious relation  ,
since there are exactly
,
since there are exactly  equally probable cases. The partition function
is
equally probable cases. The partition function
is
 | (11.27) |
and it counts the number of different paths of length  .
.
After time  the particle is displaced from its original position
by
the particle is displaced from its original position
by
 | (11.28) |
The average value of the displacement vanishes
 | (11.29) |
The expectation value of the displacement squared is non zero
 | (11.30) |
The conclusion is that the random walker has been displaced from its original
position rather slowly
 | (11.31) |
For a particle with a non zero average velocity we expect that  .
.
Equation (11.31) defines the critical exponent 
 | (11.32) |
where  means asymptotic behavior in the limit
means asymptotic behavior in the limit  . For a classical
walker
. For a classical
walker  , whereas for the random walker
, whereas for the random walker  .
.
The Random Walker (RW) model has several variations, like the Non Reversal
Random Walker (NRRW) and the Self Avoiding Walk (SAW) . The NRRW model
is defined by excluding the vector pointing to the previous position of the
walker and by selecting the remaining vectors  with equal probability.
The SAW is a NRRW with the additional requirement that, when the
walker ends in a previously visited position, the ... walking ends! Some
models studied in the literature include, besides the infinite repulsive force,
an attractive contribution to the total energy for every pair of points of
the path that are nearest neighbors. In this case, each path is weighted
with the corresponding Boltzmann weight according to equation (12.4)
.
with equal probability.
The SAW is a NRRW with the additional requirement that, when the
walker ends in a previously visited position, the ... walking ends! Some
models studied in the literature include, besides the infinite repulsive force,
an attractive contribution to the total energy for every pair of points of
the path that are nearest neighbors. In this case, each path is weighted
with the corresponding Boltzmann weight according to equation (12.4)
.
For the NRRW, equation (11.32) is similar to that of the RW, i.e.  .
Even though the paths differ microscopically, their long distance properties are
the same. They are examples of models belonging to the same universality class
according to the discussion in section 13.1.
.
Even though the paths differ microscopically, their long distance properties are
the same. They are examples of models belonging to the same universality class
according to the discussion in section 13.1.
This is not the case for the SAW. For this system we have that [50]
 | (11.33) |
therefore the typical paths in this model are longer than those of the RW. If we
introduce a nearest neighbor attraction according to the previous discussion, then
there is a critical temperature  such that for
such that for  we have similar behavior
given by equation (11.33) , whereas for
we have similar behavior
given by equation (11.33) , whereas for  the attractive interaction
dominates, the paths collapse and we obtain
the attractive interaction
dominates, the paths collapse and we obtain  . For
. For  we
have that
we
have that  . For more information we refer the reader to the book of Binder
and Heermann [7].
. For more information we refer the reader to the book of Binder
and Heermann [7].
In order to write a program that simulates the RW we apply the following
algorithm:
- Set the number of the random walks to be generated
- Set the number of steps of each walk
- Set the initial position of the walk
- At each step on the walk, pick a random direction with equal probability
- After the walk is completed, measure
 ,
,  , etc
, etc
- After all walks have been generated, compute the expectation values of
the measured quantities and the statistical error of their measurement.
All we need to explain is how to program the choice of “random direction”.
The program is in the file rw.f90
program random_walker
implicit none
integer,parameter :: Nwalk = 1000
integer,parameter :: Nstep = 100000
integer :: iwalk,istep,ir
real(8) :: x,y
real(8) :: drandom
integer :: seed
common /randoms/ seed
seed = 374676287
open(unit=20,file=’dataR’)
do iwalk = 1,Nwalk
x = 0.0D0 ; y = 0.0D0
open(unit=21,file=’data’)
do istep=1,Nstep
ir = INT(drandom()*4)
select case(ir)
case(0)
x = x + 1.0D0
case(1)
x = x - 1.0D0
case(2)
y = y + 1.0D0
case(3)
y = y - 1.0D0
end select
write(21,*) x,y
enddo !do istep=1,Nstep
close(21)
call sleep(2)
write(20,*) x*x+y*y
call flush(20)
enddo !do iwalk = 1,Nwalk
end program random_walker
The length of the paths is Nstep and the number of the generated paths
is Nwalk. Their values are hard coded and a run using different values
requires recompilation. The results are written to the files dataR and
data. The square of the final displacement of the walker  is written to
dataR and the coordinates
is written to
dataR and the coordinates  of the points visited by the walker
in each path is written to data. In order to make the contents of the
files available immediately, we empty the I/O buffers by a call to the
subroutine flush(unit). The file data is truncated at the beginning
of each path, therefore it contains the coordinates of the current path
only.
of the points visited by the walker
in each path is written to data. In order to make the contents of the
files available immediately, we empty the I/O buffers by a call to the
subroutine flush(unit). The file data is truncated at the beginning
of each path, therefore it contains the coordinates of the current path
only.
Each path is made of Nstep steps. The random vector  is chosen and it
is added in the current position
is chosen and it
is added in the current position  . The choice on
. The choice on  is made in
the line
is made in
the line
ir = INT(drandom()*4)
where the variable ir  because the function INT returns the integer
part of a real. The values of ir correspond to the four possible directions
of
because the function INT returns the integer
part of a real. The values of ir correspond to the four possible directions
of  . We use the construct select case(ir) in order to move in the
direction chosen by ir. Depending on its value, the control of the program is
transferred to the command that moves the walker to the corresponding
direction.
. We use the construct select case(ir) in order to move in the
direction chosen by ir. Depending on its value, the control of the program is
transferred to the command that moves the walker to the corresponding
direction.
Compiling and running the program can be done with the commands
> gfortran rw.f90 drandom.f90 -o rw
> ./rw
Because of the command call sleep(2), the program temporarily halts
execution for 2 seconds at the end of each generated path (you should remove this
line at the production stage). This allows us to monitor the generated
paths graphically. During the execution of the program, use gnuplot
in order to plot the random walk which is currently stored in the file
data:
gnuplot> plot "data" with lines
Repeat for as many times as you wish to see new random walks. The automation
of this process is taken care in the script eternal-rw:
> ./rw &
> ./eternal-rw &
> killall rw eternal-rw gnuplot
The last command ends the execution of all programs.
Some typical paths are shown in figure 11.8. Figure 11.9 shows the results for
the expectation value  for
for  which confirm equation
(11.30)
which confirm equation
(11.30)  .
.
You can reproduce this figure as follows:
- Set the values of Nwalk and Nstep in the file rw.f90. Delete the
commands call sleep(2) and write(21,*) x,y and compile the
code.
- Run the program and analyze the data in the file dataR:
> ./rw
> awk ’{av += $1}END{print av/NR}’ dataR
Write the results in a file r2.dat in two columns with the length of the
paths  in the first column and with
in the first column and with  in the second. The
command
{av+=$1} in the awk program adds the first column of each line of
the file dataR to the variable av. After reading the whole file, the
command END{print av/NR}, prints the variable av divided by the
number of lines in the file (NR = “Number of Records”). This is a
simple way for computing the mean of the first column of the file
dataR.
in the second. The
command
{av+=$1} in the awk program adds the first column of each line of
the file dataR to the variable av. After reading the whole file, the
command END{print av/NR}, prints the variable av divided by the
number of lines in the file (NR = “Number of Records”). This is a
simple way for computing the mean of the first column of the file
dataR.
- Use a linear squares method in order to find the optimal line
 going through the points (
going through the points ( ,
, ). You can also use the fit
command in gnuplot as follows:
). You can also use the fit
command in gnuplot as follows:
gnuplot> fit a*x+b "r2.dat" u (log($1)):(log($2)) via a,b
- Construct the plot with the command:
gnuplot> plot a*x+b,"r2.dat" u (log($1)):(log($2)) w e
The obtained results are meaningless without their statistical errors. Since each
measurement is statistically independent, the true expectation value is
approached in the limit of infinite measurements with a speed proportional to
 , where
, where  is the number of measurements. For the same
reason ,
the statistical error is given by equation (11.3) , e.g.
is the number of measurements. For the same
reason ,
the statistical error is given by equation (11.3) , e.g.
 | (11.34) |
We can add the calculation of the error in the program in rw.f90 or we can leave
this task to external utilities. For example we can use the awk script, which is
written in the file average:
#!/usr/bin/awk -f
{
av += $1; # the sum of data
er += $1*$1; # the sum of squares of data
}
END{
av /= NR; # NR = "Number of Records" = number of lines
er /= NR;
# formula for error of uncorrelated measurements
er = sqrt( (er - av*av)/(NR-1) );
print av, "+/-", er;
}
The contents of this file is an example of a script interpreted by the awk program.
The operating system knows which program to use for the interpretation by
reading the first line #!/bin/awk -f where the first two characters of the program
should be exactly #!. For the commands to be interpreted and executed, one has
to make the script executable using the command chmod a+x average. Then the
command
> ./average dataR
executes the script using the awk interpreter. We remind to the
reader that the commands between curly brackets { ... } are
executed by awk for every line of the file dataR. The commands between
END{ ... } are executed after the last line of the file has been
read .
Therefore the lines
av += $1; # the sum of data
er += $1*$1; # the sum of squares of data
add the first column of the file dataR and its square to the variables av and er
respectively. The commands
av /= NR; # NR = "Number of Records" = number of lines
er /= NR;
are executed after the whole file dataR has been read and divide the variables av
and er with the predefined variable NR which counts the total number of lines
read so far. The last lines of the script compute the error according to equation
(11.34) and print the final result. The shell script in the file rw1-anal.csh codes
all of the above commands in a script. Read the comments in the file for usage
instructions.
11.4 Problems
- Reproduce the results shown in figure 11.6 and confirm the validity of
equation (11.5) .
- Generate a sequence of pseudorandom numbers which follow a Gaussian
distribution with standard deviation
 . Construct the plot
of relative frequencies together with the plot of the probability density
function.
. Construct the plot
of relative frequencies together with the plot of the probability density
function.
- Generate a sequence of pseudorandom numbers which follow the
Cauchy distribution with
 . Construct the plot of relative
frequencies together with the plot of the probability density function.
. Construct the plot of relative
frequencies together with the plot of the probability density function.
- Write a program that calculates the period of the function drandom().
Check whether the numbers 0 and 1 belong to the sequence.
- Compute the CPU time cost of the random number generation as follows: If
you have an executable file, e.g. random, run the /usr/bin/time command
with ./random as its argument:
> /usr/bin/time ./random
Upon exit of the command, the program /usr/bin/time prints the total
CPU time in seconds to the stderr. Compute the time needed to generate
 random numbers using the function drandom() and the subroutines
random_number and ranlux. For RANLUX, measure the CPU time for each
value of ranlux_level from 1 to 4. How does this time depend on
whether the random numbers are generated one by one or in groups of
1000 by calls to random_number and ranlux having as an argument
an array of size 1000? How does the time change if the random
numbers are generated in groups of 10000 instead? (Hint: see the file
performance_ran.f90)
random numbers using the function drandom() and the subroutines
random_number and ranlux. For RANLUX, measure the CPU time for each
value of ranlux_level from 1 to 4. How does this time depend on
whether the random numbers are generated one by one or in groups of
1000 by calls to random_number and ranlux having as an argument
an array of size 1000? How does the time change if the random
numbers are generated in groups of 10000 instead? (Hint: see the file
performance_ran.f90)
- For each of the random number generators drandom(), random_number and
ranlux, generate 10 random numbers. Then save the state of the
generator in a file. Then generate 10 more random numbers. Read from
the file the saved state of the generator and generate 10 random
numbers. Check that the last two sequences of random numbers are
identical.
- Make the appropriate changes in the file seed.f90 so that it can be used for
seeding RANLUX. Do it in two different ways: (a) by generating one seed and
use RLUXGO for the initialization. (b) By generating 25 seeds and use RLUXIN
for the initialization.
- Show that if the expectation values of the vectors
 then
then
 and we obtain a linear relation between displacement–length of
path. The quantity
and we obtain a linear relation between displacement–length of
path. The quantity  is the expectation value of the speed of the particle.
Compute
is the expectation value of the speed of the particle.
Compute  for large values of
for large values of  .
.
- Confirm the relations computed in the previous problem numerically. In
your program, set the first line in (11.22) equal to
 and the rest equal
to
and the rest equal
to  . Compute the expectation values
. Compute the expectation values  and
and  and use them
to calculate the average speed of the particle. Check the validity of the
relations
and use them
to calculate the average speed of the particle. Check the validity of the
relations  and
and 
 . What is the
relation between
. What is the
relation between  ,
,  and
and  ?
?
- Make the appropriate changes in the file rw.f90 so that the user can enter
the values Nwalk and Nstep interactively using the command line
arguments. For example, if she wants to generate 100 random walks with
 , she should run the command ./rw 100 2000. You will need to
use the Fortran intrinsic functions GETARG and IARGC. (Hint: Look in the file
rw1.f90)
, she should run the command ./rw 100 2000. You will need to
use the Fortran intrinsic functions GETARG and IARGC. (Hint: Look in the file
rw1.f90)
- We know that for the RW we have that
 . Calculate
. Calculate  and
and  numerically for
numerically for  . Are they really equal to zero? Why? How
does this depend on the number of measurements?
. Are they really equal to zero? Why? How
does this depend on the number of measurements?
- Compute the expectation value of the number of returns of the RW to his
initial position as a function of
 . What happens as
. What happens as  ?
Why?
?
Why?
- Reproduce figure 11.9 for the RW.
- Write a program that implements the NRRW and reproduce the results in
figure 11.9 for the NRRW.
- In the program rw.f90 the RW’s position is determined by two REAL(8)
variables x,y. The next position is calculated by the statements
x=x+1.0D0, y=y+1.0D0. What are the limitations on the size of random
walks that can be studied with this choice? What happens if one
uses REAL variables x,y instead? Take into account the fact that
 .
.
- Repeat the previous problem by using INTEGER(8) variables x,y. The next
position is calculated by the statements x=x+1, y=y+1. Discuss the pros and
the cons of each choice.
- Repeat the previous problems by using INTEGER(4) variables x,y. Discuss
the pros and the cons of each choice by considering also the running time of
the program. Use the command /usr/bin/time.
- Write a straightforward code that implements the SAW. How big
 can
you simulate? Check whether the CPU time for computing a given number
of random walks increases exponentially with
can
you simulate? Check whether the CPU time for computing a given number
of random walks increases exponentially with  . Search the internet
for the most efficient algorithm that simulates the SAW for large
. Search the internet
for the most efficient algorithm that simulates the SAW for large
 .
.
Chapter 12
Monte Carlo Simulations
In this chapter we review the basic principles of Monte Carlo simulations in
statistical mechanics. In the introduction, we review some of the fundamental
concepts of statistical physics. The reader should have a basic understanding of
concepts like the canonical ensemble, the partition function, the entropy,
the density of states and the quantitative description of fluctuations of
thermodynamic quantities. For a more in depth discussion of these concepts, see
[4, 43, 51, 52, 53, 54].
For most of the interesting systems, the partition function cannot be
calculated analytically, and in such a case we may resort to a numerical
computation. This is what is done most effectively using Monte Carlo simulations,
which consist of collecting a statistical sample of states of the system
with an appropriately chosen probability distribution. It is remarkable
that, by collecting a sample which is a tiny fraction of the total number
of states, we can perform an accurate calculation of its thermodynamic
quantities .
But this is no surprise: it happens in our labs all the
time !
12.1 Statistical Physics
Statistical physics describes systems with a very large number of degrees of
freedom  . For simple macroscopic systems
. For simple macroscopic systems  –
–  . For such
systems, it is practically impossible to solve the microscopic equations that
govern their dynamics. Even if we could, the solution would have had much
more information than we need (and capable of analyzing!). It is enough,
however, to know a small number of bulk properties of the system in
order to have a useful description of it. E.g. it is enough to know the
internal energy and magnetization of a magnet or the energy and density of
a fluid instead of the detailed knowledge of the position, momentum,
energy and angular momentum of each particle they are made of. These
quantities provide a thermodynamic description of a system. Statistical
physics makes an attempt to derive these quantities from the microscopic
degrees of freedom and their dynamics given by the Hamiltonian of the
system.
. For such
systems, it is practically impossible to solve the microscopic equations that
govern their dynamics. Even if we could, the solution would have had much
more information than we need (and capable of analyzing!). It is enough,
however, to know a small number of bulk properties of the system in
order to have a useful description of it. E.g. it is enough to know the
internal energy and magnetization of a magnet or the energy and density of
a fluid instead of the detailed knowledge of the position, momentum,
energy and angular momentum of each particle they are made of. These
quantities provide a thermodynamic description of a system. Statistical
physics makes an attempt to derive these quantities from the microscopic
degrees of freedom and their dynamics given by the Hamiltonian of the
system.
Consider a system which can be in a set of discrete states which belong to a countable
set  . The energy spectrum of those states is assumed to consist of discrete
values
. The energy spectrum of those states is assumed to consist of discrete
values
 . This system is in contact and interacts with a large
heat reservoir which has temperature
. This system is in contact and interacts with a large
heat reservoir which has temperature  . The contact with the
reservoir results in random transitions which change the energy of the
system .
The system is described by the weights
. The contact with the
reservoir results in random transitions which change the energy of the
system .
The system is described by the weights  which give the probability to find
the system in a state
which give the probability to find
the system in a state  at time
at time  . These weights are the connection between the
microscopic and statistical description of the system. When this system is in
thermal equilibrium with the reservoir, its statistical properties are described by
the, so called, canonical ensemble.
. These weights are the connection between the
microscopic and statistical description of the system. When this system is in
thermal equilibrium with the reservoir, its statistical properties are described by
the, so called, canonical ensemble.
Let  be the transition rates from the state
be the transition rates from the state  , i.e.
, i.e.
 | (12.1) |
which depend on the interaction between the system and the thermal reservoir.
The master equation for the weights  is
is
The first of the above equations tells us that the change in  is equal to
the rate that the system comes into the state
is equal to
the rate that the system comes into the state  from any other state
from any other state
 , minus the rate of leaving the state
, minus the rate of leaving the state  . The second equation is a
result of the probability interpretation of the weights
. The second equation is a
result of the probability interpretation of the weights  and states
that the probability of finding the system in any state is equal to 1 at all
times.
and states
that the probability of finding the system in any state is equal to 1 at all
times.
The transition rates  are assumed to be time independent
and then the above system of equations for
are assumed to be time independent
and then the above system of equations for  is linear with real
parameters. This, together with the constraint
is linear with real
parameters. This, together with the constraint  , implies
that ,
in the large time limit,
, implies
that ,
in the large time limit,  and the system reaches equilibrium. Then, the
and the system reaches equilibrium. Then, the
 converge to finite numbers
converge to finite numbers  . These are the equilibrium occupation
probabilities
. These are the equilibrium occupation
probabilities
For a system in thermodynamic equilibrium with a reservoir in temperature  ,
with
,
with  , the probabilities
, the probabilities  follow the Boltzmann distribution (Gibbs
1902)
follow the Boltzmann distribution (Gibbs
1902)
 | (12.4) |
and define the, so called, canonical ensemble. The parameter  will be frequently
referred to as simply “the temperature” of the system, although, strictly speaking,
it is the inverse of it. Its appearance in the exponential in equation (12.4) ,
defines a characteristic energy scale of the system. The Boltzmann constant
will be frequently
referred to as simply “the temperature” of the system, although, strictly speaking,
it is the inverse of it. Its appearance in the exponential in equation (12.4) ,
defines a characteristic energy scale of the system. The Boltzmann constant
 is simply a conversion constant between units of
energy .
is simply a conversion constant between units of
energy .
The normalization  in equation (12.4) is the so called partition function of
the system. The condition
in equation (12.4) is the so called partition function of
the system. The condition  implies
implies
 | (12.5) |
The measurement of a physical quantity, or observable, of a thermodynamic
system has a stochastic character. For systems with very large number of degrees
of freedom  , one is interested only in the average value of such a quantity. This
is because the probability of measuring the quantity to take a value significantly
different from its average is ridiculously small. The average, or expectation value,
, one is interested only in the average value of such a quantity. This
is because the probability of measuring the quantity to take a value significantly
different from its average is ridiculously small. The average, or expectation value,
 of a physical observable
of a physical observable  whose value in a state
whose value in a state  is
is  is equal
to
is equal
to
 | (12.6) |
As we will see later, the standard deviation  for a typical thermodynamic
system is such that
for a typical thermodynamic
system is such that
 | (12.7) |
which is quite small for macroscopic
systems .
In such cases, the fluctuations of the values of  from its expectation value
from its expectation value
 can be neglected. The limit
can be neglected. The limit  is the so called thermodynamic limit,
and it is in this limit in which we are studying systems in statistical mechanics.
Most systems in the lab are practically in this limit, but in the systems simulated
on a computer we may be far from it. The state of the art is to invent methods
which can be used to extrapolate the results from the study of the finite system to
the thermodynamic limit efficiently.
is the so called thermodynamic limit,
and it is in this limit in which we are studying systems in statistical mechanics.
Most systems in the lab are practically in this limit, but in the systems simulated
on a computer we may be far from it. The state of the art is to invent methods
which can be used to extrapolate the results from the study of the finite system to
the thermodynamic limit efficiently.
Because of (12.5) , the partition function encodes all the statistical
information about the system. It is not just a simple function of one or more
variables, but it counts all the states of the system with the correct weight. Its
knowledge is equivalent to being able to compute any thermodynamic
quantity like, for example, the expectation value of the energy  of the
system :
of the
system :
Similarly, one can calculate the specific heat from
 | (12.9) |
12.2 Entropy
The entropy  of a thermodynamic system is defined by
of a thermodynamic system is defined by
 | (12.10) |
where  is the free energy if the system. We will attempt to provide microscopic
definitions that are consistent with the above equations.
is the free energy if the system. We will attempt to provide microscopic
definitions that are consistent with the above equations.
We define the free energy from the relation
or equivalently Note that for  the free energy becomes the ground state
energy .
Indeed, as
the free energy becomes the ground state
energy .
Indeed, as  only the lowest energy term in equation (12.11) survives.
For this reason, equation (12.10) gives
only the lowest energy term in equation (12.11) survives.
For this reason, equation (12.10) gives  , which is the third law of
thermodynamics.
, which is the third law of
thermodynamics.
The definition (12.11) is consistent with (12.10) since
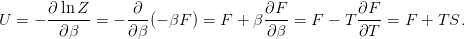 | (12.13) |
The relation of the entropy  to the microscopic degrees of freedom can be
derived from equations (12.11) and (12.10) :
to the microscopic degrees of freedom can be
derived from equations (12.11) and (12.10) :
 | (12.14) |
But
 | (12.15) |
therefore
Finally
 | (12.17) |
Let’s analyze the above relation in some special cases. Consider a
system
where all possible states have the same energy. For such a system, using equation
(12.17) , we obtain that
 | (12.18) |
Therefore, the entropy simply counts the number of states of the system. This is
also the case in the microcanonical ensemble. Indeed, equation (12.18) is also
valid for the distribution
 | (12.19) |
which can be considered to be equivalent to the microcanonical ensemble
since it enforces  Equation (12.19) can viewed as an
approximation to a distribution sharply peaked at
Equation (12.19) can viewed as an
approximation to a distribution sharply peaked at  . In such a case,
. In such a case,  counts,
more or less, the number of states of the system with energy close to
counts,
more or less, the number of states of the system with energy close to
 .
.
In general, the function
 is defined to be equal to the number of states with energy equal to
is defined to be equal to the number of states with energy equal to  .
Then the probability
.
Then the probability  to measure energy
to measure energy  in the canonical ensemble
is
in the canonical ensemble
is
 | (12.20) |
Since  , we obtain
, we obtain
 | (12.21) |
For a generic system we have that
 | (12.22) |
where  is the number of degrees of freedom of the system and
is the number of degrees of freedom of the system and  is a constant.
is a constant.
The qualitative behavior of the distribution (12.21) is shown in figure 12.1.
For such a system the most probable values of the energy are sharply peaked
around a value  and the deviation
and the deviation  is a measure of the energy
fluctuations. The ratio
is a measure of the energy
fluctuations. The ratio  drops with
drops with  as
as  . Indeed, the
function
. Indeed, the
function
 | (12.23) |
has a maximum when
 | (12.24) |
or
 | (12.25) |
As the temperature increases ( decreases),
decreases),  shifts to larger values.
shifts to larger values.  is
proportional to the system size. By Taylor expanding around
is
proportional to the system size. By Taylor expanding around  we obtain
we obtain
where we used equation (12.24) and computed  . Therefore
. Therefore
 | (12.27) |
which is a Gaussian distribution with standard deviation
 | (12.28) |
Therefore we confirm the relation (12.7)
 | (12.29) |
In the analysis above we assumed analyticity (Taylor expansion, equation (12.26)
), which is not valid at a critical point of a phase transition in the thermodynamic
limit.
Another important case where the above analysis becomes slightly more
complicated is when the distribution  has more than one equally probable
maxima
separated by a large probability barrier as shown in figure 12.2 like when the
system undergoes a first order phase transition. Such a transition occurs when ice
turns into water or when a ferromagnet looses its permanent magnetization due to
temperature increase past its Curie point. In such a case the two states, ice –
water / ferromagnet – paramagnet, are equally probable and coexist. This is
qualitatively depicted in figure 12.2.
has more than one equally probable
maxima
separated by a large probability barrier as shown in figure 12.2 like when the
system undergoes a first order phase transition. Such a transition occurs when ice
turns into water or when a ferromagnet looses its permanent magnetization due to
temperature increase past its Curie point. In such a case the two states, ice –
water / ferromagnet – paramagnet, are equally probable and coexist. This is
qualitatively depicted in figure 12.2.
12.3 Fluctuations
The stochastic behavior of every observable  is given by a distribution function
is given by a distribution function
 which can be derived from the Boltzmann distribution (12.4) . Such a
distribution is completely determined by its expectation value
which can be derived from the Boltzmann distribution (12.4) . Such a
distribution is completely determined by its expectation value  and
all its higher order moments, i.e. the expectation values
and
all its higher order moments, i.e. the expectation values  ,
,
 . The most commonly studied moment is the second moment
(
. The most commonly studied moment is the second moment
( )
)
 | (12.30) |
For a distribution with a single maximum,  is a measure of the fluctuations
of
is a measure of the fluctuations
of  away from its expectation value
away from its expectation value  . When
. When  we obtain
we obtain
 | (12.31) |
and using the relations
 | (12.32) |
and
 | (12.33) |
we obtain that
 | (12.34) |
which, according to (12.9) , is the specific heat
 | (12.35) |
This way we relate the specific heat of a system (a thermodynamic quantity) with
the microscopic fluctuations of the energy.
This is true for every physical quantity which is linearly coupled to an external
field (in the case of  , this role is played by
, this role is played by  ). For a magnetic system in a
constant magnetic field
). For a magnetic system in a
constant magnetic field  , such a quantity is the magnetization
, such a quantity is the magnetization  . If
. If  is
the magnetization of the system in the sate
is
the magnetization of the system in the sate  and we assume that its direction is
parallel to the direction of the magnetic field
and we assume that its direction is
parallel to the direction of the magnetic field  , then the Hamiltonian of the
system is
, then the Hamiltonian of the
system is
 | (12.36) |
and the partition function is
 | (12.37) |
“Linear coupling” signifies the presence of the linear term  in the
Hamiltonian. The quantities
in the
Hamiltonian. The quantities  and
and  are called conjugate to each other.
Other well known conjugate quantities are the pressure/volume (
are called conjugate to each other.
Other well known conjugate quantities are the pressure/volume ( /
/ ) in a gas
or the chemical potential/number of particles (
) in a gas
or the chemical potential/number of particles ( /
/ ) in the grand canonical
ensemble.
) in the grand canonical
ensemble.
Because of this linear coupling we obtain
 | (12.38) |
which is analogous to (12.8) . The equation corresponding to (12.34) is obtained
from (12.30) for 
 | (12.39) |
From (12.37) we obtain
 | (12.40) |
therefore
 | (12.41) |
The magnetic susceptibility  is defined by the equation
is defined by the equation
 | (12.42) |
where we see its relation to the fluctuations of the magnetization. This analysis
can be repeated in a similar way for every pair of conjugate quantities.
12.4 Correlation Functions
The correlation functions can be obtained is a similar manner when we consider
external fields which are space dependent. For simplicity, consider a system
defined on a discrete lattice, whose sites are mapped to natural numbers
 . Then the magnetic field
. Then the magnetic field  is a function of the position
is a function of the position  and
interacts with the spin
and
interacts with the spin  so that
so that
 | (12.43) |
Then the magnetization per site
 at position
at position  is
is
 | (12.44) |
The connected two point correlation function is defined by
 | (12.45) |
When the values of  and
and  are strongly correlated, i.e. they “vary together”
in the random samples that we take, the function (12.45) takes on large positive
values. When the values of
are strongly correlated, i.e. they “vary together”
in the random samples that we take, the function (12.45) takes on large positive
values. When the values of  and
and  are not at all correlated with
each other, the terms
are not at all correlated with
each other, the terms  in the sum over
in the sum over  in the
expectation value
in the
expectation value  cancel each other and
cancel each other and  is
zero .
is
zero .
The function  takes its maximum value
takes its maximum value  for
for  .
Then it falls off quite fast. For a generic system
.
Then it falls off quite fast. For a generic system
 | (12.46) |
where  is the distance between the points
is the distance between the points  and
and  . The correlation length
. The correlation length
 , is a characteristic length scale of the system which is a measure of the
distance where there is a measurable correlation between the magnetic moments
of two lattice sites. It depends on the parameters that define the system
, is a characteristic length scale of the system which is a measure of the
distance where there is a measurable correlation between the magnetic moments
of two lattice sites. It depends on the parameters that define the system
 . It is important to stress that it is a length scale that arises
dynamically. In contrast, length scales like the size of the system
. It is important to stress that it is a length scale that arises
dynamically. In contrast, length scales like the size of the system  or the lattice
constant
or the lattice
constant  are parameters of the system which don’t depend on the dynamics. In
most of the cases,
are parameters of the system which don’t depend on the dynamics. In
most of the cases,  is of the order of a few lattice constants
is of the order of a few lattice constants  and such a
system does not exhibit correlations at macroscopic scales (i.e. of the order of
and such a
system does not exhibit correlations at macroscopic scales (i.e. of the order of
 ).
).
Interesting physics arises when  . This can happen by fine tuning the parameters
on which
. This can happen by fine tuning the parameters
on which  depends on to their critical values. For example, in the neighborhood of a
continuous
phase transition, the exponential falloff in (12.46) vanishes and
depends on to their critical values. For example, in the neighborhood of a
continuous
phase transition, the exponential falloff in (12.46) vanishes and  falls
off like a power (see figure 12.3)
falls
off like a power (see figure 12.3)
 | (12.47) |
where  is the number of dimensions of space and
is the number of dimensions of space and  a critical exponent. As we approach the
critical point ,
correlations extend to distances
a critical exponent. As we approach the
critical point ,
correlations extend to distances  . Then the system is not sensitive to the
short distance details of the lattice and its dynamics are very well approximated
by continuum space dynamics. Then we say that we obtain the continuum limit of
a theory which is microscopically defined on a lattice. Since the microscopic
details become irrelevant, a whole class of theories with different microscopic
definitions
have the same continuum limit. This phenomenon is called universality and plays
a central role in statistical physics and quantum field theories.
. Then the system is not sensitive to the
short distance details of the lattice and its dynamics are very well approximated
by continuum space dynamics. Then we say that we obtain the continuum limit of
a theory which is microscopically defined on a lattice. Since the microscopic
details become irrelevant, a whole class of theories with different microscopic
definitions
have the same continuum limit. This phenomenon is called universality and plays
a central role in statistical physics and quantum field theories.
12.5 Sampling
Our main goal is to calculate the expectation value  ,
,
 | (12.48) |
of a physical quantity, or observable,  of a statistical system in the canonical
ensemble approximately. For this reason we construct a sample of
of a statistical system in the canonical
ensemble approximately. For this reason we construct a sample of  states
states 


 which are distributed according to a chosen
probability distribution
which are distributed according to a chosen
probability distribution  . We define the estimator
. We define the estimator  of
of  to
be
to
be
 | (12.49) |
The above equation is easily understood since, for a large enough sample,
 , and we expect that
, and we expect that
 | (12.50) |
Our goal is to find an appropriate  so that the convergence of (12.50) is as
fast as possible. Consider the following cases:
so that the convergence of (12.50) is as
fast as possible. Consider the following cases:
12.5.1 Simple Sampling
We choose  , and equation (12.49) becomes
, and equation (12.49) becomes
 | (12.51) |
The problem with this choice is the small overlap of the sample with the states
that make the most important contributions to the sum in (12.48) . As we
have already mentioned in the introduction, the size of the sample in a
Monte Carlo simulation is a minuscule fraction of the total number of
states. Therefore, the probability of picking the ones that make important
contributions to the sum in (12.48) is very small. Consider for example the case
 in a generic model. According to equation (12.21) we have
that
in a generic model. According to equation (12.21) we have
that
 | (12.52) |
where  is the probability of measuring energy
is the probability of measuring energy  in the system. A
qualitative plot of
in the system. A
qualitative plot of  is shown in figure 12.1. From (12.25) and (12.28) we
have that
is shown in figure 12.1. From (12.25) and (12.28) we
have that  and
and  , therefore for
, therefore for  and
and  the
qualitative behavior of the respective
the
qualitative behavior of the respective  distributions is shown in figure 12.4.
distributions is shown in figure 12.4.
The distribution of the simple sampling corresponds to the
case  in equation (12.4) , since
in equation (12.4) , since  const. in this
case .
In order to calculate the sum (12.52) with acceptable accuracy for
const. in this
case .
In order to calculate the sum (12.52) with acceptable accuracy for  we
have to obtain a good sample in the region where the product
we
have to obtain a good sample in the region where the product  is
relatively important. The probability of obtaining a state such that
is
relatively important. The probability of obtaining a state such that  is
non negligible is very small when we use the
is
non negligible is very small when we use the  distribution. This can be
seen pictorially in figure 12.4.
distribution. This can be
seen pictorially in figure 12.4.
Even though this method has this serious shortcoming, it could still be useful
in some cases. We have already applied it in the study of random walks. Note
that, by applying equation (12.51) , we can use the same sample for calculating
expectation values for all values of  .
.
12.5.2 Importance Sampling
From the previous discussion it has become clear that, for a large system, a very
small fraction of the space of states makes a significant contribution to the
calculation of  . If we choose a sample with probability
. If we choose a sample with probability
 | (12.53) |
then we expect to sample exactly within this region. Indeed, the estimator, given
by equation (12.49) , is calculated from
 | (12.54) |
Sampling this way is called importance sampling, and it is the method of choice in
most Monte Carlo simulations. The sample depends on the temperature  and
the calculation of the expectation values (12.54) requires a new sample for
each
and
the calculation of the expectation values (12.54) requires a new sample for
each
 . This extra effort, however, is much smaller than the one required in order to
overcome the overlap problem discussed in the previous subsection.
. This extra effort, however, is much smaller than the one required in order to
overcome the overlap problem discussed in the previous subsection.
12.6 Markov Processes
Sampling according to a desired probability distribution  is not possible in a
direct way. For example, if we attempt to construct a sample according to
is not possible in a
direct way. For example, if we attempt to construct a sample according to
 by picking a state
by picking a state  by chance and add it to the sample with
probability
by chance and add it to the sample with
probability  , then we have a very small probability to accept that state in the
sample. Therefore, the difficulty of constructing the sample runs into the same
overlap problem as in the case of simple sampling. For this reason we construct a
Markov chain instead. The members of the sequence of the chain will be our
sample. A Markov process, or a Markov chain, is a stochastic process which, given
the system in a state
, then we have a very small probability to accept that state in the
sample. Therefore, the difficulty of constructing the sample runs into the same
overlap problem as in the case of simple sampling. For this reason we construct a
Markov chain instead. The members of the sequence of the chain will be our
sample. A Markov process, or a Markov chain, is a stochastic process which, given
the system in a state  , puts the system in a new state
, puts the system in a new state  in such a way that it
has the Markov property, i.e. that it is memoryless. This means that a chain of
states
in such a way that it
has the Markov property, i.e. that it is memoryless. This means that a chain of
states
 | (12.55) |
is constructed in such a way that the transition probabilities  from the
state
from the
state  to a new state
to a new state  satisfy the following requirements:
satisfy the following requirements:
- They are independent of “time”
- They depend only on the states
 and
and  and not on the path that the
system has followed on order to get to the sate
and not on the path that the
system has followed on order to get to the sate  (memorylessness)
(memorylessness)
- The relation
 | (12.56) |
holds. Beware, in most of the cases  , i.e. the system has a
nonzero probability to remain in the same state
, i.e. the system has a
nonzero probability to remain in the same state
- For
 the sample
the sample  follows the
follows the  distribution.
distribution.
Then our sample will be  . We may imagine that
this construction happens in “time”
. We may imagine that
this construction happens in “time”  . In a Monte Carlo
simulation we construct a sample from a Markov chain by appropriately
choosing the transition probabilities
. In a Monte Carlo
simulation we construct a sample from a Markov chain by appropriately
choosing the transition probabilities  so that the convergence 4. is
fast.
so that the convergence 4. is
fast.
Choosing the initial state  can become a non trivial task. If it turns out
not to be a typical state of the sample, then it could take a long “time” for the
system to “equilibrate”, i.e. for the Markov process to start sampling
states typical of the simulated temperature. The required time for this to
happen is called the thermalization time which can become a serious part
of our computational effort if we make a wrong choice of
can become a non trivial task. If it turns out
not to be a typical state of the sample, then it could take a long “time” for the
system to “equilibrate”, i.e. for the Markov process to start sampling
states typical of the simulated temperature. The required time for this to
happen is called the thermalization time which can become a serious part
of our computational effort if we make a wrong choice of  and/or
and/or
 .
.
A necessary condition for the sample to converge to the desired distribution is
for the process to be ergodic. This means that for every state  it is possible to
reach any other state
it is possible to
reach any other state  in a finite number of steps. If this criterion is
not satisfied and a significant part of phase space is not sampled, then
sampling will fail. Usually, given a state
in a finite number of steps. If this criterion is
not satisfied and a significant part of phase space is not sampled, then
sampling will fail. Usually, given a state  , the reachable states
, the reachable states  at
the next step (i.e. the states for which
at
the next step (i.e. the states for which  ) are very few.
Therefore the ergodicity of the algorithm considered must be checked
carefully .
) are very few.
Therefore the ergodicity of the algorithm considered must be checked
carefully .
12.7 Detailed Balance Condition
Equation (12.2) tells us that, in order to find the system in equilibrium in the
 distribution, the transition probabilities should be such that
distribution, the transition probabilities should be such that
 | (12.57) |
This means that the rate that the system comes into the state  is equal to the
rate in which it leaves
is equal to the
rate in which it leaves  . From equation (12.56) we obtain
. From equation (12.56) we obtain
 | (12.58) |
This condition is necessary but it is not sufficient (see section 2.2.3 in [4]). A
sufficient, but not necessary, condition is the detailed balance condition. When the
transition probabilities satisfy
 | (12.59) |
then the system will equilibrate to  after sufficiently long thermalization time.
By summing both sides of (12.59) , we obtain the equilibrium condition (12.57) .
For the canonical ensemble (12.4) the condition becomes
after sufficiently long thermalization time.
By summing both sides of (12.59) , we obtain the equilibrium condition (12.57) .
For the canonical ensemble (12.4) the condition becomes
 | (12.60) |
One can show that if the transition probabilities satisfy the above conditions
then the equilibrium distribution of the system will be the Boltzmann
distribution (12.4) . A program implementing a Monte Carlo simulation of a
statistical system in the canonical ensemble consists of the following main
steps:
- Write a program that codes appropriately chosen transition
probabilities
 that satisfy condition (12.60)
that satisfy condition (12.60)
- Choose an initial state

- Let the system evolve until it thermalizes to the Boltzmann distribution
(12.4) (thermalization)
- Collect data for the observables
 and calculate the estimators
and calculate the estimators  from equation (12.54)
from equation (12.54)
- Stop when the desired accuracy in the calculation of
 has been
achieved.
has been
achieved.
Equation (12.60) has many solutions. For a given problem, we are looking for
the most efficient one. Below we list some possible choices:
 | (12.61) |
 | (12.62) |
 | (12.63) |
for appropriately chosen states  and
and
 | (12.64) |
 for any other state
for any other state  . In order for (12.64) to be meaningful,
the constant
. In order for (12.64) to be meaningful,
the constant  has to be chosen so that
has to be chosen so that
 | (12.65) |
Equation (12.65) gives much freedom in the choice of transition probabilities.
In most cases, we split  in two independent parts
in two independent parts
 | (12.66) |
The probability  is the selection probability of the state
is the selection probability of the state  when the
system is in the state
when the
system is in the state  . Therefore the first step in the algorithm is to select a
state
. Therefore the first step in the algorithm is to select a
state  with probability
with probability  .
.
The second step is to accept the change with probability  . If the
answer is no, then the system remains in the state
. If the
answer is no, then the system remains in the state  . This way equation
(12.64) is satisfied. The probabilities
. This way equation
(12.64) is satisfied. The probabilities  are called the acceptance
ratios.
are called the acceptance
ratios.
The art in the field is to device algorithms that give the maximum possible
acceptance ratios for the new states  and that the states
and that the states  are as much as
possible statistically independent from the original state
are as much as
possible statistically independent from the original state  . An ideal situation is
to have
. An ideal situation is
to have  for all
for all  for which
for which  . As we will see in a
following chapter, this is what happens in the case of the Wolff cluster
algorithm.
. As we will see in a
following chapter, this is what happens in the case of the Wolff cluster
algorithm.
12.8 Problems
- Prove equation (12.18) .
- Prove equation (12.19) .
- Prove equation (12.45) .
- Show that equations (12.61) – (12.63) satisfy (12.60) .
Chapter 13
Simulation of the  Ising Model
Ising Model
This chapter is an introduction to the basic Monte Carlo methods used in the
simulations of the Ising model on a two dimensional rectangular lattice,
but also in a wide spectrum of scientific applications. We will introduce
the Metropolis algorithm, which is the most common algorithm used
in Monte Carlo simulations. We will discuss the thermalization of the
system and the effect of correlations between successive spin configurations
generated during the simulation. The autocorrelation function and the
time scale defined by it, the autocorrelation time, are measures of these
autocorrelations and play a central role in the study of the statistical
independence of our measurements. Beating autocorrelations is crucial in Monte
Carlo simulations since they are the main obstacle for studying large
systems, which in turn is essential for taking the thermodynamic limit
without the systematic errors introduced by finite size effects. We will also
introduce methods for the computation of statistical errors that take into
account autocorrelations. The determination of statistical errors is of
central importance in order to assess the quality of a measurement and
predict the amount of resources needed for reaching a specific accuracy
goal.
13.1 The Ising Model
The Ising model (1925) [55] has played an important role in the evolution of
ideas in statistical physics and quantum field theory. In particular, the two
dimensional model is complicated enough in order to possess nontrivial properties
but simple enough in order to be able to obtain an exact analytic solution. The
zero magnetic field model has a 2nd order phase transition for a finite value of the
temperature and we are able to compute critical exponents and study its
continuum limit in detail. This gives us valuable information on the non analytic
properties of a system undergoing a second order phase transition, the appearance
of scaling, the renormalization group and universality. Using the exact
solution
of Onsager (1948) [56] and others, we obtain exact results and compare them
with those obtained via approximate methods, like Monte Carlo simulations,
high and low temperature expansions, mean field theory etc. The result
is also interesting from a physics point of view, since it is the simplest,
phenomenologically interesting, model of a ferromagnetic material. Due to
universality, the model describes also the liquid/vapor phase transition at
the triple point. A well known textbook for a discussion of statistical
mechanical models that can be solved exactly is the book by Baxter [54].
In order to define the model, consider a two dimensional square lattice like the
one shown in figure 13.1. On each site or node of the lattice we have an “atom” or
a “magnet” of spin  . The geometry is determined by the distance of the
nearest neighbors, the lattice constant
. The geometry is determined by the distance of the
nearest neighbors, the lattice constant  , and the number of sites
, and the number of sites  .
Each side consists of
.
Each side consists of  sites so that
sites so that  , where
, where  is
the dimension of space. The topology is determined by the way sites are
connected with each other via links. Special care is given to the sites
located on the sides of the lattice. We usually take periodic boundary
conditions which is equivalent to identifying the opposite sides of the square
by connecting their sites with a link. This is depicted in figure (13.1) .
Periodic boundary conditions endow the plane on which the lattice is defined
with a toroidal topology. The system’s dynamics are determined by the
spin–spin interaction. We take it to be short range and the simplest case
considered here takes into account only nearest neighbor interactions.
is
the dimension of space. The topology is determined by the way sites are
connected with each other via links. Special care is given to the sites
located on the sides of the lattice. We usually take periodic boundary
conditions which is equivalent to identifying the opposite sides of the square
by connecting their sites with a link. This is depicted in figure (13.1) .
Periodic boundary conditions endow the plane on which the lattice is defined
with a toroidal topology. The system’s dynamics are determined by the
spin–spin interaction. We take it to be short range and the simplest case
considered here takes into account only nearest neighbor interactions.
In the Ising model, spins have two possible values, “up” or “down” which we
map
to the numerical values  or
or  . For the ferromagnetic model, each link
is a “bond” whose energy is higher when the spins on each side of the
link are pointing in the same direction and lower when they point in the
opposite
direction. This is depicted in figure 13.1. The system could also be immersed in a
constant magnetic field
. For the ferromagnetic model, each link
is a “bond” whose energy is higher when the spins on each side of the
link are pointing in the same direction and lower when they point in the
opposite
direction. This is depicted in figure 13.1. The system could also be immersed in a
constant magnetic field  whose direction is parallel to the direction of the
spins.
whose direction is parallel to the direction of the
spins.
We are now ready to write the Hamiltonian and the partition function of the
system. Consider a square lattice of  lattice sites (or vertices) labeled by a number
lattice sites (or vertices) labeled by a number
 . The lattice has
. The lattice has  links (or bonds) among nearest neighbors.
These are labeled by
links (or bonds) among nearest neighbors.
These are labeled by 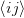 , where
, where  is the pair of vertices on each side of the
link. We identify the sides of the square like in figure 13.1. Then, since two
vertices are connected by one link and four links intersect at one vertex, we have
that
is the pair of vertices on each side of the
link. We identify the sides of the square like in figure 13.1. Then, since two
vertices are connected by one link and four links intersect at one vertex, we have
that
 | (13.1) |
At each vertex we place a spin  . The Hamiltonian of the system is given
by
. The Hamiltonian of the system is given
by
 | (13.2) |
The first term is the spin–spin interaction and for  the system is
ferromagnetic. In this book, we consider only the
the system is
ferromagnetic. In this book, we consider only the  case. A link connecting
same spins has energy
case. A link connecting
same spins has energy  , whereas a link connecting opposite spins
has energy
, whereas a link connecting opposite spins
has energy  . The difference of the energy between the two states
is
. The difference of the energy between the two states
is  and the spin-spin dynamics favor links connecting same spins.
The minimum energy
and the spin-spin dynamics favor links connecting same spins.
The minimum energy  is obtained for the ground state, which is the
unique state in which all
spins point in the direction
of
is obtained for the ground state, which is the
unique state in which all
spins point in the direction
of  . This is equal to
. This is equal to
 | (13.3) |
The partition function is
![∑ ∑ ∑ −βH [{si}] ∑ βJ∑ ⟨ij⟩sisj+βB ∑i si
Z = ... e ≡ e ,
s1= ±1s2=±1 sN= ±1 {si}](main_latex4678x.png) | (13.4) |
where  is a spin configuration of the system. The number
of terms is equal to the number of configurations
is a spin configuration of the system. The number
of terms is equal to the number of configurations  , which is equal to
, which is equal to  , i.e.
it increases exponentially with
, i.e.
it increases exponentially with  . For a humble
. For a humble  lattice we have
lattice we have
 terms.
terms.
The two dimensional Ising model for  has the interesting property that,
for
has the interesting property that,
for  , where
, where
 | (13.5) |
it undergoes a phase transition between an ordered or low temperature phase
where the system is magnetized ( ) and a disordered or high temperature
phase where the magnetization vanishes (
) and a disordered or high temperature
phase where the magnetization vanishes ( ). The magnetization
). The magnetization  distinguishes between the two phases and it is called the order parameter. The
critical temperature
distinguishes between the two phases and it is called the order parameter. The
critical temperature  is the Curie temperature. The phase transition is of second
order, which is a special case of a continuous phase transition. For a continuous
phase transition the order parameter is continuous at
is the Curie temperature. The phase transition is of second
order, which is a special case of a continuous phase transition. For a continuous
phase transition the order parameter is continuous at  , but it is non
analytic .
For a second order phase transition, its derivative is not continuous. This is
qualitatively depicted in figure 13.1.
, but it is non
analytic .
For a second order phase transition, its derivative is not continuous. This is
qualitatively depicted in figure 13.1.
For  the correlation function (12.45) behaves like in equation
(12.46) resulting in a finite correlation length
the correlation function (12.45) behaves like in equation
(12.46) resulting in a finite correlation length  . The correlation
length
diverges as we approach the critical temperature, and its asymptotic behavior in
this limit is given by the scaling relation
. The correlation
length
diverges as we approach the critical temperature, and its asymptotic behavior in
this limit is given by the scaling relation
 | (13.6) |
Then the correlation function behaves according to (12.47)
 | (13.7) |
Scaling behavior is also found for the specific heat  , the magnetization
, the magnetization
 and the magnetic susceptibility
and the magnetic susceptibility  according to the relations
according to the relations
whereas the magnetization for  and nonzero magnetic field
and nonzero magnetic field  behaves
like
behaves
like
 | (13.11) |
The exponents in the above scaling relations are called critical exponents or
scaling exponents. They take universal values, i.e. they don’t depend on the details
of the lattice construction or of the interaction. A whole class of such models
with different microscopic definitions have the exact same long distance
behavior !
The systems in the same universality class need to share the same symmetries and
dimensionality of space and the fact that the interaction is of short range. In the
particular model that we study, these exponents take the so called Onsager
exponent values
 | (13.12) |
Theses exponents determine the non analytic behavior of the corresponding
functions in the thermodynamic limit. Non analyticity cannot arise in the finite
 model. The partition function (13.4) is a sum of a finite number of
analytic terms, which of course result in an analytic function. The non
analytic behavior manifests in the
model. The partition function (13.4) is a sum of a finite number of
analytic terms, which of course result in an analytic function. The non
analytic behavior manifests in the  limit, where the finite
limit, where the finite  analytic functions converge to a non analytic one. The loss of analyticity is
related to the appearance of long distance correlations between the spins
and the scaling of the correlation length according to equation (13.6)
.
analytic functions converge to a non analytic one. The loss of analyticity is
related to the appearance of long distance correlations between the spins
and the scaling of the correlation length according to equation (13.6)
.
The two phases, separated by the phase transition, are identified by the
different values of an order parameter. Each phase is characterized by the
appearance or the breaking of a symmetry. In the Ising model, the order
parameter is the magnetization and the symmetry is the  symmetry
represented by the transformation
symmetry
represented by the transformation  . The magnetization is zero in the
disordered, high temperature phase and non zero in the ordered, low temperature
phase. This implies that the magnetization is a non analytic function of the
temperature .
. The magnetization is zero in the
disordered, high temperature phase and non zero in the ordered, low temperature
phase. This implies that the magnetization is a non analytic function of the
temperature .
Universality and scale invariance appear in the  limit. In our case, this
occurs by tuning only one parameter, the temperature, to its critical value. A
unique, dynamical, length scale emerges from the correlation function, the
correlation length
limit. In our case, this
occurs by tuning only one parameter, the temperature, to its critical value. A
unique, dynamical, length scale emerges from the correlation function, the
correlation length  . Scale invariance manifests when the correlation length
becomes much larger than the microscopic length scale
. Scale invariance manifests when the correlation length
becomes much larger than the microscopic length scale  when
when  . In the
critical region, all quantities which are functions of the distance become functions
only of the ratio
. In the
critical region, all quantities which are functions of the distance become functions
only of the ratio  . Everything depends on the long wavelength fluctuations
required by the symmetry of the order parameter and all models in the same
universality class have the same long distance behavior. This way one
can study only the simplest model within a universality class in order to
deduce the large distance/long wavelength properties of all systems in the
class.
. Everything depends on the long wavelength fluctuations
required by the symmetry of the order parameter and all models in the same
universality class have the same long distance behavior. This way one
can study only the simplest model within a universality class in order to
deduce the large distance/long wavelength properties of all systems in the
class.
13.2 Metropolis
Consider a square lattice with  sites on each side so that
sites on each side so that  is
the number of lattice sites (vertices) and
is
the number of lattice sites (vertices) and  is the number of links (bonds)
between the sites. The relation
is the number of links (bonds)
between the sites. The relation  holds because we choose helical
boundary conditions as shown in figure 13.6. The choice of boundary
conditions will be discussed later. On each site
holds because we choose helical
boundary conditions as shown in figure 13.6. The choice of boundary
conditions will be discussed later. On each site  we have one degree of
freedom, the “spin”
we have one degree of
freedom, the “spin”  which takes on two values
which takes on two values  . We consider the
case of zero magnetic field
. We consider the
case of zero magnetic field  , therefore the Hamiltonian is given
by
, therefore the Hamiltonian is given
by
 | (13.13) |
The sum  is a sum over the links
is a sum over the links  , corresponding to the pairs of sites
, corresponding to the pairs of sites
 . Then
. Then  since each bond is counted twice in the
second sum. The partition function is
since each bond is counted twice in the
second sum. The partition function is
![∑ ∑ ∑ ∑ ∑
Z = ... e−βH[{si}] ≡ eβ ⟨ij⟩sisj.
s1=±1 s2= ±1 sN=±1 {si}](main_latex4733x.png) | (13.14) |
Our goal is to collect a sample of states that is distributed according to the
Boltzmann distribution (12.4) . This will be constructed via a Markov process
according to the discussion in section 12.6. Sampling is made according to (12.53)
and the expectation values are estimated from the sample using (12.54) . At
each step the next state is chosen according to (12.60) , and for large
enough sample, or “time steps”, the sample is approximately in the desired
distribution.
Suppose that the system is in a
state
 . According to (12.66) , the probability that in the next step the system goes
into the state
. According to (12.66) , the probability that in the next step the system goes
into the state  is
is
 | (13.15) |
where  is the selection probability of the state
is the selection probability of the state  when the system is in
the state
when the system is in
the state  and
and  is the acceptance ratio, i.e. the probability that the
system jumps into the new state. If the detailed balance condition (12.60)
is the acceptance ratio, i.e. the probability that the
system jumps into the new state. If the detailed balance condition (12.60)
 | (13.16) |
is satisfied, then the distribution of the sample will converge to (12.4)
 . In order that the system changes states often enough, the
probabilities
. In order that the system changes states often enough, the
probabilities  should be of order one and the differences in the
energy
should be of order one and the differences in the
energy  should not be too large. This means that the product of
the temperature with the energy difference should be a number of order
one or less. One way to accomplish this is to consider states that differ
by the value of the spin on only one site
should not be too large. This means that the product of
the temperature with the energy difference should be a number of order
one or less. One way to accomplish this is to consider states that differ
by the value of the spin on only one site  . Since the
energy (13.13) is a local quantity, the change in energy will be small. More
specifically, if each site has
. Since the
energy (13.13) is a local quantity, the change in energy will be small. More
specifically, if each site has  nearest neighbors, the change of the spin on
site
nearest neighbors, the change of the spin on
site  results in a change of sign for
results in a change of sign for  terms
terms  in (13.13) . The
change in the energy for each bond is
in (13.13) . The
change in the energy for each bond is  . If the state
. If the state  is given by
is given by
 and the state
and the state  by
by  (i.e. all the spins
are the same except the spin
(i.e. all the spins
are the same except the spin  which changes sign), the energy difference will
be
which changes sign), the energy difference will
be
 | (13.17) |
If the site  is randomly chosen then
is randomly chosen then
 | (13.18) |
and the algorithm is ergodic. Then we have that
 | (13.19) |
A simple choice for satisfying this condition is (12.61)
 | (13.20) |
In order to maximize the acceptance ratios we have to take  .
Remember that we should have
.
Remember that we should have  and
and  . Therefore
. Therefore
 | (13.21) |
Figure 13.4 depicts the dependence of  on the change in energy for
different values of
on the change in energy for
different values of  . We observe that this probability is small even
for zero energy change and we expect this method not to perform very
well.
. We observe that this probability is small even
for zero energy change and we expect this method not to perform very
well.
It is much more efficient to use the algorithm proposed by Nicolas Metropolis
et. al. 1953 [59] which is given by (12.63)
 | (13.22) |
According to this relation, when a change in the states lowers the energy, the
change is always accepted. When it increases the energy, the change is
accepted with a probability less than one. As we can see in figure 13.4,
this process accepts new states much more frequently than the previous
algorithm.
The Metropolis algorithm is very widely used. It is applicable to any system, it is
simple and efficient. We note that the choice to change the spin only locally is not
a restriction put by the metropolis algorithm. There exist efficient algorithms that
make non local changes to the system’s configuration that (almost) conserve the
Hamiltonian
and, consequently, the acceptance ratios are satisfactorily large.
13.3 Implementation
The first step in designing a code is to define the data structure. The
degrees of freedom are the spins  which are defined on
which are defined on  lattice
sites. The most important part in designing the data structure in a lattice
simulation is to define the neighboring relations among the lattice sites
in the computer memory and this includes the implementation of the
boundary conditions. A bad choice of boundary conditions will make
the effect of the boundary on the results to be large and increase the
finite size effects. This will affect the speed of convergence of the results
to the thermodynamic limit, which is our final goal. The most popular
choice is the toroidal or periodic boundary conditions. A small variation of
these lead to the so called helical boundary conditions, which will be
our choice because of their simplicity. Both choices share the fact that
each site has the same number of nearest neighbors, which give the same
local geometry everywhere on the lattice and minimize finite size effects
due to the boundary. In contrast, if we choose fixed or free boundary
conditions on the sides of the square lattice, the boundary sites have
a smaller number of nearest neighbors than the ones inside the lattice.
lattice
sites. The most important part in designing the data structure in a lattice
simulation is to define the neighboring relations among the lattice sites
in the computer memory and this includes the implementation of the
boundary conditions. A bad choice of boundary conditions will make
the effect of the boundary on the results to be large and increase the
finite size effects. This will affect the speed of convergence of the results
to the thermodynamic limit, which is our final goal. The most popular
choice is the toroidal or periodic boundary conditions. A small variation of
these lead to the so called helical boundary conditions, which will be
our choice because of their simplicity. Both choices share the fact that
each site has the same number of nearest neighbors, which give the same
local geometry everywhere on the lattice and minimize finite size effects
due to the boundary. In contrast, if we choose fixed or free boundary
conditions on the sides of the square lattice, the boundary sites have
a smaller number of nearest neighbors than the ones inside the lattice.
One choice for mapping the lattice sites into the computer memory is to use
their coordinates  ,
,  . Each spin is stored in an array s(L,L).
For a site s(i,j) the four nearest neighbors are s(i
. Each spin is stored in an array s(L,L).
For a site s(i,j) the four nearest neighbors are s(i 1,j), s(i,j
1,j), s(i,j 1). The
periodic boundary conditions are easily implemented by adding
1). The
periodic boundary conditions are easily implemented by adding  to i,j each
time they become less than one or greater than
to i,j each
time they become less than one or greater than  . This is shown in figures 13.5
and 13.30.
. This is shown in figures 13.5
and 13.30.
The elements of the array s(L,L) are stored linearly into the computer
memory. The element s(i,j) is at a “distance” (j-1)*L+i array positions from
s(1,1) and accessing its value involves an, invisible to the programmer,
multiplication. Using helical boundary conditions this multiplication can be
avoided. The positions of the lattice sites are now given by one number
 , as shown in figures 13.6 and 13.31. The spins are stored in
memory in a one dimensional array s(N) and the calculation of the nearest
neighbors of a site s(i) is easily done by taking the spins s(i
, as shown in figures 13.6 and 13.31. The spins are stored in
memory in a one dimensional array s(N) and the calculation of the nearest
neighbors of a site s(i) is easily done by taking the spins s(i 1) and
s(i
1) and
s(i L). The simplicity of the helical boundary conditions is based
on the fact that, for the nearest neighbors of sites on the sides of the
square, all we have to do is to make sure that the index i stays within
the accepted range 1
L). The simplicity of the helical boundary conditions is based
on the fact that, for the nearest neighbors of sites on the sides of the
square, all we have to do is to make sure that the index i stays within
the accepted range 1 i
i  N. This is easily done by adding or
subtracting
N. This is easily done by adding or
subtracting  when necessary. Therefore in a program that we want to
calculate the four nearest neighbors nn of a site i, all we have to do is:
when necessary. Therefore in a program that we want to
calculate the four nearest neighbors nn of a site i, all we have to do is:
nn=i+1;if(nn.gt.N)nn=nn-N
nn=i-1;if(nn.lt.1)nn=nn+N
nn=i+L;if(nn.gt.N)nn=nn-N
nn=i-L;if(nn.lt.1)nn=nn+N
We will choose helical boundary conditions for their simplicity and efficiency in calculating
nearest neighbors .
The dynamics of the Monte Carlo evolution is determined by the initial state
and the Metropolis algorithm. A good choice of initial configuration can be
important in some cases. It could lead to fast or slow thermalization, or even to
no thermalization at all. In the model that we study it will not play an important
role, but we will discuss it because of its importance in the study of other systems.
We may choose a “cold” ( - all spins aligned) or a “hot” (
- all spins aligned) or a “hot” ( - all
spins are equal to
- all
spins are equal to  with equal probability
with equal probability  ) initial configuration.
For large lattices, it is desirable to start in one of these states and then
lower/increase the temperature in small steps. Each time that the temperature is
changed, the spin configuration is saved and used in the next simulation.
) initial configuration.
For large lattices, it is desirable to start in one of these states and then
lower/increase the temperature in small steps. Each time that the temperature is
changed, the spin configuration is saved and used in the next simulation.
Ergodicity and thermalization must be checked by performing independent
simulations
and verify that we obtain the same results. Similarly, independent simulations
starting from different initial states must also be checked that yield the same
results.
Consider each step in the Markov process defined by the Metropolis algorithm.
Assume that the system is in the state  and consider the
transition to a new state
and consider the
transition to a new state  which differs only by the
value of the spin
which differs only by the
value of the spin  (spin flip), whereas all the other spins are the
same:
(spin flip), whereas all the other spins are the
same: 
 . The energy difference between the two states is
. The energy difference between the two states is
where the second line is obtained after the cancellation of the common terms in the
sums. In the third line we used the relation  , which you can prove
easily by examining the cases
, which you can prove
easily by examining the cases  separately. The important property of
this relation is that it is local since it depends only on the nearest neighbors. The
calculation of the energy difference
separately. The important property of
this relation is that it is local since it depends only on the nearest neighbors. The
calculation of the energy difference  is fast and is always a number of order
one .
is fast and is always a number of order
one .
The Metropolis condition is easily implemented. We calculate the sum in the
parenthesis of the last line of equation (13.23) and obtain the energy difference
 . If the energy decreases, i.e.
. If the energy decreases, i.e.  , the new state
, the new state  is
accepted and “we flip the spin”. If the energy increases, i.e.
is
accepted and “we flip the spin”. If the energy increases, i.e.  , then
the acceptance ratio is
, then
the acceptance ratio is  . In order to accept the new
state with this probability we pick a random number uniformly distributed in
. In order to accept the new
state with this probability we pick a random number uniformly distributed in
 . The probability that this number is
. The probability that this number is  is equal
to
is equal
to
 . Therefore if
. Therefore if  the change is accepted. If
the change is accepted. If
 the change is rejected and the system remains in the same state
the change is rejected and the system remains in the same state
 .
.
A small technical remark is in order: The possible values of the sum
 and these are the only values that enter in the
calculation of
and these are the only values that enter in the
calculation of  . Moreover, only the values that increase the energy, i.e.
. Moreover, only the values that increase the energy, i.e.
 are of interest to us. Therefore we only need two values of
are of interest to us. Therefore we only need two values of  , which
depend only on the temperature. These can by calculated once and for all in
the initialization phase of the program, stored in an array and avoid the
repeated calculation of the exponential
, which
depend only on the temperature. These can by calculated once and for all in
the initialization phase of the program, stored in an array and avoid the
repeated calculation of the exponential  which is expensive.
which is expensive.
In our program we also need to implement the calculation of the observables
that we want to measure. These are the energy (13.13)
 | (13.24) |
and the magnetization
 | (13.25) |
Beware of the absolute value in the last equation! The Hamiltonian
 has a
has a  symmetry because it is symmetric under reflection
of all the spins. The probability of appearance of a state depends only
on the value of
symmetry because it is symmetric under reflection
of all the spins. The probability of appearance of a state depends only
on the value of  , therefore two configurations with opposite spin are
equally probable. But such configurations have opposite magnetization,
therefore the average magnetization
, therefore two configurations with opposite spin are
equally probable. But such configurations have opposite magnetization,
therefore the average magnetization  will be zero due to this
cancellation .
will be zero due to this
cancellation .
We can measure the energy and the magnetization in two ways. The first one
is by updating their values each time a Metropolis step is accepted. This is easy
and cheap since the difference in the sum in equations (13.24) and (13.25)
depends only on the value of the spin  and its nearest neighbors. The energy
difference is already calculated by (13.23) whereas the difference in the
magnetization in (13.25) is given by
and its nearest neighbors. The energy
difference is already calculated by (13.23) whereas the difference in the
magnetization in (13.25) is given by
 | (13.26) |
The second way is by calculating the full sums in (13.24) and
(13.25) every time that we want to take a measurement. The optimal
choice depends on how often one obtains a statistically independent
measurement .
If the average acceptance ratio is  , then the calculation of the magnetization
using the first method requires
, then the calculation of the magnetization
using the first method requires  additions per
additions per  Monte Carlo steps,
whereas the second one requires
Monte Carlo steps,
whereas the second one requires  additions per measurement.
additions per measurement.
We use the normalization
 | (13.27) |
which gives the energy per link. We have that  , where
, where  for
the ground state in which all
for
the ground state in which all  links have energy equal to
links have energy equal to  . The
magnetization per site is
. The
magnetization per site is
 | (13.28) |
We have that  , where
, where  for
for  (perfect disorder) and
(perfect disorder) and
 for the ground state at
for the ground state at  (perfect order). We call
(perfect order). We call  the
order parameter since its value determines the phase that the system is
in.
the
order parameter since its value determines the phase that the system is
in.
The specific heat is given by the fluctuations of the energy
 | (13.29) |
and the magnetic susceptibility by the fluctuations of the magnetization
 | (13.30) |
In order to estimate the amount of data necessary for an accurate
measurement of these quantities, we consider the fact that for  independent
measurements the statistical error drops as
independent
measurements the statistical error drops as  . The problem of
determining how often we have independent measurements is very important and
it will be discussed in detail later in this chapter.
. The problem of
determining how often we have independent measurements is very important and
it will be discussed in detail later in this chapter.
13.3.1 The Program
In this section we discuss the
program
that implements the Monte Carlo simulation of the Ising model. The code in this
section can be found in the accompanying software of this chapter in the directory
Ising_Introduction.
In the design of the code, we follow the philosophy of modular programming.
Different independent sections of the program will be coded in different
files. This makes easier the development, maintenance and correction of
the code by one or a team of programmers. A header file contains the
definitions which are common for the code in one or more files. Then, all the
parameters and common blocks are in one place and they are easier to
modify for all program units in a unified way, therefore avoiding errors. In
our case we have only one such file, named include.inc, whose code
will be included in the beginning of each program unit using an include
statement:
!============== include.inc ==================
implicit none
integer,parameter :: L = 12
integer,parameter :: N = L*L
integer,parameter :: XNN = 1, YNN = L
integer,dimension(N) :: s
real(8),dimension(0:4) :: prob
real(8) :: beta
common /lattice/ s
common /parameters/ beta,prob
!function definitions:
real(8) :: drandom
integer :: seed
common /randoms/ seed
The lattice size  is a constant parameter, whereas the arrays and variables
encoding the spins and the simulation parameters are put in common
blocks. The array s(N) stores the spin of each lattice site which take
values
is a constant parameter, whereas the arrays and variables
encoding the spins and the simulation parameters are put in common
blocks. The array s(N) stores the spin of each lattice site which take
values  . The variable beta is the temperature
. The variable beta is the temperature  and the array
prob(0:4) stores the useful values of the acceptance ratios
and the array
prob(0:4) stores the useful values of the acceptance ratios  according to the discussion on page 1322. The function drandom() is the one
discussed in section 11.1, which generates pseudorandom numbers uniformly
distributed in the interval
according to the discussion on page 1322. The function drandom() is the one
discussed in section 11.1, which generates pseudorandom numbers uniformly
distributed in the interval  -
-  and
and  excluded. The parameters XNN
and YNN are used for computing the nearest neighbors in the X and Y
directions according to the discussion of section 13.3 on helical boundary
conditions. For example, for an internal site i, i+XNN is the nearest neighbor
in the
excluded. The parameters XNN
and YNN are used for computing the nearest neighbors in the X and Y
directions according to the discussion of section 13.3 on helical boundary
conditions. For example, for an internal site i, i+XNN is the nearest neighbor
in the  direction and i-YNN is the nearest neighbor in the
direction and i-YNN is the nearest neighbor in the  direction.
direction.
The main program is in the file main.f90 and drives the simulation:
!============== main.f90 ==================
program Ising2D
include ’include.inc’
integer :: start !start= 0 (cold)/1 (hot)
integer :: isweep, nsweep
nsweep = 1000
beta=0.21D0;seed=9873;start=1;
call init(start)
do isweep = 1, nsweep
call met
call measure
end do
end program Ising2D
In the beginning we set the simulation parameters. The initial configuration is
determined by the value of start. If start=0, then it is a cold configuration and
if start=1, then it is a hot configuration. The temperature is set by the value of
beta and the number of sweeps of the lattice by the value of nsweep. One sweep
of the lattice is defined by N attempted spin flips. The flow of the simulation is
determined by the initial call to init, which performs all initialization tasks, and
the subsequent calls to met and measure, which perform nsweep Metropolis
sweeps and measurements respectively.
One level down lies the subroutine init. The value of start is passed through
its argument so that the desired initial state is set:
!============== init.f90 ==================
! file init.f90
! init(start): start = 0: cold start
! start = 1: hot start
!=============================================
subroutine init(start)
include ’include.inc’
integer :: start
integer :: i
!----------------------
!initialize probabilities for E_\nu > E_mu
prob=0.0D0
do i=2,4,2 !i = dE/2 = (E_nu-E_mu)/2=2,4
prob(i) = exp(-2.0D0*beta*i)
enddo
!initial configuration:
select case(start)
case(0)!cold:
s = 1 !all s(i) = 1
case(1)!hot:
do i=1,N
if(drandom() .lt. 0.5D0)then
s(i) = 1
else
s(i) = -1
endif
enddo
case default
print *,’init: start= ’,start,’ not valid. Exiting...’
stop
end select
end subroutine init
At first the array prob(0:4) is initialized to the values of the acceptance ratios


 . Those probabilities are going to be
used when
. Those probabilities are going to be
used when  and the possible values are obtained when this
expression takes the values 2 and 4. These are the values stored in the array
prob(0:4), and we remember that the index of the array is the expression
and the possible values are obtained when this
expression takes the values 2 and 4. These are the values stored in the array
prob(0:4), and we remember that the index of the array is the expression
 , when it is positive.
, when it is positive.
The initial spin configuration is determined by the integer start. Using the
select case block allows us to add more options in the future. When start=0
all spins are set equal to 1, whereas when start=1 each spin’s value is set
to  with equal probability. The probability that drandom()<0.5
is
with equal probability. The probability that drandom()<0.5
is
 in which case we set s(i)=1, otherwise (probability
in which case we set s(i)=1, otherwise (probability  ) we set
s(i)=-1.
) we set
s(i)=-1.
The heart of the program is the subroutine met() which attempts N
Metropolis steps. It picks a random site N times and asks the question whether to
perform a spin flip. This is done using the Metropolis algorithm by calculating the
change in the energy of the system before and after the change of the spin value
according to (13.23) :
!============== met.f90 ==================
subroutine met()
include ’include.inc’
integer :: i,k
integer :: nn,snn,dE
do k=1,N
!pick a random site:
i = INT(N*drandom())+1
!snn=sum of neighboring spins:
snn = 0
nn=i+XNN;if(nn.gt.N)nn=nn-N;snn = snn + s(nn)
nn=i-XNN;if(nn.lt.1)nn=nn+N;snn = snn + s(nn)
nn=i+YNN;if(nn.gt.N)nn=nn-N;snn = snn + s(nn)
nn=i-YNN;if(nn.lt.1)nn=nn+N;snn = snn + s(nn)
!dE=change in energy/2:
dE=snn*s(i)
!flip:
if(dE.le.0)then
s(i) = -s(i) !accept
else if(drandom() < prob(dE))then
s(i) = -s(i) !accept
endif
enddo !do k=1,N: end sweep
end subroutine met
The line
i = INT(N*drandom())+1
picks a site i=1,...,N with equal probability. It is important that the value
i=N+1 never appears, something that happens if drandom()=1.0. This value has
been excluded according to the discussion in section 11.1.
Next, we calculate the sum  in (13.23) . The nearest
neighbors of the site i have to be determined and this happens in the
lines
in (13.23) . The nearest
neighbors of the site i have to be determined and this happens in the
lines
snn = 0
nn=i+XNN;if(nn.gt.N)nn=nn-N;snn = snn + s(nn)
nn=i-XNN;if(nn.lt.1)nn=nn+N;snn = snn + s(nn)
nn=i+YNN;if(nn.gt.N)nn=nn-N;snn = snn + s(nn)
nn=i-YNN;if(nn.lt.1)nn=nn+N;snn = snn + s(nn)
The variable delta is set equal to the product (13.23)  . If it
turns out to be negative, then the change in energy is negative and the spin flip is
accepted. If it turns out to be positive, then we apply the criterion set by (13.22)
by using the array prob(delta), which has been set in the subroutine init. The
probability that drandom()<prob(delta) is equal to prob(delta), in which case
the spin flip is accepted. In all other cases, the spin flip is rejected and s(i)
remains the same.
. If it
turns out to be negative, then the change in energy is negative and the spin flip is
accepted. If it turns out to be positive, then we apply the criterion set by (13.22)
by using the array prob(delta), which has been set in the subroutine init. The
probability that drandom()<prob(delta) is equal to prob(delta), in which case
the spin flip is accepted. In all other cases, the spin flip is rejected and s(i)
remains the same.
After each Metropolis sweep we perform a measurement. The code is minimal
and simply prints the value of the energy and the magnetization to the stdout.
The analysis is assumed to be performed by external programs. This way we keep
the production code simple and store the raw data for a detailed and flexible
analysis. The printed values of the energy and the magnetization will be used as
monitors of the progress of the simulation, check thermalization and measure
autocorrelation times. Plots of the measured values of an observable as a
function of the Monte Carlo “time” are the so called “time histories”. Time
histories of appropriately chosen observables should always be viewed and
used in order to check the progress and spot possible problems in the
simulation.
The subroutine measure calculates the total energy and magnetization
(without the absolute value) by a call to the functions E() and M(), which apply
the formulas (13.24) and (13.25) .
!============== measure.f90 ==================
subroutine measure()
include ’include.inc’
integer :: E,M
print *, E(),M()
end subroutine measure
!=====================
integer function E()
include ’include.inc’
integer en,sum,i,nn
en = 0
do i=1,N
!Sum of neighboring spins: only forward nn necessary in the sum
sum = 0
nn=i+XNN;if(nn.gt.N)nn=nn-N;sum = sum + s(nn)
nn=i+YNN;if(nn.gt.N)nn=nn-N;sum = sum + s(nn)
en=en+sum*s(i)
enddo
e = -en
end function E
!=====================
integer function M()
include ’include.inc’
M=SUM(s)
end function M
The compilation of the code is done with the command
> gfortran main.f90 met.f90 init.f90 measure.f90 drandom.f90 \
-o is
which results in the executable file is:
> ./is > out.dat
> less out.dat
-52 10
-48 40
-64 44
-92 64
......
The output of the program is two columns with the values of the total energy
and magnetization (without the absolute value). In order to construct their time
histories we give the gnuplot commands:
gnuplot> plot "out.dat" using 1 with lines
gnuplot> plot "out.dat" using 2 with lines
gnuplot> plot "out.dat" using (($2>0)?$2:-$2) with lines
The last line calculates the absolute values of the second column. The C-like
construct ($2>0)?$2:-$2 checks whether the expression ($2>0) is true. If it is,
then it returns $2, otherwise it returns -$2.
13.3.2 Towards a Convenient User Interface
In this section we will improve the code, mostly at the user interface level. This is
a nice exercise on the interaction of the programming language with the shell and
the operating system. The code presented can be found in the accompanying
software of this chapter in the directory Ising_Metropolis.
An annoying feature of the program discussed in the previous section is that
the simulation parameters are hard coded and the user needs to recompile the
program each time she changes them. This is not very convenient if she has to do
a large number of simulations. Another notable change that needs to be
made in the code is that the final configuration of the simulation must be
saved in a file, in order to be read as an initial configuration by another
simulation.
One of the parameters that the user might want to set interactively at
run time is the size of the lattice L. But this parameter determines the
required memory for the array s(N). Therefore we have to use dynamic
memory allocation for this array using the intrinsic function ALLOCATE.
Another problem is that the array s(N) needs to be accessible by several
parts of the program and allocatable arrays cannot be put in a common
block. Another mechanism for sharing data among different functions
and subroutines is the use of modules. This is the preferable method of
doing it in modern Fortran programs where the use of common blocks
is discouraged. The shared data needs to be put between the following
statements:
module global_data
implicit none
SAVE
....
end module global_data
In place of the ... we can put variable declarations. We use the statement SAVE
so that their values are saved between function and subroutine calls. The module
has a name which in our case is global_data. Each program unit that
needs to have access to its data needs to start with the statement use
global_data:
subroutine share_global_data
use global_data
implicit none
....
end subroutine share_global_data
In the file global_data.f90 we put all the global variables as follows:
module global_data
implicit none
SAVE
integer :: L
integer :: N
integer :: XNN, YNN
integer,allocatable :: s(:)
real(8),dimension(0:4) :: prob
real(8) :: beta
integer :: nsweep,start
integer :: seed,ranlux_level
real(8) :: acceptance
character(1024) :: prog
end module global_data
The array s(:) is allocatable and its storage space will be allocated in the
subroutine init. The variables L, N, XNN and YNN are not parameters anymore
and their values will also be set in init. The new variables are acceptance which
computes the fraction of accepted spin flips in a simulation, ranlux_level which
determines the luxury level of RANLUX and prog which stores the command line
name of the program that runs the simulation.
The main program has very few changes:
!============== main.f90 ==================
program Ising2D
use global_data
implicit none
integer :: isweep
call init
do isweep = 1, nsweep
call met
call measure
end do
call endsim
end program Ising2D
Notice the line use global_data which gives access to the data in the module
global_data. This is the first line of all program units. The subroutine endsim
finishes off the simulation. Its most important function is to store the final
configuration to a file for later use.
The subroutine init is changed quite a bit since it performs most of the
functions that have to do with the user interface:
!============== init.f90 ==================
! start = 0: cold start
! start = 1: hot start
! start = 2: use old configuration
!=============================================
subroutine init
use global_data
implicit none
integer :: i,chk
real(8) :: obeta=-1.0D0,r
integer :: OL=-1
character(1024) :: buf
integer,parameter :: f_in=17 !file unit
integer :: seeds(25)
!----------------------
!Define parameters from options:
L=-1;beta=-1.0D0;nsweep=-1;start=-1;seed=-1
ranlux_level=3
call get_the_options
if(start.EQ.0 .OR. start.EQ.1)then
if(L < 0 )call locerr(’L has not been set.’)
if(seed < 0 )call locerr(’seed has not been set.’)
if(beta < 0.0D0)call locerr(’beta has not been set.’)
!Derived parameters:
N=L*L;XNN=1;YNN=L
!Allocate memory for the spins:
ALLOCATE(s(N),STAT=chk)
if(chk > 0)call locerr(’allocation failure for s(N)’)
endif !if(start.EQ.0 .OR. start.EQ.1)
if(start < 0)call locerr(’start has not been set.’)
if(nsweep < 0)call locerr(’nsweep has not been set.’)
!----------------------
!initialize probabilities for E_\nu > E_mu
prob=0.0D0
do i=2,4,2 !i = dE/2 = (E_nu-E_mu)/2=2,4
prob(i) = exp(-2.0D0*beta*i)
enddo
acceptance = 0.0D0
!--------------------------------------------
!initial configuration: cold(0),hot(1),old(2)
!--------------------------------------------
select case(start)
!--------------------------------------------
case(0)!cold:
call simmessage(6)
call RLUXGO(ranlux_level,seed,0,0)
s = 1 !all s(i) = 1
!--------------------------------------------
case(1)!hot:
call simmessage(6)
call RLUXGO(ranlux_level,seed,0,0)
do i=1,N
call ranlux(r,1)
if(r .lt. 0.5D0)then
s(i) = 1
else
s(i) = -1
endif
enddo
!--------------------------------------------
case (2)!old:
if(beta < 0.0D0)call locerr(’beta has not been set.’)
open(f_in,file=’conf’,status=’OLD’,ERR=101)
read(f_in,*)buf !read in a comment line
read(f_in,’(A4,I5,A4,I5,A6,G28.17,A6,25I16)’)&
buf,OL,buf,OL,buf,beta,buf,seeds
if(L < 0 ) L = OL !if L has not been set, read from file
if(L /= OL) & ! /= the same as .NE. (not equal)
call locerr(’L different from the one read from conf.’)
N=L*L;XNN=1;YNN=L
!Allocate memory for the spins:
ALLOCATE(s(N),STAT=chk);
if(chk > 0)call locerr(’allocation failure for s(N)’)
call simmessage(6)
print ’(A)’,’# Reading configuration from file conf’
do i=1,N
read(f_in,*,END=102) s(i)
if(s(i) /= 1 .AND. s(i) /= -1)&
call locerr(’wrong value of spin’)
enddo
close(f_in)
if(seed < 0) then !initialize from seeds read from file:
call RLUXIN(seeds)
else !option seed sets new seed:
call RLUXGO(ranlux_level,seed,0,0)
endif
!--------------------------------------------
case default
print *,’init: start= ’,start,’ not valid. Exiting...’
stop 1
end select
!--------------------------------------------
return
!here we put error messages:
101 call locerr(’Configuration file conf not found.’)
102 call locerr(’File conf ended before reading all spins.’)
end subroutine init
In the beginning, the simulation parameters that are to be determined by the user
are given invalid default values. This way they are flagged as not been set. The
subroutine
get_the_options sets the parameters to the values that the user passes through
the command line:
L=-1;beta=-1.0D0;nsweep=-1;start=-1;seed=-1
call get_the_options
Upon return of get_the_options, one has to check if all the parameters have
been set to acceptable values. For example, if the user has forgotten to set the
lattice size L, the call to the subroutine locerr stops the program and prints the
error message passed through its argument:
if(L < 0 )call locerr(’L has not been set.’)
When the value of N is calculated from L, the program allocates memory for the
array s(N):
N=L*L
ALLOCATE(s(N),STAT=chk)
if(chk > 0)call locerr(’allocation failure for s(N)’)
When memory allocation is successful, the variable chk is set to 0 by ALLOCATE.
Otherwise we stop the program with a call to locerr.
Using the construct SELECT CASE(start) we set the initial configuration of
the simulation. A value of start=0 sets all spins equal to 1. The subroutine
simmmessage(f_unit) prints important information about the simulation to the
unit f_unit. The random number generator RANLUX is initialized with a call to
RLUXGO according to the discussion in section 11.2, page 1202. The global variable
ranlux_level is set to 3 by default, but the user can change it from the
command line (see get_the_options). If start=0 the initial configuration is
hot.
If start=2 we attempt to read a configuration stored in a file named conf.
The format of the file is strictly set by the way we print the configuration in
the subroutine endsim. If the file does not exist, the argument ERR=101
transfers the control of the program to the labeled statement with label
101. This is near the end of the program and stops the program with a
call to locerr. In order to read the configuration properly we need to
know the format of the data in the file conf which is, more or less, as
follows:
# Configuration of 2d Ising model on square lattice....
Lx= 12 Ly= 12 beta= 0.21 seed= 3718479 5267541 12092770 ....
-1
1
1
1
-1
.....
All comments of the first line are discarded in the character variable buf. The
parameters L and beta of the stored configuration are stored in temporary
variables OL, obeta, so that they can be compared with the values set by the
user.
If the user provides a seed, then her seed will be used for seeding.
Otherwise RANLUX is initialized to the state read from the file conf. Both
choices are desirable in different cases: If the user wants to split a long
simulation into several short runs, then each time she wants to restart the
random number generator at exactly the same state. If she wants to use
the same configuration in order to produce many independent results,
then RANLUX has to produce different sequences of random numbers each
time .
This feature is coded in the lines:
if(seed < 0) then !initialize from seeds read from file:
call RLUXIN(seeds)
else !option seed sets new seed:
call RLUXGO(ranlux_level,seed,0,0)
endif
When reading the spins, we have to make sure that they take only
the legal values  and that the data is enough to fill the array
s(N) .
Reading enough data is checked by the READ argument END=102. If the READ
statement attempts to read past the end of the file conf, then the control of the
program is transferred to the labeled statement with label 102. This will happen,
e.g. if we attempt to read from a corrupted file.
and that the data is enough to fill the array
s(N) .
Reading enough data is checked by the READ argument END=102. If the READ
statement attempts to read past the end of the file conf, then the control of the
program is transferred to the labeled statement with label 102. This will happen,
e.g. if we attempt to read from a corrupted file.
The subroutine endsim saves the last configuration in the file conf and can be
found in the file end.f90:
!============== end.f90 ==================
subroutine endsim()
use global_data
implicit none
integer,parameter :: f_out = 17
integer :: i,seeds(25)
call RLUXUT(seeds)
call rename(’conf’,’conf.old’)
open(unit=f_out,file=’conf’)
write(f_out,’(A)’)&
’# Configuration of 2d Ising model on square lattice...’
write(f_out,’(A4,I5,A4,I5,A6,G28.17,A6,25I16)’)&
’Lx= ’,L,’ Ly= ’,L,’ beta= ’,beta,’ seed= ’,seeds
do i=1,N
write(f_out,’(I3)’)s(i)
enddo
close(f_out)
print ’(A,F7.3)’,’# acceptance= ’,&
acceptance/DBLE(N)/DBLE(nsweep)
end subroutine endsim
The state of the random number generator RANLUX is saved by a call to RLUXUT
which stores the necessary information in the array seeds. The call to the
subroutine RENAME renames the file conf (if it exists) to the backup file conf.old.
The format (A4, I5, A4, I5, A6, G28.17, A6, 25I16) has to be obeyed
strictly during the output, as well as during the input of the configuration in the
subroutine init.
The subroutine get_the_options() reads the parameters, passed through
options from the command line. The choice to use options for passing parameters
to the program has the advantage that they can be passed optionally and in any
order desired. Let’s see how they work. Assume that the executable file is named
is. The command
> ./is -L 10 -b 0.44 -s 1 -S 5342 -n 1000
will run the program after setting L=10 (-L 10), beta=0.44 (-b 0.44), start=1
(-s 1), seed=5342 (-S 5342) and nsweep=1000 (-n 1000). The -L, -b, -s,
-S, -n are options or switches and can be put in any order in the arguments of
the command line. The arguments following an option are the values
passed to the corresponding variables. Options can also be used without
arguments, in which case a common use is to make the command function
differently .
In our case, the option -h is an option without an argument which makes the
program to print a usage message and exit without running the simulation:
> ./is -h
Usage: ./is [options]
-L: Lattice length (N=L*L)
-b: beta
-s: start (0 cold, 1 hot, 2 old config.)
-S: seed
-n: number of sweeps and measurements
-u: seed from /dev/urandom
-r: ranlux_level
Monte Carlo simulation of 2d Ising Model. Metropolis is used by
default. Using the options, the parameters of the simulations
must be set for a new run (start=0,1). If start=2, a
configuration is read from the file conf.
This is a way to provide a short documentation on the usage of a program.
Let’s see the code, which is found in the file options.f90:
!============== options.f90 ==================
subroutine get_the_options
use global_data
use getopt_m !from getopt.f90
implicit none
call getarg(0,prog)
do
select case( getopt( "-hL:b:s:S:n:r:u" ))
case( ’L’ )
read(optarg,*)L
case( ’b’ )
read(optarg,*)beta
case( ’s’ )
read(optarg,*)start
case( ’S’ )
read(optarg,*)seed
case( ’n’ )
read(optarg,*)nsweep
case( ’r’ )
read(optarg,*)ranlux_level
case( ’u’ )
open (28, file="/dev/urandom", &
access="stream", form="unformatted")
read (28) seed
seed = ABS(seed)
close(28)
case( ’h’ )
call usage
case( ’?’ )
print *, ’unknown option ’, optopt
stop
case( char(0)) ! done with options
exit
case( ’-’ ) ! use -- to exit from options
exit
case default
print *, ’unhandled option ’, optopt
end select
enddo
end subroutine get_the_options
The command call getarg(0,prog) stores the name of the program in the
command line to the character variable prog. The function getopt is a
function written by Mark Gates and its code is in the file getopt.f90.
It is programmed so that its usage is similar to the corresponding C
function .
The argument "-hL:b:s:S:n:r:u" in getopt defines the allowed options ’-’,
’L’, ’b’, ’s’, ’S’, ’n’, ’r’, ’u’. When a user passes one of those through
the command line (e.g. -L 100, -h) the do loop takes us to the corresponding
CASE. If an option does not take an argument (e.g. -h), then a set of commands
can be executed, like call usage. If an option takes an argument, this is marked
by a semicolon in the argument of getopt (e.g. L:, b:, ...) and the argument can
be accessed through the character variable optarg. For example, the
statements
case( ’L’ )
read(optarg,*)L
and the command line arguments -L 10 set optarg to be equal to ’10’. Be
careful, ’10’ is not a number, but a string of characters! In order to convert the
character ’10’ to the integer 10 we use the command READ, where instead of a
unit number in its arguments we put the variable name. We do the same for the
other simulation parameters.
The subroutine locerr takes a character variable in its argument which prints
it to the stderr together with the name of the program in the command line.
Then it stops the execution of the program:
subroutine locerr(errmes)
use global_data
implicit none
character(*) :: errmes
write(0,’(A,A)’),TRIM(prog),’:’,TRIM(errmes),’ Exiting....’
stop 1
end subroutine locerr
Note the use of the intrinsic function TRIM which removes the trailing blanks of a
character variable. If we hadn’t been using it, the variable character(1024) ::
prog would have been printed in 1024 character spaces, something that it
wouldn’t have been very pretty...
The subroutine usage is ... used very often! It is a constant reminder of the
way that the program is used and helps users with weak long and/or short term
memory!
subroutine usage
use global_data
implicit none
print ’(3A)’,’Usage: ’,TRIM(prog),’ [options]’
print ’( A)’,’ -L: Lattice length (N=L*L)’
print ’( A)’,’ -b: beta’
print ’( A)’,’ -s: start (0 cold, 1 hot, 2 old config.)’
print ’( A)’,’ -S: seed’
print ’( A)’,’ -n: number of sweeps and measurements’
print ’( A)’,’ -u: seed from /dev/urandom’
print ’( A)’,’ -r: ranlux_level’
print ’( A)’,’Monte Carlo simulation of 2d Ising Model....’
stop
end subroutine usage
The subroutine simmessage is also quite important. It “labels” our results by
printing all the information that defines the simulation. It is very important to
label all of our data with this information, otherwise it can be dangerously useless!
Imagine a set of energy measurements without knowing the lattice size and/or the
temperature... Other useful information may turn out to be crucial, even though
we might not appreciate it at programming time: The name of the computer, the
operating system, the user name, the date etc. By varying the unit number in
the argument, we can print the same information in any file we want.
subroutine simmessage(unit)
use global_data
implicit none
integer :: unit
character(100) :: user,host,mach,tdate
call GETLOG(user)
call GETENV(’HOST’ ,host)
call GETENV(’HOSTTYPE’,mach)
call FDATE (tdate)
write(unit,’( A )’)&
’# #######################################################’
write(unit,’( A )’)&
’# 2d Ising Model, Metropolis algorithm on square lattice’
write(unit,’( 8A )’)&
’# Run on ’,TRIM(host),’ (’,TRIM(mach),’) by ’,TRIM(user),&
’ on ’,TRIM(tdate)
write(unit,’( A,I6,A )’)’# L = ’,L,’ (N=L*L)’
write(unit,’( A,I14 )’)’# seed = ’,seed
write(unit,’( A,I12,A )’)’# nsweeps = ’,nsweep,’ (No. sweeps)’
write(unit,’( A,G28.17)’)’# beta = ’,beta
write(unit,’( A,I4 ,A )’)’# start = ’,start,&
’ (0 cold, 1 hot, 2 old config)’
end subroutine simmessage
The compilation can be done with the command:
> gfortran global_data.f90 getopt.f90 \
main.f90 init.f90 met.f90 measure.f90 end.f90 \
options.f90 ranlux.F -o is
It is important to note that the files containing modules, like global_data.f90
and getopt.f90, must precede the files with the code that use the modules.
In order to run the program we pass the parameters through options in the
command line, like for example:
> /usr/bin/time ./is -L 10 -b 0.44 -s 1 -S 5342 -n 10000 \
>& out.dat &
The command time is added in order to measure the computer resources (CPU
time, memory, etc) that the program uses at run time.
A useful tool for complicated compilations is the utility make. Its
documentation is several hundred pages which can be accessed through the info
pages
and the interested reader is encouraged to browse through it.
If in the current directory there is a file named Makefile whose
contents
are
# #################### Makefile ############################
FC = gfortran
OBJS = global_data.o getopt.o ranlux.o \
main.o init.o met.o measure.o end.o options.o
FFLAGS = -O2
is: $(OBJS)
$(FC) $(FFLAGS) $^ -o $@
$(OBJS): global_data.f90
options.o: getopt.f90
%.o: %.f90
$(FC) $(FFLAGS) -c -o $@ $<
then this instructs the program make how to “make” the executable file is. What
have we gained? In order to see that, run make for the first time. Then try making
a trivial change in the file main.f90 and rerun make. Then only the modified file
is compiled and not the ones that have not been touched. This is accomplished by
defining dependencies in Makefile which execute commands conditionally
depending on the time stamps on the relevant files. Dependencies are defined in
lines which are of the form keyword: word1 word2 .... For example, the line
options.o: getopt.f90 defines a dependency of the file options.o from the
file getopt.f90. Lines 2-4 in the above Makefile define variables which
can be used in the commands that follow. There are many predefined
variables
in make which makes make programming easier. By using make in a large
project, we can automatically link to libraries, pass complicated compiler
options, do conditional compilation (depending, e.g., on the operating
system, the compiler used etc), etc. A serious programmer needs to invest
some time in order to use the full potential of make for the needs of her
project .
13.4 Thermalization
The problem of thermalization can be important for some systems studied with
Monte Carlo simulations. Even though it will not be so important in the
simulations performed in this book, we will discuss it because of its importance in
other problems. The reader should bear in mind that the thermalization problem
becomes more serious with increasing system size and when autocorrelation times
are large.
In a Monte Carlo simulation, the system is first put in a properly chosen initial
configuration in order to start the Markov process. In section 12.2 we saw that
when a system is in thermal equilibrium with a reservoir at a given temperature,
then a typical state has energy that differs very little from its average value
and belongs to a quite restricted region of phase space. Therefore, if we
choose an initial state that is far from this region, then the system has to
perform a random walk in the space of states until it finds the region
of typical states. This is the thermalization process in a Monte Carlo
simulation.
There are two problems that need to be addressed: The first one is the
appropriate choice of the initial configuration and the second one is to find criteria
that will determine when the system is thermalized. For the Ising model the initial
configuration is either, (a) cold, (b) hot or (c) old state. It is obvious that
choosing a hot state in order to simulate the system at a cool temperature is not
the best choice, and the system will take longer to thermalize than if we choose a
cold state or an old state at a nearby temperature. This is clearly seen in figure
13.7.
Thermalization depends on the temperature and the system size, but it also
depends on the physical quantity that we measure. Energy is thermalized faster
than magnetization. In general, a local quantity thermalizes fast and a non local
one slower. For the Ising model, thermalization is easier far from the critical
temperature, provided that we choose an initial configuration in the same
phase. It is easier to thermalize a small system rather than a large one.
The second problem is to determine when the system becomes thermalized and
discard all measurements before that. One way is to start simulations using
different initial states, or by keeping the same initial state and using a
different sequence of random numbers. When the times histories of the
monitored quantities converge, we are confident that the system has been
thermalized. Figure 13.7 shows that the thermalization time can vary quite a
lot.
A more systematic way is to compute an expectation value by removing an
increasing number of initial measurements. When the results converge within the
statistical error, then the physical quantity that we measure has thermalized.
This process is shown in figures 13.10 and 13.11 where we progressively drop
 and
and  initial measurements until the
expectation value of the magnetization stabilizes within the limits of its statistical
error.
initial measurements until the
expectation value of the magnetization stabilizes within the limits of its statistical
error.
13.5 Autocorrelations
In order to construct a set of independent measurements using a Markov process,
the states put in the sample should be statistically uncorrelated. But for a process
using the Metropolis algorithm this is not possible. The next state differs from the
previous one by at most one value of their spins. We would expect that we could
obtain an almost statistically independent configuration after one spin
update per site, a so called sweep of the lattice. This is indeed the case for
the Ising model for temperatures far from the critical region. But as one
approaches  , correlations between configurations obtained after a few
sweeps remain strong. It is easy to understand why this is happening.
As the correlation length
, correlations between configurations obtained after a few
sweeps remain strong. It is easy to understand why this is happening.
As the correlation length  (12.46) becomes much larger than a few
lattice spacings, large clusters of same spins are formed, as can be seen in
figure 13.32. For two statistically independent configurations, the size,
shape and position of those clusters should be quite different. For a single
flip algorithm, like the Metropolis algorithm, this process takes a lot of
time .
(12.46) becomes much larger than a few
lattice spacings, large clusters of same spins are formed, as can be seen in
figure 13.32. For two statistically independent configurations, the size,
shape and position of those clusters should be quite different. For a single
flip algorithm, like the Metropolis algorithm, this process takes a lot of
time .
For the quantitative study of autocorrelations between configurations we use
the autocorrelation function. Consider a physical quantity  (e.g. energy,
magnetization, etc) and let
(e.g. energy,
magnetization, etc) and let  be its value after Monte Carlo “time”
be its value after Monte Carlo “time”  .
.  can be measured in sweeps or multiples of it. The autocorrelation function
can be measured in sweeps or multiples of it. The autocorrelation function  of
of  is
is
 | (13.31) |
where  is the average value over the configurations in the sample for
is the average value over the configurations in the sample for
 . The normalization is such that
. The normalization is such that  .
.
The above definition reminds us the correlation function of spins in space (see
equation (12.45) ) and the discussion about its properties is similar to the one of
section 12.4. In a few words, when the value of  after time
after time  is strongly
correlated to the one at
is strongly
correlated to the one at  , then the product in the numerator in
(13.31) will be positive most of the time and the value of
, then the product in the numerator in
(13.31) will be positive most of the time and the value of  will be
positive. When the correlation is weak, the product will be positive and
negative the same number of times and
will be
positive. When the correlation is weak, the product will be positive and
negative the same number of times and  will be almost zero. In the
case of anti-correlations
will be almost zero. In the
case of anti-correlations  is negative. Negative values of
is negative. Negative values of  occur, but these are artifacts of the finite size of the sample and should be
rejected.
occur, but these are artifacts of the finite size of the sample and should be
rejected.
Asymptotically  drops exponentially
drops exponentially
 | (13.32) |
 is the time scale of decorrelation of the measurements of
is the time scale of decorrelation of the measurements of  and it is called the
autocorrelation time of
and it is called the
autocorrelation time of  . After time
. After time  ,
,  has dropped to the
has dropped to the  of its initial value and then we say that we have an independent measurement
of
of its initial value and then we say that we have an independent measurement
of
 . Therefore, if we have
. Therefore, if we have  measurements, the number of independent
measurements of
measurements, the number of independent
measurements of  is
is
 | (13.33) |
For expensive measurements we should measure every  sweeps. If the cost
of measurement is not significant, then we usually measure more often, since there
is still statistical information even in slightly correlated configurations. An
accurate determination of
sweeps. If the cost
of measurement is not significant, then we usually measure more often, since there
is still statistical information even in slightly correlated configurations. An
accurate determination of  is not easy since it requires measuring for
is not easy since it requires measuring for  .
.
An example is shown in figure 13.12 for the case of the magnetization
( ). We calculate the function
). We calculate the function  and we see that a fit to equation
(13.32) is quite good for
and we see that a fit to equation
(13.32) is quite good for  sweeps. The calculation is performed on a
sample of
sweeps. The calculation is performed on a
sample of  measurements with 1 measurement/sweep. Therefore the number
of independent measurements is
measurements with 1 measurement/sweep. Therefore the number
of independent measurements is  .
.
Another estimator of the autocorrelation time is the so called integrated
autocorrelation time  . Its definition stems from equation (13.32) where we
take
. Its definition stems from equation (13.32) where we
take
 | (13.34) |
The values of  and
and  differ slightly due to systematic errors that come from the
corrections
to equation (13.32) . The upper limit of the integral is cut off by a maximum
value
differ slightly due to systematic errors that come from the
corrections
to equation (13.32) . The upper limit of the integral is cut off by a maximum
value 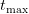
 | (13.35) |
For large enough  we observe a plateau in the plot of the value of
we observe a plateau in the plot of the value of
 which indicates convergence, and we take this as the estimator of
which indicates convergence, and we take this as the estimator of
 . For even larger
. For even larger  , finite sample effects enter in the sum that should be
discarded.
, finite sample effects enter in the sum that should be
discarded.
This calculation is shown in figure 13.14 where we used the same measurements
as the ones in figure 13.12. We find that  sweeps, which
is somewhat smaller than the autocorrelation time that we calculated
using the exponential fit to the autocorrelation function. If we are
interested in the scaling properties of the autocorrelation time with the
size of the system
sweeps, which
is somewhat smaller than the autocorrelation time that we calculated
using the exponential fit to the autocorrelation function. If we are
interested in the scaling properties of the autocorrelation time with the
size of the system  or the temperature
or the temperature  , then this difference is not
important .
The calculation of
, then this difference is not
important .
The calculation of  is quicker since it involves no
fitting .
is quicker since it involves no
fitting .
Autocorrelation times are not a serious problem away from the critical region.
Figures 13.15 and 13.16 show that they are no longer than a few sweeps and that
they are independent of the system size  . As we approach the critical region,
autocorrelation times increase. At the critical region we observe scaling of their
values with the system size, which means that for large
. As we approach the critical region,
autocorrelation times increase. At the critical region we observe scaling of their
values with the system size, which means that for large  we have that
we have that
 | (13.36) |
This is the phenomenon of critical slowing down. For the Metropolis
algorithm and the autocorrelation time of the magnetization, we have that
 [60]. This is a large value and that makes the algorithm
expensive for the study of the critical properties of the Ising model. It means that
the simulation time necessary for obtaining a given number of independent
configurations increases as
[60]. This is a large value and that makes the algorithm
expensive for the study of the critical properties of the Ising model. It means that
the simulation time necessary for obtaining a given number of independent
configurations increases as
 | (13.37) |
In the next chapter, we will discuss the scaling relation (13.36) in more detail
and present new algorithms that reduce critical slowing down drastically.
13.6 Statistical Errors
The estimate of the expectation value of an observable from its average value in a
sample gives no information about the quality of the measurement. The complete
information is provided by the full distribution, but in practice we are usually
content with the determination of the “statistical error” of the measurement. This
is defined using the assumption that the distribution of the measurements is
Gaussian, which is a very good approximation if the measurements are
independent. The statistical error is determined by the fluctuations of the values
of the observable in the sample around its average (see discussion in section 12.2
and in particular equation (12.27) ). Statistical errors can be made to
vanish, because they decrease as the inverse square root of the size of the
sample.
Besides statistical errors, one has systematic errors, which are harder to
control. Some of them are easier to control (like e.g. poor thermalization) and
others maybe hard even to realize their effect (like e.g. a subtle problem in a
random number generator). In the case of a discrete, finite, lattice, approximating
a continuous theory, there are systematic errors due to the discretization and the
finite size of the system. These errors are reduced by simulating larger systems
and by using several techniques (e.g. finite size scaling) in order to extrapolate the
results to the thermodynamic limit. These will be studied in detail in the
following chapter.
13.6.1 Errors of Independent Measurements
Using the assumption that the source of statistical errors are the thermal
fluctuations around the average value of an observable, we conclude that its
expectation value can be estimated by the mean of the sample and its error by the
error of the mean. Therefore if we have a sample of  measurements
measurements
 , their mean is an estimator of
, their mean is an estimator of 
 | (13.38) |
The error of the mean is an estimator of the statistical error 
 | (13.39) |
The above equations assume that the sample is a set of statistically
independent measurements. This is not true in a Monte Carlo simulation
due to the presence of autocorrelations. If the autocorrelation time,
measured in number of measurements, is  , then according to equation
13.33 we will have
, then according to equation
13.33 we will have  independent measurements. One can
show that in this case, the statistical error in the measurement of
independent measurements. One can
show that in this case, the statistical error in the measurement of  is
[61]
is
[61]
 | (13.40) |
If  , then we obtain equation (13.39) . If
, then we obtain equation (13.39) . If 
which is nothing but equation (13.39) for  independent measurements (we
assumed that
independent measurements (we
assumed that  ). The above relation is consistent with our
assumption that measurements become independent after time
). The above relation is consistent with our
assumption that measurements become independent after time  .
.
In some cases, the straightforward application of equations (13.41) is not
convenient. This happens when, measuring the autocorrelation time according to
the discussion in section 13.5, becomes laborious and time consuming. Moreover,
one has to compute the errors of observables that are functions of correlated
quantities, like in the case of the magnetic susceptibility (13.30) . The
calculation requires the knowledge of quantities that are not defined on
one spin configuration, like  and
and  (or
(or  on each
configuration
on each
configuration  ). After these are calculated on the sample, the error
). After these are calculated on the sample, the error  is not a simple function of
is not a simple function of  and
and  . This is because of the
correlation between the two quantities and the well known formula of
error propagation
. This is because of the
correlation between the two quantities and the well known formula of
error propagation  cannot be
applied.
cannot be
applied.
13.6.2 Jackknife
The simplest solution to the problems arising in the calculation of statistical
errors discussed in the previous section is to divide a sample into blocks or
bins. If one has  measurements, she can put them in
measurements, she can put them in  “bins” and
each bin is to be taken as an independent measurement. This will be
true if the number of measurements per bin
“bins” and
each bin is to be taken as an independent measurement. This will be
true if the number of measurements per bin  . If
. If 
 is average value of
is average value of  in the bin
in the bin  , then the error is given by
(13.39)
, then the error is given by
(13.39)
 | (13.42) |
This is the binning or blocking method and it is quite simple in its use. Note that
quantities, like the magnetic susceptibilities, are calculated in each bin as if
the bin were an independent sample. Then the error is easily calculated
by equation (13.42) . If the bin is too small and the samples are not
independent, then the error is underestimated by a factor of  (see
equation (13.40) ). The bins are statistically independent if
(see
equation (13.40) ). The bins are statistically independent if  . If
. If  is not a priori known we compute the error (13.42) by decreasing the
number of bins
is not a priori known we compute the error (13.42) by decreasing the
number of bins  . When the error is not increasing anymore and takes on
a constant value, then the calculation converges to the true statistical
error.
. When the error is not increasing anymore and takes on
a constant value, then the calculation converges to the true statistical
error.
But the method of choice in this book is the jackknife method. It is
more stable and more reliable, especially if the sample is small. The basic
idea is similar to the binning method. The difference is that the bins are
constructed in a different way and equation (13.42) is slightly modified.
The data is split in  bins which contain
bins which contain  elements as
follows: The bin
elements as
follows: The bin  contains the part of the sample obtained after we
we erase the contents of the
contains the part of the sample obtained after we
we erase the contents of the  -th bin of the binning method from the
full sample
-th bin of the binning method from the
full sample  . The procedure is depicted in figure 13.21.
. The procedure is depicted in figure 13.21.
We calculate the average value of  in each bin and we obtain
in each bin and we obtain
 . Then the statistical error in the measurement of
. Then the statistical error in the measurement of  is
is
 | (13.43) |
In order to determine the error, one has to vary the number of bins and check for
the convergence of (13.43) , like in the case of the binning method.
For more details and proofs of the above statements, the reader is referred to
the book of Berg [5]. Appendix 13.8.1 provides examples and a program for the
calculation of jackknife errors.
13.6.3 Bootstrap
Another useful method for the estimation of statistical errors is the bootstrap
method. Suppose that we have  independent measurements. From these we
create
independent measurements. From these we
create  random samples as follows: We choose one of the
random samples as follows: We choose one of the  measurements
with equal probability. We repeat
measurements
with equal probability. We repeat  times using the same set of
times using the same set of  measurements - i.e. by putting the chosen measurements back to the sample. This
means that on the average
measurements - i.e. by putting the chosen measurements back to the sample. This
means that on the average  of the sample will consist of the
same measurements. In each sample
of the sample will consist of the
same measurements. In each sample  we calculate the average
values
we calculate the average
values  and from those
and from those
 | (13.44) |
and
 | (13.45) |
The estimate for the error in  is
is
 | (13.46) |
We stress that the above formula gives the error for independent measurements.
If we have non negligible autocorrelation times, then we must use the
correction
 | (13.47) |
Appendix 13.8.2 discusses how to use the bootstrap method in order to calculate
the true error  without an a priori knowledge of
without an a priori knowledge of  . For more details, the
reader is referred to the articles of Bradley Efron [62]. In appendix 13.8.2
you will find examples and a program that implements the bootstrap
method.
. For more details, the
reader is referred to the articles of Bradley Efron [62]. In appendix 13.8.2
you will find examples and a program that implements the bootstrap
method.
13.7 Appendix: Autocorrelation Function
This appendix discusses the technical details of the calculation of the
autocorrelation function (13.31) and the autocorrelation time given by equations
(13.32) and (13.34) . The programs can be found in the directory Tools in the
accompanying software.
If we have a finite sample of  measurements
measurements  ,
then we can use the following estimator for the autocorrelation function, given by
equation (13.31) ,
,
then we can use the following estimator for the autocorrelation function, given by
equation (13.31) ,
 | (13.48) |
where the average values are computed from the
equations
 | (13.49) |
The constant  is chosen so that
is chosen so that  .
.
The program for the calculation of (13.48) and the autocorrelation time
(13.34) is listed below. It is in the file autoc.f90 and you should read the
comments embedded in the code for explanations of the most important
steps.
!======================================================
!file: autoc.f90
MODULE rho_function
implicit none
SAVE
integer :: NMAX,tmax
character(200) :: prog
CONTAINS
!------------------------------------------------------
!rho is the unnormalized autocorrelation function at t:
real(8) function rho(x,ndat,t)
implicit none
integer :: ndat,t
real(8),dimension(0:) :: x
integer :: n,t0
real(8) :: xav0,xavt,r
!--------------------------------------
n=ndat-t
if(n<1) call locerr(’rho: n<1’)
!Calculate the two averages: xav0=<x>_0, xavt=<x>_t
xav0 = SUM( x(0:n-1 )) / n
xavt = SUM( x(t:n-1+t)) / n
rho = SUM((x(0:n-1)-xav0)*(x(t:n-1+t)-xavt))/n
end function rho
!------------------------------------------------------
subroutine locerr(errmes)
implicit none
character(*) :: errmes
write(0,’(A,A)’),TRIM(prog),’:’,TRIM(errmes),’ Exiting....’
stop 1
end subroutine locerr
END MODULE rho_function
!======================================================
program autocorrelations
USE rho_function
implicit none
real(8),allocatable,dimension(:) :: r,tau,x
real(8) :: norm
integer :: i,ndat,t,tcut,chk
!------------------------------------------------------
!Default values for max number of data and max time for
!rho and tau:
NMAX=2000000;tmax=1000 !NMAX=2e6 requires ~ 2e6*8=16MB
call get_the_options
ALLOCATE(x(0:NMAX-1),STAT=chk)
if(chk > 0) call locerr(’Not enough memory for x’)
ndat=0
do while ( ndat < NMAX)
read(*,*,END=101)x(ndat)
ndat = ndat+1
enddo !
101 continue
if(ndat >= NMAX) write(0,’(3A,I14,A,I14)’) &
’# ’,TRIM(prog), &
’: Warning: read ndat=’, ndat, &
’ and reached the limit: ’,NMAX
!We decrease tmax if it is comparable or large of ndat
if(tmax > (ndat/10) ) tmax = ndat/10
!r(t) stores the values of the autocorrelation function rho(t)
ALLOCATE(r(0:tmax-1))
do t=0,tmax-1
r(t) = rho(x,ndat,t)
enddo
norm = 1.0D0/r(0); r = norm*r
!tau(t) stores integrated autocorrelation times with tcht=t
ALLOCATE(tau(0:tmax-1))
do tcut=0,tmax-1
tau(tcut)=0.0D0
do t=0,tcut
tau(tcut) = tau(tcut)+r(t)
enddo
enddo
!Output:
print ’(A)’,’# ===========================================’
print ’(A)’,’# Autoc function rho and int autoc time tau ’
print ’(A,I12,A,I8)’,’# ndat= ’,ndat,’ tmax= ’,tmax
print ’(A)’,’# t rho(t) tau(tcut=t) ’
print ’(A)’,’# ===========================================’
do t=0,tmax-1
print ’(I8,2G28.17)’,t,r(t),tau(t)
enddo
end program autocorrelations
!======================================================
subroutine get_the_options
use rho_function
use getopt_m !from getopt.f90
implicit none
call getarg(0,prog)
do
select case( getopt( "-ht:n:" ))
case( ’t’ )
read(optarg,*)tmax
case( ’n’ )
read(optarg,*)NMAX
case( ’h’ )
call usage
case( ’?’ )
print *, ’unknown option ’, optopt
stop
case( char(0)) ! done with options
exit
case( ’-’ ) ! use -- to exit from options
exit
case default
print *, ’unhandled option ’, optopt
end select
enddo
end subroutine get_the_options
!======================================================
subroutine usage
use rho_function
implicit none
print ’(3A)’,’Usage: ’,TRIM(prog),&
’ [-t <maxtime>] [-n <ndat>]’
print ’( A)’,’ Reads data from stdin (one column) and’
print ’( A)’,’ computes autocorrelation function and’
print ’( A)’,’ integrated autocorrelation time.’
stop
end subroutine usage
!======================================================
The calculation of the autocorrelation function is put in a separate module
rho_function which can be used by any of your programs. After the statement
CONTAINS we can add code for functions and subroutines which can be
accessed
by any program unit that uses the module. The module makes global variables,
like NMAX, tmax and prog, accessible to all program units that use the
module.
The compilation is done with the commands
> gfortran -O2 getopt.f90 autoc.f90 -o autoc
If our data is written in a file named data in one column, then the calculation of
the autocorrelation function and the autocorrelation time is done with the
command
> cat data | ./autoc > data.rho
The results are written to the file data.rho in three columns. The first one
is the time  , the second one is
, the second one is  and the third one is
and the third one is  (equation (13.35) ). The corresponding plots are constructed by the gnuplot
commands:
(equation (13.35) ). The corresponding plots are constructed by the gnuplot
commands:
gnuplot> plot "data.rho" using 1:2 with lines
gnuplot> plot "data.rho" using 1:3 with lines
If we wish to increase the maximum number of data NMAX or the maximum time
tmax, then we use the options -n and -t respectively:
> cat data | autoc -n 20000000 -t 20000 > data.rho
For doing all the work at once using gnuplot, we can give the command:
gnuplot> plot "<./is -L 20 -b 0.4407 -s 1 -S 345 -n 400000|\
grep -v ’#’|awk ’{print ($2>0)?$2:-$2;}’ |\
autoc -t 500" using 1:2 with lines
The above command is long and it is broken into 3 lines for better printing. You
can type it in one line by removing the trailing ∖.
A script that works out many calculations together is listed below. It is in the
file autoc_L and computes the data shown in figure 13.19.
#!/bin/tcsh -f
set nmeas = 2100000
set Ls = (5 10 20 40 60 80)
set beta = 0.4407
set tmax = 2000
foreach L ($Ls)
set N = ‘awk -v L=$L ’BEGIN{print L*L}’‘
set rand = ‘perl -e ’srand();print int(3000000*rand())+1;’‘
set out = outL${L}b${beta}
echo "Running L${L}b${beta}"
./is -L $L -b $beta -s 1 -S $rand -n $nmeas > $out
echo "Autocorrelations L${L}b${beta}"
grep -v ’#’ $out | \
awk -v N=$N ’NR>100000{print ($2>0)?($2/N):(-$2/N)}’|\
autoc -t $tmax > $out.rhom
end
Then we give the gnuplot commands:
gnuplot> plot "outL5b0.4407.rhom" u 1:2 w lines title "5"
gnuplot> replot "outL10b0.4407.rhom" u 1:2 w lines title "10"
gnuplot> replot "outL20b0.4407.rhom" u 1:2 w lines title "20"
gnuplot> replot "outL40b0.4407.rhom" u 1:2 w lines title "40"
gnuplot> replot "outL60b0.4407.rhom" u 1:2 w lines title "60"
gnuplot> replot "outL80b0.4407.rhom" u 1:2 w lines title "80"
The plots in figure 13.17 are constructed in a similar way.
For the calculation of  we do the following:
we do the following:
gnuplot> f(x) = c * exp(-x/t)
gnuplot> set log y
gnuplot> plot [:1000] "outL40b0.4407.rhom" u 1:2 with lines
gnuplot> c = 1 ; t = 300
gnuplot> fit [150:650] f(x) "outL40b0.4407.rhom" u 1:2 via c,t
gnuplot> plot [:1000] "outL40b0.4407.rhom" u 1:2 w lines,f(x)
gnuplot> plot [:] "outL40b0.4407.rhom" u 1:3 w lines
where in the last line we compute  . The fit command is just
an example and one should try different fitting ranges. The first plot
command shows graphically the approximate range of the exponential
falloff of the autocorrelation function. We should vary the upper and
lower limits of the fitting range until the value of
. The fit command is just
an example and one should try different fitting ranges. The first plot
command shows graphically the approximate range of the exponential
falloff of the autocorrelation function. We should vary the upper and
lower limits of the fitting range until the value of  stabilizes and
the
stabilizes and
the  is minimized .
The
is minimized .
The  of the fit can be read off from the output of the command
fit
of the fit can be read off from the output of the command
fit
.....
degrees of freedom (FIT_NDF) : 449
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.000939201
variance of residuals(reduced chisquare) = WSSR/ndf: 8.82099e-07
Final set of parameters Asymptotic Standard Error
======================= ==========================
c = 0.925371 +/- 0.0003773 (0.04078%)
t = 285.736 +/- 0.1141 (0.03995%)
.....
from the line “variance of residuals”. From the next
lines we read the values of the fitted parameters with their
errors
and we conclude that  . We stress that this is the statistical error
of the fit for the given fitting range. But usually the largest contributions to the error
come from systematic errors, which, in our case, are seen by varying the fitting
range .
By trying different fitting ranges and using the criterion that the minimum
. We stress that this is the statistical error
of the fit for the given fitting range. But usually the largest contributions to the error
come from systematic errors, which, in our case, are seen by varying the fitting
range .
By trying different fitting ranges and using the criterion that the minimum
 doubles its minimum value, we find that
doubles its minimum value, we find that  .
.
In our case the largest systematic error comes from neglecting the effect of
smaller autocorrelation times. These make non negligible contributions for small
 .
.
By fitting to
 | (13.50) |
we have taken into account only the largest autocorrelation time.
One should take into account also the smaller autocorrelation times. In this
case we expect that  . We find that the data for
the autocorrelation function fit perfectly to the function
. We find that the data for
the autocorrelation function fit perfectly to the function
 | (13.51) |
As we can see in figures 13.22 and 13.23, the small  fit is excellent and the
result for the dominant autocorrelation time is
fit is excellent and the
result for the dominant autocorrelation time is  . The
secondary autocorrelation times are
. The
secondary autocorrelation times are  ,
,  which are
considerably smaller that
which are
considerably smaller that  .
.
The commands for the analysis are listed below:
gnuplot> h(x) = a1*exp(-x/t1) + a2*exp(-x/t2) + a3*exp(-x/t3)
gnuplot> a1 = 1; t1 = 285; a2 = 0.04; t2 = 56; \
a3 = 0.03; t3 = 10
gnuplot> fit [1:600] h(x) "outL40b0.4407.rhom" \
using 1:2 via a1,t1,a2,t2,a3,t3
...
Final set of parameters Asymptotic Standard Error
======================= ==========================
a1 = 0.922111 +/- 0.001046 (0.1135%)
t1 = 286.325 +/- 0.2354 (0.08221%)
a2 = 0.0462523 +/- 0.001219 (2.635%)
t2 = 56.6783 +/- 2.824 (4.982%)
a3 = 0.0300761 +/- 0.001558 (5.18%)
t3 = 10.5227 +/- 0.8382 (7.965%)
gnuplot> plot [:150][0.5:] "outL40b0.4407.rhom" using 1:2 \
with lines notit,h(x) ,f(x)
gnuplot> plot [:1000][0.01:] "outL40b0.4407.rhom" using 1:2 \
with lines notit,h(x) ,f(x)
13.8 Appendix: Error Analysis
13.8.1 The Jackknife Method
In this section we present a program that calculates the errors using the jackknife
method discussed in section 13.6.2. Figure 13.21 shows the division of the data
into bins. For each bin we calculate the average value of the quantity  and then
we use equation (13.43) in order to calculate the error. The program is in the file
jack.f90 which you can find in the directory Tools in the accompanying
software. The program calculates
and then
we use equation (13.43) in order to calculate the error. The program is in the file
jack.f90 which you can find in the directory Tools in the accompanying
software. The program calculates  ,
,  ,
,  and
and
 .
.
!======================================================
!file: jack.f90
MODULE jack_function
implicit none
SAVE
integer :: JACK,MAXDAT
character(200) :: prog
CONTAINS
!------------------------------------------------------
!jackknife function:
subroutine jackknife(ndat,jack,x,&
avO,erO,avchi,erchi)
integer :: ndat,jack !local jack...
real(8),dimension(0:) :: x
real(8) :: avO,erO,avchi,erchi
integer :: i,j,binw,bin
real(8),allocatable :: O(:),chi(:)
!--------------------------------------
ALLOCATE(O(0:jack-1));ALLOCATE(chi(0:jack-1))
O=0.0D0;chi=0.0D0;
binw=ndat/jack
if(binw<1)call locerr(’jackknife: binw < 1’)
!Average value:
do i=0,ndat-1
do j=0,jack-1
if((i/binw) /= j) &
O (j) = O (j) + x(i)
enddo
enddo
O = O /(ndat-binw) !normalize
!Susceptibility:
do i=0,ndat-1
do j=0,jack-1
if((i/binw) /= j) &
chi(j) = chi(j) + (x(i)-O(j))*(x(i)-O(j))
enddo
enddo
chi = chi/(ndat-binw) !normalize
!---------------
avO = SUM(O)/jack;avchi=SUM(chi)/jack
erO = sqrt(SUM((O -avO )*(O -avO )))
erchi = sqrt(SUM((chi-avchi)*(chi-avchi)))
!---------------
DEALLOCATE(O);DEALLOCATE(chi)
end subroutine jackknife
!------------------------------------------------------
subroutine locerr(errmes)
implicit none
character(*) :: errmes
write(0,’(A,A)’),TRIM(prog),’:’,TRIM(errmes),’ Exiting....’
stop 1
end subroutine locerr
END MODULE jack_function
!======================================================
program jackknife_errors
use jack_function
implicit none
integer :: ndat,chk
real(8) :: O,dO,chi,dchi
real(8),allocatable :: x(:)
MAXDAT=1000000;JACK=10
call get_the_options
ALLOCATE(x(0:MAXDAT-1),STAT=chk)
if(chk > 0) call locerr(’Not enough memory for x’)
ndat=0
do while ( ndat < MAXDAT)
read(*,*,END=101)x(ndat)
ndat = ndat+1
enddo
101 continue
if(ndat >= MAXDAT) write(0,’(3A,I14,A,I14)’) &
’# ’,TRIM(prog), &
’: Warning: read ndat=’, ndat, &
’ and reached the limit: ’,MAXDAT
call jackknife(ndat,JACK,x,O,dO,chi,dchi)
print ’(A,I14,A,I12,A)’,’# NDAT = ’,ndat, &
’ data. JACK = ’,JACK,’ groups’
print ’(A)’,’# <o>, chi= (<o^2>-<o>^2)’
print ’(A)’,’# <o> +/- err chi +/- err’
print ’(4G28.17)’,O,dO,chi,dchi
end program jackknife_errors
!======================================================
subroutine get_the_options
use jack_function
use getopt_m !from getopt.f90
implicit none
call getarg(0,prog)
do
select case( getopt( "-hj:d:" ))
case( ’j’ )
read(optarg,*)JACK
case( ’d’ )
read(optarg,*)MAXDAT
case( ’h’ )
call usage
case( ’?’ )
print *, ’unknown option ’, optopt
stop
case( char(0)) ! done with options
exit
case( ’-’ ) ! use -- to exit from options
exit
case default
print *, ’unhandled option ’, optopt
end select
enddo
end subroutine get_the_options
!=============================================
subroutine usage
use jack_function
implicit none
print ’(3A)’,’Usage: ’,TRIM(prog),’ [options]’
print ’( A)’,’ -j : No. jack groups Def. 10’
print ’( A)’,’ -d : Max. no. of data points read’
print ’( A)’,’Computes <o>, chi= (<o^2>-<o>^2)’
print ’( A)’,’Data is in one column from stdin.’
stop
end subroutine usage
For the compilation we use the command
> gfortran -O2 getopt.f90 jack.f90 -o jack
If we assume that our data is in one column in the file data, the command that
calculates the jackknife errors using 50 bins is:
> cat data | jack -j 50
The program has set a maximum of MAXDAT=1,000,000 measurements. If we need
to analyze more data, we have to use the switch -d. For example, for 2,000,000
measurements, use -d 2000000. The program reads data from the stdin and we
can construct filters in order to do complicated analysis tasks. For example, the
analysis of the magnetization produced by the output of the Ising model program
can be done with the command:
> ./is -L 20 -b 0.4407 -s 1 -S 342 -n 2000000 | grep -v # | \
awk -v L=20 ’{print ($2>0)?($2/(L*L)):(-$2/(L*L))}’ | \
./jack -j 50 -d 2000000 | grep -v # | \
awk -v b=0.4407 -v L=20 ’{print $1,$2,b*L*L*$3,b*L*L*$4}’
The command shown above can be written in one line by removing the
backslashes (’∖’) at the end of each line. Let’s explain it in detail: The first line
runs the program is for the Ising model with  lattice sites
(-L 20) and
lattice sites
(-L 20) and  (-b 0.4407). It starts the simulation from a hot
configuration (-s 1) and makes 2,000,000 measurements (-n 2000000). The
command grep -v filters out the comments from the output of the program,
which are lines starting with a #. The second line calls awk and defines the awk
variable L to be equal to 20 (-v L=20). For each line in its input, it prints the
absolute value of the second column ($2) divided by the number of lattice sites
L*L. The third line makes the jackknife calculation of the average values of
(-b 0.4407). It starts the simulation from a hot
configuration (-s 1) and makes 2,000,000 measurements (-n 2000000). The
command grep -v filters out the comments from the output of the program,
which are lines starting with a #. The second line calls awk and defines the awk
variable L to be equal to 20 (-v L=20). For each line in its input, it prints the
absolute value of the second column ($2) divided by the number of lattice sites
L*L. The third line makes the jackknife calculation of the average values of  and
and  with their errors using the program jack. The comments of
the output of the command jack are removed with the command grep -v. The
fourth line is needed only for the calculation of the magnetic susceptibility,
using equation (13.30) . There, we need to multiply the fluctuations
with their errors using the program jack. The comments of
the output of the command jack are removed with the command grep -v. The
fourth line is needed only for the calculation of the magnetic susceptibility,
using equation (13.30) . There, we need to multiply the fluctuations
 and their error by the factor
and their error by the factor  in order to obtain
in order to obtain
 .
.
13.8.2 The Bootstrap Method
In this subsection we present a program for the calculation of the errors using the
bootstrap method according to the discussion in section 13.6.3. The program is in
the file boot.f90:
!======================================================
!file: boot.f90
MODULE boot_function
implicit none
SAVE
integer :: SAMPLES,MAXDAT
character(200) :: prog
integer :: seed
CONTAINS
!------------------------------------------------------
!jackknife function:
subroutine bootstrap(ndat,samples,x,&
avO,erO,avchi,erchi)
integer :: ndat,samples !local samples...
real(8),dimension(0:) :: x
real(8) :: avO,erO,avchi,erchi
integer :: i,j,k
real(8),allocatable :: O(:),O2(:),chi(:)
!--------------------------------------
ALLOCATE(O(0:samples-1));ALLOCATE(O2(0:samples-1));
ALLOCATE(chi(0:samples-1))
O=0.0D0;O2=0.0D0;chi=0.0D0;
do j=0,samples-1
do i=0,ndat -1
k = INT(ndat*drandom()) !0,...,ndat-1
O (j) = O (j) + x(k)
O2(j) = O2(j) + x(k)*x(k)
enddo
O (j) = O(j)/ndat; O2(j) = O2(j)/ndat
chi(j) = O2(j)-O(j)*O(j)
enddo
!---------------
avO = SUM(O)/samples;avchi=SUM(chi)/samples
erO = sqrt(SUM((O -avO )*(O -avO ))/samples)
erchi = sqrt(SUM((chi-avchi)*(chi-avchi))/samples)
!compute the real avO:
avO = SUM(x(0:ndat-1))/ndat
!---------------
DEALLOCATE(O);DEALLOCATE(chi)
end subroutine bootstrap
!------------------------------------------------------
real(8) function drandom()
implicit none
integer,parameter :: a = 16807
integer,parameter :: m = 2147483647
integer,parameter :: q = 127773
integer,parameter :: r = 2836
real(8),parameter :: f = (1.0D0/m)
integer :: p
real(8) :: dr
101 continue
p = seed/q
seed = a*(seed- q*p) - r*p
if(seed .lt. 0) seed = seed + m
dr = f*seed
if( dr .le. 0.0D0 .or. dr .ge. 1.0D0) goto 101
drandom = dr
end function drandom
!------------------------------------------------------
subroutine locerr(errmes)
implicit none
character(*) :: errmes
write(0,’(A,A)’),TRIM(prog),’:’,TRIM(errmes),’ Exiting....’
stop 1
end subroutine locerr
END MODULE boot_function
!======================================================
program bootstrap_errors
use boot_function
implicit none
integer :: ndat,chk
real(8) :: O,dO,chi,dchi
real(8),allocatable :: x(:)
MAXDAT=1000000;SAMPLES=1000
call get_the_options
ALLOCATE(x(0:MAXDAT-1),STAT=chk)
if(chk > 0) call locerr(’Not enough memory for x’)
ndat=0
do while ( ndat < MAXDAT)
read(*,*,END=101)x(ndat)
ndat = ndat+1
enddo
101 continue
if(ndat >= MAXDAT) write(0,’(3A,I14,A,I14)’) &
’# ’,TRIM(prog), &
’: Warning: read ndat=’, ndat, &
’ and reached the limit: ’,MAXDAT
open (28, file="/dev/urandom", access="stream",&
form="unformatted")
read (28) seed
seed = ABS(seed)
close(28)
call bootstrap(ndat,SAMPLES,x,O,dO,chi,dchi)
print ’(A,I14,A,I12,A)’,&
’# NDAT = ’,ndat,’ data. SAMPLES = ’,SAMPLES,’ groups’
print ’(A )’,&
’# <o>, chi= (<o^2>-<o>^2)’
print ’(A )’,&
’# <o> +/- err chi +/- err’
print ’(4G28.17)’,O,dO,chi,dchi
end program bootstrap_errors
!======================================================
subroutine get_the_options
use boot_function
use getopt_m !from getopt.f90
implicit none
call getarg(0,prog)
do
select case( getopt( "-hs:d:" ))
case( ’s’ )
read(optarg,*)SAMPLES
case( ’d’ )
read(optarg,*)MAXDAT
case( ’h’ )
call usage
case( ’?’ )
print *, ’unknown option ’, optopt
stop
case( char(0)) ! done with options
exit
case( ’-’ ) ! use -- to exit from options
exit
case default
print *, ’unhandled option ’, optopt
end select
enddo
end subroutine get_the_options
!=============================================
subroutine usage
...
end subroutine usage
!=============================================
For the compilation we use the command
> gfortran -O2 getopt.f90 boot.f90 -o boot
If our data is in one column in the file data, then the command that calculates
the errors using 500 samples is:
> cat data | boot -s 500
The maximum number of measurements is set to 1,000,000 as in the jack
program. For more measurements we should use the -d switch, e.g. for 2,000,000
measurements use -d 2000000. For the analysis of the magnetization from the
output of the program is we can use the following command:
> is -L 20 -b 0.4407 -s 1 -S 342 -n 2000000 | grep -v # | \
awk -v L=20 ’{print ($2>0)?($2/(L*L)):(-$2/(L*L))}’ | \
boot -s 1000 -d 2000000 | grep -v # | \
awk -v b=0.4407 -v L=20 ’{print $1,$2,b*L*L*$3,b*L*L*$4}’
13.8.3 Comparing the Methods
In this subsection we will compute errors using equation (13.40) , the jackknife
method (13.43) and the bootstrap method (13.47) . In order to appreciate the
differences, we will use data with large autocorrelation times. We use the
Metropolis algorithm on the Ising model with  ,
,  and
measure the magnetization per site (13.28) . We take
and
measure the magnetization per site (13.28) . We take  measurements
using the commands:
measurements
using the commands:
> ./is -L 40 -b 0.4407 -s 1 -S 5434365 -n 1000000 \
> outL40b0.4407.dat &
> grep -v # outL40b0.4407.dat | \
awk -v L=40 ’{if($2<0){$2=-$2};print $2/(L*L)}’ \
> outL40b0.4407.m
> cat outL40b0.4407.m | autoc -t 10000 -n 1000000 \
> outL40b0.4407.rhom
The file outL40b0.4407.m has the measurements of the magnetization in one
column and the file outL40b0.4407.rhom has the autocorrelation function
and the integrated autocorrelation time as described after page 1429. We
obtain  . The integrated autocorrelation time is found to be
. The integrated autocorrelation time is found to be
 .
.
The expectation value is  . The application of equation
(13.39) , valid for independent measurements, gives the (underestimated) error
. The application of equation
(13.39) , valid for independent measurements, gives the (underestimated) error
 . Using equation (13.40) we obtain
. Using equation (13.40) we obtain  .
The error of the magnetic susceptibility cannot be calculated this way.
.
The error of the magnetic susceptibility cannot be calculated this way.
 | (13.52) |
For the calculation of the error of the magnetic susceptibility we have to resort
to the jackknife or to the bootstrap method. The latter is applied initially using a
variable number of samples 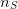 so that the optimal number of samples is
be determined. Figure 13.24 shows the results for the magnetization.
We observe a very fast convergence to
so that the optimal number of samples is
be determined. Figure 13.24 shows the results for the magnetization.
We observe a very fast convergence to 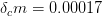 for quite small
number of samples. The analysis could have safely used
for quite small
number of samples. The analysis could have safely used  . In the
case of the magnetic susceptibility, convergence is slower, but we can
still use
. In the
case of the magnetic susceptibility, convergence is slower, but we can
still use 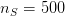 . We obtain
. We obtain  and
and  . The error
assumes independent measurements, something that is not true in our case.
We should use the correction factor
. The error
assumes independent measurements, something that is not true in our case.
We should use the correction factor  which gives
which gives  .
Therefore
.
Therefore
 | (13.53) |
We note that the error is quite large, which is because we have few independent
measurements:  . The a priori knowledge
of
. The a priori knowledge
of  is necessary in this calculation.
is necessary in this calculation.
In the case of the jackknife method, the calculation can proceed without an
priori knowledge of  . The errors are calculated for a variable number of bins
. The errors are calculated for a variable number of bins
 . Figure 13.26 shows the results for the magnetization. When
. Figure 13.26 shows the results for the magnetization. When  the
samples consist of all the measurements except one. Then the error is equal to the
error calculated using the standard deviation formula and it is underestimated by
the factor
the
samples consist of all the measurements except one. Then the error is equal to the
error calculated using the standard deviation formula and it is underestimated by
the factor  . This is shown in figure 13.26, where we observe a slow
convergence to the value
. This is shown in figure 13.26, where we observe a slow
convergence to the value  . The effect of the autocorrelations
vanishes when we delete
. The effect of the autocorrelations
vanishes when we delete  measurements from each bin. This
happens when
measurements from each bin. This
happens when  . Of
course this an order of magnitude estimate and a careful study is necessary in
order to determine the correct value for
. Of
course this an order of magnitude estimate and a careful study is necessary in
order to determine the correct value for  . Figure 13.26 shows that the error
converges for
. Figure 13.26 shows that the error
converges for  to the value
to the value  , which is quite close to
the value
, which is quite close to
the value  . We note that, by using a small number
. We note that, by using a small number
 , we obtain an acceptable estimate, a rule of the thumb that can be
used for quick calculations.
, we obtain an acceptable estimate, a rule of the thumb that can be
used for quick calculations.
Similar results are obtained for the magnetic susceptibility  , where the
error converges to the value
, where the
error converges to the value  , in accordance with the previous
estimates. For
, in accordance with the previous
estimates. For  the error converges to the underestimated error
the error converges to the underestimated error
 .
.
We can use the bootstrap method, in a similar way to the jackknife method, in
order to determine the real error  ,
,  without calculating
without calculating  directly. The
data is split into
directly. The
data is split into  bins, whose bin width is
bins, whose bin width is  . Each
jackknife bin contains
. Each
jackknife bin contains  data elements and we apply the bootstrap
method on this data, by taking
data elements and we apply the bootstrap
method on this data, by taking  samples of
samples of  random data. Then
each jackknife bin gives a measurement on which we apply equation (13.43) in
order to calculate errors.
random data. Then
each jackknife bin gives a measurement on which we apply equation (13.43) in
order to calculate errors.
The above calculations can be reversed and used for the calculation of the
autocorrelation time. By computing the underestimated error  and the true
error
and the true
error  using one of the methods described above, we can calculate
using one of the methods described above, we can calculate  using
the relation
using
the relation  . Therefore
. Therefore
 | (13.54) |
By calculating  using all the methods described here, these relations can also
be used in order to check the analysis for self-consistency and see if they agree.
This is not always a trivial work since a system may have many autocorrelation
times which influence each observable in a different way (fast modes, slow
modes).
using all the methods described here, these relations can also
be used in order to check the analysis for self-consistency and see if they agree.
This is not always a trivial work since a system may have many autocorrelation
times which influence each observable in a different way (fast modes, slow
modes).
13.9 Problems
- Prove that equation (13.22) satisfies the detailed balance condition.
- Write a program that prints the memory used by variables of the
type character, integer, integer(8), real, real(8) in bytes.
Calculate the amount of memory needed for an array of size 2,000,000
for each of the above types of variables.
- Make the appropriate changes in the Ising model program so that it
measures the average acceptance ratio
 of the Metropolis steps. I.e.
compute the ratio of accepted spin flips to the number of attempted
spin flips. Compute the dependence of
of the Metropolis steps. I.e.
compute the ratio of accepted spin flips to the number of attempted
spin flips. Compute the dependence of  on the temperature and
the size of the system. Take
on the temperature and
the size of the system. Take  and
and 






 . Then take
. Then take  ,
, 



 . Repeat for the same values of
. Repeat for the same values of  for
for  and
and
 .
.
- Reproduce the plots in figure 13.12 and compute
 . Repeat for
. Repeat for  .
Compare your results with
.
Compare your results with  and
and  .
.
- Reproduce the plots in figure 13.15 and repeat your calculation for the
energy.
- Reproduce the plots in figure 13.17. Repeat your calculation for the
energy. Then, construct similar plots for
 and
and  as a function
of
as a function
of  (see figure 13.14).
(see figure 13.14).
- Reproduce the plots in figures 13.19 and 13.20. Repeat your calculation
for the energy. Then, construct similar plots for
 and
and  as a
function of
as a
function of  (see figure 13.14).
(see figure 13.14).
- Modify the Ising model program presented in the text so that it
can simulate the Ising model in the presence of an external magnetic
field
 (see equation (13.2) ). Calculate the magnetization per site
(see equation (13.2) ). Calculate the magnetization per site
 for
for  and
and  at an interesting
range of temperatures. Use different initial configuration in order to
study the thermalization of the system as
at an interesting
range of temperatures. Use different initial configuration in order to
study the thermalization of the system as  increases: Cold state with
spins parallel to
increases: Cold state with
spins parallel to  , cold state with spins antiparallel to
, cold state with spins antiparallel to  and hot
state. Study the dependence of the critical temperature separating the
ordered from the disordered state on the value of
and hot
state. Study the dependence of the critical temperature separating the
ordered from the disordered state on the value of  .
.
- Hysteresis: In the previous problem, the Ising model with
 has a
first order phase transition, i.e. a discontinuity in the value of the order
parameter which in our case is the magnetization as a function of
has a
first order phase transition, i.e. a discontinuity in the value of the order
parameter which in our case is the magnetization as a function of  . Near
a first order transition we observe the phenomenon of hysteresis. In order to
see it, set
. Near
a first order transition we observe the phenomenon of hysteresis. In order to
see it, set  and
and  and
and
- thermalize the system for

- simulate the system for
 using as an initial state the last
one coming from the previous step. Do 100 sweeps and calculate
using as an initial state the last
one coming from the previous step. Do 100 sweeps and calculate
 .
.
- continue by increasing each time the magnetic field by
 .
Stop when
.
Stop when  .
.
- using the last configuration from the previous step, repeat by
decreasing the magnetic field by
 until
until  .
.
- using the last configuration from the previous step, repeat by
increasing the magnetic field by
 until
until  .
.
Make the plot  . What do you observe?
. What do you observe?
For systems near a first order phase transition, the order parameter can
take two different values with almost equal probability. This means
that the free energy has two local minima. Only one of them is the
true, global minimum. This is depicted in figure 12.2 where two
equally probable values of the order parameter are shown. This
happens exactly at the critical point. When we move away from the
critical point, one of the peaks grows and it is favored corresponding
to the global minimum of the free energy. The local minimum is
called a metastable state and when the system is in such a state, it
takes a long time until a thermal fluctuation makes it overcome the
free energy barrier and find the global minimum. In a Monte Carlo
simulation such a case presents a great difficulty in sampling states
correctly near the two local minima. Repeat the above simulations, this
time making  sweeps per point. Plot the time series of
the magnetization and observe the transitions from the metastable
state to the stable one and backwards. Compute the histogram of
the values of the magnetization and determine which state is the
metastable in each case. How is the histogram changing as
sweeps per point. Plot the time series of
the magnetization and observe the transitions from the metastable
state to the stable one and backwards. Compute the histogram of
the values of the magnetization and determine which state is the
metastable in each case. How is the histogram changing as  is
increased?
is
increased?
- Write a program that simulates the 2 dimensional Ising model on a
triangular lattice using the Metropolis algorithm. The main difference is
that the number of nearest neighbors is
 instead of
instead of  . Look into
chapter 13.1.2 of Newman and Barkema (esp. figure 13.4). Compute the
change in energy for each spin flip for the Metropolis step. Calculate the
maxima of the magnetic susceptibility and of the specific heat and see if
they are close to the expected critical temperature
. Look into
chapter 13.1.2 of Newman and Barkema (esp. figure 13.4). Compute the
change in energy for each spin flip for the Metropolis step. Calculate the
maxima of the magnetic susceptibility and of the specific heat and see if
they are close to the expected critical temperature  .
Note that even though
.
Note that even though  is different than the corresponding value
on the square lattice, the critical exponents are the same due to
universality.
is different than the corresponding value
on the square lattice, the critical exponents are the same due to
universality.
- Write a program that simulates the three dimensional Ising model on a
cubic lattice using the Metropolis algorithm. Use helical boundary
conditions (all you need in this case is to add a parameter ZNN=L*L together
with the XNN=1 and YNN=L).
- Write a program that simulates the three dimensional Ising model on a
cubic lattice using the Metropolis algorithm. Use periodic boundary
conditions. (Hint: Use a one dimensional array s(N). During initialization,
compute the arrays XNN(-N:N), YNN(-N:N), ZNN(-N:N) which store the
nearest neighbors of the position i on the lattice in XNN(i), XNN(-i),
YNN(i), YNN(-i), ZNN(i), ZNN(-i).)
- Simulate the antiferromagnetic two dimensional Ising model on a square
lattice using the Metropolis algorithm. You may use the same code that you
have and enter negative temperatures. Find the ground state(s) of the
system.
Define the staggered magnetization  to be the magnetization per site of
the sublattice consisting of sites with odd
to be the magnetization per site of
the sublattice consisting of sites with odd  and
and  coordinate. Set
coordinate. Set
 and compute the energy, the
and compute the energy, the  , the specific heat, the
magnetic susceptibility
, the specific heat, the
magnetic susceptibility  and the staggered magnetic susceptibility
and the staggered magnetic susceptibility
 .
.
 has a maximum in the region
has a maximum in the region  . Compute its value at this
temperature for
. Compute its value at this
temperature for  . Show that
. Show that  does not diverge as
does not diverge as  ,
therefore
,
therefore  does not show a phase transition.
does not show a phase transition.
Repeat the calculation for  . What do you conclude? Compare the
behavior of
. What do you conclude? Compare the
behavior of  for the antiferromagnetic Ising model with
for the antiferromagnetic Ising model with  of the
ferromagnetic.
of the
ferromagnetic.
- Modify the program in boot.f90 so that it bins its input data. Reproduce
the plots in figures ?? and ??. (Hint: See the file boot_bin.f90)
Chapter 14
Critical Exponents
In the previous chapters, we saw that when a system
undergoes a continuous phase transition as  , or equivalently as the reduced
temperature
, or equivalently as the reduced
temperature
 | (14.1) |
the correlation length 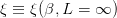 , calculated in the thermodynamic limit
diverges according to the relation
, calculated in the thermodynamic limit
diverges according to the relation
 | (14.2) |
The behavior of such systems near the phase transition is characterized by
critical exponents, such as the exponent  , which are the same for all
systems in the same universality class. The critical exponents describe the
leading non analytic behavior of the observables in the thermodynamic
limit
, which are the same for all
systems in the same universality class. The critical exponents describe the
leading non analytic behavior of the observables in the thermodynamic
limit
 , when
, when  . Systems with the same long distance behavior, but which
could possibly differ microscopically, belong to the same universality class. For
example, if we add a next to nearest neighbor interaction in the Hamiltonian
of the Ising model or if we consider the system on a triangular instead
of a square lattice, the system will still belong to the same universality
class. As
. Systems with the same long distance behavior, but which
could possibly differ microscopically, belong to the same universality class. For
example, if we add a next to nearest neighbor interaction in the Hamiltonian
of the Ising model or if we consider the system on a triangular instead
of a square lattice, the system will still belong to the same universality
class. As  these details become irrelevant and all these systems
have the same long distance behavior. Microscopic degrees of freedom of
systems in the same universality class can be quite different, as is the
case of the liquid/vapor phase transition at the triple point and the Ising
model.
these details become irrelevant and all these systems
have the same long distance behavior. Microscopic degrees of freedom of
systems in the same universality class can be quite different, as is the
case of the liquid/vapor phase transition at the triple point and the Ising
model.
The critical exponents of the 2d Ising model universality class are the Onsager
exponents:
 | (14.3) |
 | (14.4) |
 | (14.5) |
This behavior is seen only in the thermodynamic limit  . For a finite
lattice, all observables are analytic since they are calculated from the
analytic
partition function
. For a finite
lattice, all observables are analytic since they are calculated from the
analytic
partition function  given by equation (13.4) . When
given by equation (13.4) . When  the
model behaves approximately as the infinite system. As
the
model behaves approximately as the infinite system. As  and
and  finite size effects dominate. Then the fluctuations, e.g.
finite size effects dominate. Then the fluctuations, e.g.  and
and  , on the finite
lattice have a maximum for a pseudocritical temperature
, on the finite
lattice have a maximum for a pseudocritical temperature  for which we have
that
for which we have
that
 | (14.6) |
For the Ising model on the square lattice, defined by (13.14) , we have that
 .
.
Because of (14.2) , when on the finite lattice we take  , we have
that
, we have
that 

 , therefore equations
(14.3) – (14.5) become
, therefore equations
(14.3) – (14.5) become
 | (14.7) |
 | (14.8) |
 | (14.9) |
The left hand sides of the above relations are normally evaluated at  , but
they can also be evaluated at any temperature in the pseudocritical region. Most of
the times, one calculates the observables for
, but
they can also be evaluated at any temperature in the pseudocritical region. Most of
the times, one calculates the observables for  , but one can also use e.g.
, but one can also use e.g.
 .
In the next sections we will show how to calculate the critical exponents by using
the scaling relations (14.3) – (14.5) and (14.7) – (14.9) .
.
In the next sections we will show how to calculate the critical exponents by using
the scaling relations (14.3) – (14.5) and (14.7) – (14.9) .
14.1 Critical Slowing Down
The computation of critical exponents is quite involved and requires accurate
measurements, as well as simulations of large systems in order to reduce finite size
effects. The Metropolis algorithm suffers from severe critical slowing down, i.e.
diverging autocorrelation times with large dynamic exponent  according
to (13.36) , near the critical region, which makes it impossible to study
large systems. In this section we will discuss the cause of this effect whose
understanding will lead us to new algorithms that beat critical slowing down.
These are the cluster algorithms and, in particular, the Wolff algorithm. The
success of these algorithms is based on the dynamics of the system and, therefore,
they have a more specialized range of applications. In contrast, the Metropolis
algorithm can, in principle, be applied on any system studied with the Monte
Carlo method.
according
to (13.36) , near the critical region, which makes it impossible to study
large systems. In this section we will discuss the cause of this effect whose
understanding will lead us to new algorithms that beat critical slowing down.
These are the cluster algorithms and, in particular, the Wolff algorithm. The
success of these algorithms is based on the dynamics of the system and, therefore,
they have a more specialized range of applications. In contrast, the Metropolis
algorithm can, in principle, be applied on any system studied with the Monte
Carlo method.
According to the discussion in section 13.5, the Ising model simulation using
the Metropolis algorithm near the critical region exhibits an increase in
autocorrelation times given by the scaling relation (13.36)
 | (14.10) |
The correlation length of the finite system becomes  in this region, and we
obtain equation (13.36) ,
in this region, and we
obtain equation (13.36) ,  . When
. When  we have the effect of critical
slowing down.
we have the effect of critical
slowing down.
Critical slowing down is the main reason that prohibits the
simulation of very large systems, at least as far as CPU time  is
concerned .
The generation of a given number of configuration requires an effort
is
concerned .
The generation of a given number of configuration requires an effort  .
But the measurement of a local quantity, like
.
But the measurement of a local quantity, like  , for a given number
of times requires no extra cost, since each configuration yields
, for a given number
of times requires no extra cost, since each configuration yields  measurements .
In this case, measuring for the largest possible
measurements .
In this case, measuring for the largest possible  is preferable, since it reduces
finite size effects. We see that, in the absence of critical slowing down, the cost of
measurement of
is preferable, since it reduces
finite size effects. We see that, in the absence of critical slowing down, the cost of
measurement of  is
is  .
.
Critical slowing down, however, adds to the cost of production of independent
configurations and we obtain  , making the large
, making the large  simulations
prohibitively expensive. For the Metropolis algorithm on the two dimensional
Ising model we have that
simulations
prohibitively expensive. For the Metropolis algorithm on the two dimensional
Ising model we have that  ; and the problem is severe. Therefore, it is
important to invent new algorithms that beat critical slowing down. In the case of
the Ising model and similar spin systems, the solution is relatively easy. It is
special to the specific dynamics of spin systems and does not have a universal
application.
; and the problem is severe. Therefore, it is
important to invent new algorithms that beat critical slowing down. In the case of
the Ising model and similar spin systems, the solution is relatively easy. It is
special to the specific dynamics of spin systems and does not have a universal
application.
The reason for the appearance of critical slowing down is the divergence of the
correlation length  . As we approach the critical temperature
. As we approach the critical temperature  from the
disordered phase, the typical configurations are dominated by large clusters of
same spins. The Metropolis algorithm makes at most one spin flip per step and
the acceptance ratios for spins inside a cluster are small. For example, a spin with
four same neighboring spins can flip with probability
from the
disordered phase, the typical configurations are dominated by large clusters of
same spins. The Metropolis algorithm makes at most one spin flip per step and
the acceptance ratios for spins inside a cluster are small. For example, a spin with
four same neighboring spins can flip with probability 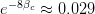 ,
which is quite small. The spins that change more often are the ones with
more neighbors having opposite spins, therefore the largest activity is
observed at the boundaries of the large clusters. In order to obtain a
statistically independent configuration, we need to destroy and create
many clusters, something that happens very slowly using the Metropolis
algorithm who realizes this process mostly by moving the boundaries of the
clusters.
,
which is quite small. The spins that change more often are the ones with
more neighbors having opposite spins, therefore the largest activity is
observed at the boundaries of the large clusters. In order to obtain a
statistically independent configuration, we need to destroy and create
many clusters, something that happens very slowly using the Metropolis
algorithm who realizes this process mostly by moving the boundaries of the
clusters.
14.2 Wolff Cluster Algorithm
Beating critical slowing down requires new algorithms so that at
each step a spin configuration is changed at the scale of a spin
cluster .
The cluster algorithms construct such regions of same spins in a way that the
proposed new configuration has all the spins of the clusters flipped. For such an
algorithm to be successful, the acceptance ratios should be large. The most
famous ones are the Swendsen-Wang [63] and the Wolff [64] cluster algorithms.
The process of constructing the clusters is stochastic and depends on the
temperature. Small clusters should be favored for  , whereas large clusters
of size
, whereas large clusters
of size  should dominate for
should dominate for  .
.
The basic idea of the Wolff algorithm is to choose a site randomly, a so called
seed of the cluster, and construct a spin cluster around it. At each step, we add
new members to the cluster with probability  . If
. If  is
properly chosen, the detailed balance condition (12.59) is satisfied and the new
configuration is always accepted. This process is depicted in figure 14.1. In the
state
is
properly chosen, the detailed balance condition (12.59) is satisfied and the new
configuration is always accepted. This process is depicted in figure 14.1. In the
state  , the cluster is enclosed by the dashed line. The new state
, the cluster is enclosed by the dashed line. The new state  is obtained
by flipping all the spins in the cluster, leaving the rest of the spins to be the
same.
is obtained
by flipping all the spins in the cluster, leaving the rest of the spins to be the
same.
The correct choice of  will yield equation (12.60)
will yield equation (12.60)
 | (14.11) |
The discussion that follows proves (14.11) and can be found in the book by
Newman and Barkema [4]. The crucial observation is that the change in
energy in the exponent of the right hand side of (14.11) is due to the
creation/destruction of bonds on the boundary of the cluster. The structure of the
bonds in the interior of the cluster is identical in the two configurations  and
and
 . This can be seen in the simple example of figure 14.1. By properly choosing
the selection probability
. This can be seen in the simple example of figure 14.1. By properly choosing
the selection probability  of the new state
of the new state  and the acceptance ratio
and the acceptance ratio
 , so that
, so that
 | (14.12) |
we will succeed in satisfying (14.11) and maximize the acceptance ratio. In fact
in our case we will find that  !
!
The selection probability  is the probability of constructing a
particular cluster and can be split in three factors:
is the probability of constructing a
particular cluster and can be split in three factors:
 | (14.13) |
The first term is the probability to start the cluster from the particular seed.
By choosing a lattice site with equal probability we obtain
 | (14.14) |
Then the cluster starts growing around its seed. The second term  is the
probability to include all cluster members found in the interior of the cluster. This
probability is complicated and depends on the size and shape of the cluster.
Fortunately, it is not important to calculate it. The reason is that in the
opposite transition
is the
probability to include all cluster members found in the interior of the cluster. This
probability is complicated and depends on the size and shape of the cluster.
Fortunately, it is not important to calculate it. The reason is that in the
opposite transition  , the corresponding term is exactly the same since
the two clusters are exactly the same (the only differ by the value of the
spin)!
, the corresponding term is exactly the same since
the two clusters are exactly the same (the only differ by the value of the
spin)!
 | (14.15) |
The third term is the most interesting one. The cluster stops growing when we
are on the boundary and say “no” to including all nearest neighbors with same
spins, which are not already in the cluster (obviously, the opposite spins are not
included). If  is the probability to include a nearest neighbor of same spin to
the cluster, the probability of saying “no” is
is the probability to include a nearest neighbor of same spin to
the cluster, the probability of saying “no” is  . Assume that we have
. Assume that we have  “bonds”
of same spins on the boundary of the cluster in the state
“bonds”
of same spins on the boundary of the cluster in the state  , and that we have
, and that we have  such bonds in the state
such bonds in the state  . In figure 14.1, for example, we have that
. In figure 14.1, for example, we have that
 and
and  . Therefore, the probability to stop the cluster in
the state
. Therefore, the probability to stop the cluster in
the state  is to say “no”
is to say “no”  times, which happens with probability
times, which happens with probability
 :
:
 | (14.16) |
Similarly, the cluster in the state  stops at the same boundary with
probability
stops at the same boundary with
probability
 | (14.17) |
Therefore
 | (14.18) |
The right hand side of the above equation depends only on the number of bonds
on the boundary of the cluster. The energy difference depends only on the
creation/destruction of bonds on the boundary of the cluster and the internal
bonds don’t make any contribution to it. Each bond created during the transition
 decreases the energy by 2 and each bond destroyed increases the energy
by 2:
decreases the energy by 2 and each bond destroyed increases the energy
by 2:
 | (14.19) |
which yields
![m− nA (μ → ν ) −2β(m −n) A(μ → ν) [ 2β ]n−m
(1 − Padd) ----------= e ⇒ ----------= e (1 − Padd) .
A (ν → μ ) A(ν → μ)](main_latex5372x.png) | (14.20) |
From the above relation we see that if we choose
 | (14.21) |
then we can also choose
 | (14.22) |
Therefore, we can make the condition (14.11) to hold by constructing a cluster
using the  given by (14.21) , flipping its spins, and always accepting the
resulting configuration as the new state.
given by (14.21) , flipping its spins, and always accepting the
resulting configuration as the new state.
Summarizing, the algorithm for the construction of a Wolff cluster consists of
the following steps:
- Choose a seed by picking a lattice site with probability
 .
This is the first new member of the cluster
.
This is the first new member of the cluster
- Repeat: For each new member of the cluster, visit its nearest neighbors
that do not already belong to the cluster. If they have the same spin,
add them to the “new members” of the cluster with probability
 .
The original spin is not a “new member” anymore
.
The original spin is not a “new member” anymore
- When there are no more “new members”, the construction of the cluster
ends
- Flip the spin of all the members of the cluster.
The algorithm is ergodic, since every state can be obtained from any other state
by constructing a series of clusters of size 1 (equivalent to single flips).
The probability  depends on the temperature
depends on the temperature  . It is quite small for
. It is quite small for
 and almost 1 for
and almost 1 for  . Therefore, in the first case the algorithm
favors very small clusters (they are of size 1 for
. Therefore, in the first case the algorithm
favors very small clusters (they are of size 1 for  ) and in the second
case it favors large clusters. In the high temperature regime, we have
almost random spin flips, like in the Metropolis algorithm. In the low
temperature regime, we have large probability of flipping the dominant cluster of
the lattice. This is clearly seen in figure 14.2, where the fraction of the
average cluster size to the lattice size
) and in the second
case it favors large clusters. In the high temperature regime, we have
almost random spin flips, like in the Metropolis algorithm. In the low
temperature regime, we have large probability of flipping the dominant cluster of
the lattice. This is clearly seen in figure 14.2, where the fraction of the
average cluster size to the lattice size  is plotted as a function of the
temperature. For small
is plotted as a function of the
temperature. For small  ,
,  whereas for large
whereas for large  ,
,  .
.
Figure 14.3 shows typical spin configurations in the high and low temperature
regimes. For small  , most of the time the algorithm chooses a lattice site
randomly and constructs a small cluster around it and flips its spins. The
Metropolis algorithm picks a lattice site randomly and flips it most of the
times. In both cases, the two algorithms function almost the same way and
construct the high temperature disordered spin configurations. For large
, most of the time the algorithm chooses a lattice site
randomly and constructs a small cluster around it and flips its spins. The
Metropolis algorithm picks a lattice site randomly and flips it most of the
times. In both cases, the two algorithms function almost the same way and
construct the high temperature disordered spin configurations. For large  ,
a typical spin configuration is a “frozen” one: A large cluster of same
spins with a few isolated thermal fluctuations of different spins. Most of
the times, the Wolff algorithm picks a seed in the dominant cluster and
the new cluster is almost the same as the dominant cluster: Most of its
sites are included with few ones excluded, which upon flipping of the
spins, they will form the new thermal fluctuations. After the flips, the old
thermal fluctuations have the same spin as the dominant cluster and they
become part of the new dominant cluster. The Metropolis algorithm picks
lattice sites randomly: When they belong to the dominant cluster they are
seldomly flipped, whereas the thermal fluctuations are flipped most of the
time. Both algorithms function similarly and have the same efficiency.
,
a typical spin configuration is a “frozen” one: A large cluster of same
spins with a few isolated thermal fluctuations of different spins. Most of
the times, the Wolff algorithm picks a seed in the dominant cluster and
the new cluster is almost the same as the dominant cluster: Most of its
sites are included with few ones excluded, which upon flipping of the
spins, they will form the new thermal fluctuations. After the flips, the old
thermal fluctuations have the same spin as the dominant cluster and they
become part of the new dominant cluster. The Metropolis algorithm picks
lattice sites randomly: When they belong to the dominant cluster they are
seldomly flipped, whereas the thermal fluctuations are flipped most of the
time. Both algorithms function similarly and have the same efficiency.
Figure 14.4 shows typical spin configurations in the critical region. These are
dominated by large clusters whose size, shape and position are random. The Wolff
algorithm constructs large clusters easily, therefore, large clusters are easily
created and destroyed in a few steps (figure 14.2 shows that  ). In
contrast, the Metropolis algorithm modifies clusters by slowly moving their
boundaries and large clusters are destroyed/created very slowly. Autocorrelation
times are expected to reduce drastically when using the Wolff algorithm in the
critical region.
). In
contrast, the Metropolis algorithm modifies clusters by slowly moving their
boundaries and large clusters are destroyed/created very slowly. Autocorrelation
times are expected to reduce drastically when using the Wolff algorithm in the
critical region.
The expectation value of the size of the Wolff clusters is a dynamical quantity.
In order to see this, we will show that in the disordered phase ( ) we have
that
) we have
that
 | (14.23) |
We take the discussion from Newmann and Barkema [4]: Create
a bond on each link of the lattice connecting two same spins with
probability  . In the end, the lattice will be divided in
. In the end, the lattice will be divided in  Wolff
clusters. Each one will consist of
Wolff
clusters. Each one will consist of  sites, whose spin is
sites, whose spin is  . Choose a lattice site
randomly and flip the spins of the cluster it belongs to. Destroy the bonds and repeat the
process .
The total magnetization is:
. Choose a lattice site
randomly and flip the spins of the cluster it belongs to. Destroy the bonds and repeat the
process .
The total magnetization is:
 | (14.24) |
and
 | (14.25) |
The values  are equally probable due to the symmetry of the model,
therefore the first term vanishes. Since
are equally probable due to the symmetry of the model,
therefore the first term vanishes. Since  , we obtain
, we obtain
 | (14.26) |
In the Wolff algorithm, the creation of a cluster is equivalent to the choice of
one of the clusters we created by following the procedure described above. The
probability of selecting the cluster  is
is
 | (14.27) |
therefore the average value of the size of the Wolff clusters will be
 | (14.28) |
By using equation (14.26) and the fact that for  we have that
we have that
 ,
therefore
,
therefore
 | (14.29) |
14.3 Implementation
In order to create a cluster around a seed, we need a memory buffer for storing
the new members of the cluster. We draw cluster sites from this buffer, and
examine whether to add their nearest neighbors to the cluster.
There are two data structures that can be used in this job. The first one is the
stack (or LIFO: last in – first out) and the second one is the queue (or FIFO: first
in – first out). They are both one dimensional arrays, the only difference is how
we draw data from them. In the case of a stack, we draw the last element that we
stored in it. In the case of the queue, we draw the first element that we stored in
it.
The stack is implemented as a one dimensional array
stack(0:N-1)
in which we “push” a new value that we want to store and we “pop” one
that we want to retrieve. We use an integer m as a pointer to the last
value that we stored in the position stack(m-1). m is also the number of
active elements in the stack. In order to push a value e into the stack
we:
- check if there exist available positions in the stack (i.e. if m<N)
- set stack(m) = e
- increase m by 1.
In order to pop a value and store it in the variable e we:
- check if the stack is non empty (i.e. if m>0)
- reduce m by 1
- set e = stack(m)
The queue implementation is different. The data topology is cyclic, as
shown in figure 14.5. We use an array queue(0:N-1) and two integers m, n
which point at the beginning and at the end of the buffer. The beginning
of the data is the element queue(m-1) and the end of the data is the
element queue(n). When the queue is empty, we have that m=n and the
same is true when it is full. Therefore we need a flag that flags whether
the queue is empty or full. In the beginning we set flag=0 (queue is
empty) .
The number (m-n) mod N is the number of stored
elements .
When the queue has data, we set flag=1. In order to store a value e into the
queue we:
- check whether the queue is full (m=n and flag=1)
- set flag=1
- set queue(m) = e
- increase m by
 .
.
In order to pop a value and store it in the variable e we:
- check whether the queue is empty (m=n and flag=0)
- set e = queue(n)
- increase n by

- if m=n set flag=0.
Summarizing, the algorithm for constructing a Wolff cluster for the Ising
model is the following:
- choose a seed by randomly picking a site with probability

- check its nearest neighbors. If they have the same spin, add them to
the cluster with probability
 . The new members of
the cluster are pushed into the stack stack(0:N-1) according to the
previous discussion
. The new members of
the cluster are pushed into the stack stack(0:N-1) according to the
previous discussion
- pop a site from the stack stack(0:N-1). If the stack is empty we stop
the construction and move on to the next step. If not, we check the
site’s nearest neighbors. If they are not already in the cluster and they
have the same spin, we add them to the cluster with probability

- record the size of the cluster and flip the spin of its members.
The choice between stack or queue is not important. The results are the
same and the performance similar. The only difference is the way that the
clusters are constructed (for the stack, the cluster increases around the
seed whereas for the queue it increases first in one direction and then in
another). The careful programmer will try both during the debugging phase
of the development. Bad random number generators can be revealed in
such a test, since the Wolff algorithm turns out to be sensitive to their
shortcomings.
14.3.1 The Program
The heart of the algorithm is coded in the
subroutine
wolff() in the file wolff.f90. Each call to wolff() constructs a Wolff cluster,
flips its spin and records its size.
The buffer stack(0:N-1) is used in order to store the new members of the
cluster. We call the function ALLOCATE for dynamically allocating the necessary
memory and use DEALLOCATE before returning to the calling program in
order to return this memory back to the system - and avoid memory
leaks.
ALLOCATE(stack(0:N-1),STAT=chk)
if(chk>0) call locerr(’allocation failure for stack in wolff’)
....
DEALLOCATE(stack)!free memory of stack
If the requested memory is not available, then chk>0 and the subroutine
locerr() stops the program.
The seed is chosen randomly by a call to ranlux:
call ranlux(r,1)
cseed = INT(N*r)+1
stack(0) = cseed
nstack = 1 !the stack has 1 member, the seed
sold = s(cseed)
snew = -s(cseed) !the new spin value of the cluster
s(cseed) = snew !we flip all new members of cluster
ncluster = 1 !size of cluster=1
The seed is stored in cseed which is immediately added to the cluster
(stack(0)=cseed). The variable nstack records the number of elements
in the stack and it is originally set equal to 1. The variable ncluster
counts the number of sites in the cluster and it is originally set equal to 1.
sold=s(cseed) is the old value of the spin of the cluster and snew=-sold
is the new one. The value of the spin of a new member of the cluster
is immediately changed (s(cseed)=snew)! This increases the efficiency
of the algorithm. By checking whether the spin of a nearest neighbor
is equal to sold, we check whether the spin is the same as that of the
cluster and if it has already been included in the cluster during a previous
check.
The loop over the new members of the cluster is summarized below:
do while(nstack > 0)
!pull a site off the stack:
nstack = nstack - 1; scluster = stack(nstack)
!check its four neighbors:
!-------------scluster + XNN:
nn = scluster + XNN; if(nn > N) nn = nn - N
if(s(nn) == sold)then
call ranlux(r,1)
if(r<padd)then
stack(nstack)=nn; nstack = nstack + 1
s(nn) =snew
ncluster =ncluster+1
endif
endif
! ... check other 3 nearest neighbors ...
enddo
The loop do while(nstack > 0) is executed while nstack>0, i.e. as long as the
stack is not empty and there exist new members in the cluster. The variable
scluster is the current site drawn from the stack in order to check its nearest
neighbors. The line nn = scluster + XNN; if(nn > N) nn = nn - N
chooses the nearest neighbor to the right and stores it in the variable nn. If
the spin s(nn) of nn is equal to sold, then this neighbor has the same
spin as that of the cluster and it has not already been included to the
cluster (otherwise its spin would have been flipped). The variable padd is
equal to  (it has been set in init) and if r<padd (which happens
with probability
(it has been set in init) and if r<padd (which happens
with probability  ), then we add nn to the cluster: We add nn to the
stack, we flip its spin (s(nn)=snew) and increase the cluster size by 1.
We repeat for the rest of the nearest neighbors. The full code is listed
below:
), then we add nn to the cluster: We add nn to the
stack, we flip its spin (s(nn)=snew) and increase the cluster size by 1.
We repeat for the rest of the nearest neighbors. The full code is listed
below:
subroutine wolff
use global_data
implicit none
integer :: cseed,nstack,sold,snew,scluster,nn,chk
integer :: ncluster
real(8) :: r
integer,allocatable :: stack(:)
!allocate stack memory:
ALLOCATE(stack(0:N-1),STAT=chk)
if(chk>0) call locerr(’allocation failure for stack in wolff’)
!choose a seed for the cluster, put it on the stack and flip it
call ranlux(r,1)
cseed = INT(N*r)+1
stack(0) = cseed
nstack = 1 !the stack has 1 member, the seed
sold = s(cseed)
snew = -s(cseed) !the new spin value of the cluster
s(cseed) = snew !we flip all new members of cluster
ncluster = 1 !size of cluster=1
!start the loop on spins in the stack:
do while(nstack > 0)
!pull a site off the stack:
nstack = nstack - 1; scluster = stack(nstack)
!check its four neighbors:
!-------------scluster + XNN:
nn = scluster + XNN; if(nn > N) nn = nn - N
if(s(nn) == sold)then
call ranlux(r,1)
if(r<padd)then
stack(nstack)=nn; nstack = nstack + 1
s(nn) =snew
ncluster =ncluster+1
endif
endif
!-------------scluster - XNN:
nn = scluster - XNN; if(nn < 1) nn = nn + N
if(s(nn) == sold)then
call ranlux(r,1)
if(r<padd)then
stack(nstack)=nn; nstack = nstack + 1
s(nn) =snew
ncluster =ncluster+1
endif
endif
!-------------scluster + YNN:
nn = scluster + YNN; if(nn > N) nn = nn - N
if(s(nn) == sold)then
call ranlux(r,1)
if(r<padd)then
stack(nstack)=nn; nstack = nstack + 1
s(nn) =snew
ncluster =ncluster+1
endif
endif
!-------------scluster - YNN:
nn = scluster - YNN; if(nn < 1) nn = nn + N
if(s(nn) == sold)then
call ranlux(r,1)
if(r<padd)then
stack(nstack)=nn; nstack = nstack + 1
s(nn) =snew
ncluster =ncluster+1
endif
endif
enddo !do while(nstack > 0)
print ’(A,I14)’,’#clu ’,ncluster
!--------------------------------------
DEALLOCATE(stack)!free memory of stack
!--------------------------------------
end subroutine wolff
In order to link the subroutine with the rest of the program so that we construct one cluster
per “sweep” ,
we modify main() accordingly:
!============== main.f90 ==================
program Ising2D
use global_data
implicit none
integer :: isweep
call init
do isweep = 1, nsweep
if(algorithm .eq. 1)then
call wolff
else
call met
endif
call measure
end do
call endsim
end program Ising2D
The (global) variable algorithm controls whether the
Wolff
or the Metropolis algorithm will be used for the spin updates. The (global)
variable padd is defined in init(). The following lines are
added: into the file global_data.f90
is defined in init(). The following lines are
added: into the file global_data.f90
real(8) :: padd
integer :: algorithm
The following lines are added to the file init.f90
algorithm=0 !default is metropolis,1 is wolff
padd = 1.0D0 - exp(-2.0D0*beta)
The following lines are added to the file options.f90
.....
select case(getopt("-hL:b:s:S:n:r:uw"))
case( ’w’ )
algorithm = 1
.....
in order to add the option -w to the command line. This option sets
algorithm=1, which makes the program run the Wolff algorithm instead of the
Metropolis. Some extra info must also be added to the help message printed by
usage and simmessage and ... we are ready! For the compilation we use the
Makefile
FC = gfortran
OBJS = global_data.o getopt.o main.o init.o met.o wolff.o \
measure.o end.o options.o ranlux.o
FFLAGS = -O2
is: $(OBJS)
$(FC) $(FFLAGS) $^ -o $@
$(OBJS): global_data.f90
options.o: getopt.f90
%.o: %.f90
$(FC) $(FFLAGS) -c -o $@ $<
The commands
> make
> ./is -h
Usage: ./is [options]
-L: Lattice length (N=L*L)
-b: beta (options beta overrides the one in config)
-s: start (0 cold, 1 hot, 2 old config.)
-S: seed (options seed overrides the one in config)
-n: number of sweeps and measurements of E and M
-w: use wolff algorithm for the updates
.......
> ./is -L 20 -b 0.44 -s 1 -S 34235322 -n 5000 -w > outL20b0.44
do the compilation, print the usage instructions of the program and perform a
test run for  ,
,  , by constructing 5000 clusters, starting from a
hot configuration and writing the data to the file outL20b0.44.
, by constructing 5000 clusters, starting from a
hot configuration and writing the data to the file outL20b0.44.
14.4 Production
In order to study the Ising model on a square lattice of given size  , we have to
perform simulations for many values of
, we have to
perform simulations for many values of  . Then, we want to study the finite
size properties and extrapolate the results to the thermodynamic limit,
by repeating the process for several values of
. Then, we want to study the finite
size properties and extrapolate the results to the thermodynamic limit,
by repeating the process for several values of  . The process is long
and ... boring. Moreover, a bored researcher makes mistakes and several
bugs can enter into her calculations. Laziness is a virtue in this case and
it is worth the trouble and the time investment in order to learn some
techniques that will make our life easier, our work more efficient, and
our results more reliable. Shell scripting can be used in order to code
repeated tasks of the command line. In its simplest form, it is just a series of
commands written into a text file. Such an example can be found in the file
run1:
. The process is long
and ... boring. Moreover, a bored researcher makes mistakes and several
bugs can enter into her calculations. Laziness is a virtue in this case and
it is worth the trouble and the time investment in order to learn some
techniques that will make our life easier, our work more efficient, and
our results more reliable. Shell scripting can be used in order to code
repeated tasks of the command line. In its simplest form, it is just a series of
commands written into a text file. Such an example can be found in the file
run1:
# ################### run1 ########################
./is -L 20 -b 0.10 -s 1 -n 5000 -w -S 3423 > outL20b0.10
./is -L 20 -b 0.20 -s 2 -n 5000 -w > outL20b0.20
./is -L 20 -b 0.30 -s 2 -n 5000 -w > outL20b0.30
./is -L 20 -b 0.40 -s 2 -n 5000 -w > outL20b0.40
./is -L 20 -b 0.42 -s 2 -n 5000 -w > outL20b0.42
./is -L 20 -b 0.44 -s 2 -n 5000 -w > outL20b0.44
./is -L 20 -b 0.46 -s 2 -n 5000 -w > outL20b0.46
./is -L 20 -b 0.48 -s 2 -n 5000 -w > outL20b0.48
./is -L 20 -b 0.50 -s 2 -n 5000 -w > outL20b0.50
./is -L 20 -b 0.60 -s 2 -n 5000 -w > outL20b0.60
./is -L 20 -b 0.70 -s 2 -n 5000 -w > outL20b0.70
The first line is a comment, since everything after a # is ignored by the shell. The
second line starts a simulation from a hot configuration (-s 1), lattice size L=20
(-L 20) and temperature  (-b 0.10). The seed for the random number
generator is set equal to 3423 (-S 3423) and we measure on 5000 Wolff clusters
(-n 5000 -w). The results, printed to the stdout, are redirected to the file
outL20b0.10 (> outL20b0.10).
(-b 0.10). The seed for the random number
generator is set equal to 3423 (-S 3423) and we measure on 5000 Wolff clusters
(-n 5000 -w). The results, printed to the stdout, are redirected to the file
outL20b0.10 (> outL20b0.10).
The next ten lines continue the simulation for  –
–  . Each
simulation starts from the configuration stored in the file conf at the end of the
previous simulation.
. Each
simulation starts from the configuration stored in the file conf at the end of the
previous simulation.
In order to run these commands, the file run1 should be given execute
permissions (only once, the permissions ... stay after that) using the command
chmod:
> chmod a+x run1
Then run1 can be executed like any other command:
> ./run1
Not bad... But we can do better! Instead of adding one line for each simulation,
we can use the programming capabilities of the shell. Let’s see how. The file run2
contains the commands:
#!/bin/tcsh -f
# ################### run2 ################################
set L = 20
set betas = (0.10 0.20 0.30 0.40 0.42 0.44 0.46 0.48 0.50\
0.60 0.70)
set start = "-s 1 -S 3423"
set nsweeps = 5000
foreach beta ($betas)
echo "L= $L beta= $beta"
./is -L $L -b $beta -n $nsweeps -w $start > outL${L}b${beta}
set start = "-s 2"
end
The first line
calls the shell tcsh in order to interpret the script. This was not necessary in
run1, since every shell can interpret the commands that it contains. But in this
case we use syntax which is special to the shell tcsh.
The second line is a comment.
The third line defines a shell variable whose name is L. Its value is set after the
= character equal to the string "20". This value is accessible by adding a $ in
front of the name of the variable. Therefore, whenever we write $L (or ${L}), the
shell substitutes the string of characters 20. For example, in place of outL${L}b
the shell constructs the string outL20b.
The fourth line defines an array, whose name is betas. The different elements
of the array can be accessed by using the syntax $betas[number], where
“number” is the array element starting from 1. In the example shown above
$betas[1]= 0.10, $betas[2]= 0.20, ..., $betas[11]= 0.70. The special
variable $#betas is the number of elements in the array, which is equal to
11. When we write $betas, the shell expands it to all the values in the
array .
The fifth line defines the variable start to be equal to the string of characters
"-s 1 -S 3423". The quotes have been put because we want it to be treated as a
single string of characters. If we omit them, then the shell treats -s, 1, -S and
3423 as separate words, and we obtain a syntax error. Everything after the
character # is a comment.
The command foreach is a way to construct a loop in tcsh. The commands
between the foreach and end repeat once for every word in the parentheses in the
foreach line. Each time, the loop variable, whose name is put after the keyword
foreach, is set equal to the next word in the parenthesis. In our case, these words
are the values of the array betas, and the loop will execute 11 times, once for
each value  ,
,  , ... ,
, ... ,  , each time with $beta set equal to one of those
values.
, each time with $beta set equal to one of those
values.
The next three lines are the commands that are repeated by the foreach loop.
The command echo “echoes” its arguments to the stdout and informs us about
the current value of the parameters used in the simulation (quite useful, especially
when the simulations take a long time). The command ./is runs the program,
each time using a different value of beta. Notice that the name of the file in which
we redirect the stdout changes each time that beta changes value. Therefore
our data will be stored in the files outL20b0.10, outL20b0.20, ...,
outL20b0.70. The third command forces the program to read the initial
configuration from the file conf. The first time that the loop is executed,
the value of start is "-s 1 -S 3423" (hot configuration, seed equal to
3423), whereas for all the next simulations, start is equal to "-s 2" (old
configuration).
We can also include a loop over many values of L as follows:
#!/bin/tcsh -f
set Ls = (10 20 40)
set betas = (0.10 0.20 0.30 0.40 0.42 0.44 0.46 0.48 0.50\
0.60 0.70)
set nsweeps = 5000
foreach L ($Ls )
set start = "-s 1 -S 3423"
foreach beta ($betas)
echo "L= $L beta= $beta"
./is -L $L -b $beta -n $nsweeps -w $start > outL${L}b${beta}
set start = "-s 2"
end
end
The array variable Ls stores as many L as we wish. Note that the definitions of
start are put in a special place (why?).
14.5 Data Analysis
Data production must be monitored by looking at the time histories of properly chosen
observables. This will allow us to spot gross mistakes and it will serve as a qualitative
check of whether the system has thermalized and how long are the autocorrelation
times. It is easy to construct time histories using gnuplot. For example, the
commands :
gnuplot> plot "<grep -v ’#’ outL40b0.44" \
u 1 with lines title "E"
gnuplot> plot "<grep -v ’#’ outL40b0.44" \
u (abs($2)) with lines title "|M|"
gnuplot> plot "<awk ’/#clu/{print $2}’ outL40b0.44" \
u 1 with lines title "n"
show us the time histories of the energy, of the (absolute value of the)
magnetization and of the size of the clusters in a simulation with  and
and
 .
.
The expectation values of the energy per link  and the
magnetization per site
and the
magnetization per site  with their errors can be calculated by the
jackknife program, which can be found in the file jack.f90 in the directory Tools
(see appendix 13.8). We compile the program into an executable file jack which
we copy into the current working directory. The expectation value
with their errors can be calculated by the
jackknife program, which can be found in the file jack.f90 in the directory Tools
(see appendix 13.8). We compile the program into an executable file jack which
we copy into the current working directory. The expectation value  can be
calculated using the command:
can be
calculated using the command:
> grep -v # outL40b0.44 |\
awk -v L=40 ’NR>500{print $1/(2*L*L)}’ | ./jack
We pass the value L=40 to the program awk by using the option -v, therefore making
possible the calculation of the ratio of the first column $1 by  . The condition
NR>500 makes the printing command to be executed only after awk reads the first 500
lines .
This way we can discard a number of thermalization sweeps. The result of the
above command is printed to the stdout as follows:
. The condition
NR>500 makes the printing command to be executed only after awk reads the first 500
lines .
This way we can discard a number of thermalization sweeps. The result of the
above command is printed to the stdout as follows:
# NDAT = 4500 data. JACK = 10 groups
# <o>, chi= (<o^2>-<o>^2)
# <o> +/- err chi +/- err
-0.71091166666 0.0024162628283 0.0015719190590 7.819205433e-05
The first three lines are the comments printed by the program jack, which
inform the user about the important parameters of the analysis. The last line
gives  and its error and then the fluctuations
and its error and then the fluctuations  and their error.
The latter must be multiplied by
and their error.
The latter must be multiplied by  , in order to obtain the specific
heat
, in order to obtain the specific
heat  and its error according to (13.29) . By adding a few more lines
to the command shown above, this multiplication can be done on the
fly:
and its error according to (13.29) . By adding a few more lines
to the command shown above, this multiplication can be done on the
fly:
> set L = 40; set b = 0.44 ; \
grep -v # outL${L}b${b} | \
awk -v L=$L ’NR>500{print $1/(2*L*L)}’ | \
./jack | grep -v # | \
awk -v L=$L -v b=$b \
’{print "e",L,b,$1,$2,b*b*L*L*$3,b*b*L*L*$4}’
Well, why all this fuzz? Notice that all the commands shown above can be given
in one single line in the command line (by removing the trailing ∖ of each line).
By recalling the command, it is easy to obtain the results for a different value of
 and/or
and/or  , by editing the values of the variables L and/or b. The result
is
, by editing the values of the variables L and/or b. The result
is
e 40 0.42 -0.619523333 0.00189807 0.311391 0.0228302
i.e.  and
and  .
.
We can work in a similar way for computing the magnetization. We have to
calculate the absolute value of the second column of the stdout of the command
./is, for every line that does not start with a #:
> set L = 40 ; set b = 0.42 ; \
grep -v # outL${L}b${b} | \
awk -v L=$L ’NR>500{m=($2>0)?$2:-$2;print m/(L*L)}’ | \
./jack | grep -v # | \
awk -v L=$L -v b=$b \
’{print "m",L,b,$1,$2,b*L*L*$3,b*L*L*$4}’
The absolute value is calculated by the expression ($2>0)?$2:-$2, and it is
stored in the variable m, which in turn is printed after being divided by  .
The result is
.
The result is
m 40 0.44 0.6250527778 0.00900370 21.8345 1.39975
which gives  and
and  .
.
Similarly we can calculate  :
:
> set L = 40 ; set b = 0.44 ; \
grep ’#clu’ outL${L}b${b} | \
awk -v L=$L ’NR>500{print $2/(L*L)}’ | \
./jack | grep -v # | \
awk -v L=$L -v b=$b ’{print "n",L,b,$1,$2}’
The result is
n 40 0.44 0.4257476389 0.01302602
which gives  .
.
All of the above commands can be summarized in the script in the file
run3:
#!/bin/tcsh -f
set Ls = (10 20 40 60 80 100)
set betas = (0.00 0.10 0.20 0.25 0.30 0.34 0.38 \
0.40 0.42 0.43 0.44 0.45 0.46 0.48 \
0.48 0.50 0.55 0.60 0.65 0.70 0.80 )
set nsweeps = 100000
foreach L ($Ls )
set start = "-s 1 -S 3423"
foreach beta ($betas)
./is -L $L -b $beta -n $nsweeps -w $start > outL${L}b${beta}
set start = "-s 2"
# Calculate <e> = <E>/(2N and c=beta^2*N*(<e^2>-<e>^2):
grep -v ’#’ outL${L}b${beta} | \
awk -v L=$L ’NR>500{print $1/(2*L*L)}’ | \
./jack | grep -v ’#’ | \
awk -v L=$L -v b=$beta \
’{print "e",L,b,$1,$2,b*b*L*L*$3,b*b*L*L*$4}’
# Calculate <m> = <|M|>/N and chi=beta*N*(<m^2>-<m>^2)
grep -v ’#’ outL${L}b${beta} | \
awk -v L=$L ’NR>500{m=($2>0)?$2:-$2;print m/(L*L)}’ | \
./jack | grep -v ’#’ | \
awk -v L=$L -v b=$beta \
’{print "m",L,b,$1,$2,b*L*L*$3,b*L*L*$4}’
end
end
The script is run with the command
> ./run3 > out &
Then, we can plot the results using
gnuplot :
set xlabel "beta"
set ylabel "<m>"
plot "<grep ’^m 10 ’ out" u 3:4:5 with errorbars title " 10"
replot "<grep ’^m 20 ’ out" u 3:4:5 with errorbars title " 20"
replot "<grep ’^m 40 ’ out" u 3:4:5 with errorbars title " 40"
replot "<grep ’^m 60 ’ out" u 3:4:5 with errorbars title " 60"
replot "<grep ’^m 80 ’ out" u 3:4:5 with errorbars title " 80"
replot "<grep ’^m 100 ’ out" u 3:4:5 with errorbars title "100"
The above commands plot the magnetization.
set ylabel "chi"
set log y
plot "<grep ’^m 10 ’ out" u 3:6:7 with errorbars title " 10"
replot "<grep ’^m 20 ’ out" u 3:6:7 with errorbars title " 20"
replot "<grep ’^m 40 ’ out" u 3:6:7 with errorbars title " 40"
replot "<grep ’^m 60 ’ out" u 3:6:7 with errorbars title " 60"
replot "<grep ’^m 80 ’ out" u 3:6:7 with errorbars title " 80"
replot "<grep ’^m 100 ’ out" u 3:6:7 with errorbars title "100"
The above commands plot the magnetic susceptibility.
set ylabel "<e>"
plot "<grep ’^e 10 ’ out" u 3:4:5 with errorbars title " 10"
replot "<grep ’^e 20 ’ out" u 3:4:5 with errorbars title " 20"
replot "<grep ’^e 40 ’ out" u 3:4:5 with errorbars title " 40"
replot "<grep ’^e 60 ’ out" u 3:4:5 with errorbars title " 60"
replot "<grep ’^e 80 ’ out" u 3:4:5 with errorbars title " 80"
replot "<grep ’^e 100 ’ out" u 3:4:5 with errorbars title "100"
The above commands plot the energy.
set ylabel "c"
plot "<grep ’^e 10 ’ out" u 3:6:7 with errorbars title " 10"
replot "<grep ’^e 20 ’ out" u 3:6:7 with errorbars title " 20"
replot "<grep ’^e 40 ’ out" u 3:6:7 with errorbars title " 40"
replot "<grep ’^e 60 ’ out" u 3:6:7 with errorbars title " 60"
replot "<grep ’^e 80 ’ out" u 3:6:7 with errorbars title " 80"
replot "<grep ’^e 100 ’ out" u 3:6:7 with errorbars title "100"
The above commands plot the specific heat.
set ylabel "<n>/N"
plot "<grep ’^n 10 ’ out" u 3:4:5 with errorbars title " 10"
replot "<grep ’^n 20 ’ out" u 3:4:5 with errorbars title " 20"
replot "<grep ’^n 40 ’ out" u 3:4:5 with errorbars title " 40"
replot "<grep ’^n 60 ’ out" u 3:4:5 with errorbars title " 60"
replot "<grep ’^n 80 ’ out" u 3:4:5 with errorbars title " 80"
replot "<grep ’^n 100 ’ out" u 3:4:5 with errorbars title "100"
The above commands plot  .
.
14.6 Autocorrelation Times
In the case of the Metropolis algorithm, the “unit of time” in the Monte Carlo
simulation is one “sweep”, which is equal to  attempted spin flips. In the case
of the Wolff algorithm, the size of the clusters is a stochastic variable, which
depends on temperature. Therefore, flipping the spins of a cluster is not a
convenient unit of time, and we define:
attempted spin flips. In the case
of the Wolff algorithm, the size of the clusters is a stochastic variable, which
depends on temperature. Therefore, flipping the spins of a cluster is not a
convenient unit of time, and we define:
 | (14.30) |
This definition of a sweep can be compared to a Metropolis sweep defined as  accepted
spin flips .
For convenience, we also use the
accepted
spin flips .
For convenience, we also use the  –dependent unit of time equal to one Wolff
cluster update. We use the notation
–dependent unit of time equal to one Wolff
cluster update. We use the notation  when the autocorrelation time of
when the autocorrelation time of  is
measured in Wolf cluster updates, and
is
measured in Wolf cluster updates, and  when using the definition (14.30) .
Their relation is:
when using the definition (14.30) .
Their relation is:
 | (14.31) |
We simulate the Ising model for  and
and  at
at
 using the Wolff algorithm. We construct
using the Wolff algorithm. We construct  Wolff clusters. The
results are written to files with names outL${L}b0.4407. We also perform
simulations using the Metropolis algorithm with
Wolff clusters. The
results are written to files with names outL${L}b0.4407. We also perform
simulations using the Metropolis algorithm with  sweeps. The results are
written to files with names outL${L}b0.4407met. The following shell script makes
life easier:
sweeps. The results are
written to files with names outL${L}b0.4407met. The following shell script makes
life easier:
#!/bin/tcsh -f
set Ls = (10 20 40 60 80 100)
set beta = 0.4407
set nsweeps = 5000000
set start = "-s 1 -S 3423"
# Wolf cluster algorithm:
foreach L ($Ls)
./is -w -L $L -b $beta -n $nsweeps $start > outL${L}b${beta}
# Mean cluster size <n>/N
grep ’#clu’ outL${L}b${beta} | \
awk -v L=$L ’NR>10000{print $2/(L*L)}’ | \
./jack -d $nsweeps | grep -v ’#’ | \
awk -v L=$L -v b=$beta ’{print "n",L,b,$1,$2}’
end
# Metropolis algorithm
set nsweeps = 10000000
foreach L ($Ls)
./is -L $L -b $beta -n $nsweeps $start > outL${L}b${beta}met
end
We compile the file autoc.f90 from the Tools directory and the executable
file is named autoc and copied to the current working directory. Then, the
following shell script calculates the autocorrelation functions  :
:
#!/bin/tcsh -f
set Ls = (10 20 40 60 80 100)
set b = 0.4407
# Wolff
set tmax = 1000
set ndata = 5000000
foreach L ($Ls)
set f = outL${L}b${b}
grep -v ’#’ $f | \
awk -v L=$L \
’BEGIN{N=L*L}NR>100000{print ($2>0)?($2/N):(-$2/N)}’|\
./autoc -t $tmax -n $ndata> $f.rhom
end
# Metropolis
set tmax = 8000
set ndata = 10000000
foreach L ($Ls)
set f = outL${L}b${b}met
grep -v ’#’ $f | \
awk -v L=$L \
’BEGIN{N=L*L}NR>100000{print ($2>0)?($2/N):(-$2/N)}’|\
./autoc -t $tmax -n $ndata> $f.rhom
end
We throw away  sweeps for thermalization. The results are
written to files whose names have file extension .rhom. The function
sweeps for thermalization. The results are
written to files whose names have file extension .rhom. The function
 is fitted to (13.51) using three autocorrelation times according
to the discussion in appendix 13.7. The results are shown in table
14.1
is fitted to (13.51) using three autocorrelation times according
to the discussion in appendix 13.7. The results are shown in table
14.1
From (14.10) we expect that  where
where  is the dynamic exponent.
is the dynamic exponent.
 can be calculated by the gnuplot commands:
can be calculated by the gnuplot commands:
gnuplot> tau(x) = c*x**z
gnuplot> fit tau(x) "autoc.dat" u 1:2:3 via c,z
gnuplot> plot "autoc.dat" u 1:2:3 w e t "W steps ", tau(x)
gnuplot> fit tau(x) "autoc.dat" u 1:6:7 via c,z
gnuplot> plot "autoc.dat" u 1:6:7 w e t "W sweeps ", tau(x)
gnuplot> fit tau(x) "autoc.dat" u 1:8:9 via c,z
gnuplot> plot "autoc.dat" u 1:8:9 w e t "Metropolis", tau(x)
The exponent  is calculated for the Wolff algorithm in Wolff steps and Wolff
sweeps. The results are
is calculated for the Wolff algorithm in Wolff steps and Wolff
sweeps. The results are
 | (14.32) |
 | (14.33) |
 | (14.34) |
The plots are shown in figures 14.11-14.13. The values of  reported in the
bibliography are
reported in the
bibliography are  ,
,  and
and  respectively [4, 60, 67]. We
can obtain better results by increasing the statistics and the lattice size and this is
left as an exercise for the reader.
respectively [4, 60, 67]. We
can obtain better results by increasing the statistics and the lattice size and this is
left as an exercise for the reader.
We also mention the relation between the dynamic exponents given by
equations (14.32) and (14.33) . From (14.29)  , (13.10)
, (13.10)  ,
and (13.6)
,
and (13.6)  and using
and using  , valid in the critical region, we
obtain
, valid in the critical region, we
obtain
 | (14.35) |
where we assumed that  ,
,  and
and  . Therefore
. Therefore
 | (14.36) |
Using the values given in (13.12) ,  ,
,  , we obtain
, we obtain
 | (14.37) |
which is in agreement, within error, with the calculated values and the values in
the bibliography.
14.7 Temperature Scaling
In this section we will discuss the extent to which relations (14.3) – (14.5) can be used
for the calculation of the critical exponents  ,
,  and
and  . The result is that, although
using them it is possible to compute correct results, these relations are not the best
choice .
In order to see clear scaling and reduce finite size effects, we have to consider
. The result is that, although
using them it is possible to compute correct results, these relations are not the best
choice .
In order to see clear scaling and reduce finite size effects, we have to consider  and large
and large  . The results depend strongly on the choice of range of the data included
in the fits. The systematic errors are large and the results in some cases plain
wrong .
. The results depend strongly on the choice of range of the data included
in the fits. The systematic errors are large and the results in some cases plain
wrong .
We simulate the Ising model for  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 and
and  . The temperatures chosen correspond to small enough
. The temperatures chosen correspond to small enough  in order
to observe scaling. For the values of
in order
to observe scaling. For the values of  used in the simulations, see the shell
scripts in the accompanying software.
used in the simulations, see the shell
scripts in the accompanying software.
First we compute the exponent  from the relation (14.3) . For
given
from the relation (14.3) . For
given  , we fit the data for
, we fit the data for  for an appropriate range of
for an appropriate range of  to
the function
to
the function  , which has two fitting parameters,
, which has two fitting parameters,  and
and  . We
determine the range of
. We
determine the range of  where
where  gives a linear plot in a log–log
scale .
For large
gives a linear plot in a log–log
scale .
For large  , we observe deviations from the linear behavior and for very small
, we observe deviations from the linear behavior and for very small
 we observe finite size effects when
we observe finite size effects when  . As
. As  increases, finite size effects
decrease, and the data get closer to the asymptotic behavior
increases, finite size effects
decrease, and the data get closer to the asymptotic behavior  for even
smaller
for even
smaller  . The results are more clear for
. The results are more clear for  , because for
, because for  the
fluctuations near the pseudocritical temperature
the
fluctuations near the pseudocritical temperature  are larger and the
finite size effects are larger.
are larger and the
finite size effects are larger.
Table 14.2 shows the results for the exponent  for all the measured values of
for all the measured values of
 . The errors reported are the statistical errors of the fits, which are smaller
than the systematic errors coming from the choice or range of
. The errors reported are the statistical errors of the fits, which are smaller
than the systematic errors coming from the choice or range of  of the data
included in the fits. One has to vary this range as long as the
of the data
included in the fits. One has to vary this range as long as the  dof of the fit
remains acceptable, and the resulting variation in the values of the parameters has
to be included in the estimate of the error. Sometimes, this method gives an
overestimated error, and it is a matter or experience to decide which parameter
values to include in the estimate. For example, figures 14.14 and 14.15 show that
the acceptable range of fitting becomes more clear by studying
dof of the fit
remains acceptable, and the resulting variation in the values of the parameters has
to be included in the estimate of the error. Sometimes, this method gives an
overestimated error, and it is a matter or experience to decide which parameter
values to include in the estimate. For example, figures 14.14 and 14.15 show that
the acceptable range of fitting becomes more clear by studying  for
increasing
for
increasing  . As
. As  increases, the points approach the asymptotic curve
even closer. Even though for fixed
increases, the points approach the asymptotic curve
even closer. Even though for fixed  one obtains acceptable power fits
over a larger range of
one obtains acceptable power fits
over a larger range of  , by studying the large
, by studying the large  convergence, we can
determine the scaling region with higher accuracy. Another point to consider is
whether the parameters of the fits have reasonable values. For example, even
though the value of
convergence, we can
determine the scaling region with higher accuracy. Another point to consider is
whether the parameters of the fits have reasonable values. For example, even
though the value of  is unknown, it is reasonable to expect that its
value is of order
is unknown, it is reasonable to expect that its
value is of order  . By taking all these remarks into consideration we
obtain
. By taking all these remarks into consideration we
obtain
 | (14.38) |
 | (14.39) |
Next, we compute the critical exponent  using relation (14.5) . This relation is
valid as we approach the critical point from the low temperature phase,
using relation (14.5) . This relation is
valid as we approach the critical point from the low temperature phase,  or
or  . In the thermodynamic limit, the magnetization is everywhere zero for
all
. In the thermodynamic limit, the magnetization is everywhere zero for
all  . For a finite lattice
. For a finite lattice  , and it is reasonable to expect a scaling
of the form
, and it is reasonable to expect a scaling
of the form
 | (14.40) |
where  is defined so that
is defined so that
 | (14.41) |
By following the same procedure, we calculate the exponents  and
and  shown in table 14.3. By taking the systematic errors described above into
consideration, we find that
shown in table 14.3. By taking the systematic errors described above into
consideration, we find that
 | (14.42) |
 | (14.43) |
which should be compared to the expected values  .
.
The calculation of the exponent  needs special care. The expected
value is
needs special care. The expected
value is 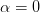 . This does not imply that
. This does not imply that  const. but that
const. but that
 | (14.44) |
In this case, we find that the data is better fitted to the above relation instead of
being fitted to a power. This can be seen pictorially by making a log–log plot and
comparing it to a  plot. We see that the second choice leads to a
better linear plot than the first one. A careful study will compute the quality of
the fits and choose the better model this way. This is left as an exercise for the
reader.
plot. We see that the second choice leads to a
better linear plot than the first one. A careful study will compute the quality of
the fits and choose the better model this way. This is left as an exercise for the
reader.
14.8 Finite Size Scaling
In this section we will calculate the critical exponents by using relations (14.7) -
(14.9) , i.e. by using the asymptotic scaling of  ,
,  and
and
 with increasing system size
with increasing system size  . This is called “finite size
scaling”.
. This is called “finite size
scaling”.
In order to calculate the exponent  given by equation (14.7) , we
calculate the magnetic susceptibility at the known
given by equation (14.7) , we
calculate the magnetic susceptibility at the known  for increasing values of
for increasing values of  .
We fit the results
.
We fit the results  to the function
to the function  and calculate the fitting
parameters
and calculate the fitting
parameters  and
and  . Then, we compare the computed value of
. Then, we compare the computed value of  to
the expected value of
to
the expected value of  . In this procedure we have to
decide which values of
. In this procedure we have to
decide which values of  should be included in the fits. The most obvious
criterion is to obtain reasonable
should be included in the fits. The most obvious
criterion is to obtain reasonable  and that the error in
and that the error in  and
and
 be small. This is not enough: Table 14.4 shows small variations in
the obtained values of
be small. This is not enough: Table 14.4 shows small variations in
the obtained values of  , if we consider different fit ranges. These
variations give an estimate of the systematic error which enters in the
calculation. Problem 9 is about trying this calculation yourselves. Table
14.4 shows the results, and figure 14.20 shows the corresponding plot.
The final result, which includes also an estimate of the systematic errors,
is
, if we consider different fit ranges. These
variations give an estimate of the systematic error which enters in the
calculation. Problem 9 is about trying this calculation yourselves. Table
14.4 shows the results, and figure 14.20 shows the corresponding plot.
The final result, which includes also an estimate of the systematic errors,
is
 | (14.45) |
For the calculation of the exponent  given by equation (14.9) , we
compute the magnetization
given by equation (14.9) , we
compute the magnetization  at the critical temperature and repeat the
same analysis. The result is
at the critical temperature and repeat the
same analysis. The result is
 | (14.46) |
Equation (14.9) gives the exponent  . But the expected value
. But the expected value  leads, in analogy with equation (14.44) , to
leads, in analogy with equation (14.44) , to
 | (14.47) |
This relation is shown in figure 14.22. The vertical axis is not in a logarithmic
scale whereas the horizontal is. The linear plot of the data shows consistency with
equation (14.47) . Problem 9 asks you to show whether the logarithmic fit is
better than a fit to a function of the form  and appreciate the difficulties
that arise in this study. By increasing the statistics, and by measuring for
larger
and appreciate the difficulties
that arise in this study. By increasing the statistics, and by measuring for
larger  , the data in table 14.8 will improve and lead to even clearer
conclusions.
, the data in table 14.8 will improve and lead to even clearer
conclusions.
We observe that, by using finite size scaling, we can compute the critical
exponents more effectively, than by using temperature scaling as in section 14.7.
The data follow the scaling relations (14.7) – (14.9) suffering smaller finite size
effects .
14.9 Calculation of 
In the previous sections we discussed scaling in  and
and  in the critical region.
In the calculations we used the exact value of the critical temperature
in the critical region.
In the calculations we used the exact value of the critical temperature
 . When
. When  is not known, the analysis becomes harder and
its computation contributes to the total error in the value of the critical
exponents. When doing finite size scaling using the scaling relations (14.7) –
(14.9) , one has to choose the values of the temperature at which to calculate the
left hand sides. So far, these values were computed at
is not known, the analysis becomes harder and
its computation contributes to the total error in the value of the critical
exponents. When doing finite size scaling using the scaling relations (14.7) –
(14.9) , one has to choose the values of the temperature at which to calculate the
left hand sides. So far, these values were computed at  . What should we do
when
. What should we do
when  is not a priori known? A good choice is to use the pseudocritical
temperature
is not a priori known? A good choice is to use the pseudocritical
temperature  , the temperature where the fluctuations of the order
parameter
, the temperature where the fluctuations of the order
parameter  are at their maximum. Otherwise, we can compute
are at their maximum. Otherwise, we can compute  according to the discussion in this section and use the computed
according to the discussion in this section and use the computed  in the finite
size scaling analysis.
in the finite
size scaling analysis.
Both choices yield the same results in the large  limit, even though the
finite size effects are different. In fact any value of
limit, even though the
finite size effects are different. In fact any value of  in the critical region can be
used for this calculation. The reason is that as we approach the critical region for
given
in the critical region can be
used for this calculation. The reason is that as we approach the critical region for
given  , the correlation length becomes
, the correlation length becomes  and finite size effects become
important. This is the behavior that characterizes the pseudocritical region of the
finite
and finite size effects become
important. This is the behavior that characterizes the pseudocritical region of the
finite  system. The pseudocritical region becomes narrower as
system. The pseudocritical region becomes narrower as  becomes
larger. Any value of
becomes
larger. Any value of  in this region will give us observables that scale at large
in this region will give us observables that scale at large
 , but the best choice is
, but the best choice is
 | (14.48) |
In this case, the values on the left hand sides of (14.7) – (14.9) should be taken
at  .
.
The definition of  in not unique. One could use, for example, the
maximum of the specific heat
in not unique. One could use, for example, the
maximum of the specific heat
 | (14.49) |
which defines a different  . Of course
. Of course 

 and both choices will yield the same results for large
and both choices will yield the same results for large  . The speed of
convergence and the errors involved in the calculation of the pseudocritical
temperatures are different in each case and there is a preferred choice, which in
our case is
. The speed of
convergence and the errors involved in the calculation of the pseudocritical
temperatures are different in each case and there is a preferred choice, which in
our case is  .
.
First we calculate  . When we are in the pseudocritical region we have that
. When we are in the pseudocritical region we have that
 , therefore (14.2) gives
, therefore (14.2) gives
 | (14.50) |
The calculation is straightforward to do: First we measure the magnetic
susceptibility. For each  we determine the pseudocritical region and
we calculate
we determine the pseudocritical region and
we calculate  and the corresponding maximum value
and the corresponding maximum value  . In
order to do that, we should take many measurements around
. In
order to do that, we should take many measurements around  . We
have to be very careful in determining the autocorrelation time (which
increases as
. We
have to be very careful in determining the autocorrelation time (which
increases as  ), so that we can control the number of independent
measurements and the thermalization of the system. We use the relation
(14.50) and fit the results to
), so that we can control the number of independent
measurements and the thermalization of the system. We use the relation
(14.50) and fit the results to  , and from the calculated parameters
, and from the calculated parameters
 and
and  we compute
we compute 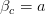 ,
,  . In cases where one of the
parameters
. In cases where one of the
parameters  ,
,  is known independently, then it is kept constant during the
fit.
is known independently, then it is kept constant during the
fit.
The results are shown in figure 14.23 where we plot the numbers contained in
table 14.5. The final result is:
This can be compared to the known values  and
and
 .
.
This process is repeated for the pseudocritical temperatures  and the
maximum values of the specific heat
and the
maximum values of the specific heat  . The results are shown in figure 14.24.
The final result is:
. The results are shown in figure 14.24.
The final result is:
Figure 14.24 and the results reported above show that the calculation using the
specific heat gives results compatible with (14.51) , but that they are less
accurate. The values of the specific heat around its maximum are more spread and
more noisy than the ones of the magnetic susceptibility.
From the maxima of the magnetic susceptibility  we can calculate the
exponent
we can calculate the
exponent  . Their values are shown in table 14.5. The data are fitted to
. Their values are shown in table 14.5. The data are fitted to  ,
according to the asymptotic relation (14.9) , with
,
according to the asymptotic relation (14.9) , with  and
and  being fitting
parameters. We find very good scaling, therefore our data are in the asymptotic
region. The result is
being fitting
parameters. We find very good scaling, therefore our data are in the asymptotic
region. The result is
 | (14.51) |
which is consistent with the analytically computed value  .
.
From the maxima of the specific heat we can calculate the exponent  .
Since
.
Since  , the form of the asymptotic behavior is given by (14.47) . We find
that our results are not very well fitted to the function
, the form of the asymptotic behavior is given by (14.47) . We find
that our results are not very well fitted to the function  and it is possible
that the discrepancy is due to finite size effects. We add terms that are subleading
in
and it is possible
that the discrepancy is due to finite size effects. We add terms that are subleading
in  and find that the fit to the function
and find that the fit to the function  is very
good .
If we attempt to fit the data to the function
is very
good .
If we attempt to fit the data to the function  , the quality of the fit
is poor and the result for
, the quality of the fit
is poor and the result for  is consistent with zero. The results are shown in
figure 14.26.
is consistent with zero. The results are shown in
figure 14.26.
14.10 Studying Scaling with Collapse
The scaling relations (14.3) – (14.9) are due to the
appearance of a unique, dynamical length scale, the correlation
length
 . As we approach the critical point,
. As we approach the critical point,  diverges as
diverges as  , and we obtain
universal behavior for all systems in the same universality class. If we consider the
magnetic susceptibility
, and we obtain
universal behavior for all systems in the same universality class. If we consider the
magnetic susceptibility  , its values depend both on the temperature
, its values depend both on the temperature  ,
the size of the system
,
the size of the system  and of course on the details of the system’s degrees of
freedom and their dynamics. Universality leads to the assumption that the
magnetic susceptibility of the infinite system in the critical region depends only on
the correlation length
and of course on the details of the system’s degrees of
freedom and their dynamics. Universality leads to the assumption that the
magnetic susceptibility of the infinite system in the critical region depends only on
the correlation length  . For the finite system in the pseudocritical region, finite
size effects suppress the fluctuations when
. For the finite system in the pseudocritical region, finite
size effects suppress the fluctuations when  . The length scales
that determine the dominant scaling behavior
. The length scales
that determine the dominant scaling behavior  are
are  and
and  ,
therefore the dimensionless variable
,
therefore the dimensionless variable  is the only independent variable in
the scaling functions. In order to obtain the scaling relation
is the only independent variable in
the scaling functions. In order to obtain the scaling relation  ,
valid for the infinite system, we only need to assume that for the finite
system
,
valid for the infinite system, we only need to assume that for the finite
system
 | (14.52) |
where  is a function of one variable, such that
is a function of one variable, such that
 | (14.53) |
and
 | (14.54) |
Indeed, when  (
( ) the magnetic susceptibility takes values very
close to those of the infinite system, and (14.53) gives
) the magnetic susceptibility takes values very
close to those of the infinite system, and (14.53) gives  . As
. As  ,
finite size effects enter and (14.54) gives
,
finite size effects enter and (14.54) gives  . The latter is
nothing but (14.7) for the maxima of the magnetic susceptibility of the finite
system that we studied in figure 14.25. Therefore the function
. The latter is
nothing but (14.7) for the maxima of the magnetic susceptibility of the finite
system that we studied in figure 14.25. Therefore the function  describes
how the magnetic susceptibility deviates from scaling due to finite size
effects.
describes
how the magnetic susceptibility deviates from scaling due to finite size
effects.
The function  can be calculated using the measurements coming from
the Monte Carlo simulation. Since the correlation length is not directly calculated,
but appears indirectly in the measurements, we define the dimensionless
variable
can be calculated using the measurements coming from
the Monte Carlo simulation. Since the correlation length is not directly calculated,
but appears indirectly in the measurements, we define the dimensionless
variable
 | (14.55) |
where  since
since
 . We define
. We define  so that (14.52) becomes
so that (14.52) becomes
 | (14.56) |
The asymptotic properties of the scaling function  are determined by the
relations (14.53) and (14.54) . When
are determined by the
relations (14.53) and (14.54) . When  , equation (14.53) is
valid for
, equation (14.53) is
valid for  and we obtain
and we obtain  From the definition
From the definition
 we obtain
we obtain  and we confirm the
scaling property of the magnetic susceptibility in the thermodynamic limit
and we confirm the
scaling property of the magnetic susceptibility in the thermodynamic limit
 . Therefore
. Therefore
 | (14.57) |
When  , (14.54) is valid and we have that
, (14.54) is valid and we have that  .
Then we obtain
.
Then we obtain  Therefore, we
confirm that, when finite size effects are dominant (
Therefore, we
confirm that, when finite size effects are dominant ( ), we have that
), we have that
 . Therefore
. Therefore
 | (14.58) |
By inverting equation (14.56) , we can calculate the scaling function from the
measurements of the magnetic susceptibility
 | (14.59) |
where  are measurements for temperatures in the pseudocritical
region for several values of
are measurements for temperatures in the pseudocritical
region for several values of  . When equation (14.59) is valid, then
all the measurements fall onto the same curve
. When equation (14.59) is valid, then
all the measurements fall onto the same curve  independently of
the size
independently of
the size  ! Of course deviations due to finite size effects are expected,
especially when
! Of course deviations due to finite size effects are expected,
especially when  is small. But, as we will see, convergence is quite
fast.
is small. But, as we will see, convergence is quite
fast.
Using the above procedure, we can determine the critical temperature  , the
exponent
, the
exponent  and the ratio
and the ratio  simultaneously! In order to check (14.59) , we
have to compute the variable
simultaneously! In order to check (14.59) , we
have to compute the variable  , for which it is necessary to
know
, for which it is necessary to
know  (
( ) and the exponent
) and the exponent  . For the calculation of
. For the calculation of
 it is necessary to know
it is necessary to know  that appears on the right hand side of
(14.59) . Relation (14.59) depends quite sensitively on the parameters
that appears on the right hand side of
(14.59) . Relation (14.59) depends quite sensitively on the parameters
 ,
,  and
and  and this way we obtain an accurate method for their
calculation.
and this way we obtain an accurate method for their
calculation.
In order to do the calculation, we set initial values for the parameters
 . Using
. Using  ,
,  ,
,  and
and  , we calculate the scaling variable
, we calculate the scaling variable
 . Using
. Using  and
and  , we calculate
, we calculate
 and plot the points
and plot the points  near the critical region
near the critical region
 . Then we vary
. Then we vary  until the curves for different
until the curves for different  collapse onto
each other. The optimal collapse determines
collapse onto
each other. The optimal collapse determines  .
.
The collapse of the curves that are constructed from the points
 for different
for different  is the most efficient
method for studying scaling in the critical region. Figure 14.27 shows the
function
is the most efficient
method for studying scaling in the critical region. Figure 14.27 shows the
function  for the known values of the parameters
for the known values of the parameters 
 . Small variations of the parameters lead to a sharp change
of the quality of the collapse. We can make a quick and dirty estimate of the
accuracy of the method by varying one of the parameters, and look for a
visible deviation from all data collapsing onto a single curve. The result is
. Small variations of the parameters lead to a sharp change
of the quality of the collapse. We can make a quick and dirty estimate of the
accuracy of the method by varying one of the parameters, and look for a
visible deviation from all data collapsing onto a single curve. The result is
Notice that, this crude estimate yields results whose accuracy is comparable to
the previously calculated ones!
A similar procedure can be followed for other scaling observables, like the
specific heat and the magnetization. Equations (14.8) and (14.9) generalize
to
 | (14.60) |
and
 | (14.61) |
since  . The results are shown in figures 14.28 and 14.29 respectively.
. The results are shown in figures 14.28 and 14.29 respectively.
Below, we list a gnuplot program in order to construct plots like the ones shown in
figures 14.27–14.29. If we assume that the data are in a file named all in the following
format :
# ##########################################################
# e L beta <e> +/- err c +/- err
# m L beta <m> +/- err chi +/- err
# n L beta <n>/N +/- err
# ----------------------------------------------------------
....
e 1000 0.462721 -0.79839031 7.506e-07 0.290266 0.00027
m 1000 0.462721 0.82648701 1.384e-06 2.137 0.00179
....
where the lines starting with the character m contain  whereas the ones starting with e contain
whereas the ones starting with e contain  . The program can
be found in the file scale_gamma.gpl:
. The program can
be found in the file scale_gamma.gpl:
# Usage:
# Ls = "40 60 80 100 120 140 160 200 500 1000"
# bc = bcc; nu = 1 ; gnu = 1.75; load "scale_gamma.gpl";
# Ls: the values of L used in the collapse
# bc: the critical temperature used in the calculation of
# t=(beta_c-beta)/beta_c
# nu: the exponent used in the calculation of x=L^{1/nu} t
# gnu: the exponent used in the calculation of
# F_chi = L^{-gnu} chi(beta,L)
#the exact critical temperature (use bc=bcc is you wish):
bcc = 0.5*log(1.0+sqrt(2.0));
NLs = words(Ls); # The number of lattice sizes
LL(i) = word (Ls,i);# Returns the i_th lattice size
cplot(i) = sprintf("\
<grep ’m %s ’ all|\
sort -k 3,3g|\
awk -v L=%s -v bc=%f -v nu=%f -v gnu=%f \
’{print L^(1.0/nu)*(bc-$3)/bc,L^(-gnu)*$6,L^(-gnu)*$7}’\
",LL(i),LL(i),bc,nu,gnu);
set macros
set term wxt enhanced
set title sprintf("b_c= %f nu= %f g/n= %f",bc,nu,gnu)
set xlabel "x=L^{1/nu} t"
set ylabel "F(x) = L^{-g/n} chi({/Symbol b},L)"
plot for[i=1:NLs] cplot(i) u 1:2:3 w e t sprintf("L=%s",LL(i))
In order to use the above program, we give the gnuplot commands
gnuplot> Ls = "40 60 80 100 120 140 160 200 500 1000"
gnuplot> bc = 0.4406868; nu = 1 ; gnu = 1.75;
gnuplot> load "scale_gamma.gpl"
The first two lines define the parameters of the plot. The variable Ls contains
all the lattice sizes that we want to study, each value of  separated
from another by one or more spaces. The variables bc, nu, gnu are the
parameters
separated
from another by one or more spaces. The variables bc, nu, gnu are the
parameters  ,
,  and
and  that will be used in the scaling relation (14.59) .
The third command calls the program that makes the plot. If we need to
vary the parameters, then we redefine the corresponding variables and ...
repeat.
that will be used in the scaling relation (14.59) .
The third command calls the program that makes the plot. If we need to
vary the parameters, then we redefine the corresponding variables and ...
repeat.
In order to dissect the above program, look at the online help manual of
gnuplot .
We will concentrate on the construction of the awk filter that computes the points
in the plot properly normalized. The value of the function cplot(i) is a string of
characters which varies with  (the index i corresponds to the i-th
word of the variable Ls). For each i, this string is substituted in the plot
command, and it is of the form "< grep ... L
(the index i corresponds to the i-th
word of the variable Ls). For each i, this string is substituted in the plot
command, and it is of the form "< grep ... L -gnu)*$7}’". The values of
the parameters are passed using the function sprintf(), which is called
each time with a different value of i. The dirty work is done by awk,
which calculates each point (columns 6 and 7: $6, $7 are
-gnu)*$7}’". The values of
the parameters are passed using the function sprintf(), which is called
each time with a different value of i. The dirty work is done by awk,
which calculates each point (columns 6 and 7: $6, $7 are  and its
error
and its
error  ). For a given value of
). For a given value of  , the grep component of the filter
prints the lines of the file all which contain the magnetization. The sort
component sorts data in the order of increasing temperature (column 3:
-k3,3g)
, the grep component of the filter
prints the lines of the file all which contain the magnetization. The sort
component sorts data in the order of increasing temperature (column 3:
-k3,3g)
Can we make the above study more systematic and apply quantitative criteria
for the quality of the collapse, which will help us estimate the error in the results?
One crude way to estimate errors is to split the data in  bins and work
independently on each set of data. Each bin will give an optimal set of
parameters
bins and work
independently on each set of data. Each bin will give an optimal set of
parameters  which will be assumed to be an independent
measurement. The errors can be calculated using equation (13.39) (for
which will be assumed to be an independent
measurement. The errors can be calculated using equation (13.39) (for
 ).
).
In order to provide a quantitative measure of the quality of the collapse, we
define a  similar to the one used in data fitting, as discussed in appendix
13.7. When the distance between the collapsing curves increases, this
similar to the one used in data fitting, as discussed in appendix
13.7. When the distance between the collapsing curves increases, this  should increase. Assume that our measurements consist of
should increase. Assume that our measurements consist of  sets of
measurements for
sets of
measurements for  . After setting the parameters
. After setting the parameters
 and an interval
and an interval ![Δx ≡ [x ,x ]
min max](main_latex5931x.png) , we calculate the data sets
, we calculate the data sets
 , for all
, for all  , using our measurements.
The data sets consist of
, using our measurements.
The data sets consist of  points of the data for
points of the data for  , for which
the
, for which
the  are in the interval
are in the interval  . For each point
. For each point  , we calculate the
scaling function
, we calculate the
scaling function  , which depends on the
chosen parameters
, which depends on the
chosen parameters  and the lattice size
and the lattice size  . Then, we have to choose
an interpolation method, which will define the interpolation functions
. Then, we have to choose
an interpolation method, which will define the interpolation functions
 ,
so that we obtain a good estimate of the scaling function between two data points.
Then, each point
,
so that we obtain a good estimate of the scaling function between two data points.
Then, each point  in a data set has a well defined distance
from every other data set
in a data set has a well defined distance
from every other data set  (
( and
and  ), which is defined by the
distance from the interpolating function of the other sets. This is equal
to
), which is defined by the
distance from the interpolating function of the other sets. This is equal
to
 . We define the quantity
. We define the quantity

where  is the number of terms in the sum. The normalization
constant
is the number of terms in the sum. The normalization
constant  is used, because this is the number of pairs of curves in the
sum. Each term is weighted by its error
is used, because this is the number of pairs of curves in the
sum. Each term is weighted by its error  , so that points with
small error have a larger contribution than points with large error. This is
the definition used in [71], but you can see other approaches in [4],
[69].
, so that points with
small error have a larger contribution than points with large error. This is
the definition used in [71], but you can see other approaches in [4],
[69].
The  depends on the parameters
depends on the parameters  and the interval
and the interval  . Initially,
we keep
. Initially,
we keep  fixed and perform a minimization with respect to the parameters
fixed and perform a minimization with respect to the parameters
 . The minimum is given by the values
. The minimum is given by the values  and these values are the
estimators that we are looking for. In order to calculate the errors
and these values are the
estimators that we are looking for. In order to calculate the errors  we can bin
our data according to the discussion on page 1663. Alternatively, we may assume
a
we can bin
our data according to the discussion on page 1663. Alternatively, we may assume
a  distribution of the measurements, and if the minimum
distribution of the measurements, and if the minimum  , then the
intervals of the parameter values that keep
, then the
intervals of the parameter values that keep  give an estimate of the errors
in the parameters.
give an estimate of the errors
in the parameters.
The results depend on the chosen interval  . Usually [69], this is chosen so
that its center is at the maximum of
. Usually [69], this is chosen so
that its center is at the maximum of  so that
so that ![Δx = [xmax − δx, xmax + δx]](main_latex5966x.png) . If
. If
 is larger than it should, then
is larger than it should, then  is large and we don’t have good
scaling. If it is too small, then the errors
is large and we don’t have good
scaling. If it is too small, then the errors  will be large. By taking the limit
will be large. By taking the limit
 , we calculate
, we calculate  by studying the convergence of
by studying the convergence of  to stable, optimal
with respect to error, values (see figure 8.7, page 238 in [4] as well as
[69]).
to stable, optimal
with respect to error, values (see figure 8.7, page 238 in [4] as well as
[69]).
14.11 Binder Cumulant
Up to now, we have studied fluctuations of observables by computing second order
cumulants .
The calculation of the critical temperature, the order of the phase transition
and the critical exponents can also be done by computing higher order
cumulants and sometimes this calculation gives more accurate and clear
results.The most famous one is the Binder cumulant which is a fourth order
cumulant ,
and its name derives from Kurt Binder who studied it first [72, 73],
 | (14.63) |
Appendix 14.12 discusses its properties in detail. For a continuous phase
transition
 | (14.64) |
where for the Ising model on a square lattice  [73]. The value
[73]. The value
 corresponds to the Gaussian distribution, whereas the value
corresponds to the Gaussian distribution, whereas the value  corresponds to two Gaussian distributions of small width around two symmetric
values
corresponds to two Gaussian distributions of small width around two symmetric
values  (see problems 14 and 15).
(see problems 14 and 15).
It practice, it is found that finite size corrections to  are small,
therefore the calculation of
are small,
therefore the calculation of  gives an accurate measurement of
the critical temperature
gives an accurate measurement of
the critical temperature  . The curves
. The curves  intersect at the point
(
intersect at the point
( ,
,  ) for different
) for different  and this point gives a very good estimate of
and this point gives a very good estimate of
 .
.
Figure 14.30 shows our measurements for  . The intersection of the
curves in the figure at a single point (
. The intersection of the
curves in the figure at a single point ( ,
,  ) is impressively accurate. Table
14.6 shows an attempt to calculate
) is impressively accurate. Table
14.6 shows an attempt to calculate  systematically by computing the critical
temperature from the intersection of the curves
systematically by computing the critical
temperature from the intersection of the curves  for three values of
for three values of  .
By taking into account all the measurements for
.
By taking into account all the measurements for  –
–  the computed
result is
the computed
result is
 | (14.65) |
which is in a very good agreement with the expected values  ,
,
 . Notice that, in the calculation of
. Notice that, in the calculation of  the systematic error
due to finite size effects decreases with increasing
the systematic error
due to finite size effects decreases with increasing  , whereas the statistical error
increases due to the increase of the slope of the curves
, whereas the statistical error
increases due to the increase of the slope of the curves  near the point
near the point
 . But the accuracy of the calculation of
. But the accuracy of the calculation of  turns out to be better with
increasing
turns out to be better with
increasing  .
.
Finite size scaling can also be applied to the Binder cumulant in order to
calculate  and
and  . From equation (14.90) (14.119) of appendix 14.12, we
expect that
. From equation (14.90) (14.119) of appendix 14.12, we
expect that  scales as
scales as
 | (14.66) |
This is confirmed in figure 14.31. From the value  , we obtain
, we obtain
 , which is consistent with the result (14.65) .
, which is consistent with the result (14.65) .
The numerical calculation of critical exponents, and especially  , can be
hard in the general case. Therefore it is desirable to cross check results using
several observables which have known scaling behavior. We discuss some of them
below .
They involve the correlations of the magnetization with the energy.
, can be
hard in the general case. Therefore it is desirable to cross check results using
several observables which have known scaling behavior. We discuss some of them
below .
They involve the correlations of the magnetization with the energy.
The derivative of the Binder cumulant is
 | (14.67) |
Its scaling is given by equation (14.120)
 | (14.68) |
which us plotted in figure 14.32. Notice that  defines a pseudocritical region
around its maximum. The scaling of the maximum as well as the scaling of its
position can be used in order to compute
defines a pseudocritical region
around its maximum. The scaling of the maximum as well as the scaling of its
position can be used in order to compute  , as we did in figures 14.23 and
14.25 for the magnetic susceptibility.
, as we did in figures 14.23 and
14.25 for the magnetic susceptibility.
It could also turn out to be useful to study correlation functions of the
form
 | (14.69) |
whose scaling properties are given by equation (14.126) of appendix
14.12,
 | (14.70) |
In particular we are interested in the case 
 | (14.71) |
and 
 | (14.72) |
We also mention the energy cumulant 
 | (14.73) |
In [76], it is shown that for a second order phase transition  ,
whereas for a first order phase transition, we obtain a non trivial value. Therefore,
this parameter can be used in order to determine whereas a system undergoes a
first order phase transition. This is confirmed in figure 14.35. The minima of the
curves
,
whereas for a first order phase transition, we obtain a non trivial value. Therefore,
this parameter can be used in order to determine whereas a system undergoes a
first order phase transition. This is confirmed in figure 14.35. The minima of the
curves  converge to the critical temperature according to (14.50)
.
converge to the critical temperature according to (14.50)
.
14.12 Appendix: Scaling
14.12.1 Binder Cumulant
In section 14.11, we studied the scaling properties of the Binder cumulant
 | (14.74) |
numerically. In this appendix, we will use the general scaling properties of a
system that undergoes a continuum phase transition near its critical temperature,
in order to derive the scaling properties of  and its derivatives. For more
details, the reader is referred to [73], [6].
and its derivatives. For more
details, the reader is referred to [73], [6].
The values of  are trivial in two cases: When the magnetization follows a
Gaussian distribution, which is true in the high temperature, disordered phase, we
have that
are trivial in two cases: When the magnetization follows a
Gaussian distribution, which is true in the high temperature, disordered phase, we
have that  . When we are in the low temperature, ordered phase, we have
that
. When we are in the low temperature, ordered phase, we have
that  . The proof is easy and it is left as an exercise (see problems 14 and
15).
. The proof is easy and it is left as an exercise (see problems 14 and
15).
According to the discussion in chapter 14, when the critical temperature  of a continuum phase transition is approached, the system exhibits scaling
properties due to the diverging correlation length
of a continuum phase transition is approached, the system exhibits scaling
properties due to the diverging correlation length  . If we approach
. If we approach  from the
high temperature phase, then we expect that the distribution function of the
magnetization per site
from the
high temperature phase, then we expect that the distribution function of the
magnetization per site  (not its absolute value) is approximately of the
form
(not its absolute value) is approximately of the
form
 | (14.75) |
which is a Gaussian with standard deviation 

 . We have
temporarily assumed that the system is defined on a
. We have
temporarily assumed that the system is defined on a  –dimensional hypercubic
lattice of edge
–dimensional hypercubic
lattice of edge  .
.
When the critical temperature is approached, the distribution function
 scales according to the relation [73]
scales according to the relation [73]
 | (14.76) |
where 

 ,
,  , is the correlation
length in the thermodynamic limit. As we approach the critical point,
, is the correlation
length in the thermodynamic limit. As we approach the critical point,
 , in such a way that
, in such a way that  . Equation (14.76) is a
scaling hypothesis which plays a fundamental role in the study of critical
phenomena.
. Equation (14.76) is a
scaling hypothesis which plays a fundamental role in the study of critical
phenomena.
In order to calculate the exponents in equation (14.76) , we apply the
normalization condition of a probability distribution function
where we set 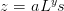 . For the left hand side to be equal to one, we must have
that
. For the left hand side to be equal to one, we must have
that  ,
,
 | (14.78) |
and  .
.  ,
,  and
and  is a constant
independent of
is a constant
independent of  and
and  . Finally, we obtain
. Finally, we obtain
 | (14.79) |
The moments of the distribution of the spins  are
are
where the last line is the definition of the function  . When we first take the
thermodynamic limit
. When we first take the
thermodynamic limit  and then approach the critical temperature
and then approach the critical temperature
 , the correlation length
, the correlation length  diverges in such a way that
diverges in such a way that  .
In the region
.
In the region  (
( ) we have that
) we have that  , and by using the
relations
, and by using the
relations
 | (14.81) |
we obtain
 | (14.82) |
In the above equations, we introduced the universal amplitudes  and
and  ,
which are universal constants (i.e. they are the same within a universality class)
and they are defined from equation (14.81) . In this limit, in order for
(14.80) to have consistent scaling for
,
which are universal constants (i.e. they are the same within a universality class)
and they are defined from equation (14.81) . In this limit, in order for
(14.80) to have consistent scaling for  on the right and left hand
sides ,
we obtain (compare with equation (14.57) )
on the right and left hand
sides ,
we obtain (compare with equation (14.57) )
 | (14.83) |
In order to compute the  -scaling, we substitute the above equations to (14.80)
for
-scaling, we substitute the above equations to (14.80)
for  , and we obtain
, and we obtain
 | (14.84) |
Then, we obtain
 | (14.85) |
where we used the known
hyperscaling relation
 | (14.86) |
Finally, we obtain the equations  ,
,
 | (14.87) |
 | (14.88) |
 | (14.89) |
which are valid in the disordered phase  . From equation (14.74) , we find
that the critical behavior of the Binder cumulant is
. From equation (14.74) , we find
that the critical behavior of the Binder cumulant is
 | (14.90) |
Finite size effects dominate in the pseudocritical region, in which case we
take the thermodynamic limit  keeping
keeping  finite, and the
fluctuations get suppressed, rendering the functions
finite, and the
fluctuations get suppressed, rendering the functions  finite. Therefore, we
obtain
finite. Therefore, we
obtain
 | (14.91) |
which shows why the value of  at the critical temperature turned out to be
almost independent of the system size
at the critical temperature turned out to be
almost independent of the system size  .
.  is found to depend on the
boundary conditions and on the anisotropy of the interaction. For the Ising model
on the square lattice we have that [73] (Kamieniarz+Blöte)
is found to depend on the
boundary conditions and on the anisotropy of the interaction. For the Ising model
on the square lattice we have that [73] (Kamieniarz+Blöte)
 | (14.92) |
14.12.2 Scaling
Consider a change of length scale on a lattice so that
 | (14.93) |
where  is the dimensionless correlation length in the thermodynamic
limit and
is the dimensionless correlation length in the thermodynamic
limit and  is the scaling factor. Then, the basic assumption for the
scaling of thermodynamics quantities in the region of a continuous
phase transition is that the free energy is changed according to
is the scaling factor. Then, the basic assumption for the
scaling of thermodynamics quantities in the region of a continuous
phase transition is that the free energy is changed according to
 | (14.94) |
where  is the reduced temperature and
is the reduced temperature and  is the external magnetic
field .
The above relation summarizes the scaling hypothesis, and it is a relation similar
to (14.76) . This relation can be understood through the renormalization group
approach, and the fundamental assumption is the appearance of a unique
dynamical length scale that diverges as we approach the critical point. The
arguments
is the external magnetic
field .
The above relation summarizes the scaling hypothesis, and it is a relation similar
to (14.76) . This relation can be understood through the renormalization group
approach, and the fundamental assumption is the appearance of a unique
dynamical length scale that diverges as we approach the critical point. The
arguments  and
and  give the change in the coupling constants
give the change in the coupling constants  and
and
 under the change in length scale in order that the equation remains
valid.
under the change in length scale in order that the equation remains
valid.
By applying the above relation  times we obtain
times we obtain
 | (14.95) |
If we take  ,
,  , keeping the product
, keeping the product 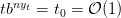 fixed, we
obtain
fixed, we
obtain
where we substituted  and defined the scaling function
and defined the scaling function  and the
critical exponent
and the
critical exponent
 | (14.97) |
By applying the same reasoning to (14.93) for the correlation length we
obtains
 | (14.98) |
By taking the limit  ,
,  , keeping the product
, keeping the product  , the left
hand side will give a finite value, e.g.
, the left
hand side will give a finite value, e.g.  whereas the right hand side will
give
whereas the right hand side will
give
 | (14.99) |
By considering the case  , and by comparing to the known relation (14.4)
, and by comparing to the known relation (14.4)
 , we obtain
, we obtain
 | (14.100) |
By taking the derivative of (14.96) with respect to the temperature, we
obtain
 | (14.101) |
We use the notation  whenever we neglect terms that are not related to the
scaling properties of a function.
whenever we neglect terms that are not related to the
scaling properties of a function.
By taking the derivative once more, and by setting  , we obtain the
specific heat
, we obtain the
specific heat
 | (14.102) |
Therefore, the critical exponent  is nothing but the critical exponent of the
specific heat defined in equation (14.4) .
is nothing but the critical exponent of the
specific heat defined in equation (14.4) .
The magnetic susceptibility can be obtained in a similar way by taking the
derivative of (14.96) with respect to 
 | (14.103) |
By taking the derivative once more time and by setting  we obtain the
magnetic susceptibility
we obtain the
magnetic susceptibility
 | (14.104) |
and, by comparing to (14.3)  , we obtain
, we obtain
 | (14.105) |
In the last two equations we used the hyperscaling relations
 | (14.106) |
14.12.3 Finite Size Scaling
We will now extend the analysis of the previous section to the case of a system of
finite size. We will assume that the system’s degrees of freedom are located on a
lattice whose linear size is  (the volume is
(the volume is  ,
,  is the number of
dimensions), where
is the number of
dimensions), where  is the (dimensionless) number of lattice sites and
is the (dimensionless) number of lattice sites and  is the
lattice constant. We consider the limit
is the
lattice constant. We consider the limit  and
and  , so that
, so that  remains
constant. By changing the
remains
constant. By changing the  -scale
-scale
 | (14.107) |
and
 | (14.108) |
equation (14.94) generalizes to
 | (14.109) |
By taking the limit  ,
,  and
and 

 (approach of the critical point), the above relation becomes
(approach of the critical point), the above relation becomes
 | (14.110) |
By differentiating and setting  as in the previous section we
obtain
as in the previous section we
obtain
 | (14.111) |
where we set  ,
, 
 .
.
The thermodynamic limit is obtained for  where
where  ,
which yields the known relation
,
which yields the known relation  .
.
When  is comparable to
is comparable to  , finite size effects dominate. The large
fluctuations are suppressed and the magnetic susceptibility has a maximum at
a crossover (pseudocritical) temperature
, finite size effects dominate. The large
fluctuations are suppressed and the magnetic susceptibility has a maximum at
a crossover (pseudocritical) temperature 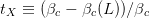 , where
, where
 . The last relation holds because
. The last relation holds because  by assumption. We
obtain
by assumption. We
obtain
 | (14.112) |
In the region of the maximum, we obtain the functional form
 | (14.113) |
which is nothing but equation (14.59) . The function  is analytic in its
argument
is analytic in its
argument  , since for a finite system
, since for a finite system  is an analytic function of the
temperature .
In the thermodynamic limit (
is an analytic function of the
temperature .
In the thermodynamic limit ( and
and  , therefore
, therefore  )
)
 | (14.114) |
so that 

 . Near the
pseudocritical point
. Near the
pseudocritical point
 | (14.115) |
and we expect that for  we have that
we have that
 | (14.116) |
The above relations lead to the following conclusions:
- The pseudocritical point shifts as
 (equation (14.50) )
(equation (14.50) )
- The peak of the magnetic susceptibility increases as

- The direction of the shifting of the maximum of the magnetic susceptibility
depends on the boundary conditions:
- Periodic boundary conditions suppress the effects of the
fluctuations, since the wave vectors are limited by
 . This
increases the pseudocritical temperature
. This
increases the pseudocritical temperature  (
(
 in (14.50) ).
in (14.50) ).
- Free boundary conditions lead to free fluctuations on the
boundary, which decrease the pseudocritical temperature
 (
(
 in (14.50) )
in (14.50) )
- Frozen (fixed) spins on the boundary lead to increased order in
the system. This increases the pseudocritical temperature
 (
(
 in (14.50) ).
in (14.50) ).
We conclude that  depends on the boundary conditions and the geometry
of the lattice.
depends on the boundary conditions and the geometry
of the lattice.
Similarly, we obtain
 | (14.117) |
and by following similar arguments leading to (14.113) , we obtain
 | (14.118) |
For the Binder cumulant we obtain
 | (14.119) |
where in the last equality we expanded the analytic functions  for
small
for
small  . Then, we see that
. Then, we see that
 | (14.120) |
By differentiating (14.110) with respect to the temperature we obtain
where we used the notation  . The term
proportional to
. The term
proportional to 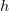 vanishes when we set
vanishes when we set  . In the pseudocritical region,
where
. In the pseudocritical region,
where  , the first and third term are of the same order in
, the first and third term are of the same order in  and we
obtain
and we
obtain
 | (14.122) |
and by successive differentiation
 | (14.123) |
The derivatives
 | (14.124) |
 | (14.125) |
In particular
 | (14.126) |
 | (14.127) |
14.13 Appendix: Critical Exponents
14.13.1 Definitions
 | (14.128) |
The scaling relation
 | (14.129) |
defines the exponents  ,
,  . The relation
. The relation
 | (14.130) |
defines the exponent  coming from the two point correlation function
coming from the two point correlation function
 .
.
14.13.2 Hyperscaling Relations
From the definitions and the hyperscaling relations we have that
 | (14.132) |
 | (14.133) |
 | (14.134) |
Table 14.7: Critical exponents of the models referred to in the first column. Whenever
the value is shown as a floating point number, the exponents are approximate. For the
approximate values we don’t apply the hyperscaling relations, but we simply mention
the values reported in the bibliography. The values for the 3d Ising model in [77] are
a conjecture. For the 3d Ising see also [43] p. 244. 3d XY and 3d AF q=3 Potts are
conjectured to belong to the same universality class.
14.14 Problems
The files all and allem in the accompanying software contain measurements
that you can use for your data analysis or compare them with your own
measurements.
- Compute the average acceptance ratio
 for the Metropolis algorithm
as a function of the temperature for
for the Metropolis algorithm
as a function of the temperature for  ,
,  ,
,  . Compute
the average size
. Compute
the average size  of the Wolff clusters at the same values of the
temperatures. Then calculate the number of Wolff clusters that are
equivalent to a Metropolis sweep. Make the plots of all of your results
and connect the points corresponding to the same
of the Wolff clusters at the same values of the
temperatures. Then calculate the number of Wolff clusters that are
equivalent to a Metropolis sweep. Make the plots of all of your results
and connect the points corresponding to the same  .
.
- Make the plots in figures 14.6–14.10 and add data for
 ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
- Make the plots in figures 14.11–14.12 and add data for
 ,
,  ,
,
 ,
,  ,
,  ,
,  . Recalculate the dynamic exponent
. Recalculate the dynamic exponent  using
your data.
using
your data.
- Make the plot in figure 14.13 and add data for
 ,
,  ,
,  ,
,  .
Recalculate the dynamic exponent
.
Recalculate the dynamic exponent  using your data.
using your data.
- Reproduce the results shown in table 14.1. Add a 6th column computing

 , where
, where  is the average acceptance
ratio of the Metropolis algorithm. This changes the unit of time to
is the average acceptance
ratio of the Metropolis algorithm. This changes the unit of time to  accepted spin flips. These are the numbers that are directly comparable
with
accepted spin flips. These are the numbers that are directly comparable
with  .
.
- Simulate the 2d Ising model on the square lattice for
 ,
,  ,
,
 ,
,  ,
,  . Choose appropriate values of
. Choose appropriate values of  , so that you will be
able to determine the magnetic susceptibility and the specific heat with
an accuracy comparable to the one shown in table 14.5. In each case,
check for the thermalization of the system and calculate the errors.
, so that you will be
able to determine the magnetic susceptibility and the specific heat with
an accuracy comparable to the one shown in table 14.5. In each case,
check for the thermalization of the system and calculate the errors.
- Make the fits that lead to the results (14.38) , (14.39) , (14.41) and
(14.43)
- Study the scaling of the specific heat as a function of the temperature.
Compare the quality of the fits to the functions
 and
and  by
computing the
by
computing the  according to the discussion in appendix 13.7
after page 1429.
according to the discussion in appendix 13.7
after page 1429.
- Consider the table 14.8 showing the measurements of
 ,
,
 and
and  . Use the values in this table in order to make the
fits which give the exponents
. Use the values in this table in order to make the
fits which give the exponents  ,
,  and
and  as described in the
text. For the exponent
as described in the
text. For the exponent  , try fitting to a power and a logarithm
and compare the results according to the discussion in the text.
, try fitting to a power and a logarithm
and compare the results according to the discussion in the text.
- Consider the table 14.5 which gives the results of the measurements of
 ,
,
 ,
,  ,
,  and
and  . Make the appropriate fits in order to
calculate the exponents
. Make the appropriate fits in order to
calculate the exponents  ,
,  ,
,  and the critical temperature
and the critical temperature  as described in the text. For the exponent
as described in the text. For the exponent  , try fitting to a power and a
logarithm and compare the results according to the discussion in the
text.
, try fitting to a power and a
logarithm and compare the results according to the discussion in the
text.
- Reproduce the collapse of the curves shown in figures 14.27-14.29. Use
the data in the file all from the accompanying software. Set the
appropriate values to the parameters and calculate the scaling functions
 . Vary each parameter separately, so that the collapse becomes
not satisfactory and use its variation as an estimate of its error.
Determine the range in
. Vary each parameter separately, so that the collapse becomes
not satisfactory and use its variation as an estimate of its error.
Determine the range in  that gives satisfactory collapse of the
curves. Repeat your calculation by performing measurements for
that gives satisfactory collapse of the
curves. Repeat your calculation by performing measurements for
 , and using the data for
, and using the data for  . Compare the
new results with the previous ones and comment on the finite size
effects.
. Compare the
new results with the previous ones and comment on the finite size
effects.
- Prove that for every observable
 we have that
we have that 

 . Using this relation
calculate the derivative of the Binder cumulant
. Using this relation
calculate the derivative of the Binder cumulant  and prove equation
(14.67) .
and prove equation
(14.67) .
- Use the maximum of the derivative of the Binder cumulant
 in order to
calculate the critical exponent
in order to
calculate the critical exponent 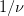 according to the analysis shown in
figures 14.23 and 14.25 for the magnetic susceptibility.
according to the analysis shown in
figures 14.23 and 14.25 for the magnetic susceptibility.
- Show that for a Gaussian distribution
 we have that
we have that
 and
and  . Conclude that
. Conclude that  .
.
- Consider the distribution given by the probability density distribution
 Plot this function and comment on the fact that it looks, qualitatively, like
the distribution of the magnetization in the low temperature phase
Plot this function and comment on the fact that it looks, qualitatively, like
the distribution of the magnetization in the low temperature phase
 . Show that
. Show that  and
and  .
Interpret your results, i.e. the meaning of each expectation value. Show
that for
.
Interpret your results, i.e. the meaning of each expectation value. Show
that for  we obtain
we obtain  . Convince yourself that the
approximation used concerns the system in the low temperature
phase.
. Convince yourself that the
approximation used concerns the system in the low temperature
phase.
- Calculate the derivative
 as a function of
as a function of  ,
,  ,
,  and
and  . Apply finite size scaling arguments and prove equation (14.120)
.
. Apply finite size scaling arguments and prove equation (14.120)
.
- Use equations (14.131) and
 ,
,  in order to prove
the other relations in (14.132) and (14.133) .
in order to prove
the other relations in (14.132) and (14.133) .
Bibliography
[Textbooks]
[1] www.physics.ntua.gr/~konstant/ComputationalPhysics/. The
site of this book. The accompanying software and additional material
can be found there. You may also find contact information about the
author for sending corrections and/or suggestions. Fan mail accepted
too!
[2] H. Gould, J. Tobochnik and H. Christian, “Computer Simulation
Methods, Application to Physical Systems”, Third Edition, Addison
Wesley (2007). A great introductory book in computational physics.
Java is the programming language of choice and a complete computing
environment is provided for using and creating interacting and visual
physics applications. The software is open source and can be downloaded
from opensourcephysics.org. The book has open access and can be
downloaded freely.
[3] R. Landau, M. J. Pez and C. C. Bordeianu, “Computational Physics:
Problem Solving with Computers”, Wiley-VCH, 2 ed. (2007).
[4] M. E. J. Newman and G. T. Barkema, “Monte Carlo Methods in
Statistical Physics”, Clarendon Press, Oxford (2002). Excellent book for
an introductory and intermediate level course in Monte Carlo methods
in physics.
[5] B. A. Berg, “Markov Chain Monte Carlo Simulations and Their
Statistical Analysis. With Web-Based Fortran Code”, World Scientific,
2004. Graduate level Monte Carlo from a great expert in the field. Covers
many advanced Monte Carlo methods.
[6] D. P. Landau and K. Binder, “A Guide to Monte Carlo Simulations
in Statistical Physics”, Cambridge University Press, 3rd Edition, 2009.
[7] K. Binder and D. W. Heermann, “Monte Carlo Simulation in
Statistical Physics”, Fifth Edition, Springer (2010).
[8] W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flanney,
“Numerical Recipes, The Art of Scientific Computing”, Third Edition,
Cambridge University Press (2007), www.nr.com. Well, this is the
handbook of every physicist in numerical methods.
[Chapter 1]
[9] M. Metcalf, J. Reid , M. Cohen, Modern Fortran Explained, 4th
Edition, OUP Oxford (2011).
[10] J. C. Adams, W. S. Brainerd, R. A. Hendrickson, R. E. Maine, J. T.
Martin and B. T. Smith, “The Fortran 2003 Handbook: The Complete
Syntax, Features and Procedures”, Springer (2009).
[11] T. M. R. Ellis, I. R. Philips and T. M. Lahey, “Fortran 90
Programming”, Addison-Wesley (1994).
[12] C. G. Page, Professional Programmer’s Guide to Fortran77,
http://www.star.le.ac.uk/~cgp/prof77.html.
[13] Gnuplot official site http://gnuplot.info/
[14] P. K. Janert, “Gnuplot in Action: Understanding Data with Graphs”,
2nd Edition, Manning Publications (2012).
[15] L. Phillips, “gnuplot Cookbook”, Packt Publishing, 2012.
[16] tcsh homepage: http://www.tcsh.org/Home
[17] P. DuBois, “Using csh & tcsh”, O’Reilly and Associates (1995),
www.kitebird.com/csh-tcsh-book/.
[18] M. J. Currie, “C-shell Cookbook”,
http://www.astro.soton.ac.uk/unixtut/sc4.pdf.
[19] Wiki book: “C Shell Scripting”,
http://en.wikibooks.org/wiki/C_Shell_Scripting.
[20] G. Anderson and P. Anderson, “The Unix C Shell Field Guide”,
Prentice Hall (1986).
[Chapter 3]
[21] R. M. May, “Simple Mathematical Models with Very Complicated
Dynamics”, Nature 261 (1976) 459. The first pedagogical and relatively
brief introduction to the logistic map and its basic properties.
[22] C. Efthimiou, “Introduction to Functional Equations: Theory and
Problem-Solving Strategies for Mathematical Competitions and Beyond”,
MSRI Mathematical Circles Library (2010). Section 16.7 presents a brief
and simple presentation of the mathematical properties of the logistic
map.
[23] P. Cvitanović, R. Artuso, R. Mainieri, G. Tanner and G. Vattay,
“Chaos: Classical and Quantum”, ChaosBook.org, Niels Bohr Institute
(2012). An excellent book on the subject. Can be freely downloaded
from the site of the book.
[24] L. Smith, “Chaos: A Very Short Introduction”, Oxford University
Press (2007).
[25] M. Schroeder, “Fractals, Chaos, Power Laws: Minutes from an
Infinite Paradise”, W.H. Freeman (1991).
[26] S. H. Strogatz, “Non Linear Dynamics and Chaos”, Addison-Wesley
(1994).
[27] Wikipedia: “Chaos Theory”, “Logistic Map”, “Bifurcation
Diagram”, “Liapunov Exponents”, “Fractal Dimension”, “Feigenbaum
constants”.
[28] Wikipedia: “List of chaotic maps”.
[29] Wikipedia: “Newton’s method”.
[30] M. Jakobson, “Absolutely continuous invariant measures for
one-parameter families of one-dimensional maps”, Commun. Math.
Phys. 81 (1981) 39.
[Chapter 4]
[31] “Numerical Recipes” [8]. See chapters on the Runge–Kutta
methods.
[32] E. W. Weisstein, “Runge-Kutta Method”, from MathWorld–A
Wolfram Web Resource.
http://mathworld.wolfram.com/Runge-KuttaMethod.html.
[33] J. H. E. Cartwright and O. Piro, “The dynamics of Runge-Kutta
methods”, Int. J. Bifurcation and Chaos 2, (1992) 427-449.
[34] J. H. Mathews, K. Fink, “Numerical Methods Using Matlab”,
Prentice Hall (2003), Chapter 9.
[35] J. H. Mathews, “Numerical Analysis - Numerical Methods Project”,
http://math.fullerton.edu/mathews/numerical.html.
[36] I. Percival and D. Richards, “Introduction to Dynamics”, Cambridge
University Press (1982). See also [38].
[37] J. B. McLaughlin, “Period Doubling bifurcations and chaotic motion
for a parametrically forced pendulum”, J. Stat. Phys. 24 (1981) 375–388.
[Chapter 5]
[38] J. V. José and E. J. Saletan, “Classical Dynamics, a Contemporary
Approach”, Cambridge University Press, 1998. A great book on Classical
Mechanics. You will find a lot of information on non linear dynamical
systems exhibiting chaotic behavior. See also the chapters on scattering
and planetary motion.
[Chapter 6]
[39] R. W. Brankin, I. Gladwell, and L. F. Shampine, “RKSUITE:
a suite of Runge-Kutta codes for the initial value problem for
ODEs”, Softreport 92-S1, Department of Mathematics, Southern
Methodist University, Dallas, Texas, U.S.A (1992). Available at
www.netlib.org/ode/rksuite and in the accompanying software of the
book.
[Chapter 9]
[40] See the Mathematica Notebooks of Peter West
http://young.physics.ucsc.edu/115/.
[41] U. Wolff, B. Bunk, F. Knechtli, “Computational Physics I”,
http://www.physik.hu-berlin.de/com/
teachingandseminars/previous_CPI_CPII.
[42] F. T. Hioe and E. W.
Montroll, “Quantum theory of anharmonic oscillators. I. Energy levels
of oscillators with positive quartic anharmonicity”, J. Math. Phys. 16
(1975) 1945, http://dx.doi.org/10.1063/1.522747
[Chapter 11]
[43] L. Kadanoff, “Statistical Physics – Statics, Dynamics and
Renormalization”, World Scientific (2000). A great book in advanced
statistical physics by one of the greatest in the field!
[44] J. Ambjørn, B. Durhuus and T. Jonsson, “Quantum Geometry”,
Cambridge Monographs on Mathematical
Physics, Cambridge University Press (1997). More in depth discussion
of random walks in field theory and statistical mechanics.
[45] C. Itzykson and J. M. Drouffe, “Statistical Field Theory”, Volume
1, Cambridge Monographs on Mathematical Physics, Cambridge
University Press (1989). Random walks and Euclidean quantum field
theory.
[46] D. E. Knuth, “Seminumerical Algorithms”, Vol. 2 of “The Art of
Computer Programming”, Addison-Wesley (1981).
[47] M. Lüscher, Comput.
Phys. Commun. 79 (1994) 100; F. James, Comput. Phys. Commun. 79
(1994) 111; Erratum 97 (1996) 357. The code is available at the journal’s
site http://cpc.cs.qub.ac.uk/summaries/ACPR_v1_0.html as well as
from CERN at
http://wwwasd.web.cern.ch/wwwasd/cernlib/
download/2001_wnt/src/mathlib/gen/v/ranlux.F.
[48] L. Schrage, “A More Portable Fortran Random Number Generator”,
ACM Transactions on Mathematical Software, 5 (1979) 132-138;
P. Bratley, B. L. Fox and L. Schrage, “A Guide to Simulation”,
Springer-Verlag, 1983.
[49] G. Marsaglia and A. Zaman, Ann. Appl. Prob. 1 (1991) 462.
[50] B. Li, N. Madras and A. D. Sokal, “Critical Exponents, Hyperscaling
and Universal Amplitude Ratios for Two-
and Three-Dimensional Self-Avoiding Walks”, J.Statist.Phys. 80 (1995)
661-754 [arXiv:hep-lat/9409003]; G. Slade, “The self-avoiding walk: A
brief survey”, Surveys in Stochastic Processes, pp. 181-199, eds. J. Blath,
P. Imkeller and S. Roelly, European Mathematical Society, Zurich,
(2011), http://www.math.ubc.ca/~slade/spa_proceedings.pdf.
[Chapter 12]
[51] J. J. Binney, N. J. Dowrick, A. J. Fisher and M. E. J. Newman,
“The Theory of Critical Phenomena”, Clarenton Press (1992). A simple
introduction to critical phenomena and the renormalization group.
[52] R. K. Pathria and P. D. Beale, “Statistical Mechanics”, Third
Edition, Elsevier (2011). A classic in statistical physics.
[53] F. Mandl, “Statistical Physics”, Second Edition, Wiley (1988).
[54] R. J. Baxter, “Exactly Solved Models in Statistical Mechanics”,
Dover Publications (2008).
[Chapter 13]
[55] E. Ising, “Beitrag zur Theorie des Ferromagnetizmus”, Z. Phys. 31
(1925) 253–258.
[56] L. Onsager, “Crystal Statistics. I. A Two–Dimensional Model with
an Order–Disorder Transition”, Phys. Rev. 65 (1944) 117–119.
[57] K. Huang, “Statistical Mechanics”, John Wiley & Sons, New York,
(1987). A detailed presentation of the Onsager solution.
[58] C. N. Yang, Phys. Rev. 85 (1952) 809.
[59] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller
and E. J. Teller, Chem. Phys. 21 (1953) 1087.
[60] M. P. Nightingale and H. W. J. Blöte, Phys. Rev. Lett. 76 (1996)
4548.
[61] H. Müller-Krumbhaar and K. Binder, J. Stat. Phys. 8 (1973) 1.
[62] B. Efron SIAM Review 21 (1979) 460; Ann. Statist. 7 (1979) 1;B.
Efron and R. Tibshirani, Statistical Science 1 (1986) 54. Freely available
from projecteuclid.org.
[Chapter 14]
[63] R. H. Swendsen and J.-S. Wang, Phys. Rev. Lett. 58 (1987) 86.
[64] U. Wolff, Phys. Rev. Lett. 62 (1989) 361.
[65] A. Pelisseto and E. Vicari, “Critical Phenomena and
Renormalization–Group Theory”, Phys. Reports 368 (2002) 549.
[66] F. Y. Wu, “The Potts Model”, Rev. Mod. Phys. 54 (1982) 235.
[67] P. D. Coddington and C. F. Baillie, Phys. Rev. Lett. 68 (1992) 962.
[68] H. Rieger, Phys. Rev. B 52 (1995) 6659.
[69] E. J. Newman and G. T. Barkema, Phys. Rev. E 53 (1996) 393.
[70] A. E. Ferdinand and M. E. Fisher, Phys. Rev. 185 (1969) 832; N.
Sh. Izmailian and C. -K. Hu, Phys. Rev. E 65 (2002) 036103; J. Salas,
J. Phys. A 34 (2001) 1311; W. Janke and R. Kenna, Nucl. Phys. (Proc.
Suppl.) 106 (2002) 929.
[71] J. Ambjørn and K. N. Anagnostopoulos, Nucl. Phys. B 497 (1997)
445.
[72] K. Binder, Phys. Rev. Lett. 47 (1981) 693.
[73] K. Binder, Z. Phys. B 43 (1981) 119; G. Kamieniarz and H. W. J.
Blöte, J. Phys. A 26 (1993) 201.
[74] J. Cardy, “Scaling and Renormalization in Statistical Physics”, 1st
Edition, Cambridge University Press (1996).
[75] A. M. Ferrenberg and D. P. Landau, Phys. Rev. B44 (1991) 5081.
[76] M. S. S. Challa, D. P. Landau and K. Binder, Phys. Rev. B34 (1986)
1841.
[77] H. E. Stanley, “Introduction to Phase Transitions and Critical
Phenomena”, Oxford (1971).
[78] R. Creswick and S.-Y. Kim, J. Phys. A: Math.Gen. 30 (1997) 8785.
[79] C. Holm and W. Janke, Phys. Rev. B 48 (1993) 936
[arXiv:hep-lat/9301002].
[80] M. Hasenbusch and S. Meyer, Phys. Lett. B 241 (1990) 238.
[81] M. Kolesik and M. Suzuki, Physica A 215 (1995) 138
[arXiv:cond-mat/9411109].
[82] M. Kolesik and M. Suzuki, Physica A 216 (1995) 469.
Index
 , 1, 2
, 1, 2
 dof, 3
dof, 3
. (current directory), 4
.. (parent directory), 5
; (separate commands), 6
$PATH, 7
- (switch, options), 8
/dev/random, 9, 10, 11
/dev/urandom, 12, 13, 14
/, 15
< (redirection), 16
>> (redirection), 17
>& (redirection), 18
> (redirection), 19
NF, 20
#!, 21
$path, 22
& (background a process), 23
a.out, 24
ar, 25
awk, 26, 27
BEGIN, 28, 29
END, 30, 31
NR, 32, 33
$1, $2, ..., 34
script, 35
cat, 36, 37
cd, 38
chmod, 39
cp, 40
date, 41
echo, 42, 43
emacs, 44
gfortran, 45, 46
link library, 47
grep, 48
head, 49
info, 50
less, 51
ls, 52
make, 53
man, 54
mkdir, 55
mv, 56
pwd, 57
rk2.csh, 58
rmdir, 59, 60
rm, 61
setenv, 62
set, 63
sort, 64
stderr, 65
stdin, 66
stdout, 67
tail, 68
time, 69
whatis, 70
where, 71
which, 72, 73
| (piping), 74, 75
absolute path, 76
acceptance ratio, 77, 78
average, 79, 80
anharmonic oscillator, 81, 82
annihilation operator, 83
attractor, 84, 85
autocorrelation
critical slowing down, 86
dynamical exponent  , 87
, 87
function, 88, 89
independent measurement, 90, 91
time, 92, 93
subdominant, 94
time, integrated, 95
basin of attraction, 96, 97, 98
bifurcation, 99, 100, 101
Binder cumulant, 102
Boltzmann constant, 103
Boltzmann distribution, 104
bootstrap, 105, 106, 107
boundary conditions
fixed, 108
free, 109
helical, 110, 111
periodic, 112, 113
toroidal, 114, 115
boundary value problem, 116
canonical ensemble, 117, 118
chaos, 119, 120, 121
period doubling, 122
pseudorandom numbers, 123
circle map, 124
cluster, 125, 126
cluster algorithms, 127
cluster seed, 128
cobweb plot, 129
cold state, 130, 131
collapse, 132
command completion, 133
command substitution, 134
completion
command, 135
filename, 136
conformable arrays, 137, 138
conjugate thermodynamic quantities, 139
continuum limit, 140
correlation function, 141, 142
correlation length, 143, 144, 145, 146
Coulomb’s law, 147
Courant parameter, 148
CPU time, 149
creation operator, 150
critical exponents, 151, 152, 153, 154
 , 155, 156, 157, 158, 159
, 155, 156, 157, 158, 159
 , 160, 161
, 160, 161
 , 162, 163
, 162, 163
 , 164, 165
, 164, 165
 , 166, 167, 168
, 166, 167, 168
 , 169, 170, 171, 172
, 169, 170, 171, 172
 , 173, 174, 175
, 173, 174, 175
 , 176, 177
, 176, 177
 , 178, 179
, 178, 179
 , 180, 181, 182
, 180, 181, 182
critical slowing down, 183, 184
cross section, 185
differential, 186, 187
total, 188
cumulant, 189
cumulative distribution function, 190
Curie temperature, 191
current directory, 192
density of states, 193
dependencies, 194
derivative
numerical, 195, 196
derivative, numerical, 197
detailed balance, 198
detailed balance condition, 199
diagonalization, 200
diffusion, 201
equation, 202
kernel, 203
Dirac delta function, 204
directory, 205
home, 206, 207
parent, 208
Dirichlet boundary condition, 209
disordered phase, 210
double well, 211, 212
DSYEV, 213
Duffing map, 214
dynamic exponent  , 215, 216
, 215, 216
dynamic memory allocation, 217
eccentricity, 218
eigenstate, 219, 220
eigenvalues, 221
eigenvectors, 222
electric equipotential surfaces, 223
electric field, 224, 225
electric field lines, 226
electric potential, 227, 228
Emacs, 229
abort command, 230, 231
auto completion, 232
commands, 233
Ctrl key, C-, 234
cut/paste, 235, 236
edit a buffer, 237
frames, 238
help, 239, 240
info, 241, 242
kill a buffer, 243
mark, 244
Meta key, M-, 245
minibuffer, 246
minibuffer, M-x, 247
modes, 248
auto fill, 249
C, 250
font lock (coloring), 251
Fortran, 252
overwrite, 253
point, 254
read a file, 255, 256, 257
recover a buffer, 258
recover file, 259
region, 260
replace, 261
save a buffer, 262, 263, 264
search, 265
spelling, 266
undo, 267, 268
window, split, 269, 270
windows, 271, 272
energy spectrum, 273
entropy, 274, 275
ergodicity, 276, 277
error
binning, 278
blocking, 279
bootstrap, 280, 281, 282
binning, 283
error of the mean, 284
integration, 285
jackknife, 286, 287
statistical, 288, 289
systematic, 290
estimator, 291, 292
Euler method, 293
Euler-Verlet method, 294, 295
expectation value, 296, 297, 298, 299
Feigenbaum constant, 300
FIFO, 301
file
owner, 302
permissions, 303
filename completion, 304
filesystem, 305
finite size effects, 306
finite size scaling, 307
first order phase transition, 308
fit, 309, 310
 dof, 311
dof, 311
variance of residuals, 312
fluctuations, 313
focus,foci, 314
foreach, 315, 316
Fortran
RANDOM_SEED, 317
RANLUX, 318, 319
allocatable, 320, 321
ALLOCATE, 322, 323, 324
ALLOCATED, 325
arrays, 326
bound upper/lower, 327
conformable, 328, 329
constructor, 330
dimension, 331, 332
DOT_PRODUCT, 333
extent, 334
LBOUND, 335
MATMUL, 336
MAXVAL, 337
MINVAL, 338
PRODUCT, 339
range, 340
rank, 341
RESHAPE, 342
scalar, 343
section, 344
shape, 345, 346
size, 347
SUM, 348
TRANSPOSE, 349
UBOUND, 350
vector operations, 351
call, 352
CMPLX, 353
column limits, 354
comments, 355
common blocks, 356, 357
comparison operators, 358
compile, 359
complex, 360
CONJG, 361
CONTAINS, 362
continuation of lines, 363
DATE_AND_TIME, 364
DBLE, 365
DEALLOCATE, 366
dimension, 367
do, 368
do while, 369, 370
DOT_PRODUCT, 371
DSYEV, 372
elemental, 373
EPSILON, 374, 375
FDATE, 376
FILE, 377
FORALL, 378
format, 379, 380
function, 381
GETARG, 382, 383
GETENV, 384
GETLOG, 385
GETOPT, 386, 387, 388
Hello World!, 389
HUGE, 390, 391
IARGC, 392
IF, 393, 394, 395
implicit, 396, 397
implied do loops, 398
INT, 399
INTERFACE, 400
intrinsic functions, 401
labeled statement, 402, 403
main program, 404
MATMUL, 405
MAXVAL, 406
MINVAL, 407
MOD, 408
module, 409, 410, 411
OPEN, 412, 413
options, 414
PACK, 415
parameter, 416
PRECISION, 417
PRODUCT, 418
RANDOM_NUMBER, 419, 420
RANDOM_SEED, 421
RANGE, 422
READ, 423
END (end of file), 424
real, 425
real, accuracy, 426
RENAME, 427
RESHAPE, 428
rksuite, 429
SAVE, 430, 431, 432
scalar, 433
SELECT, 434, 435, 436
SHAPE, 437
SIZE, 438
SLEEP, 439
STOP, 440, 441
string comparison, 442
subroutine, 443
SUM, 444, 445, 446
TINY, 447, 448
TRANSPOSE, 449
TRIM, 450, 451, 452
UBOUND, 453
unit, 454, 455
WHERE, 456
WRITE, 457
free energy, 458
Gauss map, 459
Gauss’s law, 460
Gauss-Seidel overrelaxation, 461
Gaussian distribution, 462
Gibbs, 463
Gnuplot, 464
¡, 465, 466, 467, 468
1/0 (undefined number), 469
animation, 470, 471
atan2, 472
comment, 473
fit, 474, 475, 476
functions, 477
hidden3d, 478
load, 479, 480
log plots, 481
parametric plot, 482
plot, 483
plot 3d, 484, 485, 486, 487
plot command output, 488, 489, 490, 491
plot expressions, 492, 493, 494
pm3d, 495
replot, 496, 497
reread, 498
save plots, 499
splot, 500, 501, 502, 503
using, 504, 505, 506
variables, 507, 508
with, 509
ground state, 510, 511, 512
ground state energy, 513
Hénon map, 514
hard sphere, 515
harmonic oscillator, 516, 517
heat conduction, 518
heat reservoir, 519, 520
Heisenberg’s uncertainty principle, 521
Heisenberg’s uncertainty relation, 522, 523
helical boundary conditions, 524, 525
high temperature phase, 526
histogram, 527
home directory, 528, 529
hot state, 530, 531
hyperscaling, 532
hyperscaling relations, 533, 534, 535
impact parameter, 536, 537
importance sampling, 538
independent measurement, 539, 540
initial state, 541
internal energy, 542
Ising model
 symmetry, 543, 544
symmetry, 543, 544
 , 545
, 545
energy, 546
ferromagnetic, 547
Hamiltonian, 548, 549
magnetization, 550
partition function, 551, 552
jackknife, 553, 554
Jacobi overrelaxation, 555
Kepler’s law, 556
Lapack, 557
Laplace equation, 558
lattice
constant, 559, 560
triangular, 561
leapfrog method, 562
Lennard-Jones potential, 563
Liapunov exponent, 564
libblas, 565
liblapack, 566
LIFO, 567
linear coupling, 568
logistic map, 569
 cycles, 570
cycles, 570
attractor, 571
bifurcation, 572, 573, 574
cobweb plot, 575
entropy, 576
fixed points, 577
stability, 578
onset of chaos, 579, 580
special solutions, 581
strong chaos, 582
transient behavior, 583
weak chaos, 584
low temperature phase, 585
magnetic susceptibility, 586, 587
scaling, 588, 589
magnetization, 590, 591
scaling, 592, 593
staggered, 594
magnetized, 595
Makefile, 596
man pages, 597
Markov chain, 598
Markov process, 599
Marsaglia and Zaman, 600
master equation, 601
memory
allocation, dynamic, 602
allocation, static, 603
leak, 604
Metropolis algorithm, 605
minibuffer, 606
Monte Carlo
cold state, 607, 608
hot state, 609, 610
initial state, 611, 612
simulation, 613, 614
sweep, 615, 616, 617, 618
mouse map, 619
Netlib, 620, 621
Blas, 622
Lapack, 623
DSYEV, 624
liblapack, 625
rksuite, 626
Newton’s law of gravity, 627
Newton-Raphson method, 628, 629
NRRW (non reversal random walker), 630
numerical
derivative, 631, 632, 633
integration, 634
observable, 635
Onsager, 636
exponents, 637
Onsager critical exponents, 638
options, 639, 640
order parameter, 641
ordered phase, 642
overflow, 643
overlap, 644
overrelaxation, 645, 646
parent directory, 647
parity, 648
partition function, 649
Ising model, 650
path
absolute, 651
command, 652
file, 653
relative, 654
period, 655, 656
period doubling, 657
periodic boundary conditions, 658, 659
phase transition
1st order, 660, 661
2nd order, 662
continuous, 663
piping, 664
Poincaré diagram, 665
Poisson equation, 666
pseudocritical region, 667, 668
pseudocritical temperature, 669
pseudorandom, 670
queue, 671
random
RANLUX, 672, 673
RLUXGO, 674
RLUXIN, 675
RLUXUT, 676
drandom(), 677
gaussran(), 678
naiveran(), 679
Cauchy distribution, 680
chaos, 681
correlations, 682
Gaussian distribution, 683
generator, 684
Marsaglia and Zaman, 685
modulo generator, 686
multiply-with-carry, 687
non uniform, 688
period, 689, 690, 691
pseudorandom, 692
Ranlux, 693
save state, 694, 695
Schrage, 696
seed, 697, 698
uniform, 699
urandom, 700, 701, 702
random walk, 703, 704
NRRW, 705
SAW, 706
Ranlux, 707
RANLUX, 708, 709
RLUXGO, 710, 711
RLUXIN, 712, 713
RLUXUT, 714, 715
ranlux_level, 716, 717
save state, 718
redirection, 719
relative path, 720
relativity
special, 721
reservoir, heat, 722
return probability, 723
rksuite, 724
root, 725
Runge-Kutta method, 726, 727, 728, 729, 730
adaptive stepsize, 731
Rutherford scattering, 732
RW (random walker), 733
sample, 734
sampling, 735
importance, 736
simple, 737
SAW (self avoiding walk), 738
scale invariance, 739
scaling, 740
collapse, 741
exponents, 742
factor, 743
hypothesis, 744, 745
scattering, 746, 747
rate, 748
Rutherford, 749
Schrödinger equation, 750
Schrage, 751
second order phase transition, 752
seed, 753, 754
seed of cluster, 755
selection probability, 756, 757
shell
argv, 758
array variable, 759
arrays, 760
command substitution, 761
foreach, 762
here document, 763, 764
if, 765
input $¡, 766
script, 767, 768
set, 769
tcsh, 770
variable, 771
shell script, 772
Simpson’s rule, 773
sine map, 774
SOR, successive overrelaxation, 775, 776
specific heat, 777, 778
scaling, 779, 780
spectral dimension, 781
spin
configuration, 782
spin cluster, 783, 784
splinter, 785
stack, 786
staggered, 787
standard deviation, 788
standard error, 789
standard input, 790
standard output, 791
statistical physics, 792
subdirectory, 793
successive overrelaxation, 794
susceptibility, magnetic, 795
sweep, 796, 797, 798, 799
symmetry breaking, 800
tcsh, 801
temperature, 802
tent map, 803
thermal conductivity, 804
thermal diffusivity, 805
thermalization, 806
discard, 807
time, 808
thermodynamic limit, 809
third law of thermodynamics, 810
timing jobs, 811
Tinkerbell map, 812
toroidal boundary conditions, 813, 814
transient behavior, 815, 816
transition probability, 817, 818, 819
transition rates, 820
tunneling, 821, 822
turning point, 823
universality, 824, 825, 826
class, 827
universality class, 828
user interface, 829
variables
environment, 830
shell, 831
variance, 832
wave function, 833
weights, statistical, 834
Wolff cluster algorithm, 835, 836
working directory, 837
 This book and its cover(s) are subject to copyright. They are licensed under the Creative Commons
Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit
This book and its cover(s) are subject to copyright. They are licensed under the Creative Commons
Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit  Cycles
Cycles
 Ising Model
Ising Model
 , are
, are 
 user) obtains (
user) obtains ( others) and the group (
others) and the group ( group) loose (
group) loose ( all) obtain read (
all) obtain read ( (4th column =
(4th column = 






















 and the area
and the area  of the circle and printing the results. The expressions
of the circle and printing the results. The expressions
 ,
,  .
We will store the values of the radii in an
.
We will store the values of the radii in an  . After a
check whether
. After a
check whether  , it computes the discriminant
, it computes the discriminant  by calling the
by calling the




 and
and  ,
by using double precision variables.
,
by using double precision variables.
 . We should stress that in order for two arrays to be conformable, it is not
necessary that they have the same lower and upper bounds. For example, the
command
. We should stress that in order for two arrays to be conformable, it is not
necessary that they have the same lower and upper bounds. For example, the
command 



 which is a straight line with slope 1. In order to
plot many functions simultaneously, you can write all of them in one
line:
which is a straight line with slope 1. In order to
plot many functions simultaneously, you can write all of them in one
line:
 ,
,  ,
,  and
and  .
Within the square brackets
.
Within the square brackets  and
and  axes,
respectively. The bracket
axes,
respectively. The bracket  and the bracket
and the bracket
 . You may leave the job of setting such
limits to gnuplot, by omitting some, or all of them, from the respective
positions in the brackets. For example, typing
. You may leave the job of setting such
limits to gnuplot, by omitting some, or all of them, from the respective
positions in the brackets. For example, typing  and
and  and leaves the upper and lower limits
unchanged
and leaves the upper and lower limits
unchanged , we can read their values from files.
Assume that a file
, we can read their values from files.
Assume that a file  and
and  coordinates, respectively.
The keywords
coordinates, respectively.
The keywords  to the plot
with points.
to the plot
with points.
 with a straight line
segment.
with a straight line
segment.
 . The second line
. The second line  .
.
 , where
, where  ,
,  and
and  are the numbers in the 2nd, 1st and
3rd columns respectively. The second line adds the plot of the function
are the numbers in the 2nd, 1st and
3rd columns respectively. The second line adds the plot of the function
 .
.
 .
After you make the plot, you can use the mouse in order to rotate it and view it
from a different perspective:
.
After you make the plot, you can use the mouse in order to rotate it and view it
from a different perspective: and you want to create a plot of
and you want to create a plot of
 , write the data in a file, like in the following example:
, write the data in a file, like in the following example:
 , where
, where  is a
parameter. A parametric plot in space (3-dimensions) is a surface
is a
parameter. A parametric plot in space (3-dimensions) is a surface 

 , where
, where  are parameters. The following commands
plot the circle
are parameters. The following commands
plot the circle  and the sphere
and the sphere 

 :
: arg2, then returns arg1 - arg2;
otherwise 0
arg2, then returns arg1 - arg2;
otherwise 0 
 0, then returns -arg1; else +arg1
0, then returns -arg1; else +arg1 . These, as a function of time, describe the particle’s
trajectory. The position vector is
. These, as a function of time, describe the particle’s
trajectory. The position vector is  , where
, where  and
and  are the
unit vectors on the
are the
unit vectors on the  and
and  axes respectively. The velocity vector is
axes respectively. The velocity vector is
 where
where 
 is given by
is given by 




 are known. By taking their derivatives, we
can compute the velocity and the acceleration of the particle in motion. We will
write simple programs that compute the values of these functions in a time
interval
are known. By taking their derivatives, we
can compute the velocity and the acceleration of the particle in motion. We will
write simple programs that compute the values of these functions in a time
interval ![[t0,tf]](main_latex102x.png) , where
, where  is the initial and
is the initial and  is the final time. The continuous
functions
is the final time. The continuous
functions  are approximated by a discrete sequence
of their values at the times
are approximated by a discrete sequence
of their values at the times  such that
such that
 .
.

 ,
,  , etc). The program starts by interacting with
the user (“user interface”) and asks for the values of the variables
, etc). The program starts by interacting with
the user (“user interface”) and asks for the values of the variables  ,
,
 ,
,  ,
,  ,
,  . The program prints these values to the
. The program prints these values to the  . The values
of the positions and the velocities
. The values
of the positions and the velocities  are calculated and
printed in a file together with the time
are calculated and
printed in a file together with the time  . At this point we fix the format
of the program output, something that is very important to do it in a
consistent and convenient way for easing data analysis. We choose to
print the values t, x, y, vx, vy in five columns in each line of the output
file.
. At this point we fix the format
of the program output, something that is very important to do it in a
consistent and convenient way for easing data analysis. We choose to
print the values t, x, y, vx, vy in five columns in each line of the output
file.
 and radius
and radius  with constant angular velocity
with constant angular velocity  . The position on the
circle can be defined by the angle
. The position on the
circle can be defined by the angle  , as can be seen in figure
, as can be seen in figure  to be
to be  .
.

 are
are 
 we obtain the velocity
we obtain the velocity 

 (
( ,
,  ,
,
 tangent to the trajectory) and
tangent to the trajectory) and  (
( and
and  anti-parallel,
anti-parallel,
 ).
).
 is stored
in the
is stored
in the  , the radius
, the radius  of the
circle and the angle
of the
circle and the angle  are stored in the
are stored in the  and are stored in the
and are stored in the  is calculated and stored in the
is calculated and stored in the
 in the
in the  by using the
by using the  and
and  . An
. An  or
or  the corresponding
the corresponding  is also calculated and printed for reference.
is also calculated and printed for reference.
 . The command
. The command
 ,
,  ,
,  ,
,
 ,
,  and
and  .
.
 and
and  by using the
by using the 









 . We can do that using
the raw data from the file
. We can do that using
the raw data from the file  . The function
. The function  and
and  which mark the limit values of
which mark the limit values of  . The
. The  as function of time as well as the
trajectory
as function of time as well as the
trajectory  can be plotted with the commands:
can be plotted with the commands:

 , which
is the small angle that the pendulum forms with the vertical direction.
, which
is the small angle that the pendulum forms with the vertical direction.


 and period
and period
 . The angular velocity is computed from
. The angular velocity is computed from  which gives
which gives

 and
and  . In order to
write the equations of motion in the Cartesian coordinate system shown in figure
2.6 we use the relations
. In order to
write the equations of motion in the Cartesian coordinate system shown in figure
2.6 we use the relations 
 is hard coded in the program and
that the user can only set the length
is hard coded in the program and
that the user can only set the length  of the pendulum. The data file
of the pendulum. The data file
 and the angular velocity
and the angular velocity  . The statement
. The statement
 (see the discussion
on page
(see the discussion
on page 
 is the parameter. The initial conditions are
is the parameter. The initial conditions are  ,
,
 and
and  , as shown in figure 2.7.
, as shown in figure 2.7.




 in
in
 . The program calculates
. The program calculates  and
and  and prints them to the
and prints them to the  . The
solutions to the equations of motion
. The
solutions to the equations of motion 


 ,
,  and
and  are
are
 . The full
program can be found in the file
. The full
program can be found in the file 















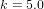

 and
and  are different in the
directions of the axes
are different in the
directions of the axes  and
and  . The solutions of the dynamical equations
of motion for
. The solutions of the dynamical equations
of motion for  ,
,  ,
,  and
and  are
are

 and
and  satisfy certain relations, the trajectories of
the particle are closed and self intersect at a given number of points.
The proof of these relations, as well as their numerical confirmation, is
left as an exercise for the reader. The program listed below is in the file
satisfy certain relations, the trajectories of
the particle are closed and self intersect at a given number of points.
The proof of these relations, as well as their numerical confirmation, is
left as an exercise for the reader. The program listed below is in the file
 in the program above. The user must enter the two angular
frequencies
in the program above. The user must enter the two angular
frequencies  and
and  and the corresponding times. A typical session for the
study of the problem is shown below:
and the corresponding times. A typical session for the
study of the problem is shown below:
 and
and  are shown in figure
are shown in figure 


 and the component of the
velocity
and the component of the
velocity  . The structure of the programs will be exactly the same as
before.
. The structure of the programs will be exactly the same as
before.

 plane with constant angular velocity
plane with constant angular velocity  . The
equations of motion are derived from the relations
. The
equations of motion are derived from the relations

 . Their solution
. Their solution



 ,
,  .
.
 ,
,  ,
the final time
,
the final time  and the time step
and the time step  . We take
. We take  . The convention that
we follow for the output of the results is that they should be written in a file
where the first 7 columns are the values of
. The convention that
we follow for the output of the results is that they should be written in a file
where the first 7 columns are the values of  ,
,  ,
,  ,
,  ,
,  ,
,  and
and
 . Each line in this file is long and, in order to prevent Fortran from
breaking it into two separate lines, we have to give an explicit format
specification. See the discussion on page
. Each line in this file is long and, in order to prevent Fortran from
breaking it into two separate lines, we have to give an explicit format
specification. See the discussion on page  ,
,  ,
,  ,
,  ,
,  ,
,  we give the following
we give the following 
















 . At time
. At time  , the particle is at
, the particle is at  and its velocity
is
and its velocity
is  , see figure
, see figure 




 and
the equations of motion are
and
the equations of motion are 


 . This choice places the center of the circle,
which is the projection of the trajectory on the
. This choice places the center of the circle,
which is the projection of the trajectory on the  plane, to be at the origin of
the coordinate system. The trajectory is a helix with radius
plane, to be at the origin of
the coordinate system. The trajectory is a helix with radius  and pitch
and pitch
 .
.
 and
and  , shown in figure
, shown in figure  (Larmor frequency). The components of the initial
velocity are
(Larmor frequency). The components of the initial
velocity are  and
and  . The initial position is calculated
from the equation
. The initial position is calculated
from the equation  . The program can be found in the file
. The program can be found in the file











 axis for
axis for  , as
can be seen in figure
, as
can be seen in figure  and
and
 it bounces and its velocity instantly reversed. Its potential energy
is
it bounces and its velocity instantly reversed. Its potential energy
is

 within the box and
within the box and  at the position of the walls.
at the position of the walls.



 as well as its velocity
as well as its velocity
 (the sign of
(the sign of  depends on the direction of the particle’s motion) at time
depends on the direction of the particle’s motion) at time
 . As long as the particle moves within the box, its motion is free and
. As long as the particle moves within the box, its motion is free and

 , so that there is no bouncing on the wall in
the time interval
, so that there is no bouncing on the wall in
the time interval  , we have that
, we have that 
 . The devil is
hiding in the word “when”. Since the time interval
. The devil is
hiding in the word “when”. Since the time interval  is finite in our program,
there is no way to know the instant of the collision with accuracy better than
is finite in our program,
there is no way to know the instant of the collision with accuracy better than
 . However, our algorithm will change the direction of the velocity
at time
. However, our algorithm will change the direction of the velocity
at time  , when the particle will have already crossed the wall.
This will introduce a systematic error, which is expected to decrease with
decreasing
, when the particle will have already crossed the wall.
This will introduce a systematic error, which is expected to decrease with
decreasing  . One way to implement the above idea is by constructing the
loop
. One way to implement the above idea is by constructing the
loop












 is shown in figure
is shown in figure  units of time. Therefore, on the plot to the right of figure
units of time. Therefore, on the plot to the right of figure  ,
,
 .
.
 . Therefore, we naively expect that
as long as we have the necessary computer power to take
. Therefore, we naively expect that
as long as we have the necessary computer power to take  as small as possible
and the corresponding time intervals as many as possible, we can achieve any
precision that we want. Well, that is true only up to a point. The problem is that
the next position is determined by the addition operation
as small as possible
and the corresponding time intervals as many as possible, we can achieve any
precision that we want. Well, that is true only up to a point. The problem is that
the next position is determined by the addition operation 

 , but some degree
of accuracy is also lost at each addition operation. And since we have
accumulation of such errors over many intervals
, but some degree
of accuracy is also lost at each addition operation. And since we have
accumulation of such errors over many intervals 

 limit
limit .
Then, the systematic error that accumulates with each addition of two numbers
with increasing difference in their orders of magnitude. This error is
.
Then, the systematic error that accumulates with each addition of two numbers
with increasing difference in their orders of magnitude. This error is  . The competition of the two effects makes the optimal choice
of
. The competition of the two effects makes the optimal choice
of  the result of a careful analysis. Such a situation is found in many
interesting problems, therefore it is quite instructive to study it in more
detail.
the result of a careful analysis. Such a situation is found in many
interesting problems, therefore it is quite instructive to study it in more
detail.
 . If the
solutions are converging in a region of values of
. If the
solutions are converging in a region of values of  , one gains confidence
that the true solution has been determined up to the accuracy of the
convergence.
, one gains confidence
that the true solution has been determined up to the accuracy of the
convergence.
 by fixing all the parameters except
by fixing all the parameters except  and then study
the dependence of the results on
and then study
the dependence of the results on  . We will take
. We will take  ,
,  ,
,
 ,
,  ,
,  , so that the particle will collide with the
wall every 10 units of time. We will measure the position of the particle
, so that the particle will collide with the
wall every 10 units of time. We will measure the position of the particle

 and study its convergence to a
limit
and study its convergence to a
limit .
.
 for
many values of
for
many values of  . We write the values of the parameters read by the program in
a file
. We write the values of the parameters read by the program in
a file  can be found
in the last line of the file
can be found
in the last line of the file  and the first two numbers coming out from
the command
and the first two numbers coming out from
the command  in the file
in the file
 reaches the
value
reaches the
value .
We do the same
.
We do the same in two new columns in the
file
in two new columns in the
file  , whereas for
, whereas for  the error becomes
the error becomes  % and the
method becomes useless. The 2nd method has much better behavior that the 1st
one.
% and the
method becomes useless. The 2nd method has much better behavior that the 1st
one.
 decreases, the final value of
decreases, the final value of  approaches the
expected
approaches the
expected  . Why don’t we obtain
. Why don’t we obtain  , especially when
, especially when  is an
integer? How many steps does it really take to reach
is an
integer? How many steps does it really take to reach  , when the expected
number of those is
, when the expected
number of those is  ? Each time you take a measurement, issue the
command
? Each time you take a measurement, issue the
command
 and in the end the difference is about 5%! Notice
that the last line should have given
and in the end the difference is about 5%! Notice
that the last line should have given  , an error
comparable to the period of the particle’s motion.
, an error
comparable to the period of the particle’s motion.
 . We can improve the accuracy of the calculation significantly if we
use the multiplication
. We can improve the accuracy of the calculation significantly if we
use the multiplication  does not
vanish completely due to the operation
does not
vanish completely due to the operation 





 and
and
 . When it reaches the boundaries of this two dimensional box, it
bounces elastically off its walls. The particle is found in an infinite depth
orthogonal potential well. The particle starts moving at time
. When it reaches the boundaries of this two dimensional box, it
bounces elastically off its walls. The particle is found in an infinite depth
orthogonal potential well. The particle starts moving at time  from
from  and our program will calculate its trajectory until time
and our program will calculate its trajectory until time  with time step
with time step  .
Such a trajectory can be seen in figure
.
Such a trajectory can be seen in figure  , then at time
, then at time
 they will be given by the relations
they will be given by the relations 













 and
and
 and which is open on the
and which is open on the  side. In the box there is a circular “hole”
with center at
side. In the box there is a circular “hole”
with center at  and radius
and radius  . If the “ball” falls in the “hole”, the player
wins. If the ball leaves out of the box through its open side, the player
loses. In order to check if the ball is in the hole when it is at position
. If the “ball” falls in the “hole”, the player
wins. If the ball leaves out of the box through its open side, the player
loses. In order to check if the ball is in the hole when it is at position
 , all we have to do is to check whether
, all we have to do is to check whether  .
.




 at time
at time  . The
player hits the ball which leaves with initial velocity of magnitude
. The
player hits the ball which leaves with initial velocity of magnitude  at an angle
at an angle
 degrees with the
degrees with the  axis. The program is found in the file
axis. The program is found in the file  and height
and height  . The collisions of
the particle with the cylinder are elastic. We take the axis of the cylinder to be
the
. The collisions of
the particle with the cylinder are elastic. We take the axis of the cylinder to be
the  axis and the two bases of the cylinder to be located at
axis and the two bases of the cylinder to be located at  and
and  .
This is shown in figure
.
This is shown in figure  plane. The projection of the particle moves within a circle of radius
plane. The projection of the particle moves within a circle of radius  and center at the intersection of the
and center at the intersection of the  axis with the plane. This is shown in
figure
axis with the plane. This is shown in
figure  component of the velocity is reflected
component of the velocity is reflected
 , whereas
, whereas  remains the same. The velocity of the particle before the
collision is
remains the same. The velocity of the particle before the
collision is 


 ,
,  , we have that
, we have that 

 , the new velocity in Cartesian coordinates
will be
, the new velocity in Cartesian coordinates
will be 









 ,
,  will be performed in the
subroutine
will be performed in the
subroutine  .
.
 in radians. The correct quadrant of the circle where
in radians. The correct quadrant of the circle where  lies
is chosen. The angle that we want to compute is given by
lies
is chosen. The angle that we want to compute is given by  , exactly on the circle.
, exactly on the circle.








 as a function of time using the command:
as a function of time using the command:
 . The cylinder (without the
bases) is given by the parametric equations
. The cylinder (without the
bases) is given by the parametric equations  with
with  ,
, ![v ∈ [0,L ]](main_latex486x.png) .
.








 with
centers at distance
with
centers at distance  like in figure
like in figure  ,
,  ,
,
 for the right circle and
for the right circle and  ,
,  ,
,
 for the left. Points on the two circles with the same
for the left. Points on the two circles with the same  are
identified. A particle entering the wormhole from the left circle with velocity
are
identified. A particle entering the wormhole from the left circle with velocity  is
immediately exiting from the right with velocity
is
immediately exiting from the right with velocity  as shown in figure
as shown in figure
 and
and  . We will use periodic
boundary conditions in order to define what happens when the
particle attempts to move outside these limits. This means that we
identify the
. We will use periodic
boundary conditions in order to define what happens when the
particle attempts to move outside these limits. This means that we
identify the  line with the
line with the  line as well as
the
line as well as
the  line with the
line with the  line. The user enters the
parameters
line. The user enters the
parameters  ,
,  and
and  as well as the initial conditions
as well as the initial conditions  ,
,
 where
where  . The user will also provide
the time parameters
. The user will also provide
the time parameters  and
and  for motion in the time interval
for motion in the time interval
![t ∈ [t = 0,t ]
0 f](main_latex518x.png) with step
with step  .
.
 ,
, 
 ,
,  in
the geometry with
in
the geometry with  .
.
 ,
,  and determine whether it is stable under small
perturbations of the initial conditions.
and determine whether it is stable under small
perturbations of the initial conditions.
 and moves in
the
and moves in
the  direction to the
direction to the  ,
,  position, draw the
trajectory and calculate the distance traveled on paper. Then confirm
your calculation from the numerical result coming from your program.
position, draw the
trajectory and calculate the distance traveled on paper. Then confirm
your calculation from the numerical result coming from your program.
 ,
,  and replot all the trajectories
mentioned above.
and replot all the trajectories
mentioned above. by the parametric equations
by the parametric equations

 by the parametric equations
by the parametric equations

 by
by 
 for given
for given  ,
,  and as long as
and as long as  . If the point
. If the point
 is outside the boundaries
is outside the boundaries  ,
,  , we redefine
, we redefine
 ,
,  in each case respectively. Points defined by the same
value of
in each case respectively. Points defined by the same
value of  are identified, i.e. they represent the
are identified, i.e. they represent the  crosses either one of the circles
crosses either one of the circles  or
or  , then we take the particle out
from the other circle.
, then we take the particle out
from the other circle.









 is determined by the relation
is determined by the relation

 is calculated from the equation
is calculated from the equation

 is mapped to the point
is mapped to the point  where
where

 , we first calculate the
vectors
, we first calculate the
vectors


 and
and  . Therefore, the
relations that give the “emerging” velocity
. Therefore, the
relations that give the “emerging” velocity  are:
are:

 and emerging from
and emerging from  .
The condition now is:
.
The condition now is:

 is given by
is given by

 is mapped to the point
is mapped to the point  where
where

 , we calculate the vectors
, we calculate the vectors


 is:
is:

 ,
,  (why?). Try to think of ways to control those errors and
study them.
(why?). Try to think of ways to control those errors and
study them.

 .
.

 and
and  respectively. They are also
unstable, as can be easily verified by using the program that you will write. The
full program is listed below:
respectively. They are also
unstable, as can be easily verified by using the program that you will write. The
full program is listed below:
 on a circle that
has the origin of the coordinate system at its center. At time
on a circle that
has the origin of the coordinate system at its center. At time  ,
the particle is at
,
the particle is at 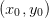 . Write the program
. Write the program  . The program should print the results
like the program
. The program should print the results
like the program  limit in the projectile motion given by equations
(
limit in the projectile motion given by equations
( and keep the non
vanishing terms as
and keep the non
vanishing terms as  . Then keep the next order leading terms
which have a smaller power of
. Then keep the next order leading terms
which have a smaller power of  . Program these relations in a file
. Program these relations in a file and calculate the range of the trajectory numerically by
using the two programs
and calculate the range of the trajectory numerically by
using the two programs  for which the two results agree within 5% accuracy.
for which the two results agree within 5% accuracy.
 . Repeat by taking the amplitude in the
. Repeat by taking the amplitude in the
 direction to be twice as much the amplitude in the
direction to be twice as much the amplitude in the  direction.
direction.
 case.
case.
 plane makes during its motion.
plane makes during its motion.

 ,
,  with the walls.
with the walls.
 ,
,  ,
,
 .
.
 . Upon reaching the ground, it bounces
inelastically such that
. Upon reaching the ground, it bounces
inelastically such that  with
with  a parameter. Write
the necessary program in order to study numerically the particle’s
motion and study the cases
a parameter. Write
the necessary program in order to study numerically the particle’s
motion and study the cases  .
.
 . Animate the calculated trajectories.
. Animate the calculated trajectories.





 of a population
of a population  is
proportional to the current population:
is
proportional to the current population:

 showing an
showing an
 an decline for
an decline for  . It is obvious that
this model is reasonable as long as the population is small enough so that the
interaction with its environment (adequate food, diseases, predators etc)
can be neglected. The simplest model that takes into account some of
the factors of the interaction with the environment (e.g. starvation) is
obtained by the introduction of a simple non linear term in the equation so
that
. It is obvious that
this model is reasonable as long as the population is small enough so that the
interaction with its environment (adequate food, diseases, predators etc)
can be neglected. The simplest model that takes into account some of
the factors of the interaction with the environment (e.g. starvation) is
obtained by the introduction of a simple non linear term in the equation so
that

 gives the maximum growth rate of the population and
gives the maximum growth rate of the population and  controls the ability of the species to maintain a certain population level. The
equation (
controls the ability of the species to maintain a certain population level. The
equation ( and that the n-th generation has population
and that the n-th generation has population  where
where  . Then
. Then  and equation (
and equation (
 . The solutions of the above equation are well approximated
by
. The solutions of the above equation are well approximated
by 
 so that we have population growth when
so that we have population growth when
 and decline when
and decline when  . Equation (
. Equation (
 we obtain the logistic map
we obtain the logistic map

 is considered as a given
parameter), so that
is considered as a given
parameter), so that

 ,
,  ,
,  ,
,
 for function composition. In what follows, the derivative of
for function composition. In what follows, the derivative of  will be
useful:
will be
useful:

 to be the fraction of the population with
respect to its maximum value, we should have
to be the fraction of the population with
respect to its maximum value, we should have  for
each
for
each . The function
. The function  has one global maximum for
has one global maximum for  which is equal
to
which is equal
to  . Therefore, if
. Therefore, if  , then
, then  , which for an
appropriate choice of
, which for an
appropriate choice of  will lead to
will lead to  for some value of
for some value of  .
Therefore, the interval of values of
.
Therefore, the interval of values of  which is of interest for our model
is
which is of interest for our model
is

 , a sequence
of values
, a sequence
of values 




 is produced. This will be
referred
is produced. This will be
referred . In the following sections we will study the properties of
these trajectories as a function of the parameter
. In the following sections we will study the properties of
these trajectories as a function of the parameter  .
.
 we have
we have 


 ,
,  whereas for
whereas for  we have periodic trajectories
resulting in rational
we have periodic trajectories
resulting in rational  and non periodic resulting in irrational
and non periodic resulting in irrational  . For other
values of
. For other
values of  we have to resort to a numerical computation of the trajectories of
the logistic map.
we have to resort to a numerical computation of the trajectories of
the logistic map.
 Cycles
Cycles is a solution of the equation
is a solution of the equation  , then
, then


 for every
for every  . For the function
. For the function  we have two solutions
we have two solutions 
 , these solutions are
, these solutions are  , the sequence
, the sequence  approaches asymptotically one of these points as
approaches asymptotically one of these points as
 . Obviously the (measure zero) sets of initial values
. Obviously the (measure zero) sets of initial values  and
and
 result in trajectories attracted by
result in trajectories attracted by  and
and  respectively. In
order to determine which one of the two values is preferred, we need to study the
respectively. In
order to determine which one of the two values is preferred, we need to study the
 and
and  . For this, assume that for some
value of
. For this, assume that for some
value of ,
,  is infinitesimally close to the fixed point
is infinitesimally close to the fixed point 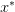 so that
so that


 about
about
 and the relation
and the relation  , we have that
, we have that  . Then we
obtain
. Then we
obtain

 we obtain
we obtain  and the fixed point
and the fixed point  is
is
 approaches
approaches  asymptotically. If
asymptotically. If  then the sequence
then the sequence  deviates away from
deviates away from  and the fixed point is
and the fixed point is
 should be studied separately
and it indicates a change in the stability properties of the fixed point. In
the following discussion, these points will be shown to be bifurcation
points.
should be studied separately
and it indicates a change in the stability properties of the fixed point. In
the following discussion, these points will be shown to be bifurcation
points. with
with  we have that
we have that
 and
and  . Therefore, if
. Therefore, if  the point
the point  is an
attractor, whereas the point
is an
attractor, whereas the point  is irrelevant. When
is irrelevant. When  ,
the point
,
the point  results in
results in  , therefore
, therefore  is unstable.
Any initial value
is unstable.
Any initial value  near
near  deviates from it. Since for
deviates from it. Since for  we
have that
we
have that  , the point
, the point  is an attractor. Any
initial value
is an attractor. Any
initial value  approaches
approaches  . When
. When  we
have the limiting case
we
have the limiting case  and we say that at the critical value
and we say that at the critical value
 the fixed point
the fixed point 
 and
and
 .
.
 increases, the fixed points continue to bifurcate. Indeed, when
increases, the fixed points continue to bifurcate. Indeed, when
 we have that
we have that  and for
and for  the point
the point  becomes unstable. Consider the solution of the equation
becomes unstable. Consider the solution of the equation  . If
. If
 is one of its solutions and for some
is one of its solutions and for some  we have that
we have that  , then
, then





 and
and 
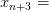



 (therefore
(therefore  is also a solution). If
is also a solution). If 
 are two such
are two such  ,
,  , then the
trajectory is periodic with period 2. The points
, then the
trajectory is periodic with period 2. The points  ,
,  are such that they are
are such that they are


 of the
equation
of the
equation , the polynomial above can be written in the form (see
, the polynomial above can be written in the form (see 
 ,
,  and
and  . The
roots of the trinomial in (
. The
roots of the trinomial in ( . For the values of
. For the values of  of interest (
of interest ( ), the
discriminant becomes positive when
), the
discriminant becomes positive when  and we have two different
solutions
and we have two different
solutions

 we have one double root, therefore a unique fixed point.
we have one double root, therefore a unique fixed point.
 requires
the same steps that led to the equation (
requires
the same steps that led to the equation ( is greater, less or equal to one. By noting
that
is greater, less or equal to one. By noting
that


 , we see that for
, we see that for
 ,
, 
 and for
and for  ,
,

 . For the intermediate values
. For the intermediate values  the
derivatives
the
derivatives  for
for  . Therefore, these points are stable
solutions of
. Therefore, these points are stable
solutions of  and the points
and the points  bifurcate to
bifurcate to  ,
,  for
for  . Almost all trajectories with initial points in the interval
. Almost all trajectories with initial points in the interval
![[0,1]](main_latex830x.png) are attracted by the periodic trajectory with period 2, the “2-cycle”
are attracted by the periodic trajectory with period 2, the “2-cycle”
 .
.
 ,
,  bifurcate to the eight fixed points
bifurcate to the eight fixed points  ,
,  when
when  .
These are real solutions of the equation that gives the 4-cycle
.
These are real solutions of the equation that gives the 4-cycle  .
For
.
For  , the points
, the points  ,
,  are a stable
4-cycle which is an attractor of almost all trajectories of the logistic
map
are a stable
4-cycle which is an attractor of almost all trajectories of the logistic
map the 16 fixed points of the equation
the 16 fixed points of the equation
 give a stable 8-cycle, for
give a stable 8-cycle, for  a stable 16-cycle
etc
a stable 16-cycle
etc are getting closer to each other as
are getting closer to each other as  increases so that
increases so that
 . As we will see,
. As we will see,  marks the onset
of the non-periodic, chaotic behavior of the trajectories of the logistic
map.
marks the onset
of the non-periodic, chaotic behavior of the trajectories of the logistic
map.








 and
and
 . The program can be found in the file
. The program can be found in the file  goes past the values
goes past the values  and
and  . Similarly, we can study
trajectories which are
. Similarly, we can study
trajectories which are  -cycles when
-cycles when  crosses the values
crosses the values  .
.

























 and we calculate the point
and we calculate the point  , where
, where
 . This point belongs on the curve
. This point belongs on the curve  . The point
. The point  is
then projected on the diagonal
is
then projected on the diagonal  and we obtain the point
and we obtain the point  . We
repeat
. We
repeat  times obtaining the points
times obtaining the points  and
and  on
on  and
and  respectively. The fixed points
respectively. The fixed points  are at the intersections of
these curves and, if they are attractors, the trajectories will converge on them. If
we have a
are at the intersections of
these curves and, if they are attractors, the trajectories will converge on them. If
we have a  -cycle, we will observe a periodic trajectory going through
points which are solutions to the equation
-cycle, we will observe a periodic trajectory going through
points which are solutions to the equation  . This exercise can
be done by using the following program, which can be found in the file
. This exercise can
be done by using the following program, which can be found in the file
 ,
,  and of the diagonal
and of the diagonal
 . Figures
. Figures  .
.

 ,
,  ,
,  and
and 
 .
For
.
For  we have
we have  fixed points
fixed points  ,
,  of
of
 . By plotting these points
. By plotting these points  as a function of
as a function of  we construct
the bifurcation diagram. These can be calculated numerically by using the
program
we construct
the bifurcation diagram. These can be calculated numerically by using the
program  that
she needs to study and for each one of them the program records the point of the
that
she needs to study and for each one of them the program records the point of the
 -cycles
-cycles ,
,  . This is easily done by computing the
logistic map several times until we are sure that the trajectories reach the stable
state. The parameter
. This is easily done by computing the
logistic map several times until we are sure that the trajectories reach the stable
state. The parameter  -cycles or depict a dense
enough set of values of the non periodic orbits. The program is listed
below:
-cycles or depict a dense
enough set of values of the non periodic orbits. The program is listed
below:








 -cycles for
-cycles for  . When
. When  goes
past
goes
past  , the trajectories become non-periodic and exhibit chaotic behavior.
Chaotic behavior will be discussed more extensively in the next section. For the
time being, we note that if we measure the distance between the points
, the trajectories become non-periodic and exhibit chaotic behavior.
Chaotic behavior will be discussed more extensively in the next section. For the
time being, we note that if we measure the distance between the points
 , we find that it decreases constantly with
, we find that it decreases constantly with  so
that
so
that

 is the Feigenbaum constant
is the Feigenbaum constant , defined by the
quotient of the separation of adjacent elements
, defined by the
quotient of the separation of adjacent elements  of period doubled attractors
from one double to the next
of period doubled attractors
from one double to the next  , is
, is

 ! By using the theorem of Sharkovskii, Li and
Yorke
! By using the theorem of Sharkovskii, Li and
Yorke in exactly the same way that we did in
equations (
in exactly the same way that we did in
equations (

 ,
,  and
and  .
The constants
.
The constants  and
and  of equations (
of equations ( and
and  . For
this reason, one has to use an approximate numerical calculation of the
roots, and the simple Newton-Raphson method will prove to be a good
choice.
. For
this reason, one has to use an approximate numerical calculation of the
roots, and the simple Newton-Raphson method will prove to be a good
choice. for the solution of the
equation
for the solution of the
equation  and computes a sequence of points
and computes a sequence of points 




 that presumably converges to one of the roots of the equation.
The computation stops at a finite
that presumably converges to one of the roots of the equation.
The computation stops at a finite  , when we decide that the desired
level of accuracy has been achieved. In order to understand how it works,
we assume that
, when we decide that the desired
level of accuracy has been achieved. In order to understand how it works,
we assume that  is an analytic function for all the values of
is an analytic function for all the values of  used in the computation. Then, by Taylor expanding around
used in the computation. Then, by Taylor expanding around  we
obtain
we
obtain

 , we choose
, we choose

 of one variable
of one variable  . Different choices for
. Different choices for  will possibly lead to
different roots. When
will possibly lead to
different roots. When  ,
,  are non zero at the root and
are non zero at the root and  is
bounded, the convergence of the method is quadratic with the number of
iterations. This means that there is a neighborhood of the root
is
bounded, the convergence of the method is quadratic with the number of
iterations. This means that there is a neighborhood of the root  such that the
distance
such that the
distance  is
is 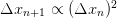 . If the root
. If the root  has multiplicity
larger than 1, convergence is slower. The proofs of these statements are simple and
can be found in
has multiplicity
larger than 1, convergence is slower. The proofs of these statements are simple and
can be found in  for some
for some  , the method
stops. For functions that tend to
, the method
stops. For functions that tend to  as
as 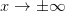 , it is easy to make a bad choice
for
, it is easy to make a bad choice
for  that does not lead to convergence to a root. Sometimes it is a
good idea to combine the Newton-Raphson method with the
that does not lead to convergence to a root. Sometimes it is a
good idea to combine the Newton-Raphson method with the  diverges at the root we might get into
trouble. For example, the equation
diverges at the root we might get into
trouble. For example, the equation  with
with  , does
not lead to a convergent sequence. In some cases, we might enter into
non-convergent cycles
, does
not lead to a convergent sequence. In some cases, we might enter into
non-convergent cycles  that will converge to the root) can be tiny. See problem
that will converge to the root) can be tiny. See problem

 in a one dimensional potential well
of depth
in a one dimensional potential well
of depth  and width
and width  . The parameters
. The parameters  and
and
 . Given
. Given  , we solve for
, we solve for  which gives the energy
which gives the energy  . The
function
. The
function  and its derivative
and its derivative  are
are 
 can be found in the file
can be found in the file  . We fix
. We fix

 . It is instructive to make the plot of the left and right hand sides
of (
. It is instructive to make the plot of the left and right hand sides
of ( .
Using
.
Using 

 .
The reader can compute more of these roots by following these steps by
herself.
.
The reader can compute more of these roots by following these steps by
herself.
 and
and  . In order to compute a sequence
. In order to compute a sequence  ,
,
 ,
,  ,
,  ,
,  ,
,  that may converge to a root
of the above system of equations, we Taylor expand the two functions around
that may converge to a root
of the above system of equations, we Taylor expand the two functions around


 and
and  and setting
and setting
 ,
,  , we obtain
, we obtain 
 system of equations
system of equations 
 and
and  , with
, with  . Solving for
. Solving for  we obtain
we obtain

 become small enough.
become small enough.
 ,
,
 . We have
. We have  ,
,  ,
,  ,
,
 . The program can be found in the file
. The program can be found in the file  together with the plane
together with the plane  . The intersection
of the three surfaces determine the roots we are looking for. Compiling and
running the program can be done by using the commands:
. The intersection
of the three surfaces determine the roots we are looking for. Compiling and
running the program can be done by using the commands:

 ,
,

 ,
, 
 .
.
 we will solve the algebraic
equations
we will solve the algebraic
equations  and
and  . At these points,
. At these points,  -cycles
become unstable and
-cycles
become unstable and  -cycles appear and are stable. This happens when
-cycles appear and are stable. This happens when
 , where
, where  . We will look for solutions
. We will look for solutions  for
for
 .
.
 and
and  as in equation (
as in equation (



 by a routine that will compose the function
by a routine that will compose the function 
 -times. The
program can be found in the file
-times. The
program can be found in the file  with the expected one
with the expected one 
 . Improving the accuracy
of the calculation is left as an exercise for the reader who has to control the
systematic errors of the calculations and achieve better accuracy in the
computation of
. Improving the accuracy
of the calculation is left as an exercise for the reader who has to control the
systematic errors of the calculations and achieve better accuracy in the
computation of  .
.
 , the trajectories of the logistic map
become non periodic and exhibit chaotic behavior. Chaotic behavior mostly
means sensitivity of the evolution of a dynamical system to the choice of initial
conditions. More precisely, it means that two different trajectories constructed
from infinitesimally close initial conditions, diverge very fast from each other. This
implies that there is a set of initial conditions that densely cover subintervals of
, the trajectories of the logistic map
become non periodic and exhibit chaotic behavior. Chaotic behavior mostly
means sensitivity of the evolution of a dynamical system to the choice of initial
conditions. More precisely, it means that two different trajectories constructed
from infinitesimally close initial conditions, diverge very fast from each other. This
implies that there is a set of initial conditions that densely cover subintervals of
 whose trajectories do not approach arbitrarily close to any cycle of finite
length.
whose trajectories do not approach arbitrarily close to any cycle of finite
length.
 ,
,  as initial points and
as initial points and
 . When the points
. When the points  ,
,  have a distance
have a distance  that for small enough
that for small enough  increases exponentially with
increases exponentially with  (the “time”),
i.e.
(the “time”),
i.e.

 is called a
is called a  is
is

 so that
so that
 . Then we obtain
. Then we obtain 
 and by
taking the logarithm and the limits we can prove (3.35) .
and by
taking the logarithm and the limits we can prove (3.35) . 







 is found at the fourth column
of the file
is found at the fourth column
of the file  ,
,  ,
,  and
and
 . The
. The  tend to lie on a straight line as
tend to lie on a straight line as  decreases. The slopes of these lines are
equal to the Liapunov exponent
decreases. The slopes of these lines are
equal to the Liapunov exponent  . Deviations from the straight line
behavior indicates corrections and systematic errors, as we point out in figure
. Deviations from the straight line
behavior indicates corrections and systematic errors, as we point out in figure
 , and the true value can be estimated as the average over several such
choices. We estimate the error of our computation from the standard
error of the mean. The reader should perform such a computation as an
exercise.
, and the true value can be estimated as the average over several such
choices. We estimate the error of our computation from the standard
error of the mean. The reader should perform such a computation as an
exercise.
 to the exponential function in
the following way: Since
to the exponential function in
the following way: Since 
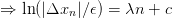 , we can
make a fit to a straight line instead. Using
, we can
make a fit to a straight line instead. Using  (
(







 . This equation is
approximately correct when (a) we have already reached the steady state and (b)
in the large
. This equation is
approximately correct when (a) we have already reached the steady state and (b)
in the large  limit. For this reason we should study if we obtain a satisfactory
convergence when we (a) “throw away” a number of
limit. For this reason we should study if we obtain a satisfactory
convergence when we (a) “throw away” a number of  (c) calculate the sum (
(c) calculate the sum ( . This has to be carefully repeated
for all values of
. This has to be carefully repeated
for all values of  since each factor will contribute differently to the
quality of the convergence: In regions that manifest chaotic behavior (large
since each factor will contribute differently to the
quality of the convergence: In regions that manifest chaotic behavior (large
 ) convergence will be slower. The program can be found in the file
) convergence will be slower. The program can be found in the file
 . At each step the sum divided by the number
of steps
. At each step the sum divided by the number
of steps  . This is a point where the system exhibits strong chaotic
behavior and convergence is achieved after we compute a large number
of steps. Using
. This is a point where the system exhibits strong chaotic
behavior and convergence is achieved after we compute a large number
of steps. Using  and
and  the achieved
accuracy is about
the achieved
accuracy is about  % with
% with  . The
main contribution to the error comes from the different paths followed by
each initial point chosen. The plot can be constructed with the
. The
main contribution to the error comes from the different paths followed by
each initial point chosen. The plot can be constructed with the  ,
,
 ,
,  and
and  and plots the
results from the contents of the file
and plots the
results from the contents of the file  on the value of
on the value of  . Using our experience
coming from the careful computation of
. Using our experience
coming from the careful computation of 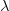 before, we will run the program for
several values of
before, we will run the program for
several values of  using the parameters
using the parameters  ,
,  from the initial point
from the initial point  . This calculation gives accuracy of the order of
. This calculation gives accuracy of the order of
 %. If we wish to measure
%. If we wish to measure  carefully and estimate the error of the results, we
have to follow the steps described in figures
carefully and estimate the error of the results, we
have to follow the steps described in figures  .
.















 correspond to stable
correspond to stable  -cycles. The intervals where
-cycles. The intervals where
 correspond to manifestation of
correspond to manifestation of  where the system exhibits
where the system exhibits  instead of an exponential, where
instead of an exponential, where  is
a positive exponent that needs to be determined. The parameter
is
a positive exponent that needs to be determined. The parameter  is
the one usually used in the literature. Strong chaos is obtained in the
is
the one usually used in the literature. Strong chaos is obtained in the
 limit. For larger
limit. For larger  , switching between chaotic and stable periodic
trajectories is observed each time
, switching between chaotic and stable periodic
trajectories is observed each time  changes sign. The critical values
of
changes sign. The critical values
of  can be computed with relatively high accuracy by restricting the
calculation to a small enough neighborhood of the critical point. You can do
this using the program listed above by setting the parameters
can be computed with relatively high accuracy by restricting the
calculation to a small enough neighborhood of the critical point. You can do
this using the program listed above by setting the parameters 









 of the values of
of the values of  in the interval
in the interval  .
After the transitional period, the distribution
.
After the transitional period, the distribution  for the
for the  cycles will have
support only at the points of the
cycles will have
support only at the points of the  cycles, whereas for the chaotic regimes it will
have support on subintervals of
cycles, whereas for the chaotic regimes it will
have support on subintervals of  . The distribution function
. The distribution function  is
independent for most of the initial points of the trajectories. If one obtains a large
number of points from many trajectories of the logistic map, it will be
practically impossible to understand that these are produced by a deterministic
rule. For this reason, chaotic systems can be used for the production of
is
independent for most of the initial points of the trajectories. If one obtains a large
number of points from many trajectories of the logistic map, it will be
practically impossible to understand that these are produced by a deterministic
rule. For this reason, chaotic systems can be used for the production of

 is the probability of observing the state
is the probability of observing the state  . In our case, we can make
an approximate calculation of
. In our case, we can make
an approximate calculation of  by dividing the interval
by dividing the interval  to
to  subintervals of width
subintervals of width  . For given
. For given  we obtain a large number
we obtain a large number  of values
of values
 of the logistic map and we compute the histogram
of the logistic map and we compute the histogram  of their distribution in
the intervals
of their distribution in
the intervals  . The probability density is obtained from the limit
of
. The probability density is obtained from the limit
of  as
as  becomes large and
becomes large and  small (large
small (large  ).
Indeed,
).
Indeed,  converges to
converges to  . We will define
. We will define
 .
.










 for chosen values of
for chosen values of  , and then the
entropy
, and then the
entropy  is calculated using (
is calculated using ( for the histograms. The probability density is
calculated in the array
for the histograms. The probability density is
calculated in the array 







 and the width
and the width  ,
so it should be large enough. The parameter
,
so it should be large enough. The parameter  and it should be large enough in
order to reduce the “noise” in
and it should be large enough in
order to reduce the “noise” in  . It is obvious that
. It is obvious that  becomes smaller. Appropriate choices lead to the plots
shown in figures
becomes smaller. Appropriate choices lead to the plots
shown in figures  ,
,  and
and  . We see that
stronger chaotic behavior means a wider distribution of the values of
. We see that
stronger chaotic behavior means a wider distribution of the values of
 .
.
 , which
increases even further as the chaotic behavior becomes stronger. During the
intermissions of the chaotic behavior there are sudden drops in the value of the
entropy. It is quite instructive to compare the entropy diagrams with the
corresponding bifurcation diagrams (see figure
, which
increases even further as the chaotic behavior becomes stronger. During the
intermissions of the chaotic behavior there are sudden drops in the value of the
entropy. It is quite instructive to compare the entropy diagrams with the
corresponding bifurcation diagrams (see figure  reaches its maximum value 4, but this is not done smoothly. By magnifying
the corresponding areas in the plot, we can see an infinite number of
sudden drops in the entropy in intervals of
reaches its maximum value 4, but this is not done smoothly. By magnifying
the corresponding areas in the plot, we can see an infinite number of
sudden drops in the entropy in intervals of  that become more and more
narrow.
that become more and more
narrow.
 are falling off
exponentially for large enough
are falling off
exponentially for large enough  .
.
 and plot the trajectories for
and plot the trajectories for  with
step
with
step  for
for  . Put the
. Put the  axis in a logarithmic
scale. From the resulting curves discuss whether you obtain an
exponential falloff.
axis in a logarithmic
scale. From the resulting curves discuss whether you obtain an
exponential falloff.
 for
for  to the function
to the function  and determine
the fitting parameters
and determine
the fitting parameters  and
and  . How do these parameters depend on
the initial point
. How do these parameters depend on
the initial point  ? You can use the following
? You can use the following  , therefore avoiding the transitional
period and the deviation from the exponential falloff for small
, therefore avoiding the transitional
period and the deviation from the exponential falloff for small
 .
.
 with step
with step  and for
and for  . As
you will be approaching
. As
you will be approaching  , you will need to discard more
points from near the origin. You might also need to increase
, you will need to discard more
points from near the origin. You might also need to increase
 for large
for large
 . Construct a table for the values of
. Construct a table for the values of  as a function of
as a function of
 .
. . How is this related to the
values that you computed in your table?
. How is this related to the
values that you computed in your table?
 . Choose
. Choose  and compare
your result to the known value
and compare
your result to the known value  . Repeat for
. Repeat for  for
for
 . What do you conclude about the point
. What do you conclude about the point
 ?
?
 . Calculate the stable
point
. Calculate the stable
point  and compare your result to the known value
and compare your result to the known value  .
How large should
.
How large should  . Take
. Take  and
and  by using the command
by using the command  . How big should
. How big should  and
and  with an accuracy of 6 significant
digits?
with an accuracy of 6 significant
digits?
 and
and  . Choose
. Choose  -
- and
and
 -
- .
.
 ,
,  ,
,  ,
,  for given
for given  on the same
graph. Use the commands:
on the same
graph. Use the commands:
 . Take
. Take  ,
,  ,
,  ,
,  ,
,
 . Determine the fixed points and the
. Determine the fixed points and the  -cycles from the intersections of
the plots with the diagonal
-cycles from the intersections of
the plots with the diagonal  .
.
 and
and  .
Repeat by dropping from the plot an increasing number of initial points, so
that in the end only the
.
Repeat by dropping from the plot an increasing number of initial points, so
that in the end only the  -cycles will remain. Do the same for
-cycles will remain. Do the same for
 .
.
 and for
and for  . Compute the first four bifurcation points with
an accuracy of 5 significant digits by magnifying the appropriate parts of the
plots. Take
. Compute the first four bifurcation points with
an accuracy of 5 significant digits by magnifying the appropriate parts of the
plots. Take  .
Compute graphically the bifurcation points
.
Compute graphically the bifurcation points  for
for 





 . Make sure that your results are stable against variations of the
parameters
. Make sure that your results are stable against variations of the
parameters  for
for  , and from the
dependence of your results on the choices of
, and from the
dependence of your results on the choices of  and compare your results to equation (
and compare your results to equation ( in equation (
in equation ( . Find the
roots obtained by the Newton-Raphson method when you choose
. Find the
roots obtained by the Newton-Raphson method when you choose




 .
What do you conclude concerning the basins of attraction of each root of the
polynomial? Make a plot of the polynomial in a neighborhood of its roots
and try other initial points that will converge to each one of the roots.
.
What do you conclude concerning the basins of attraction of each root of the
polynomial? Make a plot of the polynomial in a neighborhood of its roots
and try other initial points that will converge to each one of the roots.
 of the logistic map. Use appropriate areas of the bifurcation
diagram so that you can choose the initial points correctly. Check that
your result for
of the logistic map. Use appropriate areas of the bifurcation
diagram so that you can choose the initial points correctly. Check that
your result for  is the same for all
is the same for all  . Tune the parameters
chosen in your calculation on order to improve the accuracy of your
measurements.
. Tune the parameters
chosen in your calculation on order to improve the accuracy of your
measurements.
 and
and  .
.
 and
and  .
.
 for
for  of the logistic map
using the Newton-Raphson method. In order to achieve that, you should
determine the bifurcation points graphically in the bifurcation diagram first
and then choose the initial points in the Newton-Raphson method
appropriately. The program in
of the logistic map
using the Newton-Raphson method. In order to achieve that, you should
determine the bifurcation points graphically in the bifurcation diagram first
and then choose the initial points in the Newton-Raphson method
appropriately. The program in  . If these parameters are too small the
convergence will be unstable and if they are too large you will have large
systematic errors. Using this method, try to reproduce table
. If these parameters are too small the
convergence will be unstable and if they are too large you will have large
systematic errors. Using this method, try to reproduce table 






 of equation (
of equation ( and the critical value
and the critical value  by
assuming that for large enough
by
assuming that for large enough  ,
,  . This behavior
is a result of equation (
. This behavior
is a result of equation ( and
and  . This hypothesis is confirmed in
figure
. This hypothesis is confirmed in
figure  to
to  . Construct the same plot using the parameters of your
calculation.
. Construct the same plot using the parameters of your
calculation.




 . Choose one
bifurcation point of the 3-cycle, one of the 6-cycle and one of the 12-cycle
and magnify the bifurcation diagram in their neighborhood.
. Choose one
bifurcation point of the 3-cycle, one of the 6-cycle and one of the 12-cycle
and magnify the bifurcation diagram in their neighborhood.

 ,
,  ,
,  ,
,  for
for  ,
,
 ,
,  ,
, 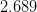 for
for  . For which values of
. For which values of  do you
expect to obtain stable
do you
expect to obtain stable  -cycles?
-cycles?
 plot the trajectories with initial points
plot the trajectories with initial points
 . For each
. For each  make a separate plot.
make a separate plot.
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
 . Determine
the point marking the onset of chaos as well as the point where
the 3-cycle starts. Magnify the diagram around a branch that you
will choose.
. Determine
the point marking the onset of chaos as well as the point where
the 3-cycle starts. Magnify the diagram around a branch that you
will choose.
 as in problem
as in problem  ? Is the value of
? Is the value of  the same as that of the logistic map?
the same as that of the logistic map?
 ,
,  ,
,  ,
,  ,
,  for
for
 ,
,  ,
,  ,
,  ,
,  . Which values of
. Which values of  are
expected to lead to stable
are
expected to lead to stable  -cycles?
-cycles?
 , plot the trajectories with initial points
, plot the trajectories with initial points
 . Make one plot for each
. Make one plot for each  .
.
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
 . Within which
limits do the values of
. Within which
limits do the values of  lie in? Repeat for
lie in? Repeat for  . What
do you observe? Determine the point marking the onset of chaos
as well as the point where the 3-cycle starts. Magnify the diagram
around a branch that you will choose.
. What
do you observe? Determine the point marking the onset of chaos
as well as the point where the 3-cycle starts. Magnify the diagram
around a branch that you will choose.
 . Within which
limits do the values of
. Within which
limits do the values of  lie in? Determine the point marking
the onset of chaos as well as the point where the 3-cycle starts.
Magnify the diagram around a branch that you will choose.
lie in? Determine the point marking
the onset of chaos as well as the point where the 3-cycle starts.
Magnify the diagram around a branch that you will choose.
 for
for  as well as the first two bifurcation points of
the 3-cycle.
as well as the first two bifurcation points of
the 3-cycle.
 . Within which limits do
the values of
. Within which limits do
the values of  lie in? On the same graph, plot the functions
lie in? On the same graph, plot the functions  ,
,
 .
.
 and
and  .
At which point do the two disconnected intervals within which
.
At which point do the two disconnected intervals within which  take their values merge into one? Magnify the areas
take their values merge into one? Magnify the areas  ,
,
 and
and  ,
,  and determine the merging points of two disconnected intervals within
which
and determine the merging points of two disconnected intervals within
which  take their values.
take their values.

 and
and 

 . Make your program to take as the initial point of the new
trajectory to be the last one of the previous trajectory and choose
. Make your program to take as the initial point of the new
trajectory to be the last one of the previous trajectory and choose
 for
for  . Repeat for
. Repeat for  . What do you
observe? Note that as
. What do you
observe? Note that as  is increased, we obtain bifurcations and
“anti-bifurcations”.
is increased, we obtain bifurcations and
“anti-bifurcations”.
![xn+1 = [xn + r − q sin(2πxn )] mod1.](main_latex1416x.png)
 so that
so that  ).
Construct the bifurcation diagram for
).
Construct the bifurcation diagram for  and
and  .
.
 that originally are at a
distance
that originally are at a
distance  . Choose
. Choose 





 and calculate the Liapunov exponent by fitting
to a straight line appropriately. Compute the mean value and the standard
error of the mean.
and calculate the Liapunov exponent by fitting
to a straight line appropriately. Compute the mean value and the standard
error of the mean.




 for the logistic map. Use both ways mentioned in the text. Choose at least 5
different initial points and calculate the mean and the standard error of the
mean of your results. Compare the values of
for the logistic map. Use both ways mentioned in the text. Choose at least 5
different initial points and calculate the mean and the standard error of the
mean of your results. Compare the values of  that you obtain with each
method and comment.
that you obtain with each
method and comment.
 numerically as the limit
numerically as the limit  for the
logistic map with an accuracy of nine significant digits. Use the
calculation of the Liapunov exponent
for the
logistic map with an accuracy of nine significant digits. Use the
calculation of the Liapunov exponent  given by equation (
given by equation ( of the logistic map numerically for which
we (a) enter a stable 3-cycle (b) reenter into the chaotic behavior.
Do the calculation by computing the Liapunov exponent
of the logistic map numerically for which
we (a) enter a stable 3-cycle (b) reenter into the chaotic behavior.
Do the calculation by computing the Liapunov exponent  and
compare your results with the ones obtained from the bifurcation
diagram.
and
compare your results with the ones obtained from the bifurcation
diagram.
![r(1−xn)
xn+1 = xne , 1.8 < r < 4
xn+1 = r sin (πxn), 0.6 < r < 1
2
xn+1 = 1 − rx n, 0 < r < 2
xn+1 = e− rx2n + q, r = 7.5,− 1 < q < 1
[ ]
xn+1 = xn + 1-− q sin(2πxn ) mod1, 0 < q < 2, (3.44)
3](main_latex1441x.png)
 for the Gauss
map (
for the Gauss
map (
 ) and observe the differences. For the circle map
(
) and observe the differences. For the circle map
(
![[xn + 1 ∕3 − qsin(2πxn )] mod1](main_latex1446x.png) ) study carefully the values
) study carefully the values
 .
.
 for
for  ,
,  ,
,  and
and  . Determine the points where
you have stronger chaos by observing
. Determine the points where
you have stronger chaos by observing  and the corresponding values of
the entropy. Compute the entropy for
and the corresponding values of
the entropy. Compute the entropy for  by taking
by taking
 where we enter to and exit from
chaos. Compare your results with the computation of the Liapunov
exponent.
where we enter to and exit from
chaos. Compare your results with the computation of the Liapunov
exponent.

 and
and  for
for
 ,
, 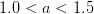 . Check if the values
. Check if the values  that
we will use below correspond to stable periodic trajectories or
chaotic behavior.
that
we will use below correspond to stable periodic trajectories or
chaotic behavior.




 ,
,  .
Each of the points
.
Each of the points  will evolve according to equation
(
will evolve according to equation
(
 to the
to the  ,
,
 ,
,  .
.
 ,
,  and plot the points
and plot the points  for
for









 on the same
diagram.
on the same
diagram.
 ,
,  and plot the points
and plot the points  for
for
 on the same diagram.
on the same diagram.
 ,
,  and plot the points
and plot the points  for
for
 on the same diagram. Observe the Hénon strange
attractor and its fractal properties. It is characterized by a
Hausdorff
on the same diagram. Observe the Hénon strange
attractor and its fractal properties. It is characterized by a
Hausdorff . Then magnify the regions
. Then magnify the regions


 and
and  for
for
 ,
,  . Choose four different initial conditions
. Choose four different initial conditions

 . What do you observe?
. What do you observe?
 ,
,  .
.
 ,
, 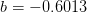 ,
,  ,
,  . Plot a
trajectory on the plane by plotting the points
. Plot a
trajectory on the plane by plotting the points  for
for
 with
with  .
.
 ,
,  ,
,  ,
,  given above. Choose
given above. Choose  ,
,  ,
,
 ,
,  ,
,  .
.
 .
.


 . The equations (
. The equations (


 in a homogeneous gravitational field
in a homogeneous gravitational field  (figure
(figure 






















![[ti,tf]](main_latex1549x.png) to
to  equal
intervals
equal
intervals , where
, where  . The derivatives are
approximated by the relations
. The derivatives are
approximated by the relations  , so that
, so that 
 is the angular acceleration. This is the so-called
is the angular acceleration. This is the so-called
 .
This is most easily seen by Taylor expanding around the point
.
This is most easily seen by Taylor expanding around the point  and neglecting all terms starting from the second derivative and
beyond
and neglecting all terms starting from the second derivative and
beyond ! We expect that errors accumulate in an
additive way at each integration step, and since the number of steps is
! We expect that errors accumulate in an
additive way at each integration step, and since the number of steps is
 the total error should be
the total error should be  . This is indeed
what happens, and we say that Euler’s method is a first order method. Its range
of applicability is limited and we only study it for academic reasons. Euler’s
method is
. This is indeed
what happens, and we say that Euler’s method is a first order method. Its range
of applicability is limited and we only study it for academic reasons. Euler’s
method is  . It can be put in a more balanced form by using
the velocity
. It can be put in a more balanced form by using
the velocity  . This way we obtain the
Euler-Cromer method with a slightly improved behavior, but which is still of first
order
. This way we obtain the
Euler-Cromer method with a slightly improved behavior, but which is still of first
order 
 . This is given by the equations
. This is given by the equations 
 . We make one Euler time step
. We make one Euler time step  . If the initial conditions are
. If the initial conditions are  ,
,  , then we
, then we

 ,
otherwise it will spoil and eventually dominate the
,
otherwise it will spoil and eventually dominate the  total error of the
method introduced by the intermediate steps. At the last step we also have to
take
total error of the
method introduced by the intermediate steps. At the last step we also have to
take

 due to roundoff errors. In particular, the
second equation in (
due to roundoff errors. In particular, the
second equation in ( , this difference has to be
computed from the last digits of the finite representation of the numbers
, this difference has to be
computed from the last digits of the finite representation of the numbers  and
and  in the computer memory. The accuracy in the determination of
in the computer memory. The accuracy in the determination of
 decreases until it eventually becomes
decreases until it eventually becomes  is smaller by a factor
is smaller by a factor  compared to the
term
compared to the
term  in Euler’s method. At some point, by decreasing
in Euler’s method. At some point, by decreasing  , we obtain
, we obtain
 and the accuracy of the method vanishes due to the finite
representation of real number in the memory of the computer. When the
numbers
and the accuracy of the method vanishes due to the finite
representation of real number in the memory of the computer. When the
numbers  and
and  differ from each other by more that
approximately seven orders of magnitude, adding the first one to the
second is equivalent to adding zero and the contribution of the acceleration
vanishes
differ from each other by more that
approximately seven orders of magnitude, adding the first one to the
second is equivalent to adding zero and the contribution of the acceleration
vanishes . For
starters we take
. For
starters we take  , the angles
, the angles  and the angular velocities
and the angular velocities  for
for
 . The user determines the time interval for the integration from
. The user determines the time interval for the integration from
 to
to  and the number of discrete times
and the number of discrete times  and
and  . After this, we call the main integration routines which
take as input the initial conditions, the time interval of the integration and the
number of discrete times
. After this, we call the main integration routines which
take as input the initial conditions, the time interval of the integration and the
number of discrete times  , the integration in each of the subroutines is performed
in do loops which advance the solution for time
, the integration in each of the subroutines is performed
in do loops which advance the solution for time  . The results are stored at
each step in the arrays
. The results are stored at
each step in the arrays  . The
Euler–Verlet method converges much faster, but roundoff errors kick in soon. This
is more obvious in figure
. The
Euler–Verlet method converges much faster, but roundoff errors kick in soon. This
is more obvious in figure  ):
): 
 where the methods converge. This way we can check our program
for bugs. The plot of the functions above can be done with the following
where the methods converge. This way we can check our program
for bugs. The plot of the functions above can be done with the following  axis and the value found in the second column
minus the value of the function
axis and the value found in the second column
minus the value of the function  equal to the value found in
the first column on the
equal to the value found in
the first column on the  axis. This way, we can make the plots shown
in
axis. This way, we can make the plots shown
in![[ti,tf]](main_latex1610x.png) by
by  discrete times is of order
discrete times is of order  , where
, where
 is the time step of the integration. In this section we will
discuss a generalization of this approach where the total error will be of higher
order in
is the time step of the integration. In this section we will
discuss a generalization of this approach where the total error will be of higher
order in  . This is the class of Runge-Kutta methods which are one step
algorithms where the total discretization error is of order
. This is the class of Runge-Kutta methods which are one step
algorithms where the total discretization error is of order  . The
local error introduced at each step is of order
. The
local error introduced at each step is of order  leading after
leading after
 steps to a maximum error of order
steps to a maximum error of order

 order.
The
order.
The .
.
 which evolves in time according to the differential equation:
which evolves in time according to the differential equation:




 , therefore the
error after integrating from
, therefore the
error after integrating from  is
is  . Indeed,
. Indeed,

 we
determine the point
we
determine the point  .
.

 by making a linear extrapolation from
by making a linear extrapolation from
 in the direction of the derivative
in the direction of the derivative  . Then we use the
slope at point 2 as an
. Then we use the
slope at point 2 as an  . We use
. We use  to linearly
extrapolate from
to linearly
extrapolate from  to
to  . Summarizing, we have that
. Summarizing, we have that 
 twice at each step,
thereby doubling the computational effort. The error at each step (4.19) becomes
twice at each step,
thereby doubling the computational effort. The error at each step (4.19) becomes
 , however, giving a total error of
, however, giving a total error of  . So for given
computational time, (4.19) is superior to (4.17) .
. So for given
computational time, (4.19) is superior to (4.17) .

 per step, but the
total error becomes now
per step, but the
total error becomes now  and the method is superior to that of (
and the method is superior to that of ( to
to  . Point 2 is
determined by linearly extrapolating from
. Point 2 is
determined by linearly extrapolating from  to the midpoint of the
interval
to the midpoint of the
interval  by using the direction given by the derivative
by using the direction given by the derivative
 , i.e.
, i.e.  . We calculate the derivative
. We calculate the derivative
 at the point 2 and we use it in order to determine
point 3, also located at the midpoint of the interval
at the point 2 and we use it in order to determine
point 3, also located at the midpoint of the interval  . Then we calculate
the derivative
. Then we calculate
the derivative  at the point 3 and we use
it to linearly extrapolate to the
at the point 3 and we use
it to linearly extrapolate to the  , thereby
obtaining point 4, i.e.
, thereby
obtaining point 4, i.e.  . Then we calculate the derivative
. Then we calculate the derivative
 at the point 4, and we use all four derivative
at the point 4, and we use all four derivative  and
and  as estimators of the derivative of the function in the interval
as estimators of the derivative of the function in the interval
 . If each derivative contributes with a particular weight in this
estimate, the discretization error can become
. If each derivative contributes with a particular weight in this
estimate, the discretization error can become  . Such a choice is
. Such a choice is

 ,
,  ,
,  and
and  respectively. A generic small
change in these values will increase the discretization error to worse than
respectively. A generic small
change in these values will increase the discretization error to worse than
 .
.
 the discretization
errors decrease, but that roundoff errors will start showing up for small enough
the discretization
errors decrease, but that roundoff errors will start showing up for small enough
 . Therefore, a careful determination of
. Therefore, a careful determination of  that minimizes the total error
should be made by studying the dependence of the results as a function of
that minimizes the total error
should be made by studying the dependence of the results as a function of
 .
.
 and
and  so
that
so
that






 and the corresponding values of the functions
and the corresponding values of the functions  and
and  ,
,  . The main program calls the driver routine
. The main program calls the driver routine























 . We will take
. We will take  (
( ). Therefore the relevant part of the program in
). Therefore the relevant part of the program in  to
to  with the
initial conditions
with the
initial conditions  ,
,  . The time step
. The time step  is varied by
varying the number of steps
is varied by
varying the number of steps 
 and
and  as a
function of the time step
as a
function of the time step  . The results are shown in figures 4.11–4.14. We
note that for the Euler method and the Euler–Cromer method, the errors
are of order
. The results are shown in figures 4.11–4.14. We
note that for the Euler method and the Euler–Cromer method, the errors
are of order  as expected. However, the latter has smaller errors
compared to the first one. For the Euler–Verlet method, the error turns out
to be of order
as expected. However, the latter has smaller errors
compared to the first one. For the Euler–Verlet method, the error turns out
to be of order  whereas for the 4th order Runge–Kutta is of
order
whereas for the 4th order Runge–Kutta is of
order .
.

 is shown in figures
is shown in figures

 and
and  is the angular frequency of the driving
force.
is the angular frequency of the driving
force.
 . The real solutions of the differential
equation
. The real solutions of the differential
equation are given by
are given by



 case, the general solution is obtained from the sum of a special
solution
case, the general solution is obtained from the sum of a special
solution  and the solution of the homogeneous equation
and the solution of the homogeneous equation  . A special
solution can be obtained from the ansatz
. A special
solution can be obtained from the ansatz  ,
which when substituted in (
,
which when substituted in ( and
and  we find
that
we find
that
![a0 [(ω20 − ω2 )cosωt + γ ωsin ωt]
xs(t) = ---------2----2-2----2-2-------,
(ω 0 − ω ) + ω γ](main_latex1734x.png)

 decreases exponentially with time and eventually only
decreases exponentially with time and eventually only
 remains. The only case where this is not true, is when we have
resonance without damping for
remains. The only case where this is not true, is when we have
resonance without damping for  ,
,  . In that case the solution
is
. In that case the solution
is

 ,
,  ,
,
 ,
,  are entered interactively by the user from the standard input
are entered interactively by the user from the standard input 
















 to an oscillating motion with damping
amplitude for
to an oscillating motion with damping
amplitude for  . The exponential decrease of the amplitude is shown in
figure
. The exponential decrease of the amplitude is shown in
figure  from the damping coefficient
from the damping coefficient
 is shown in figure
is shown in figure 
 . The period
. The period  can be estimated from the
time between two consecutive extrema of
can be estimated from the
time between two consecutive extrema of  or two consecutive zeros of the
velocity
or two consecutive zeros of the
velocity  (see figure
(see figure  to the point
to the point  , independently of the
initial conditions. Such a point is an example of a system’s
, independently of the
initial conditions. Such a point is an example of a system’s 













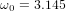





 becomes dominant when
the exponentials have damped away.
becomes dominant when
the exponentials have damped away.  can be written in the form
can be written in the form

 on the angular frequency of the driving force. Finally we study
the trajectory of the system in phase space. As we can see in figure 4.20, this time
the attractor is an ellipse, which is a one dimensional curve instead of a zero
dimensional point. For large enough times, all trajectories approach their
attractor asymptotically.
on the angular frequency of the driving force. Finally we study
the trajectory of the system in phase space. As we can see in figure 4.20, this time
the attractor is an ellipse, which is a one dimensional curve instead of a zero
dimensional point. For large enough times, all trajectories approach their
attractor asymptotically.

 is the angle of the pendulum with the vertical axis,
is the angle of the pendulum with the vertical axis,  is the damping coefficient,
is the damping coefficient,  is the pendulum’s natural angular
frequency,
is the pendulum’s natural angular
frequency,  is the angular frequency of the driving force and
is the angular frequency of the driving force and  is
the amplitude of the external angular acceleration caused by the driving
force.
is
the amplitude of the external angular acceleration caused by the driving
force.
 , which is an attractor for the system. This continues
to happen for small enough
, which is an attractor for the system. This continues
to happen for small enough  , but for
, but for  the behavior of the system
becomes more complicated.
the behavior of the system
becomes more complicated.
 ,
,  ,
,  . The final program can be found in the file
. The final program can be found in the file ![[− π,π]](main_latex1801x.png) .
.
 ,
,  , and
, and
 unless we explicitly state otherwise. The natural period of the pendulum
is
unless we explicitly state otherwise. The natural period of the pendulum
is  whereas that of the driving force is
whereas that of the driving force is
 . For
. For  , with
, with  , the
point
, the
point  is an attractor, which means that the pendulum eventually
stops at its stable equilibrium point. For
is an attractor, which means that the pendulum eventually
stops at its stable equilibrium point. For  the attractor is a
closed curve, which means that the pendulum at its steady state oscillates
indefinitely without circling through its unstable equilibrium point at
the attractor is a
closed curve, which means that the pendulum at its steady state oscillates
indefinitely without circling through its unstable equilibrium point at  .
The period of motion is found to be twice that of the driving force. For
.
The period of motion is found to be twice that of the driving force. For
 the attractor is an open curve, because at its steady state the
pendulum crosses the
the attractor is an open curve, because at its steady state the
pendulum crosses the  point. The period of the motion becomes
equal to that of the driving force. For
point. The period of the motion becomes
equal to that of the driving force. For  we have
we have  , but the trajectory is still periodic. For
even larger values of
, but the trajectory is still periodic. For
even larger values of the system enters into a chaotic regime where
the trajectories are non periodic. For
the system enters into a chaotic regime where
the trajectories are non periodic. For  we find the system in a
periodic steady state again, whereas for
we find the system in a
periodic steady state again, whereas for  –
–  we have period
doubling. For
we have period
doubling. For  we enter into a chaotic regime again etc. These
results can be seen in figures
we enter into a chaotic regime again etc. These
results can be seen in figures 





























 –multiple of the period of
the driving force then the Poincaré diagram consists of only
–multiple of the period of
the driving force then the Poincaré diagram consists of only  points.
Therefore, in the period doubling regime, the points of the Poincaré diagram
double at each period doubling point. In the chaotic regime, the Poincaré
diagram consists of an infinite number of points which belong to sets that
have interesting fractal structure. One way to construct the Poincaré
diagram numerically, is to process the data of the output file
points.
Therefore, in the period doubling regime, the points of the Poincaré diagram
double at each period doubling point. In the chaotic regime, the Poincaré
diagram consists of an infinite number of points which belong to sets that
have interesting fractal structure. One way to construct the Poincaré
diagram numerically, is to process the data of the output file  ,
the number of points of time and the final time
,
the number of points of time and the final time  . We calculate
the period
. We calculate
the period  in the regime where the pendulum at its steady
state has a circular trajectory with a positive or negative direction. By
taking a large sample of initial conditions and recording the direction of
the resulting motion after the transient behavior, we obtain figure
in the regime where the pendulum at its steady
state has a circular trajectory with a positive or negative direction. By
taking a large sample of initial conditions and recording the direction of
the resulting motion after the transient behavior, we obtain figure 









 integration steps. In this method, these errors must be
studied carefully:
integration steps. In this method, these errors must be
studied carefully:  does not accumulate because it is given
by the
does not accumulate because it is given
by the  .
.
 is the
is the  to
to  . Then according to the expansions
(
. Then according to the expansions
( .
Then
.
Then


 , we obtain
, we obtain


 .
.

 which should depend only on the
position
which should depend only on the
position  and not on the velocity.
and not on the velocity.
 . This choice is special, since
by choosing another point (e.g.
. This choice is special, since
by choosing another point (e.g.  ) the result would have not been the
same. Indeed, from the relation
) the result would have not been the
same. Indeed, from the relation
 we obtain
we obtain


 term it is necessary to place the
intermediate point at time
term it is necessary to place the
intermediate point at time  .
.
 we obtain
we obtain

 ,
,  etc. We define
etc. We define 
 of the last
equation in the error are identical with those of equation (4.43) . By expanding
of the last
equation in the error are identical with those of equation (4.43) . By expanding
 we obtain
we obtain 


 ,
,  ,
,  leads to equation (4.19) . Some other
choices in the bibliography are
leads to equation (4.19) . Some other
choices in the bibliography are  and
and  .
.
 .
.

 ,
,  ,
,  .
.
 on the particle. Consider the
case
on the particle. Consider the
case  ,
,  ,
, 
 . Calculate the
limiting velocity of the particle numerically and compare the value
obtained to the theoretical expectation.
. Calculate the
limiting velocity of the particle numerically and compare the value
obtained to the theoretical expectation.
 .
.
 ,
,  and calculate its mechanical energy as a
function of time. Is it monotonic? Why? (show that
and calculate its mechanical energy as a
function of time. Is it monotonic? Why? (show that  ).
Repeat for
).
Repeat for  . When is the system oscillating and when it’s
not? Calculate numerically the critical value of
. When is the system oscillating and when it’s
not? Calculate numerically the critical value of  for which the system
passes from a non oscillating to an oscillating regime. Compare your results
with the theoretical expectations.
for which the system
passes from a non oscillating to an oscillating regime. Compare your results
with the theoretical expectations.
 numerically and compare with equation (
numerically and compare with equation ( . Define “momentary” to be an impulse given by the
acceleration
. Define “momentary” to be an impulse given by the
acceleration  by an appropriately small time interval
by an appropriately small time interval  . The
acceleration is
. The
acceleration is  for all other times. Calculate the amplitude
for all other times. Calculate the amplitude  for
for
 and
and  .
.

 and
and  . Calculate
the amplitude
. Calculate
the amplitude  .
.

 and
and  . Calculate
the amplitude
. Calculate
the amplitude  . Compare your results with those of the previous
problem and comment about.
. Compare your results with those of the previous
problem and comment about.
 identical, independent harmonic
oscillators. Take
identical, independent harmonic
oscillators. Take  and choose random initial conditions for each one
of them. Study their trajectories in phase space and check whether they
cross each other. Comment on your results.
and choose random initial conditions for each one
of them. Study their trajectories in phase space and check whether they
cross each other. Comment on your results.
 harmonic oscillators of the previous problem in a
small square in phase space whose center is at the origin of the
axes. Consider the evolution of the system in time. Does the shape
of the rectangle change in time? Does the area change in time?
Explain...
harmonic oscillators of the previous problem in a
small square in phase space whose center is at the origin of the
axes. Consider the evolution of the system in time. Does the shape
of the rectangle change in time? Does the area change in time?
Explain...
 .
Take
.
Take  .
.
 ,
,  ,
,  .
Study the transient behavior of the system in the plots of
.
Study the transient behavior of the system in the plots of  ,
,  for
for
 .
.
 ,
,  ,
,  and study the phase space trajectories for
and study the phase space trajectories for  0.1, 0.19, 0.21, 0.25, 0.5,
0.71, 0.79, 0.85, 1.02, 1.031, 1.033, 1.05, 1.08, 1.1, 1.4, 1.8, 3.1, 3.5, 3.8, 4.2,
4.42, 4.44, 4.445, 4.447, 4.4488. Consider both the transient behavior and
the steady state motion.
0.1, 0.19, 0.21, 0.25, 0.5,
0.71, 0.79, 0.85, 1.02, 1.031, 1.033, 1.05, 1.08, 1.1, 1.4, 1.8, 3.1, 3.5, 3.8, 4.2,
4.42, 4.44, 4.445, 4.447, 4.4488. Consider both the transient behavior and
the steady state motion.

 ,
,
 and
and  is periodic. Measure the period of the
motion with an accuracy of three significant digits and compare it
with the natural period of the pendulum and with the period of the
driving force. Take as initial conditions the following pairs:
is periodic. Measure the period of the
motion with an accuracy of three significant digits and compare it
with the natural period of the pendulum and with the period of the
driving force. Take as initial conditions the following pairs: 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  . Check if the period is independent of the initial
conditions.
. Check if the period is independent of the initial
conditions.

 takes values in
the interval
takes values in
the interval ![[0.2,5.0]](main_latex1956x.png) . Consider specific discrete values of
. Consider specific discrete values of  by splitting
the interval above in subintervals of width equal to
by splitting
the interval above in subintervals of width equal to  .
For each value of
.
For each value of  , record in a file the value of
, record in a file the value of  , the angular
position and the angular velocity of the pendulum when
, the angular
position and the angular velocity of the pendulum when  with
with
 :
:

 is made so that the transient behavior will be
discarded and study only the steady state of the pendulum. You
may take
is made so that the transient behavior will be
discarded and study only the steady state of the pendulum. You
may take  ,
,  ,
,  ,
,  , and
split the intervals
, and
split the intervals ![[tk,tk + π]](main_latex1969x.png) to 50 subintervals. Choose
to 50 subintervals. Choose  ,
,
 .
.
 .
.
 .
.
 ,
,  .
Repeat your analysis for
.
Repeat your analysis for  ,
,  .
.
![A ∈ [1.0000,1.0400]](main_latex1978x.png) with
with
 and
and ![A ∈ [4.4300,4.4500]](main_latex1980x.png) with
with  and
compute with the given accuracy the value
and
compute with the given accuracy the value  where the system
enters into the chaotic behavior regime.
where the system
enters into the chaotic behavior regime.
 for
for 




 . Put 2000 points for each value of
. Put 2000 points for each value of  and
commend on the strength of the chaotic behavior of the pendulum.
and
commend on the strength of the chaotic behavior of the pendulum.
 etc.
etc.
 ,
,  ,
,  ,
,  , and the values of the functions of
time will be stored in the arrays
, and the values of the functions of
time will be stored in the arrays  ,
,  ,
,  ,
,  . The integration is performed by a call to the
subroutine
. The integration is performed by a call to the
subroutine
 so that
so that


 is the direction of the initial velocity and
is the direction of the initial velocity and  is the
maximum height of the trajectory.
is the
maximum height of the trajectory. 














 (
(

 , the coordinate
, the coordinate  etc. The keyword
etc. The keyword  ,
,
 ) and the scattering of a particle in a Coulomb field –
try them! I hope that you will have enough curiosity to look “under the
hood” of the scripts and try to modify them or create new ones. Some
advise to the lazy guys: If you need to program your own force field follow
the recipe: Write the code of your acceleration field in a file named e.g.
) and the scattering of a particle in a Coulomb field –
try them! I hope that you will have enough curiosity to look “under the
hood” of the scripts and try to modify them or create new ones. Some
advise to the lazy guys: If you need to program your own force field follow
the recipe: Write the code of your acceleration field in a file named e.g.
 , therefore
, therefore 

 (
( const.,
const.,  ).
).
 ,
,  )
)  is shown in figure
is shown in figure 







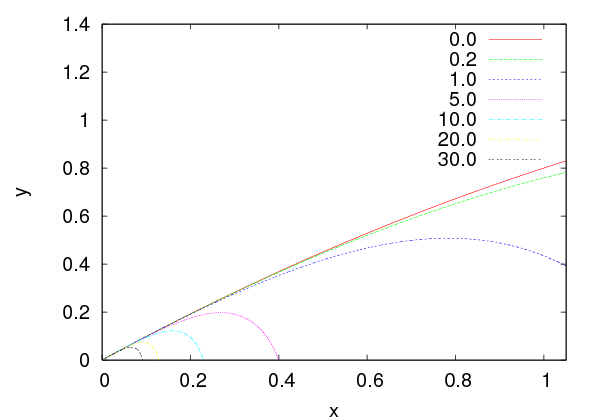





 and a planet “earth”
at distance
and a planet “earth”
at distance  from the sun and mass
from the sun and mass  such that
such that  . According to
Newton’s law of gravity, the earth’s acceleration is
. According to
Newton’s law of gravity, the earth’s acceleration is
 ,
,  ,
,  .
When the hypothesis
.
When the hypothesis  is not valid, the two body problem is reduced to
that of the one body problem with the mass replaced by the reduced mass
is not valid, the two body problem is reduced to
that of the one body problem with the mass replaced by the reduced mass


 with respect to the center of the force, which in turn
implies that the motion is confined on one plane. We choose the
with respect to the center of the force, which in turn
implies that the motion is confined on one plane. We choose the  axis so
that
axis so
that



 . This is a system of two coupled differential equations for the
functions
. This is a system of two coupled differential equations for the
functions  ,
,  . The trajectories are conic sections which are either an
ellipse (bound states - “planet”), a parabola (e.g. escape to infinity when the
particle starts moving with speed equal to the escape velocity) or a hyperbola
(e.g. scattering).
. The trajectories are conic sections which are either an
ellipse (bound states - “planet”), a parabola (e.g. escape to infinity when the
particle starts moving with speed equal to the escape velocity) or a hyperbola
(e.g. scattering).
 of a
planet satisfies the equation
of a
planet satisfies the equation

 is the semi-major axis of the elliptical trajectory. The eccentricity is a
measure of the deviation of the trajectory from being circular
is the semi-major axis of the elliptical trajectory. The eccentricity is a
measure of the deviation of the trajectory from being circular
 is the semi-minor axis. The eccentricity is 0 for the circle and tends to 1
as the ellipse becomes more and more elongated. The foci
is the semi-minor axis. The eccentricity is 0 for the circle and tends to 1
as the ellipse becomes more and more elongated. The foci  and
and  are
located at a distance
are
located at a distance  from the center of the
from the center of the
 and take special care to avoid hitting the center of the
force, the singular point at
and take special care to avoid hitting the center of the
force, the singular point at  . The same code can be used for the
electrostatic Coulomb field with
. The same code can be used for the
electrostatic Coulomb field with  .
.
 ,
,
 ,
,  ,
,  and vary
and vary  . We measure the period
. We measure the period  and
the length of the semi axes of the resulting ellipse. The results can be found in
table
and
the length of the semi axes of the resulting ellipse. The results can be found in
table 

















 lie on a straight line. Using a linear least
squares fit we calculate the slope and the intercept which should be equal to
lie on a straight line. Using a linear least
squares fit we calculate the slope and the intercept which should be equal to  and
and  respectively. This is left as an exercise.
respectively. This is left as an exercise.
 , the particle escapes from the influence of the gravitational
field to infinity. The escape velocity corresponds to zero mechanical energy, which
gives
, the particle escapes from the influence of the gravitational
field to infinity. The escape velocity corresponds to zero mechanical energy, which
gives

 ,
,  ,
,  , we obtain
, we obtain 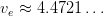 . The
numerical calculation of
. The
numerical calculation of  is left as an exercise.
is left as an exercise. 

 . Scattering problems are interesting because we can
infer to the properties of the scattering potential from the distribution of
the scattering angle. This approach is heavily used in today’s particle
accelerators for the study of fundamental interactions between elementary
particles.
. Scattering problems are interesting because we can
infer to the properties of the scattering potential from the distribution of
the scattering angle. This approach is heavily used in today’s particle
accelerators for the study of fundamental interactions between elementary
particles. by other hard spheres or radius
by other hard spheres or radius  . The interaction
potential
. The interaction
potential
 is the distance between the center of
is the distance between the center of  from the center of
from the center of  .
.



 be the intensity of the
beam
be the intensity of the
beam its cross sectional area. Assume that the target has
its cross sectional area. Assume that the target has  particles per unit
area. The cross sectional area of the interaction is
particles per unit
area. The cross sectional area of the interaction is  where
where  and
and  are the radii of the scattered particles and targets respectively (see figure
(
are the radii of the scattered particles and targets respectively (see figure
(
 is the total number of target spheres which lie within the beam. On
the average, the scattering rate is
is the total number of target spheres which lie within the beam. On
the average, the scattering rate is 
 of the interaction. The differential cross section
of the interaction. The differential cross section  is defined by the
relation
is defined by the
relation
 is the number of particles per unit time scattered within the solid
angle
is the number of particles per unit time scattered within the solid
angle  .
. 




 and
and
 . This is the relation that we will use in the numerical calculation of
. This is the relation that we will use in the numerical calculation of
 .
.
 depends on the
impact parameter
depends on the
impact parameter  .
. , thickness
, thickness  and area
and area  is scattered in angles between
is scattered in angles between  and
and  . Since there is only one particle at the target we have that
. Since there is only one particle at the target we have that
 . The number of particles per unit time crossing the ring is
. The number of particles per unit time crossing the ring is  ,
therefore
,
therefore

 sign is because as
sign is because as  increases,
increases,  decreases). From the potential we can
calculate
decreases). From the potential we can
calculate  and from
and from  we can calculate
we can calculate  . Conversely, if we measure
. Conversely, if we measure
 , we can calculate
, we can calculate  .
.
 (“electron”) in a
Coulomb potential of a much heavier charge
(“electron”) in a
Coulomb potential of a much heavier charge  (“nucleus”) is called
Rutherford scattering. In this case, the interaction potential is given by
(“nucleus”) is called
Rutherford scattering. In this case, the interaction potential is given by


 and the magnitude of its angular
momentum is
and the magnitude of its angular
momentum is  , where
, where  . The dependence of the impact parameter
on the scattering angle is
. The dependence of the impact parameter
on the scattering angle is 


















 where the scattering angle is
where the scattering angle is  . A large number of integration steps
is needed in order to obtain the desired accuracy. A useful monitor of
the accuracy of the calculation is the measurement of the energy of the
particle which should be conserved. The results are shown in table
. A large number of integration steps
is needed in order to obtain the desired accuracy. A useful monitor of
the accuracy of the calculation is the measurement of the energy of the
particle which should be conserved. The results are shown in table 




































































































































































 and
and  . For this reason we split the interval
. For this reason we split the interval ![[0,π ]](main_latex2345x.png) in
in  bins
so that
bins
so that  . We perform “scattering experiments” by varying
. We perform “scattering experiments” by varying
![b ∈ [bm,bM ]](main_latex2348x.png) with step
with step  . Due to the symmetry of the problem we fix
. Due to the symmetry of the problem we fix  to be a constant, therefore a given
to be a constant, therefore a given  corresponds to a cone with an
opening angle
corresponds to a cone with an
opening angle  and an apex at the center of scattering. For given
and an apex at the center of scattering. For given  we
measure the scattering angle
we
measure the scattering angle  and record the number of particles per unit
time
and record the number of particles per unit
time  . The latter is proportional to the area of the ring of
radius
. The latter is proportional to the area of the ring of
radius  . All we need now is the beam intensity
. All we need now is the beam intensity  which is the total
number of particles per unit time
which is the total
number of particles per unit time  (note than in the ratio
(note than in the ratio
 the proportionality constant and
the proportionality constant and  cancel) and the solid angle
cancel) and the solid angle
 . Finally we can easily use equation (
. Finally we can easily use equation ( . The program that performs this calculation is in
the file
. The program that performs this calculation is in
the file 
 by the
hydrogen atom. The positron has positive charge
by the
hydrogen atom. The positron has positive charge  and the hydrogen atom
consists of a positively charged proton with charge
and the hydrogen atom
consists of a positively charged proton with charge  in an electron
cloud of opposite charge
in an electron
cloud of opposite charge  . We set the scales so that
. We set the scales so that  and
and
 . We will perform a numerical calculation of
. We will perform a numerical calculation of  ,
,  and
and
 .
.

 for
for  . The program containing the calculation of the
acceleration caused by this force can be found in the file
. The program containing the calculation of the
acceleration caused by this force can be found in the file  (see
problem 5.
(see
problem 5.





































 and the equations of motion become (
and the equations of motion become ( )
)

 . The total energy of the system is
. The total energy of the system is

 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,  and
and  .
.
 and compute its trajectory for
and compute its trajectory for
 . Set
. Set  and calculate the
resulting radius of the trajectory. Plot the relation between the radius
and
and calculate the
resulting radius of the trajectory. Plot the relation between the radius
and  . Compare your results to the known analytic solution. (assume
non relativistic motion)
. Compare your results to the known analytic solution. (assume
non relativistic motion)
 ,
,  . Construct the Lissajous
curves by setting
. Construct the Lissajous
curves by setting  ,
,  ,
,
 ,
,  . What happens when
. What happens when  ?
?
 vs
vs  and calculate the slope of the resulting straight
line by using the linear least squares method. Is it what you expect?
Calculate the intercept and compare your result with the expected one.
and calculate the slope of the resulting straight
line by using the linear least squares method. Is it what you expect?
Calculate the intercept and compare your result with the expected one.
 for
for  ,
,
 ,
,  using the following steps: First show
that
using the following steps: First show
that  . Then set
. Then set  ,
,  . Vary
. Vary
 and measure the resulting semi-major axis
and measure the resulting semi-major axis  . Determine
the intercept of the resulting straight line in order to calculate
. Determine
the intercept of the resulting straight line in order to calculate  .
.
 ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  . From the
. From the  plot confirm the relation
(
plot confirm the relation
( ,
,
 ,
,  ,
,  ,
,  you obtain that
you obtain that
 for each point
for each point  of the trajectory. The point
of the trajectory. The point  is the center of the force. After determining the semi-major axis
is the center of the force. After determining the semi-major axis  numerically, the point
numerically, the point  will be taken symmetric to
will be taken symmetric to  with respect
to the center of the ellipse.
with respect
to the center of the ellipse.
 and
and  for
different values of
for
different values of  . Calculate the total cross section
. Calculate the total cross section  numerically
and show that it is equal to
numerically
and show that it is equal to  .
.

 . Compute the solutions of the problem numerically in one
dimension and compare them to the known analytic solutions when
. Compute the solutions of the problem numerically in one
dimension and compare them to the known analytic solutions when
 :
:

![[ αx0 ]
C = sin−1 ∘D--−-|E|e----- .
D(D − |E|)](main_latex2476x.png)
 . For
. For  we obtain
we obtain



 is given by a different
relation and not by equation (
is given by a different
relation and not by equation ( and study the transition from open to closed trajectories.
and study the transition from open to closed trajectories.
 (
( ) in the
previous problem. Plot the function
) in the
previous problem. Plot the function  for
for  ,
,
 ,
,  ,
,  , and of course for
, and of course for  . Determine the
equilibrium position and the ionization energy.
. Determine the
equilibrium position and the ionization energy.
 ,
,  ,
,  ,
,  on the plane for
on the plane for  ,
,
 , and
, and  numerically. In the
numerically. In the  case consider the scattering
problem and calculate the functions
case consider the scattering
problem and calculate the functions  ,
,  and the total cross section
and the total cross section
 .
.
 where
where  . Calculate the potential
. Calculate the potential
 and plot the function
and plot the function  . Determine the
equilibrium position and the ionization energy.
. Determine the
equilibrium position and the ionization energy.
 ,
,  and
and  numerically. How much do your results depend on the minimum scattering
angle?
numerically. How much do your results depend on the minimum scattering
angle?
 . Determine appropriate initial conditions that give a spiral
trajectory.
. Determine appropriate initial conditions that give a spiral
trajectory.
 for the Rutherford scattering both
analytically and numerically. What happens to your numerical results as you
vary the integration limits?
for the Rutherford scattering both
analytically and numerically. What happens to your numerical results as you
vary the integration limits?
 static point
charges.
static point
charges.
 plane in a constant magnetic field
plane in a constant magnetic field  . Solve the equations of motion
using a 4th order Runge–Kutta Method. Plot the resulting trajectories for
the initial conditions that you will choose.
. Solve the equations of motion
using a 4th order Runge–Kutta Method. Plot the resulting trajectories for
the initial conditions that you will choose.
 are connected by identical springs. The
springs’ spring constant is equal to
are connected by identical springs. The
springs’ spring constant is equal to  and their equilibrium length is equal
to
and their equilibrium length is equal
to  . The particles move without friction on a horizontal plane. Solve the
equations of motion of the system numerically by using a 4th order
Runge–Kutta Method. Plot the resulting trajectories for the initial
conditions that you will choose. (Hint: Look in the files
. The particles move without friction on a horizontal plane. Solve the
equations of motion of the system numerically by using a 4th order
Runge–Kutta Method. Plot the resulting trajectories for the initial
conditions that you will choose. (Hint: Look in the files 




 and they are connected by an ideal weightless spring with spring
constant
and they are connected by an ideal weightless spring with spring
constant  and equilibrium length
and equilibrium length  . The rods are hinged to the
ceiling at points whose distance is
. The rods are hinged to the
ceiling at points whose distance is  (see figure
(see figure  and
and  . Solve these equations numerically by
using a 4th order Runge–Kutta method. Plot the positions of the
particles in a Cartesian coordinate system and the resulting trajectory.
Study the normal modes for small angles
. Solve these equations numerically by
using a 4th order Runge–Kutta method. Plot the positions of the
particles in a Cartesian coordinate system and the resulting trajectory.
Study the normal modes for small angles  and compute the
deviation of the solutions from the small oscillation approximation as
the angles become larger. (Hint: Look in the files
and compute the
deviation of the solutions from the small oscillation approximation as
the angles become larger. (Hint: Look in the files  axis.
axis.
 .
.
 and one of order
and one of order  ,
and the difference of the results is used as an estimate of the truncation
error. If the error needs to be reduced, the step size is reduced and if it is
satisfactorily small the step size is increased. For the details we refer the
reader to
,
and the difference of the results is used as an estimate of the truncation
error. If the error needs to be reduced, the step size is reduced and if it is
satisfactorily small the step size is increased. For the details we refer the
reader to  . The first three
positions are the coordinates of the initial position and the last three
the components of the initial velocity. Then we set some variables that
determine the behavior of the integration program (see the file
. The first three
positions are the coordinates of the initial position and the last three
the components of the initial velocity. Then we set some variables that
determine the behavior of the integration program (see the file  =
=  =
=  =
=  =
=  =
=
 =
=  we end the
calculation.
we end the
calculation.
 . The program is in the file
. The program is in the file 
 and
and 

 ,
,  .
The components of the acceleration of the particle are:
.
The components of the acceleration of the particle are: 
 ,
,  ,
,  and
and  :
:
































 with
with
 ,
,  and
and  ,
,  .
Note that
.
Note that  . You may also want to calculate the current density from
the equation
. You may also want to calculate the current density from
the equation  .
.
 . The particle’s rest mass is
. The particle’s rest mass is  , its
mass is
, its
mass is  (where
(where  ), its momentum is
), its momentum is  and its
energy is
and its
energy is  . Then the equations of motion in a dynamic field
. Then the equations of motion in a dynamic field
 are given by:
are given by:


 we obtain
we obtain 





 . Given the initial conditions
. Given the initial conditions





 their solution is
unique and it can be computed numerically using the 4th-5th order Runge–Kutta
method according to the discussion of the previous section. By using the relations
their solution is
unique and it can be computed numerically using the 4th-5th order Runge–Kutta
method according to the discussion of the previous section. By using the relations

 ,
,  ,
,  ,
,  ,
,  ,
,  instead. Similarly, from the solutions
instead. Similarly, from the solutions  ,
,  ,
,  ,
,  ,
,
 ,
,  we can calculate
we can calculate  ,
,  ,
,  ,
,  ,
,  ,
,
 . We always have to check that
. We always have to check that


















![( )3 [ ]
B⃗ = B0 RE-- 3 (dˆ⋅ ˆr)ˆr − ˆd ,
r](main_latex2648x.png)
 is the magnetic dipole moment of the Earth’s magnetic field and
is the magnetic dipole moment of the Earth’s magnetic field and
 . The parameter values are approximately equal to
. The parameter values are approximately equal to  ,
,
 , where
, where  is the radius of the Earth. The typical energy of
the moving particles is
is the radius of the Earth. The typical energy of
the moving particles is  MeV which corresponds to velocities of
magnitude
MeV which corresponds to velocities of
magnitude  . We choose
the coordinate axes so that
. We choose
the coordinate axes so that  and we measure distance in
and we measure distance in  units
units






 ,
,  ,
,  . The problem of why the effect is not seen
near the equator is left as an exercise.
. The problem of why the effect is not seen
near the equator is left as an exercise.
 . Assume that their interaction is given by the
Coulomb force only. Write a program that computes their trajectory
numerically using the RK45 method.
. Assume that their interaction is given by the
Coulomb force only. Write a program that computes their trajectory
numerically using the RK45 method.


 . Compute the
three dimensional Lissajous curves which appear for appropriate
values of the angular frequencies
. Compute the
three dimensional Lissajous curves which appear for appropriate
values of the angular frequencies  ,
,  ,
,
 .
.
 are at the fixed positions
are at the fixed positions  and
and
 . A third particle of mass
. A third particle of mass  interacts with them via a
Newtonian gravitational force and moves at non relativistic speeds.
Compute the particle’s trajectory and find initial conditions that result
in a planar motion.
interacts with them via a
Newtonian gravitational force and moves at non relativistic speeds.
Compute the particle’s trajectory and find initial conditions that result
in a planar motion.
 and
and  .
. is given by:
is given by: 
 ,
,  ,
,  and
and
 are the polar coordinates of the point where the electric field is
calculated. Calculate the trajectory of a test charge moving in this
field at non relativistic speeds. Calculate the deviation between the
relativistic and the non relativistic trajectories when the initial speed is
are the polar coordinates of the point where the electric field is
calculated. Calculate the trajectory of a test charge moving in this
field at non relativistic speeds. Calculate the deviation between the
relativistic and the non relativistic trajectories when the initial speed is
 respectively (ignore radiation effects).
respectively (ignore radiation effects).
 .
The electric field is given by
.
The electric field is given by

 axis. The linear charge density is
axis. The linear charge density is  and it is constant. The four straight
lines intersect the
and it is constant. The four straight
lines intersect the  plane at the points
plane at the points  ,
,  ,
,  ,
,
 . Calculate the trajectory of a non relativistic charge in this
field. Next, compute the relativistic trajectories (ignore all radiation
effects).
. Calculate the trajectory of a non relativistic charge in this
field. Next, compute the relativistic trajectories (ignore all radiation
effects).
 interact via their Newtonian gravitational force.
Compute their (non relativistic) trajectories in space.
interact via their Newtonian gravitational force.
Compute their (non relativistic) trajectories in space. point charges
point charges  which are located at fixed positions on the plane
given by their position vectors
which are located at fixed positions on the plane
given by their position vectors  ,
,  . The electric field is given by
Coulomb’s law
. The electric field is given by
Coulomb’s law 
 is the unit vector in the direction of
is the unit vector in the direction of  . The
components of the field are
. The
components of the field are
 is
is

 , i.e. the
curves whose tangent lines at each point are parallel to the electric field at that
point. The magnitude of the electric field is proportional to the density of the field
lines (the number of field lines per perpendicular area). This means that the
electric flux
, i.e. the
curves whose tangent lines at each point are parallel to the electric field at that
point. The magnitude of the electric field is proportional to the density of the field
lines (the number of field lines per perpendicular area). This means that the
electric flux  through a surface
through a surface  is proportional to the number
of field lines that cross the surface. Electric field lines of point charge distributions
start from positive charges (sources), end in negative charges (sinks) or extend to
infinity.
is proportional to the number
of field lines that cross the surface. Electric field lines of point charge distributions
start from positive charges (sources), end in negative charges (sinks) or extend to
infinity.
 , and it
points in the direction of decreasing
, and it
points in the direction of decreasing  . The planar cross sections of the
equipotential surfaces are closed curves which are called equipotential
lines.
. The planar cross sections of the
equipotential surfaces are closed curves which are called equipotential
lines.



 is taken in the direction of the electric field
and we obtain
is taken in the direction of the electric field
and we obtain

 .
.
 is in the
tangential direction of a field line, then
is in the
tangential direction of a field line, then  is in the perpendicular
direction since
is in the perpendicular
direction since  . Therefore the
equations that give the equipotential lines are
. Therefore the
equations that give the equipotential lines are

 we move in the direction
we move in the direction  to the new
position
to the new
position

 and
and  respectively. The next lines call the subroutine
respectively. The next lines call the subroutine  ,
,  ,
,
 ,
,  :
:

 located at the origin
and we draw one field line passing through the point
located at the origin
and we draw one field line passing through the point  .
.
 located at the vertices of a
square:
located at the vertices of a
square:





 ,
,
 ,
,  ,
,  (
(

 of equation (
of equation ( . The size of the drawing area of the curve is set
by the parameter
. The size of the drawing area of the curve is set
by the parameter  , the motion is in the direction of the electric field,
which ends on a negative charge or outside the drawing area (why?). In
order to draw the line in both directions, set
, the motion is in the direction of the electric field,
which ends on a negative charge or outside the drawing area (why?). In
order to draw the line in both directions, set  and repeat the
calculation.
and repeat the
calculation.


 ). The
command
). The
command  to
to  with step equal to
with step equal to
 .
.



 :
:

 in a region of space
in a region of space  bounded by a closed
surface
bounded by a closed
surface  . When the potential is known on
. When the potential is known on  the solution to (
the solution to ( .
.
 . In this case the last term in equation (
. In this case the last term in equation ( is a compact subset of the plane and
is a compact subset of the plane and  is a closed curve.
is a closed curve.
 by a discrete,
square lattice. The potential is defined on the
by a discrete,
square lattice. The potential is defined on the  sites of the lattice. We
take
sites of the lattice. We
take  to be bounded by a square with sides of length
to be bounded by a square with sides of length  . The distance
between the nearest lattice points is called the lattice constant
. The distance
between the nearest lattice points is called the lattice constant  .
. , where
, where  is the number of lattice points on each side of
the square. The continuous solution is approximated by the solution on
the lattice, and the approximation becomes exact in the
is the number of lattice points on each side of
the square. The continuous solution is approximated by the solution on
the lattice, and the approximation becomes exact in the  and
and
 limits, so that the length
limits, so that the length  remains constant. The
curve
remains constant. The
curve  is approximated by the lattice sites that are located on the
perimeter of the square and the loci in the square where the potential takes
constant values. This is a simple model of a set of conducting surfaces
(points where
is approximated by the lattice sites that are located on the
perimeter of the square and the loci in the square where the potential takes
constant values. This is a simple model of a set of conducting surfaces
(points where  const.
const.  ) in a compact region whose boundary is
grounded (points where
) in a compact region whose boundary is
grounded (points where  ). An example is depicted in figure
). An example is depicted in figure 
 according to the equations:
according to the equations:

 and ignoring the
terms implied by
and ignoring the
terms implied by  , we obtain
, we obtain 
 such that
such that
 and
and  where
where  . By taking
. By taking  so that
so that 


 and
and 


 , equation (
, equation (
 is the
arithmetic mean of the potential of the nearest neighbors. We will describe an
algorithm which belongs to the class of “successive overrelaxation methods”
(SOR) whose basic steps are:
is the
arithmetic mean of the potential of the nearest neighbors. We will describe an
algorithm which belongs to the class of “successive overrelaxation methods”
(SOR) whose basic steps are: of the square lattice.
of the square lattice.
 on the vacuum sites. Of
course it is not the solution we are looking for. A good choice will lead
to fast convergence of the algorithm to the true solution. A bad choice
may lead to slow convergence, no convergence or even convergence to
the wrong solution. In our case the problem is easy and the simple
choice
on the vacuum sites. Of
course it is not the solution we are looking for. A good choice will lead
to fast convergence of the algorithm to the true solution. A bad choice
may lead to slow convergence, no convergence or even convergence to
the wrong solution. In our case the problem is easy and the simple
choice  will do.
will do.
 .
. result in
the same solution.
result in
the same solution.
 and the
two conductors are at constant potential
and the
two conductors are at constant potential  and
and  respectively. The
user enters the values
respectively. The
user enters the values  and
and  , the lattice size
, the lattice size  and the required
accuracy interactively. The latter is determined by a small number
and the required
accuracy interactively. The latter is determined by a small number  . The
convergence criterion that we set is that the maximum difference between the
values of the potential between two successive sweeps should be less than
. The
convergence criterion that we set is that the maximum difference between the
values of the potential between two successive sweeps should be less than
 .
.
 with the
with the 
 . In this case the Laplace equation becomes the Poisson
equation:
. In this case the Laplace equation becomes the Poisson
equation:

 .
. 





 .
The reader is asked to reproduce this figure together with figures
.
The reader is asked to reproduce this figure together with figures  and
and  is immediately
updated. In contrast, the Jacobi method uses the
is immediately
updated. In contrast, the Jacobi method uses the  of equation
(
of equation
(
 is a solution of equation (
is a solution of equation ( ,
Jacobi’s method can be formulated as
,
Jacobi’s method can be formulated as

 refer to the values of the potential during
the
refer to the values of the potential during
the  -th sweep. The successive overrelaxation (SOR) method is given
by:
-th sweep. The successive overrelaxation (SOR) method is given
by:
 we have “underrelaxation” and we obtain slower convergence than
the Jacobi method. When
we have “underrelaxation” and we obtain slower convergence than
the Jacobi method. When  we have “overrelaxation” and an
appropriate choice of
we have “overrelaxation” and an
appropriate choice of  can lead to an improvement compared to the Jacobi
method. When
can lead to an improvement compared to the Jacobi
method. When  SOR diverges. Further study of the SOR methods is left as
an exercise to the reader.
SOR diverges. Further study of the SOR methods is left as
an exercise to the reader.
 is proportional
to
is proportional
to  .
.
 at the
point
at the
point  .
.
 from each other.
from each other.
 /
/ and use them in order to choose the values
of the potential on the equipotential lines that you plan to
draw. If e.g. you choose to draw 5 equipotential lines, take
and use them in order to choose the values
of the potential on the equipotential lines that you plan to
draw. If e.g. you choose to draw 5 equipotential lines, take
 and
and 
 .
.
 chosen in the previous step,
draw an equipotential line from that point.
chosen in the previous step,
draw an equipotential line from that point. .
.
 . Vary
. Vary  on
on
 (
( (
(
 of the
system of conductors of the previous problem when
of the
system of conductors of the previous problem when  ,
,  . In
order to calculate the charge
. In
order to calculate the charge  , compute the surface charge density
, compute the surface charge density  using the equation
using the equation

 is the perpendicular component of the electric field on the
surface. Use the approximation
is the perpendicular component of the electric field on the
surface. Use the approximation

 is the potential difference between a point on the conductor and
its nearest neighbor. By integrating (i.e. summing) you can estimate the
total charge on each conductor. If these are opposite and their absolute
value is
is the potential difference between a point on the conductor and
its nearest neighbor. By integrating (i.e. summing) you can estimate the
total charge on each conductor. If these are opposite and their absolute
value is  , then the capacitance can be calculated from the equation
, then the capacitance can be calculated from the equation
 . Perform the calculation described above for
. Perform the calculation described above for  and
and
 . Verify
that the capacitance is independent of
. Verify
that the capacitance is independent of  . Use
. Use  in the corresponding equations in the
program in the file
in the corresponding equations in the
program in the file  and print the results in the file
and print the results in the file  instead of
instead of
 . Take
. Take  in the square
in the square
 ,
,  . Study the convergence of the solutions by plotting
the section
. Study the convergence of the solutions by plotting
the section  for each
for each  ,
,  ,
,  ,
,  ,
, 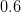 ,
,  ,
,  . What happens when
. What happens when
 ?
?
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . What happens when
. What happens when
 ?
?
 at
time
at
time  if the particle is at
if the particle is at  at
at  . The equation that determines
. The equation that determines
 is
is
 depends on the
details of the system that is studied. For example, for the Brownian
motion of a dust particle in a fluid which moves under the influence of
random collisions with the fluid particles, we have that
depends on the
details of the system that is studied. For example, for the Brownian
motion of a dust particle in a fluid which moves under the influence of
random collisions with the fluid particles, we have that  ,
where
,
where  is the (absolute) temperature of the fluid,
is the (absolute) temperature of the fluid,  is the friction
coefficient
is the friction
coefficient is the Boltzmann constant.
is the Boltzmann constant.
 the particle is localized at one
point
the particle is localized at one
point  , i.e.
, i.e.
 as a probability density implies that for
as a probability density implies that for  we
should have that
we
should have that
 is normalized so that (
is normalized so that ( , the time evolution of
, the time evolution of
 is governed by equation (
is governed by equation ( , then it will hold at all times
if
, then it will hold at all times
if


 and that
and that

 we obtain
we obtain 
 .
.
 for small times is
for small times is


 of space.
of space.  in our
case.
in our
case. is easily
calculated
is easily
calculated
 so that
so that  results
in
results
in  .
.
 and define
and define

 and let
and let  be the temperature distribution
within the rod at time
be the temperature distribution
within the rod at time  . The two ends of the rod are kept at constant
temperature
. The two ends of the rod are kept at constant
temperature  . If the initial temperature distribution in the
rod is
. If the initial temperature distribution in the
rod is  , then the temperature distribution at all times is determined by
the diffusion equation
, then the temperature distribution at all times is determined by
the diffusion equation
 is the thermal
is the thermal is the thermal conductivity,
is the thermal conductivity,  is the density and
is the density and  is the specific heat of the rod.
is the specific heat of the rod.
![x ∈ [0, 1]](main_latex2964x.png) . The function
. The function  , giving the fraction of the temperature
difference to the temperature at the ends of the rod, is dimensionless
and
, giving the fraction of the temperature
difference to the temperature at the ends of the rod, is dimensionless
and







 is in agreement with the
expectation that the rod will have constant temperature at long times, which will
be equal to the temperature at its ends (
is in agreement with the
expectation that the rod will have constant temperature at long times, which will
be equal to the temperature at its ends ( ).
).
![x ∈ [0,1]](main_latex2976x.png) for
for ![t ∈ [0,tf]](main_latex2977x.png) . The problem will be defined on a two dimensional
discrete lattice and the differential equation will be approximated by finite
difference equations.
. The problem will be defined on a two dimensional
discrete lattice and the differential equation will be approximated by finite
difference equations.
 spatial points
spatial points ![xi ∈ [0, 1]](main_latex2979x.png)

 intervals have the same width
intervals have the same width

 time points
time points ![tj ∈ [0,tf]](main_latex2984x.png)

 time intervals have the same duration
time intervals have the same duration


 is approximated by its values on the
is approximated by its values on the  lattice
lattice



 in time
in time

 for all
for all  in the computer
memory.
in the computer
memory.
 of the lattice point
of the lattice point  at a given time slice
at a given time slice  . Therefore it
can be used for all
. Therefore it
can be used for all  . The relations (
. The relations ( and
and  since the values
since the values 
 are kept
constant.
are kept
constant.




 . Therefore we will define only two
arrays
. Therefore we will define only two
arrays  ,
,  and
and  ,
,  which store
the values of
which store
the values of  and
and  at time
at time  respectively. In the program listed below, the names of these arrays are
respectively. In the program listed below, the names of these arrays are 


 ,
,  and
and 
 in
three columns. When a time slice is printed, the program prints an empty line so
that the output is easily read by the three dimensional plotting function
in
three columns. When a time slice is printed, the program prints an empty line so
that the output is easily read by the three dimensional plotting function  can be made with the
can be made with the
 for a fixed value of
for a fixed value of  we first note that an
empty line in the file
we first note that an
empty line in the file  . We save the results in the file
. We save the results in the file






 . We compute the relative error
. We compute the relative error





 for the diffusion, or random walk,
problem, we should impose the normalization condition (
for the diffusion, or random walk,
problem, we should impose the normalization condition ( defined for
defined for ![x ∈ [0, 1]](main_latex3040x.png) the relation
becomes
the relation
becomes
![x ∈ [0,1 ]](main_latex3042x.png) , then the points
, then the points  and
and  are identified and we
obtain
are identified and we
obtain

 , we obtain
, we obtain  ,
,
 .
.
 , we apply equation (
, we apply equation ( ,
,  . In order to take into account the cyclic topology we
take
. In order to take into account the cyclic topology we
take


 is the point
is the point  and the
neighbor to the left of the point
and the
neighbor to the left of the point  is the point
is the point  . For the rest of the points
. For the rest of the points
 equation (
equation ( are chosen so that the particle is located at
are chosen so that the particle is located at
 . For each instant of time we perform measurements in order to verify
the equations (
. For each instant of time we perform measurements in order to verify
the equations ( const.
const.
 and we should check that its value is
conserved and is always equal to 1.
and we should check that its value is
conserved and is always equal to 1.
 is a discrete estimator of
the expectation value of the distance squared from the initial position.
For small enough times it should follow the law given by equation (
is a discrete estimator of
the expectation value of the distance squared from the initial position.
For small enough times it should follow the law given by equation ( ,
,
 and
and  . The latter are measured in order to check if for large enough
times they obtain the
. The latter are measured in order to check if for large enough
times they obtain the  const.
const.

 for all
for all
 ,
,


 ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  ,
,  ,
,  are found in
columns 2, 3, 4, 5, 6 and 7 respectively of the file
are found in
columns 2, 3, 4, 5, 6 and 7 respectively of the file  ,
,  ,
,
 ,
,  ,
,  ,
,  .
. 
















 can be easily confirmed by inspecting the values recorded
in the file
can be easily confirmed by inspecting the values recorded
in the file  can be confirmed with the commands
can be confirmed with the commands
 with the commands
with the commands








 in a thin rod satisfies equation
(
in a thin rod satisfies equation
( . The initial temperature distribution at
. The initial temperature distribution at  is given by
the function
is given by
the function
![{ 0.5 x ∈ [x ,x ]
u(x,0) = 1 2 ,
0.3 x ∕∈ [x1,x2 ]](main_latex3115x.png)
 and
and  .
.
 for
for  ,
,
 ,
,  ,
,  . Take
. Take  and
and  . Do the
same for
. Do the
same for  by choosing appropriate
by choosing appropriate  and keeping
and keeping
 . Plot the functions
. Plot the functions  in the same plot.
in the same plot.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Take
. Take
 and choose an appropriate value for the corresponding
and choose an appropriate value for the corresponding
 .
.
 .
. .
.
 in a thin rod satisfies the
equation
in a thin rod satisfies the
equation

 , and when
, and when

![( [ (2πx)]
{ 0.5 1 − cos -b- 0 ≤ x < b
u(x,0) = 0 b ≤ x ≤ 1 .
(](main_latex3144x.png)
 for
for  ,
,
 and for
and for 
 ,
,  ,
,  , by taking
, by taking
 ,
,  . Do the same for
. Do the same for  by choosing
appropriate
by choosing
appropriate  . Plot the functions
. Plot the functions  in the same plot.
in the same plot.
 ,
,
 and
and  for
for  . Plot the functions
. Plot the functions
 in the same plot.
in the same plot.
 for
for  and
and
 for
for  . Plot the functions
. Plot the functions  in the
same plot. Comment on the effect of the parameter
in the
same plot. Comment on the effect of the parameter  on your
results.
on your
results. in a thin rod of length
in a thin rod of length  satisfies
equation
satisfies
equation

 is the
is the  -dependent thermal diffusivity. The
temperature of the rod at its ends is such that
-dependent thermal diffusivity. The
temperature of the rod at its ends is such that  , and at
time
, and at
time  , the temperature distribution is
, the temperature distribution is

 ,
,  ,
,
 ,
,  ,
,  ,
,  and
and  interactively. On exit, the program
calculates
interactively. On exit, the program
calculates  and writes the points
and writes the points  in two
columns to a file
in two
columns to a file  ,
,  ,
,  ,
,  ,
,  ,
,  and calculate
and calculate  for
for  . Plot the functions
. Plot the functions
 in the same plot.
in the same plot.
 and
and  for
for
 . Plot the functions
. Plot the functions  in the same plot.
in the same plot. as a real
symmetric matrix in an appropriately chosen basis of the Hilbert space
as a real
symmetric matrix in an appropriately chosen basis of the Hilbert space  of
quantum mechanical states. The energy spectrum is obtained from the
eigenvalues of this matrix and the numerical problem reduces to that of
the diagonalization of a real symmetric matrix. Since the Hamiltonian is
represented in
of
quantum mechanical states. The energy spectrum is obtained from the
eigenvalues of this matrix and the numerical problem reduces to that of
the diagonalization of a real symmetric matrix. Since the Hamiltonian is
represented in  by an infinite size matrix, we have to restrict ourselves to a
finite dimensional subspace
by an infinite size matrix, we have to restrict ourselves to a
finite dimensional subspace  of dimension
of dimension  . In this space the
Hamiltonian is represented by an
. In this space the
Hamiltonian is represented by an  real symmetric matrix. The
eigenvalues of this matrix will be calculated numerically using standard
methods and the energy eigenvalues will be obtained in the
real symmetric matrix. The
eigenvalues of this matrix will be calculated numerically using standard
methods and the energy eigenvalues will be obtained in the  limit.
limit.

 ,
,  so that
we can express the above equation using dimensionless terms:
so that
we can express the above equation using dimensionless terms:

 ,
,  and
and  ,
then we obtain
,
then we obtain

 ,
,  and
and  are now dimensionless. The operator
are now dimensionless. The operator  can be
diagonalized with the help of the creation and annihilation operators
can be
diagonalized with the help of the creation and annihilation operators  and
and  ,
defined by the relations:
,
defined by the relations:

![[a, a†] = 1,](main_latex3221x.png)
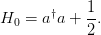
 ,
,  of
of  span the Hilbert space of states
span the Hilbert space of states  and satisfy the relations
and satisfy the relations



 is given by the wavefunctions:
is given by the wavefunctions:
 are the Hermite polynomials.
are the Hermite polynomials.


 in this representation are:
in this representation are: 
 can be calculated from equation (9.12) :
can be calculated from equation (9.12) :

 from the matrix
product of
from the matrix
product of  with itself.
with itself.
 .
.

 of the subspace
of the subspace  of the Hilbert space
of states
of the Hilbert space
of states  . We will restrict ourselves to states within this subspace and we will
use the
. We will restrict ourselves to states within this subspace and we will
use the  dimensional representation matrices of
dimensional representation matrices of  ,
,  and
and  in
in  .
For example, when
.
For example, when  we obtain
we obtain



 of
the
of
the  matrix
matrix  . Instead of reinventing the wheel, we will use ready
made routines that calculate eigenvalues and eigenvectors of matrices found in the
Lapack library. This library can be found in the high quality numerical software
repository
. Instead of reinventing the wheel, we will use ready
made routines that calculate eigenvalues and eigenvectors of matrices found in the
Lapack library. This library can be found in the high quality numerical software
repository  .
The number of rows
.
The number of rows 
 using the same
matrix. The subroutine can be used in two ways:
using the same
matrix. The subroutine can be used in two ways:  . The
eigenvectors are normalized to unity, i.e.
. The
eigenvectors are normalized to unity, i.e. 
 . The
matrix
. The
matrix  of
of  and the coupling constant
and the coupling constant  .
Then the program computes the eigenvalues
.
Then the program computes the eigenvalues  of the
of the  matrix
matrix  , which represents the action of the operator
, which represents the action of the operator  in the
in the
 representation in
representation in  . The tasks are allocated to the
subroutines
. The tasks are allocated to the
subroutines  matrix
matrix  . First, the matrix
. First, the matrix  is
calculated and then
is
calculated and then  is obtained by computing its fourth power. The
matrix
is obtained by computing its fourth power. The
matrix  can also be calculated analytically and this is left as an
exercise to the reader. The subroutine
can also be calculated analytically and this is left as an
exercise to the reader. The subroutine  using the result for
using the result for  given by
given by 


















 and
and  . The
. The  choice leads us
to the simple harmonic oscillator and we obtain the expected solutions:
choice leads us
to the simple harmonic oscillator and we obtain the expected solutions:
 ,
,  and the eigenstates (eigenvectors of
and the eigenstates (eigenvectors of
 )
)  . Similar results can be obtained for larger
. Similar results can be obtained for larger
 .
.
 , the finite
, the finite  calculation contains systematic errors
from neglecting all the matrix elements
calculation contains systematic errors
from neglecting all the matrix elements  for
for  or
or  . Our
program calculates the eigenvalues
. Our
program calculates the eigenvalues  of the finite matrix
of the finite matrix  ,
,
 and one expects that
and one expects that


 -th level eigenvalue of the Hamiltonian
-th level eigenvalue of the Hamiltonian  . In practice the limit
. In practice the limit
 and
and  is calculated by computing
is calculated by computing  numerically for
increasing values of
numerically for
increasing values of  . If convergence to a desired level of accuracy is achieved
for the accessible values of
. If convergence to a desired level of accuracy is achieved
for the accessible values of  , then the approached limit is taken as an
approximation to
, then the approached limit is taken as an
approximation to  . This process is shown graphically in figures
. This process is shown graphically in figures  . Convergence is satisfactory for quite small
. Convergence is satisfactory for quite small  for
for  but
larger values of
but
larger values of  are needed for
are needed for  . Increasing the value of
. Increasing the value of  for fixed
for fixed
 makes the use of larger values of
makes the use of larger values of  necessary. Similarly for a given energy
level
necessary. Similarly for a given energy
level  , increasing
, increasing  also makes the use of larger values of
also makes the use of larger values of  necessary. A
session that computes this limit for the ground level energy
necessary. A
session that computes this limit for the ground level energy  is shown
below
is shown
below convergence of
convergence of  and that we can take
and that we can take  . For higher
accuracy, a computation using larger
. For higher
accuracy, a computation using larger  will be necessary.
will be necessary.
 of an operator
of an operator
 when the anharmonic oscillator is in a state
when the anharmonic oscillator is in a state :
:


 are the eigenvectors of the finite
are the eigenvectors of the finite  matrix
matrix  computed numerically by
computed numerically by  , where
, where



 ,
,  and
and  . Taking into account that
. Taking into account that 
 , we obtain the uncertainties
, we obtain the uncertainties
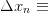

 and
and 
 . Their product
should satisfy
. Their product
should satisfy . The results are
shown in table
. The results are
shown in table 

































 limit. As shown in figure
limit. As shown in figure  dominates in this limit
and the expectation value
dominates in this limit
and the expectation value  decreases. This means that states that
confine the oscillator to a smaller range of
decreases. This means that states that
confine the oscillator to a smaller range of  are favored. This, using the
uncertainty principle, implies that the typical momentum of the oscillator
also increases in magnitude. This is confirmed in figure
are favored. This, using the
uncertainty principle, implies that the typical momentum of the oscillator
also increases in magnitude. This is confirmed in figure  to increase with
to increase with  . In order to
understand quantitatively these competing effects we will use a scaling
argument due to Symanzik. We redefine
. In order to
understand quantitatively these competing effects we will use a scaling
argument due to Symanzik. We redefine  ,
,  in the
Hamiltonian
in the
Hamiltonian  and for large enough
and for large enough  we
obtain
we
obtain
 is the Hamiltonian of the anharmonic “oscillator” with
is the Hamiltonian of the anharmonic “oscillator” with
 . Since the operator
. Since the operator  is independent of
is independent of  , the energy spectrum will
have the asymptotic behavior
, the energy spectrum will
have the asymptotic behavior

 we have that
we have that

 . For large values of
. For large values of  , the authors
obtain the asymptotic behavior
, the authors
obtain the asymptotic behavior


 . This relation is tested
in figure
. This relation is tested
in figure 





















 , therefore
, therefore


 and
and

 and
and  are localized to the left and right well of the
potential respectively (see also figure
are localized to the left and right well of the
potential respectively (see also figure  . The resulting
program can be found in the file
. The resulting
program can be found in the file  and
and  ? The
answer to this question is obtained from the study of the expectation value of the
position operator
? The
answer to this question is obtained from the study of the expectation value of the
position operator  in each one of them. We know that when the particle is in
one of the energy eigenstates, then we have that
in each one of them. We know that when the particle is in
one of the energy eigenstates, then we have that

 is even. Therefore
is even. Therefore 

 and that the amplitudes
and that the amplitudes 
 .
Also
.
Also . Therefore, if we have that
. Therefore, if we have that  and
and
 , we obtain
, we obtain

 , the subroutine
, the subroutine  in the columns of the matrix
in the columns of the matrix 
 with the classical values
with the classical values
 as
as  is increased.
is increased.
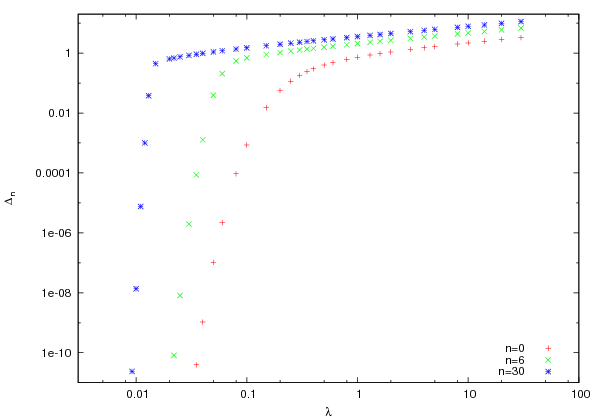




 for
for  analytically. Calculate its
eigenvalues for
analytically. Calculate its
eigenvalues for  . Compare your results with the numerical values
that you obtain from your program.
. Compare your results with the numerical values
that you obtain from your program.
 and that they form an orthonormal basis
and that they form an orthonormal basis  .
.
 and
and  for
for  with an accuracy better
than
with an accuracy better
than  %.
%.
 can you calculate
can you calculate  for
for  with an accuracy
better than
with an accuracy
better than  % when
% when  ?
?
 and
and  for
for  with step
with step  by
achieving accuracy better than
by
achieving accuracy better than  %. How large should
%. How large should  be taken
in each case?
be taken
in each case?
 in the
in the  representation analytically. Modify the program in
representation analytically. Modify the program in
 by computing the exponent (cpu time)
by computing the exponent (cpu time) for
for  .
.
 and
and  . What is the largest value of
. What is the largest value of
 that you can study given your computational resources?
that you can study given your computational resources?
 for
for
 and then fit your results to a function of the form
and then fit your results to a function of the form
 . What is the accuracy in the calculation of
the coefficients
. What is the accuracy in the calculation of
the coefficients  ,
,  and
and  and how good is the agreement with
equation (
and how good is the agreement with
equation ( ,
,  and the corresponding
products
and the corresponding
products  .
.  . Repeat your calculations for
. Repeat your calculations for  .
.
 .
.
 .
.

 for
for  ,
,  and
and  .
.
 ,
,  and the products
and the products  .
Calculate the expectation values
.
Calculate the expectation values  ,
,  and
and  for
for
 ,
,  and
and  .
.
 for
for  and
and  .
Calculate the difference
.
Calculate the difference 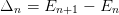 and comment on your
results.
and comment on your
results.

 of the previous problem with
of the previous problem with
 and
and  respectively. Explain your results.
respectively. Explain your results.
 given by equation (
given by equation ( with the
classical values
with the
classical values  for
for  .
.
 for
for  and
and  .
.
 ,
,  . Calculate these
quantities for the anharmonic oscillator and the double well potential for
. Calculate these
quantities for the anharmonic oscillator and the double well potential for
 and
and  . What do you conclude from your
results?
. What do you conclude from your
results?
 , without spin, moving in one
dimension, in a static potential
, without spin, moving in one
dimension, in a static potential  . We will only study bound states. The
solutions in this case yield the discrete energy spectrum
. We will only study bound states. The
solutions in this case yield the discrete energy spectrum  as well as
the corresponding eigenstates of the Hamiltonian
as well as
the corresponding eigenstates of the Hamiltonian  in position
representation.
in position
representation.
 , and one that can be applied to
more general cases. The first method is introduced only for educational
purposes and the reader may skip section
, and one that can be applied to
more general cases. The first method is introduced only for educational
purposes and the reader may skip section  , which are the position representation of the energy
eigenstates, satisfy the Schrödinger equation
, which are the position representation of the energy
eigenstates, satisfy the Schrödinger equation


 . Equation (
. Equation (
 such that
such that  . The numbers
. The numbers  are real and they are the (bound) energy spectrum of the particle in the
potential
are real and they are the (bound) energy spectrum of the particle in the
potential . The minimum energy
. The minimum energy  is called the ground state energy and
is called the ground state energy and . According to
the Heisenberg uncertainty principle, in this state the uncertainties in momentum
. According to
the Heisenberg uncertainty principle, in this state the uncertainties in momentum
 and position
and position  so that
so that 
 form an orthonormal basis
form an orthonormal basis 
 which represents the state
which represents the state
 is given by the linear combination
is given by the linear combination


 are complex numbers
that give the probability
are complex numbers
that give the probability  to measure energy
to measure energy  in the state
in the state
 .
.
 the function
the function

 , i.e. the probability
of detecting the particle in the interval
, i.e. the probability
of detecting the particle in the interval ![[x1,x2]](main_latex3580x.png) is given by
is given by

 axis).
axis).
 of this quantum mechanical system are
functions of the position and the momentum and their quantum mechanical
versions are given by operators
of this quantum mechanical system are
functions of the position and the momentum and their quantum mechanical
versions are given by operators  . Their expectation values when the
system in a state
. Their expectation values when the
system in a state  are given by
are given by
 , the
function
, the
function  and the parameters so that we deal only with dimensionless
quantities. Equation (
and the parameters so that we deal only with dimensionless
quantities. Equation (
 which is defined by the parameters of the
problem
which is defined by the parameters of the
problem . We define
. We define 
 and we obtain
and we obtain


 ,
,  and
change notation to
and
change notation to  ,
,  . We obtain
. We obtain



 and we
obtain
and we
obtain

![[x, p] = iℏ](main_latex3613x.png) becomes
becomes ![[˜x, ˜p] = i](main_latex3614x.png) . The kinetic energy
. The kinetic energy
 is given by
is given by



 instead of
instead of
 .
.

 where a particle is confined within the interval
where a particle is confined within the interval
![[− L∕2,L ∕2]](main_latex3622x.png) :
:

 and the dimensionless variable
and the dimensionless variable  corresponds to
corresponds to  when
when  is measured in length units.
is measured in length units.


 for
for  and one with odd parity
and one with odd parity

 for
for  .
.


 .
.


 depends on the normalization of the wave function. Therefore
we can set
depends on the normalization of the wave function. Therefore
we can set  originally and then renormalize the wave function so
that equation (
originally and then renormalize the wave function so
that equation ( . The problem is that the energy
. The problem is that the energy  is unknown. If the energy
is not allowed by the quantum theory we will find that the boundary
conditions
is unknown. If the energy
is not allowed by the quantum theory we will find that the boundary
conditions

 .
. 







 that is lower than the
one we are looking for. We can use estimates from known solutions
of similar looking potential wells or simply start from a value slightly
higher than the absolute minimum of the potential.
that is lower than the
one we are looking for. We can use estimates from known solutions
of similar looking potential wells or simply start from a value slightly
higher than the absolute minimum of the potential.
 to
to  .
.
 and
we repeat.
and
we repeat.
 changes sign. Then we lower the energy by
changes sign. Then we lower the energy by
 .
.
 for appropriately chosen
small
for appropriately chosen
small  .
. to
to  we use the 4th order
Runge-Kutta method
we use the 4th order
Runge-Kutta method




 and
and  respectively and
respectively and  . The file
. The file 

 changes (
changes ( ). Then the value of the energy is overestimated
and we change the sign of the step
). Then the value of the energy is overestimated
and we change the sign of the step  can be studied. The full program is listed
below:
can be studied. The full program is listed
below:


 . The
convergence can be studied graphically in figure
. The
convergence can be studied graphically in figure  is excellent.
is excellent. 








 are positive numbers. A qualitative plot of these
functions is shown in figure
are positive numbers. A qualitative plot of these
functions is shown in figure  , whereas for the double well
potential
, whereas for the double well
potential  and
and  .
. , the energy levels of all the potentials
that we studied above tend to have identical values. This happens because, when
the particle has energy much larger than
, the energy levels of all the potentials
that we studied above tend to have identical values. This happens because, when
the particle has energy much larger than  , the details of the potential at the
bottom do not influence its dynamical properties very much. For the triangular
potential, the energy levels have higher values than the corresponding ones of the
square potential. This happens because, on the average, the potential energy is
higher and the potential tends to confine the particle to a smaller region (
, the details of the potential at the
bottom do not influence its dynamical properties very much. For the triangular
potential, the energy levels have higher values than the corresponding ones of the
square potential. This happens because, on the average, the potential energy is
higher and the potential tends to confine the particle to a smaller region ( is
decreased, therefore
is
decreased, therefore  is increased). This can be seen in figure
is increased). This can be seen in figure  and
and
 . The first one represents a state where
the particle is localized in the left well and the second one in the right.
This is shown in figure
. The first one represents a state where
the particle is localized in the left well and the second one in the right.
This is shown in figure  the two wells decouple and
the wave functions
the two wells decouple and
the wave functions  become equal to the energy eigenstate wave
functions of two particles in separate infinite square wells of width
become equal to the energy eigenstate wave
functions of two particles in separate infinite square wells of width  with energy eigenvalues
with energy eigenvalues  . The difference of
. The difference of  and
and  from these two values is due to the finite
from these two values is due to the finite  (see problem
(see problem 



















 . We used this
assumption in equations (
. We used this
assumption in equations ( , the wave function is almost zero around
, the wave function is almost zero around  and
the integration from
and
the integration from  to
to  will be dominated by numerical
errors. The same is true when the particle has to go through high potential
barriers.
will be dominated by numerical
errors. The same is true when the particle has to go through high potential
barriers.



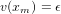






 , the
convergence of the algorithm becomes harder. You can understand this by
realizing that in the integration process the solution is evolved from the classically
allowed into the classically forbidden region so that an oscillating solution
changes into an exponentially damped one. But as
, the
convergence of the algorithm becomes harder. You can understand this by
realizing that in the integration process the solution is evolved from the classically
allowed into the classically forbidden region so that an oscillating solution
changes into an exponentially damped one. But as  there are two
solutions, one that is physically acceptable
there are two
solutions, one that is physically acceptable  and one that is
diverging
and one that is
diverging  which is not acceptable due to (
which is not acceptable due to ( . For this reason it is preferable to integrate from the exponentially
damped region towards the oscillating region. The idea is to start integrating
from these regions and try to match the solutions and their derivatives at
appropriately chosen matching points. The matching is achieved at a
point
. For this reason it is preferable to integrate from the exponentially
damped region towards the oscillating region. The idea is to start integrating
from these regions and try to match the solutions and their derivatives at
appropriately chosen matching points. The matching is achieved at a
point  by trying to determine the value of the energy that sets the
ratio
by trying to determine the value of the energy that sets the
ratio

 within the classical region (
within the classical region ( ) and usually
we pick a turning point
) and usually
we pick a turning point . By renormalizing
. By renormalizing  we can
always set
we can
always set  , therefore
, therefore  means that
means that
 . The denominator of (
. The denominator of ( ,
,  ,
,
 ,
,  . This choice depends on the potential
. This choice depends on the potential
 . Usually we take
. Usually we take 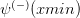 ,
,  to
be zero or exponentially small (e.g.
to
be zero or exponentially small (e.g.  ,
,  ). The
corresponding values of the derivatives
). The
corresponding values of the derivatives  ,
,  are also taken to be small. The arbitrary normalization of
are also taken to be small. The arbitrary normalization of  allows
these initial values to be chosen in a crude way. The relative sign of
the derivatives at large
allows
these initial values to be chosen in a crude way. The relative sign of
the derivatives at large  (determined e.g. by the parity of the wave
function for even potentials) is also taken care by the renormalization
of
(determined e.g. by the parity of the wave
function for even potentials) is also taken care by the renormalization
of  when applying the matching condition. For an infinite well,
the points
when applying the matching condition. For an infinite well,
the points  .
.
 and of the energy variation
step
and of the energy variation
step  .
.
 . Choose the solution that is at the left most side
. Choose the solution that is at the left most side ,
, .
.
 ,
, .
.
 , so that
, so that
 .
.
 of equation (
of equation ( for appropriately chosen
for appropriately chosen  , the calculation ends.
The result for the energy eigenvalue and eigenfunction is considered to
be determined with adequate accuracy and we may proceed with the
analysis of the results.
, the calculation ends.
The result for the energy eigenvalue and eigenfunction is considered to
be determined with adequate accuracy and we may proceed with the
analysis of the results.
 changes sign it means that we have crossed the energy
eigenvalue. Reverse the direction of search by taking
changes sign it means that we have crossed the energy
eigenvalue. Reverse the direction of search by taking  .
.
 and repeat by going back to the fourth
step.
and repeat by going back to the fourth
step. corresponding to the eigenvalue
corresponding to the eigenvalue  . We normalize the
wave function according to equation (
. We normalize the
wave function according to equation ( of the wave function which is related to
of the wave function which is related to  by
by  .
.
 is coded in the function
is coded in the function  ,
,
 ,
,  ,
,  to the calling program. These routines are put in a separate file for each
potential that we want to study. The name of the file is related to the form
of the potential, e.g. we choose
to the calling program. These routines are put in a separate file for each
potential that we want to study. The name of the file is related to the form
of the potential, e.g. we choose 

 ,
,  . The energy of
the ground state is found to be
. The energy of
the ground state is found to be  . The wave
function is stored in the file
. The wave
function is stored in the file 
 on a state
on a state  can be easily calculated in the
position representation by its action on the corresponding wave function
can be easily calculated in the
position representation by its action on the corresponding wave function  .
The action of the operators
.
The action of the operators


 of the
operator
of the
operator  when the system is at the state
when the system is at the state  . Interesting examples are the
observables “position”
. Interesting examples are the
observables “position”  , “position squared”
, “position squared”  , “momentum”
, “momentum”  , “momentum
squared”
, “momentum
squared”  , “kinetic energy”
, “kinetic energy”  , “potential energy”
, “potential energy”  , “energy” or
“Hamiltonian”
, “energy” or
“Hamiltonian”  whose expectation values are given by the relations
whose expectation values are given by the relations
 as well as
equations (10.15) and (10.16) . Especially interesting are the “uncertainties”
as well as
equations (10.15) and (10.16) . Especially interesting are the “uncertainties”
 ,
,  that satisfy the inequality (“Heisenberg’s
uncertainty relation”)
that satisfy the inequality (“Heisenberg’s
uncertainty relation”)

 , we obtain that
, we obtain that
 . Other operators need a numerical approximation
for the calculation of their expectation values. If the values of the wave
function are given at
. Other operators need a numerical approximation
for the calculation of their expectation values. If the values of the wave
function are given at  equally spaced points
equally spaced points  , then we
obtain
, then we
obtain
 and
and

 . Special care should be taken at
the endpoints of the interval
. Special care should be taken at
the endpoints of the interval ![[x ,x ]
1 N](main_latex3831x.png) . As a first approach we will use the naive
approximations
. As a first approach we will use the naive
approximations

 ,
,  ,
,  ,
,  ,
,  ,
,  can be
found in the file
can be
found in the file  in the
format produced by the program in
in the
format produced by the program in  pairs. It is not necessary to have the wave
function properly normalized, the program will take care of it. If this data is
stored in a file
pairs. It is not necessary to have the wave
function properly normalized, the program will take care of it. If this data is
stored in a file  , the value of the
energy
, the value of the
energy ,
,  ,
,  ,
,  ,
,  ,
,  and
and  to the
to the  . In this section we will revisit the problem by using the
position representation. We will calculate the eigenfunctions
. In this section we will revisit the problem by using the
position representation. We will calculate the eigenfunctions  that
diagonalize the Hamiltonian (
that
diagonalize the Hamiltonian ( in equation (
in equation (
 . For
. For  we obtain the harmonic oscillator with
we obtain the harmonic oscillator with

 are the Hermite polynomials.
are the Hermite polynomials.
 ,
,  . You are encouraged to test the
influence of other choices on the results.
. You are encouraged to test the
influence of other choices on the results. 

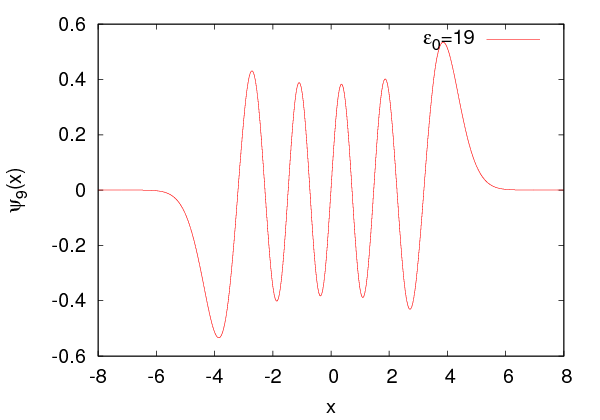



 –
– . The values of the energy
. The values of the energy
 for
for  are in agreement with (
are in agreement with ( .
.
 ,
,  ,
,  ,
,  ,
,  and
and
 . These are easily calculated using equations (
. These are easily calculated using equations ( ,
,  ,
whereas
,
whereas

 with accuracy
with accuracy  and
and
 with accuracy
with accuracy  . The expectation values
. The expectation values  ,
,  are shown
in table
are shown
in table 








 . We copy the file
. We copy the file 



































 the
particle becomes more confined in space as expected. In table
the
particle becomes more confined in space as expected. In table  for
for  . By increasing
. By increasing  ,
,  is increased.
Table
is increased.
Table  ,
,  and
and  for the
anharmonic oscillator for the states
for the
anharmonic oscillator for the states  ,
,  . By increasing
. By increasing  ,
,
 is decreased and
is decreased and  is increased. The product of the
uncertainties
is increased. The product of the
uncertainties  seems to be quite close to the corresponding values for the
harmonic oscillator. The results should be compared with the ones obtained in
table
seems to be quite close to the corresponding values for the
harmonic oscillator. The results should be compared with the ones obtained in
table 
 in (
in ( . Equation (
. Equation (
 are related to the energy values
are related to the energy values  by
by

 . The minimum is
located at
. The minimum is
located at  and its value is
and its value is  . The code for this
potential is in the file
. The code for this
potential is in the file 





























 and
and 
 .
The results are plotted in figure
.
The results are plotted in figure  within the attained accuracy as expected for real, bound
states
within the attained accuracy as expected for real, bound
states can be computed using the Simpson rule
can be computed using the Simpson rule

![[a,b]](main_latex3986x.png) is discretized by
is discretized by  points
points  where
where  is even. Each interval
is even. Each interval ![[x ,x ]
i i+1](main_latex3990x.png) has width
has width  .
.
 of the calculated wave function
of the calculated wave function
 .
.
 . This is the problem of the (finite) potential well.
Solve the problem for
. This is the problem of the (finite) potential well.
Solve the problem for  and
and  . How many bound states do
you find? Next study the influence of the wall on the solutions. Introduce a
parameter
. How many bound states do
you find? Next study the influence of the wall on the solutions. Introduce a
parameter  so that
so that  and study the dependence of the
solutions on
and study the dependence of the
solutions on  . Take
. Take  and
compute the difference of the first two energy eigenvalues. Estimate the
accuracy of the method. Next lower the value of
and
compute the difference of the first two energy eigenvalues. Estimate the
accuracy of the method. Next lower the value of  until there is no
bound state. What is the relation between
until there is no
bound state. What is the relation between  and
and  when this happens?
Compare with the analytic result which you know from your quantum
mechanics course.
when this happens?
Compare with the analytic result which you know from your quantum
mechanics course.  , take
, take  to the double well potential. Observe the (almost)
degenerate states and plot the wave functions
to the double well potential. Observe the (almost)
degenerate states and plot the wave functions  ,
where
,
where  is odd. Compare the results with the corresponding energy levels
and eigenfunctions of the infinite square well. Increase
is odd. Compare the results with the corresponding energy levels
and eigenfunctions of the infinite square well. Increase  to the point
where you cannot solve the problem numerically.
to the point
where you cannot solve the problem numerically.  the numerical effort is increased. For
the numerical effort is increased. For  the wave
function is almost zero and it is hard to obtain the non trivial wave function
for
the wave
function is almost zero and it is hard to obtain the non trivial wave function
for  . As the accuracy deteriorates, you should increase
. As the accuracy deteriorates, you should increase

 and
and

 and
and

 . In each case
calculate
. In each case
calculate  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
![[x1,x2]](main_latex4025x.png) given the wave function calculated
by the program in the file
given the wave function calculated
by the program in the file ![[− x1,x1]](main_latex4026x.png) where the probability to find the particle inside them is equal to
where the probability to find the particle inside them is equal to
 .
.
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  and plot each expectation value as a function of
and plot each expectation value as a function of
 .
.


 for which
for which  . Calculate the
energy levels
. Calculate the
energy levels  of the bound states numerically by setting
of the bound states numerically by setting  in
equation (
in
equation ( . Plot the potential
. Plot the potential  and the
corresponding eigenfunctions. Calculate the expectation values of the
position and momentum, the uncertainties in position and momentum and
their product. Repeat for
and the
corresponding eigenfunctions. Calculate the expectation values of the
position and momentum, the uncertainties in position and momentum and
their product. Repeat for  .
.

 is real. Calculate
is real. Calculate  for the harmonic
oscillator for
for the harmonic
oscillator for  and show (numerically) that
and show (numerically) that  .
.

 ,
,
 ,
,  ,
,  and obtain
and obtain



 ,
,  , and
, and
 is a Laguerre polynomial given by
is a Laguerre polynomial given by 
 . You can take
. You can take
 ,
,  and calculate
and calculate  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 .
.
 and
and  . Calculate the
wavefunctions using the program
. Calculate the
wavefunctions using the program  and compare the two results.
and compare the two results. 


 ,
,  . From
. From  and
and  for
for
 and determine the accuracy achieved by the calculation for
each
and determine the accuracy achieved by the calculation for
each  . For which values of
. For which values of  do you obtain large discrepancies between
your results? Remember that for large
do you obtain large discrepancies between
your results? Remember that for large  , the states of high energy
contribute more than for small
, the states of high energy
contribute more than for small  . Figure
. Figure  does not apply. Second, the geometry of
the path of the random walker has fractal dimension which is larger than
one
does not apply. Second, the geometry of
the path of the random walker has fractal dimension which is larger than
one from which the next one
from which the next one  is generated by
the relation
is generated by
the relation
 ,
,  and
and  . In the bibliography, there is a
lot of discussion on the good and bad choices of
. In the bibliography, there is a
lot of discussion on the good and bad choices of  ,
,  and
and  , which
depend on the programming language and whether we are on a 32–bit
or 64–bit systems. For details see the chapter on random numbers in
, which
depend on the programming language and whether we are on a 32–bit
or 64–bit systems. For details see the chapter on random numbers in
 determines the maximum period
determines the maximum period steps, then
the exact same sequence will be produced and
steps, then
the exact same sequence will be produced and  will be the period of the
sequence. Since there are at most
will be the period of the
sequence. Since there are at most  different numbers, the period is at most
equal to
different numbers, the period is at most
equal to  . For a bad choice of
. For a bad choice of  ,
,  and
and  the period will be much smaller.
But
the period will be much smaller.
But  cannot be arbitrarily large since there is a maximum number of bits that
computers use for the storage of integers. For 4-byte (32 bit) unsigned integers the
maximum number is
cannot be arbitrarily large since there is a maximum number of bits that
computers use for the storage of integers. For 4-byte (32 bit) unsigned integers the
maximum number is  , whereas for signed integers
, whereas for signed integers  . One can
prove
. One can
prove ,
,  and
and  results in a sequence which is a permutation
results in a sequence which is a permutation
 of the numbers
of the numbers  . This is good enough for simple
applications that require fast random number generation but for serious
calculations one has to carefully balance efficiency with quality. Good quality
random generators are more complicated algorithms and their states are
determined by more than one integer. If you need the source code for such
generators you may look in the bibliography, like in e.g.
. This is good enough for simple
applications that require fast random number generation but for serious
calculations one has to carefully balance efficiency with quality. Good quality
random generators are more complicated algorithms and their states are
determined by more than one integer. If you need the source code for such
generators you may look in the bibliography, like in e.g.  ,
,  and
and  :
: ,
,  and
and  . This is the choice of
Lewis, Goodman and Miller (1969) and provides a generator that passes
many tests and, more importantly, it has been used countless of times
successfully. One technical problem is that, when we multiply
. This is the choice of
Lewis, Goodman and Miller (1969) and provides a generator that passes
many tests and, more importantly, it has been used countless of times
successfully. One technical problem is that, when we multiply  by
by  ,
we may obtain a number which is outside the range of 4-byte integers
and this will result in an “integer overflow”. In order
,
we may obtain a number which is outside the range of 4-byte integers
and this will result in an “integer overflow”. In order positive, 32-bit (4 byte), signed integers. Schrage has proposed to use the
relation
positive, 32-bit (4 byte), signed integers. Schrage has proposed to use the
relation![( [ ]
|| a (xi− 1 modq ) − r xi−1- if it is ≥ 0
{ [ q ]
(axi−1) modm = | a (xi− 1 modq ) − r xi−q1- + m if it is < 0
|(](main_latex4123x.png)
 ,
, ![q = [m ∕a ]](main_latex4125x.png) and
and  . One can show that if
. One can show that if
 and if
and if  , then
, then  ,
,
![0 ≤ r[xi−1∕q] ≤ m − 1](main_latex4130x.png) and that (
and that ( . The proof of the above statements is left as an exercise to the
reader.
. The proof of the above statements is left as an exercise to the
reader. which appears once in the sequence. This
adds a
which appears once in the sequence. This
adds a  % overhead, depending on the compiler. If you don’t
care about that, you may remove the line. Note that the number
% overhead, depending on the compiler. If you don’t
care about that, you may remove the line. Note that the number  , where
, where , which are subsequently mapped on
the plane. This is done by taking the integer part of the numbers
, which are subsequently mapped on
the plane. This is done by taking the integer part of the numbers  with
with  and
and  is the random number produced by the
generator:
is the random number produced by the
generator:
 points used in the plots in figures
points used in the plots in figures  that it produces, do not pass the
that it produces, do not pass the  test when we have more
than
test when we have more
than  points, which is much less than the period of the generator. In order to
avoid such problems, there are many solutions that have been proposed and the
simplest among them “shuffle” the results so that the low order serial
correlations vanish. Such generators will be discussed in the next section.
points, which is much less than the period of the generator. In order to
avoid such problems, there are many solutions that have been proposed and the
simplest among them “shuffle” the results so that the low order serial
correlations vanish. Such generators will be discussed in the next section.


 . The reciprocal of the number following the option
. The reciprocal of the number following the option








 of the sample, we calculate the standard
deviation
of the sample, we calculate the standard
deviation
 is the sequence of random numbers. Figure
is the sequence of random numbers. Figure 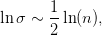

 we can use a sequence of uniformly distributed random
numbers in the interval
we can use a sequence of uniformly distributed random
numbers in the interval  as follows: Consider the cumulative distribution
function
as follows: Consider the cumulative distribution
function
 in the interval
in the interval ![(− ∞, x]](main_latex4157x.png) and it
is equal to the probability
and it
is equal to the probability  . If
. If  is uniformly distributed in the
interval
is uniformly distributed in the
interval  then we have that
then we have that  . Therefore
. Therefore  is such
that
is such
that  and follows the
and follows the  distribution. Therefore, if
distribution. Therefore, if
 form a sequence of uniformly distributed random numbers, then the
numbers
form a sequence of uniformly distributed random numbers, then the
numbers

 .
.






 is the error function. The error function, as
well as its inverse, can be calculated numerically, but this would result in a slow
computation. A trick to make a more efficient calculation is to consider the
probability density
is the error function. The error function, as
well as its inverse, can be calculated numerically, but this would result in a slow
computation. A trick to make a more efficient calculation is to consider the
probability density  of
of  and
and 

 ,
,  . Then we have that
. Then we have that


 of uniformly distributed
random numbers and take
of uniformly distributed
random numbers and take 
 , which follow the
Gaussian distribution
, which follow the
Gaussian distribution is listed below:
is listed below:



 (this is what the
“flag”
(this is what the
“flag”  . The state of the generator is
determined by more than one numbers. In order to use it we should learn
. The state of the generator is
determined by more than one numbers. In order to use it we should learn
 ,
, . The minimum distance between
the lattice sites is
. The minimum distance between
the lattice sites is  (lattice constant). The vector that describes the change of
the position of the particle during the
(lattice constant). The vector that describes the change of
the position of the particle during the  -th jump is a random variable
-th jump is a random variable  and it
always has the same magnitude
and it
always has the same magnitude  . This means that, given the
position
. This means that, given the
position  of the particle at time
of the particle at time  , its position
, its position  at time
at time
 is
is


 and
and  are uncorrelated for
are uncorrelated for  and we have that
and we have that

 are equally probable, therefore we obtain
are equally probable, therefore we obtain

 occur with the same frequency and they cancel each other.
Therefore
occur with the same frequency and they cancel each other.
Therefore  for
for  . Since the magnitude of the vectors
. Since the magnitude of the vectors  is
constant, we obtain
is
constant, we obtain

 of length
of length  to occur
is
to occur
is
 is the number of nearest neighbors of a lattice site. This
probability depends on the length of the path and not on its geometry.
This can be easily seen using the obvious relation
is the number of nearest neighbors of a lattice site. This
probability depends on the length of the path and not on its geometry.
This can be easily seen using the obvious relation  ,
since there are exactly
,
since there are exactly  equally probable cases. The partition function
is
equally probable cases. The partition function
is

 .
.
 the particle is displaced from its original position
by
the particle is displaced from its original position
by




 .
.


 means asymptotic behavior in the limit
means asymptotic behavior in the limit  . For a classical
walker
. For a classical
walker  , whereas for the random walker
, whereas for the random walker  .
.
 with equal probability.
The SAW is a NRRW with the additional requirement that, when the
walker ends in a previously visited position, the ... walking ends! Some
models studied in the literature include, besides the infinite repulsive force,
an attractive contribution to the total energy for every pair of points of
the path that are nearest neighbors. In this case, each path is weighted
with the corresponding Boltzmann weight according to equation (
with equal probability.
The SAW is a NRRW with the additional requirement that, when the
walker ends in a previously visited position, the ... walking ends! Some
models studied in the literature include, besides the infinite repulsive force,
an attractive contribution to the total energy for every pair of points of
the path that are nearest neighbors. In this case, each path is weighted
with the corresponding Boltzmann weight according to equation ( .
Even though the paths differ microscopically, their long distance properties are
the same. They are examples of models belonging to the same
.
Even though the paths differ microscopically, their long distance properties are
the same. They are examples of models belonging to the same 
 such that for
such that for  we have similar behavior
given by equation (
we have similar behavior
given by equation ( the attractive interaction
dominates, the paths collapse and we obtain
the attractive interaction
dominates, the paths collapse and we obtain  . For
. For  we
have that
we
have that  . For more information we refer the reader to the book of Binder
and Heermann
. For more information we refer the reader to the book of Binder
and Heermann  ,
,  , etc
, etc
 is written to
is written to
 of the points visited by the walker
in each path is written to
of the points visited by the walker
in each path is written to  is chosen and it
is added in the current position
is chosen and it
is added in the current position  . The choice on
. The choice on  is made in
the line
is made in
the line
 because the function
because the function  . We use the construct
. We use the construct 

 for
for  which confirm equation
(
which confirm equation
( .
. 




 in the first column and with
in the first column and with  in the second. The
command
in the second. The
command going through the points (
going through the points ( ,
, ). You can also use the
). You can also use the  , where
, where  is the number of measurements. For the same
reason
is the number of measurements. For the same
reason
 . Construct the plot
of relative frequencies together with the plot of the probability density
function.
. Construct the plot
of relative frequencies together with the plot of the probability density
function.
 . Construct the plot of relative
frequencies together with the plot of the probability density function.
. Construct the plot of relative
frequencies together with the plot of the probability density function.
 random numbers using the function
random numbers using the function  then
then
 and we obtain a linear relation between displacement–length of
path. The quantity
and we obtain a linear relation between displacement–length of
path. The quantity  is the expectation value of the speed of the particle.
Compute
is the expectation value of the speed of the particle.
Compute  for large values of
for large values of  .
.
 and the rest equal
to
and the rest equal
to  . Compute the expectation values
. Compute the expectation values  and
and  and use them
to calculate the average speed of the particle. Check the validity of the
relations
and use them
to calculate the average speed of the particle. Check the validity of the
relations  and
and 
 . What is the
relation between
. What is the
relation between  ,
,  and
and  ?
?
 , she should run the command
, she should run the command  . Calculate
. Calculate  and
and  numerically for
numerically for  . Are they really equal to zero? Why? How
does this depend on the number of measurements?
. Are they really equal to zero? Why? How
does this depend on the number of measurements?
 . What happens as
. What happens as  ?
Why?
?
Why?
 .
.
 can
you simulate? Check whether the CPU time for computing a given number
of random walks increases exponentially with
can
you simulate? Check whether the CPU time for computing a given number
of random walks increases exponentially with  . Search the internet
for the most efficient algorithm that simulates the SAW for large
. Search the internet
for the most efficient algorithm that simulates the SAW for large
 .
. . For simple macroscopic systems
. For simple macroscopic systems  –
–  . For such
systems, it is practically impossible to solve the microscopic equations that
govern their dynamics. Even if we could, the solution would have had much
more information than we need (and capable of analyzing!). It is enough,
however, to know a small number of bulk properties of the system in
order to have a useful description of it. E.g. it is enough to know the
internal energy and magnetization of a magnet or the energy and density of
a fluid instead of the detailed knowledge of the position, momentum,
energy and angular momentum of each particle they are made of. These
quantities provide a thermodynamic description of a system. Statistical
physics makes an attempt to derive these quantities from the microscopic
degrees of freedom and their dynamics given by the Hamiltonian of the
system.
. For such
systems, it is practically impossible to solve the microscopic equations that
govern their dynamics. Even if we could, the solution would have had much
more information than we need (and capable of analyzing!). It is enough,
however, to know a small number of bulk properties of the system in
order to have a useful description of it. E.g. it is enough to know the
internal energy and magnetization of a magnet or the energy and density of
a fluid instead of the detailed knowledge of the position, momentum,
energy and angular momentum of each particle they are made of. These
quantities provide a thermodynamic description of a system. Statistical
physics makes an attempt to derive these quantities from the microscopic
degrees of freedom and their dynamics given by the Hamiltonian of the
system.
 . The energy spectrum of those states is assumed to consist of discrete
values
. The energy spectrum of those states is assumed to consist of discrete
values . This system is in contact and interacts with a large
heat reservoir
. This system is in contact and interacts with a large
heat reservoir .
. which give the probability to find
the system in a state
which give the probability to find
the system in a state  at time
at time  . These weights are the connection between the
microscopic and statistical description of the system. When this system is in
thermal equilibrium with the reservoir, its statistical properties are described by
the, so called,
. These weights are the connection between the
microscopic and statistical description of the system. When this system is in
thermal equilibrium with the reservoir, its statistical properties are described by
the, so called,  be the transition rates
be the transition rates  , i.e.
, i.e.

 is
is 
 is equal to
the rate that the system comes into the state
is equal to
the rate that the system comes into the state  from
from  , minus the rate of leaving the state
, minus the rate of leaving the state  . The second equation is a
result of the probability interpretation of the weights
. The second equation is a
result of the probability interpretation of the weights  and states
that the probability of finding the system in any state is equal to 1 at all
times.
and states
that the probability of finding the system in any state is equal to 1 at all
times.
 are assumed to be time independent
and then the above system of equations for
are assumed to be time independent
and then the above system of equations for  is linear with real
parameters. This, together with the constraint
is linear with real
parameters. This, together with the constraint  , implies
that
, implies
that and the system reaches equilibrium. Then, the
and the system reaches equilibrium. Then, the
 converge to finite numbers
converge to finite numbers  . These are the equilibrium occupation
probabilities
. These are the equilibrium occupation
probabilities 
 ,
with
,
with  , the probabilities
, the probabilities  follow the Boltzmann distribution (Gibbs
1902)
follow the Boltzmann distribution (Gibbs
1902)

 will be frequently
referred to as simply “the temperature” of the system, although, strictly speaking,
it is the inverse of it. Its appearance in the exponential in equation (
will be frequently
referred to as simply “the temperature” of the system, although, strictly speaking,
it is the inverse of it. Its appearance in the exponential in equation ( is simply a conversion constant between units of
energy
is simply a conversion constant between units of
energy in equation (
in equation ( implies
implies

 , one is interested only in the average value of such a quantity. This
is because the probability of measuring the quantity to take a value significantly
different from its average is ridiculously small. The average, or
, one is interested only in the average value of such a quantity. This
is because the probability of measuring the quantity to take a value significantly
different from its average is ridiculously small. The average, or 
 whose value in a state
whose value in a state  is
is  is equal
to
is equal
to

 for a typical thermodynamic
system is such that
for a typical thermodynamic
system is such that

 from its expectation value
from its expectation value
 can be neglected. The limit
can be neglected. The limit  is the so called
is the so called  of the
system
of the
system

 of a thermodynamic system is defined by
of a thermodynamic system is defined by
 is the
is the 

 the free energy becomes the ground state
energy
the free energy becomes the ground state
energy only the lowest energy term in equation (12.11) survives.
For this reason, equation (12.10) gives
only the lowest energy term in equation (12.11) survives.
For this reason, equation (12.10) gives  , which is the third law of
thermodynamics.
, which is the third law of
thermodynamics.
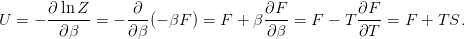
 to the microscopic degrees of freedom can be
derived from equations (
to the microscopic degrees of freedom can be
derived from equations (





 Equation (
Equation ( . In such a case,
. In such a case,  counts,
more or less, the number of states of the system with energy close to
counts,
more or less, the number of states of the system with energy close to
 .
.
 is
is .
Then the probability
.
Then the probability  to measure energy
to measure energy  in the canonical ensemble
is
in the canonical ensemble
is

 , we obtain
, we obtain


 is the number of degrees of freedom of the system and
is the number of degrees of freedom of the system and  is a constant.
is a constant.






 and the deviation
and the deviation  is a measure of the energy
fluctuations. The ratio
is a measure of the energy
fluctuations. The ratio  drops with
drops with  as
as  . Indeed, the
function
. Indeed, the
function


 decreases),
decreases),  shifts to larger values.
shifts to larger values.  is
proportional to the system size. By Taylor expanding around
is
proportional to the system size. By Taylor expanding around  we obtain
we obtain

 . Therefore
. Therefore



 has more than one equally probable
maxima
has more than one equally probable
maxima








 is given by a distribution function
is given by a distribution function
 which can be derived from the Boltzmann distribution (
which can be derived from the Boltzmann distribution ( and
all its higher order moments, i.e. the expectation values
and
all its higher order moments, i.e. the expectation values 
 . The most commonly studied moment is the second moment
(
. The most commonly studied moment is the second moment
( )
)

 is a measure of the fluctuations
of
is a measure of the fluctuations
of  away from its expectation value
away from its expectation value  . When
. When  we obtain
we obtain





 , this role is played by
, this role is played by  ). For a magnetic system in a
constant magnetic field
). For a magnetic system in a
constant magnetic field  , such a quantity is the magnetization
, such a quantity is the magnetization . If
. If  is
the magnetization of the system in the sate
is
the magnetization of the system in the sate  and we assume that its direction is
parallel to the direction of the magnetic field
and we assume that its direction is
parallel to the direction of the magnetic field  , then the Hamiltonian of the
system is
, then the Hamiltonian of the
system is


 in the
Hamiltonian. The quantities
in the
Hamiltonian. The quantities  and
and  are called conjugate
are called conjugate /
/ ) in a gas
or the chemical potential/number of particles (
) in a gas
or the chemical potential/number of particles ( /
/ ) in the grand canonical
ensemble.
) in the grand canonical
ensemble.





 is defined by the equation
is defined by the equation

 . Then the magnetic field
. Then the magnetic field  is a function of the position
is a function of the position  and
interacts with the spin
and
interacts with the spin  so that
so that


 is
is


 and
and  are strongly correlated, i.e. they “vary together”
in the random samples that we take, the function (
are strongly correlated, i.e. they “vary together”
in the random samples that we take, the function ( and
and  are not at all correlated with
each other, the terms
are not at all correlated with
each other, the terms  in the sum over
in the sum over  in the
expectation value
in the
expectation value  cancel each other and
cancel each other and  is
zero
is
zero



 takes its maximum value
takes its maximum value  for
for  .
Then it falls off quite fast. For a generic system
.
Then it falls off quite fast. For a generic system

 is the distance between the points
is the distance between the points  and
and  . The
. The  , is a characteristic length scale of the system which is a measure of the
distance where there is a measurable correlation between the magnetic moments
of two lattice sites. It depends on the parameters that define the system
, is a characteristic length scale of the system which is a measure of the
distance where there is a measurable correlation between the magnetic moments
of two lattice sites. It depends on the parameters that define the system
 . It is important to stress that it is a length scale that arises
. It is important to stress that it is a length scale that arises
 or the lattice
constant
or the lattice
constant  are parameters of the system which don’t depend on the dynamics. In
most of the cases,
are parameters of the system which don’t depend on the dynamics. In
most of the cases,  is of the order of a few lattice constants
is of the order of a few lattice constants  and such a
system does not exhibit correlations at macroscopic scales (i.e. of the order of
and such a
system does not exhibit correlations at macroscopic scales (i.e. of the order of
 ).
).
 . This can happen by fine tuning the parameters
on which
. This can happen by fine tuning the parameters
on which  depends on to their
depends on to their  falls
off like a power (see figure
falls
off like a power (see figure 
 is the number of dimensions of space and
is the number of dimensions of space and  a
a  . Then the system is not sensitive to the
short distance details of the lattice and its dynamics are very well approximated
by continuum space dynamics. Then we say that we obtain the
. Then the system is not sensitive to the
short distance details of the lattice and its dynamics are very well approximated
by continuum space dynamics. Then we say that we obtain the  ,
,

 of a statistical system in the canonical
ensemble approximately. For this reason we construct a sample
of a statistical system in the canonical
ensemble approximately. For this reason we construct a sample states
states 


 which are distributed according to a chosen
probability distribution
which are distributed according to a chosen
probability distribution  . We define the
. We define the  of
of  to
be
to
be

 , and we expect that
, and we expect that

 so that the convergence of (
so that the convergence of ( , and equation (
, and equation (
 in a generic model. According to equation (
in a generic model. According to equation (
 is the probability of measuring energy
is the probability of measuring energy  in the system. A
qualitative plot of
in the system. A
qualitative plot of  is shown in figure
is shown in figure  and
and  , therefore for
, therefore for  and
and  the
qualitative behavior of the respective
the
qualitative behavior of the respective  distributions is shown in figure
distributions is shown in figure 




 in equation (
in equation ( const. in this
case
const. in this
case we
have to obtain a good sample in the region where the product
we
have to obtain a good sample in the region where the product  is
relatively important. The probability of obtaining a state such that
is
relatively important. The probability of obtaining a state such that  is
non negligible is very small when we use the
is
non negligible is very small when we use the  distribution. This can be
seen pictorially in figure
distribution. This can be
seen pictorially in figure  .
.
 . If we choose a sample with probability
. If we choose a sample with probability


 and
the calculation of the expectation values (
and
the calculation of the expectation values ( . This extra effort, however, is much smaller than the one required in order to
overcome the overlap problem discussed in the previous subsection.
. This extra effort, however, is much smaller than the one required in order to
overcome the overlap problem discussed in the previous subsection.
 is not possible in a
direct way. For example, if we attempt to construct a sample according to
is not possible in a
direct way. For example, if we attempt to construct a sample according to
 by picking a state
by picking a state  by chance and add it to the sample with
probability
by chance and add it to the sample with
probability  , then we have a very small probability to accept that state in the
sample. Therefore, the difficulty of constructing the sample runs into the same
overlap problem as in the case of simple sampling. For this reason we construct a
, then we have a very small probability to accept that state in the
sample. Therefore, the difficulty of constructing the sample runs into the same
overlap problem as in the case of simple sampling. For this reason we construct a
 , puts the system in a new state
, puts the system in a new state  in such a way that it
has the
in such a way that it
has the 
 from the
state
from the
state  to a new state
to a new state  satisfy the following requirements:
satisfy the following requirements:
 and
and  and not on the path that the
system has followed on order to get to the sate
and not on the path that the
system has followed on order to get to the sate  (memorylessness)
(memorylessness)

 , i.e. the system has a
nonzero probability to remain in the same state
, i.e. the system has a
nonzero probability to remain in the same state
 the sample
the sample  follows the
follows the  distribution.
distribution. . We may imagine that
this construction happens in “time”
. We may imagine that
this construction happens in “time”  . In a Monte Carlo
. In a Monte Carlo so that the convergence 4. is
fast.
so that the convergence 4. is
fast.
 can become a non trivial task. If it turns out
not to be a typical state of the sample, then it could take a long “time” for the
system to “equilibrate”, i.e. for the Markov process to start sampling
states typical of the simulated temperature. The required time for this to
happen is called the
can become a non trivial task. If it turns out
not to be a typical state of the sample, then it could take a long “time” for the
system to “equilibrate”, i.e. for the Markov process to start sampling
states typical of the simulated temperature. The required time for this to
happen is called the  and/or
and/or
 .
.
 it is possible to
reach any other state
it is possible to
reach any other state  in a finite number of steps. If this criterion is
not satisfied and a significant part of phase space is not sampled, then
sampling will fail. Usually, given a state
in a finite number of steps. If this criterion is
not satisfied and a significant part of phase space is not sampled, then
sampling will fail. Usually, given a state  , the reachable states
, the reachable states  at
the next step (i.e. the states for which
at
the next step (i.e. the states for which  ) are very few.
Therefore the ergodicity of the algorithm considered must be checked
carefully
) are very few.
Therefore the ergodicity of the algorithm considered must be checked
carefully distribution, the transition probabilities should be such that
distribution, the transition probabilities should be such that

 is equal to the
rate in which it leaves
is equal to the
rate in which it leaves  . From equation (
. From equation (

 after sufficiently long thermalization time.
By summing both sides of (
after sufficiently long thermalization time.
By summing both sides of (
 that satisfy condition (
that satisfy condition (
 and calculate the estimators
and calculate the estimators  from equation (
from equation ( has been
achieved.
has been
achieved.


 and
and

 for any other state
for any other state  . In order for (
. In order for ( has to be chosen so that
has to be chosen so that

 in two independent parts
in two independent parts

 is the
is the  when the
system is in the state
when the
system is in the state  . Therefore the first step in the algorithm is to select a
state
. Therefore the first step in the algorithm is to select a
state  with probability
with probability  .
.
 . If the
answer is no, then the system remains in the state
. If the
answer is no, then the system remains in the state  . This way equation
(
. This way equation
( are called the
are called the and that the states
and that the states  are as much as
possible statistically independent from the original state
are as much as
possible statistically independent from the original state  . An ideal situation is
to have
. An ideal situation is
to have  for all
for all  for which
for which  . As we will see in a
following chapter, this is what happens in the case of the Wolff cluster
algorithm.
. As we will see in a
following chapter, this is what happens in the case of the Wolff cluster
algorithm.
 Ising Model
Ising Model




 . The geometry is determined by the distance of the
nearest neighbors, the
. The geometry is determined by the distance of the
nearest neighbors, the  , and the number of sites
, and the number of sites  .
Each side consists of
.
Each side consists of  sites so that
sites so that  , where
, where  is
the dimension of space. The topology is determined by the way sites are
connected with each other via links. Special care is given to the sites
located on the sides of the lattice. We usually take
is
the dimension of space. The topology is determined by the way sites are
connected with each other via links. Special care is given to the sites
located on the sides of the lattice. We usually take 






 or
or  . For the ferromagnetic model, each link
is a “bond” whose energy is higher when the spins on each side of the
link are pointing in the same direction and lower when they point in the
opposite
. For the ferromagnetic model, each link
is a “bond” whose energy is higher when the spins on each side of the
link are pointing in the same direction and lower when they point in the
opposite whose direction is parallel to the direction of the
spins.
whose direction is parallel to the direction of the
spins.
 lattice sites (or
lattice sites (or  . The lattice has
. The lattice has  links (or
links (or 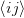 , where
, where  is the pair of vertices on each side of the
link. We identify the sides of the square like in figure
is the pair of vertices on each side of the
link. We identify the sides of the square like in figure 
 . The Hamiltonian of the system is given
by
. The Hamiltonian of the system is given
by
 the system is
ferromagnetic.
the system is
ferromagnetic. case. A link connecting
same spins has energy
case. A link connecting
same spins has energy  , whereas a link connecting opposite spins
has energy
, whereas a link connecting opposite spins
has energy  . The difference of the energy between the two states
is
. The difference of the energy between the two states
is  and the spin-spin dynamics favor links connecting same spins.
The minimum energy
and the spin-spin dynamics favor links connecting same spins.
The minimum energy  is
is . This is equal to
. This is equal to

![∑ ∑ ∑ −βH [{si}] ∑ βJ∑ ⟨ij⟩sisj+βB ∑i si
Z = ... e ≡ e ,
s1= ±1s2=±1 sN= ±1 {si}](main_latex4678x.png)
 is a spin configuration of the system
is a spin configuration of the system , which is equal to
, which is equal to  , i.e.
it increases exponentially with
, i.e.
it increases exponentially with  . For a humble
. For a humble  lattice we have
lattice we have
 terms.
terms.
 has the interesting property that,
for
has the interesting property that,
for  , where
, where
 ) and a
) and a  ). The magnetization
). The magnetization  distinguishes between the two phases and it is called the
distinguishes between the two phases and it is called the  is the Curie temperature
is the Curie temperature , but it is non
analytic
, but it is non
analytic



 the correlation function (
the correlation function ( . The correlation
length
. The correlation
length

 , the magnetization
, the magnetization
 and the magnetic susceptibility
and the magnetic susceptibility  according to the relations
according to the relations
 and nonzero magnetic field
and nonzero magnetic field  behaves
like
behaves
like


 model. The partition function (
model. The partition function ( limit, where the finite
limit, where the finite  analytic functions converge to a non analytic one. The loss of analyticity is
related to the appearance of long distance correlations between the spins
and the scaling of the correlation length according to equation (
analytic functions converge to a non analytic one. The loss of analyticity is
related to the appearance of long distance correlations between the spins
and the scaling of the correlation length according to equation ( symmetry
represented by the transformation
symmetry
represented by the transformation  . The magnetization is zero in the
disordered, high temperature phase and non zero in the ordered, low temperature
phase. This implies that the magnetization is a non analytic function of the
temperature
. The magnetization is zero in the
disordered, high temperature phase and non zero in the ordered, low temperature
phase. This implies that the magnetization is a non analytic function of the
temperature limit. In our case, this
occurs by tuning only one parameter, the temperature, to its critical value. A
unique, dynamical, length scale emerges from the correlation function, the
correlation length
limit. In our case, this
occurs by tuning only one parameter, the temperature, to its critical value. A
unique, dynamical, length scale emerges from the correlation function, the
correlation length  . Scale invariance
. Scale invariance when
when  . In the
critical region, all quantities which are functions of the distance become functions
only of the ratio
. In the
critical region, all quantities which are functions of the distance become functions
only of the ratio  . Everything depends on the long wavelength fluctuations
required by the symmetry of the order parameter and all models in the same
universality class have the same long distance behavior. This way one
can study only the simplest model within a universality class in order to
deduce the large distance/long wavelength properties of all systems in the
class.
. Everything depends on the long wavelength fluctuations
required by the symmetry of the order parameter and all models in the same
universality class have the same long distance behavior. This way one
can study only the simplest model within a universality class in order to
deduce the large distance/long wavelength properties of all systems in the
class.
 sites on each side so that
sites on each side so that  is
the number of lattice sites (vertices) and
is
the number of lattice sites (vertices) and  is the number of links (bonds)
between the sites. The relation
is the number of links (bonds)
between the sites. The relation  holds because we choose helical
boundary conditions as shown in figure
holds because we choose helical
boundary conditions as shown in figure  we have one degree of
freedom, the “spin”
we have one degree of
freedom, the “spin”  which takes on two values
which takes on two values  . We consider the
case of zero magnetic field
. We consider the
case of zero magnetic field  , therefore the Hamiltonian is given
by
, therefore the Hamiltonian is given
by
 is a sum over the
is a sum over the  , corresponding to the pairs of sites
, corresponding to the pairs of sites
 . Then
. Then  since each bond is counted twice in the
second sum. The partition function is
since each bond is counted twice in the
second sum. The partition function is ![∑ ∑ ∑ ∑ ∑
Z = ... e−βH[{si}] ≡ eβ ⟨ij⟩sisj.
s1=±1 s2= ±1 sN=±1 {si}](main_latex4733x.png)
 . According to (
. According to ( is
is

 is the
is the  when the system is in
the state
when the system is in
the state  and
and  is the
is the 
 . In order that the system changes states often enough, the
probabilities
. In order that the system changes states often enough, the
probabilities  should be of order one and the differences in the
energy
should be of order one and the differences in the
energy  should not be too large. This means that the product of
the temperature with the energy difference should be a number of order
one or less. One way to accomplish this is to consider states that differ
by the value of the spin on only one site
should not be too large. This means that the product of
the temperature with the energy difference should be a number of order
one or less. One way to accomplish this is to consider states that differ
by the value of the spin on only one site  . Since the
energy (
. Since the
energy ( nearest neighbors, the change of the spin on
site
nearest neighbors, the change of the spin on
site  results in a change of sign for
results in a change of sign for  terms
terms  in (
in ( . If the state
. If the state  is given by
is given by
 and the state
and the state  by
by  (i.e. all the spins
are the same except the spin
(i.e. all the spins
are the same except the spin  which changes sign), the energy difference will
be
which changes sign), the energy difference will
be

 is randomly chosen then
is randomly chosen then



 .
Remember that we should have
.
Remember that we should have  and
and  . Therefore
. Therefore





 on the change in energy for
different values of
on the change in energy for
different values of  . We observe that this probability is small even
for zero energy change and we expect this method not to perform very
well.
. We observe that this probability is small even
for zero energy change and we expect this method not to perform very
well.

 which are defined on
which are defined on  lattice
sites. The most important part in designing the data structure in a lattice
simulation is to define the neighboring relations among the lattice sites
in the computer memory and this includes the implementation of the
boundary conditions. A bad choice of boundary conditions will make
the effect of the boundary on the results to be large and increase the
lattice
sites. The most important part in designing the data structure in a lattice
simulation is to define the neighboring relations among the lattice sites
in the computer memory and this includes the implementation of the
boundary conditions. A bad choice of boundary conditions will make
the effect of the boundary on the results to be large and increase the




 ,
,  . Each spin is stored in an array
. Each spin is stored in an array 

 to
to  . This is shown in figures
. This is shown in figures  , as shown in figures
, as shown in figures 



 when necessary. Therefore in a program that we want to
calculate the four nearest neighbors
when necessary. Therefore in a program that we want to
calculate the four nearest neighbors  - all spins aligned) or a “hot” (
- all spins aligned) or a “hot” ( - all
spins are equal to
- all
spins are equal to  with equal probability
with equal probability  ) initial configuration.
For large lattices, it is desirable to start in one of these states and then
lower/increase the temperature in small steps. Each time that the temperature is
changed, the spin configuration is saved and used in the next simulation.
) initial configuration.
For large lattices, it is desirable to start in one of these states and then
lower/increase the temperature in small steps. Each time that the temperature is
changed, the spin configuration is saved and used in the next simulation.  and consider the
transition to a new state
and consider the
transition to a new state  which differs only by the
value of the spin
which differs only by the
value of the spin  (spin flip), whereas all the other spins are the
same:
(spin flip), whereas all the other spins are the
same: 
 . The energy difference between the two states is
. The energy difference between the two states is

 , which you can prove
easily by examining the cases
, which you can prove
easily by examining the cases  separately. The important property of
this relation is that it is local since it depends only on the nearest neighbors. The
calculation of the energy difference
separately. The important property of
this relation is that it is local since it depends only on the nearest neighbors. The
calculation of the energy difference  is fast and is always a number of order
one
is fast and is always a number of order
one . If the energy decreases, i.e.
. If the energy decreases, i.e.  , the new state
, the new state  is
accepted and “we flip the spin”. If the energy increases, i.e.
is
accepted and “we flip the spin”. If the energy increases, i.e.  , then
the acceptance ratio is
, then
the acceptance ratio is  . In order to accept the new
state with this probability we pick a random number uniformly distributed in
. In order to accept the new
state with this probability we pick a random number uniformly distributed in
 . The probability that this number is
. The probability that this number is  is equal
to
is equal
to . Therefore if
. Therefore if  the change is accepted. If
the change is accepted. If
 the change is rejected and the system remains in the same state
the change is rejected and the system remains in the same state
 .
.
 and these are the only values that enter in the
calculation of
and these are the only values that enter in the
calculation of  . Moreover, only the values that increase the energy, i.e.
. Moreover, only the values that increase the energy, i.e.
 are of interest to us. Therefore we only need two values of
are of interest to us. Therefore we only need two values of  , which
depend only on the temperature. These can by calculated once and for all in
the initialization phase of the program, stored in an array and avoid the
repeated calculation of the exponential
, which
depend only on the temperature. These can by calculated once and for all in
the initialization phase of the program, stored in an array and avoid the
repeated calculation of the exponential  which is expensive.
which is expensive.


 has a
has a  symmetry because it is symmetric under reflection
of all the spins. The probability of appearance of a state depends only
on the value of
symmetry because it is symmetric under reflection
of all the spins. The probability of appearance of a state depends only
on the value of  , therefore two configurations with opposite spin are
equally probable. But such configurations have opposite magnetization,
therefore the average magnetization
, therefore two configurations with opposite spin are
equally probable. But such configurations have opposite magnetization,
therefore the average magnetization  will be zero due to this
cancellation
will be zero due to this
cancellation and its nearest neighbors. The energy
difference is already calculated by (
and its nearest neighbors. The energy
difference is already calculated by (
 , then the calculation of the magnetization
using the first method requires
, then the calculation of the magnetization
using the first method requires  additions per
additions per  Monte Carlo steps,
whereas the second one requires
Monte Carlo steps,
whereas the second one requires  additions per measurement.
additions per measurement. 
 , where
, where  for
the ground state in which all
for
the ground state in which all  links have energy equal to
links have energy equal to  . The
magnetization per site is
. The
magnetization per site is

 , where
, where  for
for  (perfect disorder) and
(perfect disorder) and
 for the ground state at
for the ground state at  (perfect order). We call
(perfect order). We call  the
order parameter since its value determines the phase that the system is
in.
the
order parameter since its value determines the phase that the system is
in.


 independent
measurements the statistical error drops as
independent
measurements the statistical error drops as  . The problem of
determining how often we have independent measurements is very important and
it will be discussed in detail later in this chapter.
. The problem of
determining how often we have independent measurements is very important and
it will be discussed in detail later in this chapter.
 is a constant parameter, whereas the arrays and variables
encoding the spins and the simulation parameters are put in common
blocks. The array
is a constant parameter, whereas the arrays and variables
encoding the spins and the simulation parameters are put in common
blocks. The array  . The variable
. The variable  and the array
and the array
 according to the discussion on page
according to the discussion on page  -
-  and
and  excluded. The parameters
excluded. The parameters  direction and
direction and  direction.
direction.


 . Those probabilities are going to be
used when
. Those probabilities are going to be
used when  and the possible values are obtained when this
expression takes the values 2 and 4. These are the values stored in the array
and the possible values are obtained when this
expression takes the values 2 and 4. These are the values stored in the array
 , when it is positive.
, when it is positive.
 with equal probability. The probability that
with equal probability. The probability that  in which case we set
in which case we set  ) we set
) we set
 in (
in ( . If it
turns out to be negative, then the change in energy is negative and the spin flip is
accepted. If it turns out to be positive, then we apply the criterion set by (
. If it
turns out to be negative, then the change in energy is negative and the spin flip is
accepted. If it turns out to be positive, then we apply the criterion set by ( and that the data is enough to fill the array
and that the data is enough to fill the array

















 and
and  initial measurements until the
expectation value of the magnetization stabilizes within the limits of its statistical
error.
initial measurements until the
expectation value of the magnetization stabilizes within the limits of its statistical
error.
 , correlations between configurations obtained after a few
sweeps remain strong. It is easy to understand why this is happening.
As the correlation length
, correlations between configurations obtained after a few
sweeps remain strong. It is easy to understand why this is happening.
As the correlation length  (
( (e.g. energy,
magnetization, etc) and let
(e.g. energy,
magnetization, etc) and let  be its value after Monte Carlo “time”
be its value after Monte Carlo “time”  .
.  can be measured in sweeps or multiples of it. The autocorrelation function
can be measured in sweeps or multiples of it. The autocorrelation function  of
of  is
is

 is the average value over the configurations in the sample for
is the average value over the configurations in the sample for
 . The normalization is such that
. The normalization is such that  .
.
 after time
after time  is strongly
correlated to the one at
is strongly
correlated to the one at  , then the product in the numerator in
(
, then the product in the numerator in
( will be
positive. When the correlation is weak, the product will be positive and
negative the same number of times and
will be
positive. When the correlation is weak, the product will be positive and
negative the same number of times and  will be almost zero. In the
case of anti-correlations
will be almost zero. In the
case of anti-correlations  is negative. Negative values of
is negative. Negative values of  occur, but these are artifacts of the finite size of the sample and should be
rejected.
occur, but these are artifacts of the finite size of the sample and should be
rejected.
 drops exponentially
drops exponentially

 is the time scale of decorrelation of the measurements of
is the time scale of decorrelation of the measurements of  and it is called the
and it is called the
 . After time
. After time  ,
,  has dropped to the
has dropped to the  of its initial value and then we say that we have an independent measurement
of
of its initial value and then we say that we have an independent measurement
of . Therefore, if we have
. Therefore, if we have  measurements, the number of independent
measurements of
measurements, the number of independent
measurements of  is
is 
 sweeps. If the cost
of measurement is not significant, then we usually measure more often, since there
is still statistical information even in slightly correlated configurations. An
accurate determination of
sweeps. If the cost
of measurement is not significant, then we usually measure more often, since there
is still statistical information even in slightly correlated configurations. An
accurate determination of  is not easy since it requires measuring for
is not easy since it requires measuring for  .
.












 ). We calculate the function
). We calculate the function  and we see that a fit to equation
(
and we see that a fit to equation
( sweeps. The calculation is performed on a
sample of
sweeps. The calculation is performed on a
sample of  measurements with 1 measurement/sweep. Therefore the number
of independent measurements is
measurements with 1 measurement/sweep. Therefore the number
of independent measurements is  .
.
 . Its definition stems from equation (
. Its definition stems from equation (
 and
and  differ slightly due to systematic errors that come from the
corrections
differ slightly due to systematic errors that come from the
corrections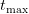

 we observe a plateau in the plot of the value of
we observe a plateau in the plot of the value of
 which indicates convergence, and we take this as the estimator of
which indicates convergence, and we take this as the estimator of
 . For even larger
. For even larger  , finite sample effects enter in the sum that should be
discarded.
, finite sample effects enter in the sum that should be
discarded.








 sweeps, which
is somewhat smaller than the autocorrelation time that we calculated
using the exponential fit to the autocorrelation function. If we are
interested in the scaling properties of the autocorrelation time with the
size of the system
sweeps, which
is somewhat smaller than the autocorrelation time that we calculated
using the exponential fit to the autocorrelation function. If we are
interested in the scaling properties of the autocorrelation time with the
size of the system  or the temperature
or the temperature  , then this difference is not
important
, then this difference is not
important is quicker since it involves no
fitting
is quicker since it involves no
fitting







 . As we approach the critical region,
autocorrelation times increase. At the critical region we observe scaling of their
values with the system size, which means that for large
. As we approach the critical region,
autocorrelation times increase. At the critical region we observe scaling of their
values with the system size, which means that for large  we have that
we have that















 measurements
measurements
 , their mean is an estimator of
, their mean is an estimator of 



 , then according to equation
, then according to equation
 independent measurements. One can
show that in this case, the statistical error in the measurement of
independent measurements. One can
show that in this case, the statistical error in the measurement of  is
is
 , then we obtain equation (
, then we obtain equation (

 independent measurements (we
assumed that
independent measurements (we
assumed that  ). The above relation is consistent with our
assumption that measurements become independent after time
). The above relation is consistent with our
assumption that measurements become independent after time  .
.
 and
and  (or
(or  on each
configuration
on each
configuration  ). After these are calculated on the sample, the error
). After these are calculated on the sample, the error  is not a simple function of
is not a simple function of  and
and  . This is because of the
correlation between the two quantities and the well known formula of
error propagation
. This is because of the
correlation between the two quantities and the well known formula of
error propagation  cannot be
applied.
cannot be
applied.
 measurements, she can put them in
measurements, she can put them in  “bins” and
each bin is to be taken as an independent measurement. This will be
true if the number of measurements per bin
“bins” and
each bin is to be taken as an independent measurement. This will be
true if the number of measurements per bin  . If
. If 
 is average value of
is average value of  in the bin
in the bin  , then the error is given by
(
, then the error is given by
(
 (see
equation (
(see
equation ( . If
. If  is not a priori known we compute the error (
is not a priori known we compute the error ( . When the error is not increasing anymore and takes on
a constant value, then the calculation converges to the true statistical
error.
. When the error is not increasing anymore and takes on
a constant value, then the calculation converges to the true statistical
error.
 bins which contain
bins which contain  elements as
follows: The bin
elements as
follows: The bin  contains the part of the sample obtained after we
we
contains the part of the sample obtained after we
we  -th bin of the binning method from the
full sample
-th bin of the binning method from the
full sample  . The procedure is depicted in figure
. The procedure is depicted in figure 





 in each bin and we obtain
in each bin and we obtain
 . Then the statistical error in the measurement of
. Then the statistical error in the measurement of  is
is


 random samples as follows: We choose one of the
random samples as follows: We choose one of the  measurements
with equal probability. We repeat
measurements
with equal probability. We repeat  times using the
times using the  measurements - i.e. by putting the chosen measurements back to the sample. This
means that on the average
measurements - i.e. by putting the chosen measurements back to the sample. This
means that on the average  of the sample will consist of the
same measurements. In each sample
of the sample will consist of the
same measurements. In each sample  we calculate the average
values
we calculate the average
values  and from those
and from those


 is
is

 without an a priori knowledge of
without an a priori knowledge of  . For more details, the
reader is referred to the articles of Bradley Efron
. For more details, the
reader is referred to the articles of Bradley Efron  measurements
measurements  ,
then we can use the following estimator for the autocorrelation function, given by
equation (
,
then we can use the following estimator for the autocorrelation function, given by
equation (

 is chosen so that
is chosen so that  .
.
 , the second one is
, the second one is  and the third one is
and the third one is  (equation (
(equation ( we do the following:
we do the following:
 . The
. The  stabilizes and
the
stabilizes and
the is minimized
is minimized of the fit can be read off from the output of the command
of the fit can be read off from the output of the command
 . We stress that this is the
. We stress that this is the  doubles its minimum value, we find that
doubles its minimum value, we find that  .
.
 .
.










 . We find that the data for
the autocorrelation function fit perfectly to the function
. We find that the data for
the autocorrelation function fit perfectly to the function

 fit is excellent and the
result for the dominant autocorrelation time is
fit is excellent and the
result for the dominant autocorrelation time is  . The
secondary autocorrelation times are
. The
secondary autocorrelation times are  ,
,  which are
considerably smaller that
which are
considerably smaller that  .
.
 and then
we use equation (
and then
we use equation ( ,
,  ,
,  and
and
 .
. lattice sites
(
lattice sites
( (-b 0.4407). It starts the simulation from a hot
configuration (
(-b 0.4407). It starts the simulation from a hot
configuration ( and
and  with their errors using the program
with their errors using the program  and their error by the factor
and their error by the factor  in order to obtain
in order to obtain
 .
.
 ,
,  and
measure the magnetization per site (
and
measure the magnetization per site ( measurements
using the commands:
measurements
using the commands:
 . The integrated autocorrelation time is found to be
. The integrated autocorrelation time is found to be
 .
.
 . The application of equation
(
. The application of equation
( . Using equation (
. Using equation ( .
The error of the magnetic susceptibility cannot be calculated this way.
.
The error of the magnetic susceptibility cannot be calculated this way.






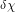



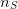 so that the optimal number of samples is
be determined. Figure
so that the optimal number of samples is
be determined. Figure 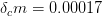 for quite small
number of samples. The analysis could have safely used
for quite small
number of samples. The analysis could have safely used  . In the
case of the magnetic susceptibility, convergence is slower, but we can
still use
. In the
case of the magnetic susceptibility, convergence is slower, but we can
still use 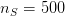 . We obtain
. We obtain  and
and  . The error
assumes independent measurements, something that is not true in our case.
We should use the correction factor
. The error
assumes independent measurements, something that is not true in our case.
We should use the correction factor  which gives
which gives  .
Therefore
.
Therefore

 . The a priori knowledge
of
. The a priori knowledge
of  is necessary in this calculation.
is necessary in this calculation. 

































 . The errors are calculated for a variable number of bins
. The errors are calculated for a variable number of bins
 . Figure
. Figure  the
samples consist of all the measurements except one. Then the error is equal to the
error calculated using the standard deviation formula and it is underestimated by
the factor
the
samples consist of all the measurements except one. Then the error is equal to the
error calculated using the standard deviation formula and it is underestimated by
the factor  . This is shown in figure
. This is shown in figure  . The effect of the autocorrelations
vanishes when we delete
. The effect of the autocorrelations
vanishes when we delete  measurements from each bin. This
happens when
measurements from each bin. This
happens when  . Of
course this an order of magnitude estimate and a careful study is necessary in
order to determine the correct value for
. Of
course this an order of magnitude estimate and a careful study is necessary in
order to determine the correct value for  . Figure
. Figure  to the value
to the value  , which is quite close to
the value
, which is quite close to
the value  . We note that, by using a small number
. We note that, by using a small number
 , we obtain an acceptable estimate, a rule of the thumb that can be
used for quick calculations.
, we obtain an acceptable estimate, a rule of the thumb that can be
used for quick calculations.
 , where the
error converges to the value
, where the
error converges to the value  , in accordance with the previous
estimates. For
, in accordance with the previous
estimates. For  the error converges to the underestimated error
the error converges to the underestimated error
 .
.
 ,
,  without calculating
without calculating  directly. The
data is split into
directly. The
data is split into 
 . Each
jackknife bin contains
. Each
jackknife bin contains  data elements and we apply the bootstrap
method on this data, by taking
data elements and we apply the bootstrap
method on this data, by taking  samples of
samples of  random data. Then
each jackknife bin gives a measurement on which we apply equation (
random data. Then
each jackknife bin gives a measurement on which we apply equation ( and the true
error
and the true
error  using one of the methods described above, we can calculate
using one of the methods described above, we can calculate  using
the relation
using
the relation  . Therefore
. Therefore

 using all the methods described here, these relations can also
be used in order to check the analysis for self-consistency and see if they agree.
This is not always a trivial work since a system may have many autocorrelation
times which influence each observable in a different way (fast modes, slow
modes).
using all the methods described here, these relations can also
be used in order to check the analysis for self-consistency and see if they agree.
This is not always a trivial work since a system may have many autocorrelation
times which influence each observable in a different way (fast modes, slow
modes).

 on the temperature and
the size of the system. Take
on the temperature and
the size of the system. Take  and
and 






 . Then take
. Then take  ,
, 



 . Repeat for the same values of
. Repeat for the same values of  for
for  and
and
 .
.
 . Repeat for
. Repeat for  .
Compare your results with
.
Compare your results with  and
and  .
.
 and
and  as a function
of
as a function
of  (see figure
(see figure  and
and  as a
function of
as a
function of  (see figure
(see figure  (see equation (
(see equation ( for
for  and
and  at an interesting
range of temperatures. Use different initial configuration in order to
study the thermalization of the system as
at an interesting
range of temperatures. Use different initial configuration in order to
study the thermalization of the system as  increases: Cold state with
spins parallel to
increases: Cold state with
spins parallel to  , cold state with spins antiparallel to
, cold state with spins antiparallel to  and hot
state. Study the dependence of the critical temperature separating the
ordered from the disordered state on the value of
and hot
state. Study the dependence of the critical temperature separating the
ordered from the disordered state on the value of  .
.
 has a
first order phase transition, i.e. a discontinuity in the value of the order
parameter which in our case is the magnetization as a function of
has a
first order phase transition, i.e. a discontinuity in the value of the order
parameter which in our case is the magnetization as a function of  . Near
a first order transition we observe the phenomenon of hysteresis. In order to
see it, set
. Near
a first order transition we observe the phenomenon of hysteresis. In order to
see it, set  and
and  and
and

 using as an initial state the last
one coming from the previous step. Do 100 sweeps and calculate
using as an initial state the last
one coming from the previous step. Do 100 sweeps and calculate
 .
.
 .
Stop when
.
Stop when  .
.
 until
until  .
.
 until
until  .
. . What do you observe?
. What do you observe?
 sweeps per point. Plot the time series of
the magnetization and observe the transitions from the metastable
state to the stable one and backwards. Compute the histogram of
the values of the magnetization and determine which state is the
metastable in each case. How is the histogram changing as
sweeps per point. Plot the time series of
the magnetization and observe the transitions from the metastable
state to the stable one and backwards. Compute the histogram of
the values of the magnetization and determine which state is the
metastable in each case. How is the histogram changing as  is
increased?
is
increased?
 instead of
instead of  . Look into
chapter 13.1.2 of Newman and Barkema (esp. figure 13.4). Compute the
change in energy for each spin flip for the Metropolis step. Calculate the
maxima of the magnetic susceptibility and of the specific heat and see if
they are close to the expected critical temperature
. Look into
chapter 13.1.2 of Newman and Barkema (esp. figure 13.4). Compute the
change in energy for each spin flip for the Metropolis step. Calculate the
maxima of the magnetic susceptibility and of the specific heat and see if
they are close to the expected critical temperature  .
Note that even though
.
Note that even though  is different than the corresponding value
on the square lattice, the critical exponents are the same due to
universality.
is different than the corresponding value
on the square lattice, the critical exponents are the same due to
universality.
 to be the
to be the
 coordinate. Set
coordinate. Set
 and compute the energy, the
and compute the energy, the  , the specific heat, the
magnetic susceptibility
, the specific heat, the
magnetic susceptibility  and the
and the  .
.
 has a maximum in the region
has a maximum in the region  . Compute its value at this
temperature for
. Compute its value at this
temperature for  . Show that
. Show that  does not diverge as
does not diverge as  ,
therefore
,
therefore  does not show a phase transition.
does not show a phase transition.
 . What do you conclude? Compare the
behavior of
. What do you conclude? Compare the
behavior of  for the antiferromagnetic Ising model with
for the antiferromagnetic Ising model with  of the
ferromagnetic.
of the
ferromagnetic.










 , or equivalently as the reduced
temperature
, or equivalently as the reduced
temperature
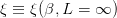 , calculated in
, calculated in 
 , which are the same for all
systems in the same
, which are the same for all
systems in the same  , when
, when  . Systems with the same long distance behavior, but which
could possibly differ microscopically, belong to the same
. Systems with the same long distance behavior, but which
could possibly differ microscopically, belong to the same  these details become irrelevant and all these systems
have the same long distance behavior. Microscopic degrees of freedom of
systems in the same universality class can be quite different, as is the
case of the liquid/vapor phase transition at the triple point and the Ising
model.
these details become irrelevant and all these systems
have the same long distance behavior. Microscopic degrees of freedom of
systems in the same universality class can be quite different, as is the
case of the liquid/vapor phase transition at the triple point and the Ising
model.



 . For a finite
lattice, all observables are analytic since they are calculated from the
analytic
. For a finite
lattice, all observables are analytic since they are calculated from the
analytic given by equation (
given by equation ( the
model behaves approximately as the infinite system. As
the
model behaves approximately as the infinite system. As  and
and 
 and
and  , on the finite
lattice have a maximum for a
, on the finite
lattice have a maximum for a  for which we have
that
for which we have
that

 , we have
that
, we have
that 

 , therefore equations
(
, therefore equations
(


 , but
they can also be evaluated at any temperature in the
, but
they can also be evaluated at any temperature in the  , but one can also use e.g.
, but one can also use e.g.

 according
to (
according
to (
 in this region, and we
obtain equation (
in this region, and we
obtain equation ( . When
. When  we have the effect of critical
slowing down.
we have the effect of critical
slowing down.
 is
concerned
is
concerned .
But the measurement of a local quantity, like
.
But the measurement of a local quantity, like  , for a given number
of times requires no extra cost, since each configuration yields
, for a given number
of times requires no extra cost, since each configuration yields  measurements
measurements is preferable, since it reduces
finite size effects. We see that, in the absence of critical slowing down, the cost of
measurement of
is preferable, since it reduces
finite size effects. We see that, in the absence of critical slowing down, the cost of
measurement of  is
is  .
.
 , making the large
, making the large  simulations
prohibitively expensive. For the Metropolis algorithm on the two dimensional
Ising model we have that
simulations
prohibitively expensive. For the Metropolis algorithm on the two dimensional
Ising model we have that  ; and the problem is severe. Therefore, it is
important to invent new algorithms that beat critical slowing down. In the case of
the Ising model and similar spin systems, the solution is relatively easy. It is
special to the specific dynamics of spin systems and does not have a universal
application.
; and the problem is severe. Therefore, it is
important to invent new algorithms that beat critical slowing down. In the case of
the Ising model and similar spin systems, the solution is relatively easy. It is
special to the specific dynamics of spin systems and does not have a universal
application.
 . As we approach the critical temperature
. As we approach the critical temperature  from the
disordered phase, the typical configurations are dominated by large clusters of
same spins. The Metropolis algorithm makes at most one spin flip per step and
the acceptance ratios for spins inside a cluster are small. For example, a spin with
four same neighboring spins can flip with probability
from the
disordered phase, the typical configurations are dominated by large clusters of
same spins. The Metropolis algorithm makes at most one spin flip per step and
the acceptance ratios for spins inside a cluster are small. For example, a spin with
four same neighboring spins can flip with probability 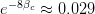 ,
which is quite small. The spins that change more often are the ones with
more neighbors having opposite spins, therefore the largest activity is
observed at the boundaries of the large clusters. In order to obtain a
statistically independent configuration, we need to destroy and create
many clusters, something that happens very slowly using the Metropolis
algorithm who realizes this process mostly by moving the boundaries of the
clusters.
,
which is quite small. The spins that change more often are the ones with
more neighbors having opposite spins, therefore the largest activity is
observed at the boundaries of the large clusters. In order to obtain a
statistically independent configuration, we need to destroy and create
many clusters, something that happens very slowly using the Metropolis
algorithm who realizes this process mostly by moving the boundaries of the
clusters.

 , whereas large clusters
of size
, whereas large clusters
of size  should dominate for
should dominate for  .
.
 . If
. If  is
properly chosen, the detailed balance condition (
is
properly chosen, the detailed balance condition ( , the cluster is enclosed by the dashed line. The new state
, the cluster is enclosed by the dashed line. The new state  is obtained
by flipping all the spins in the cluster, leaving the rest of the spins to be the
same.
is obtained
by flipping all the spins in the cluster, leaving the rest of the spins to be the
same.
 will yield equation (
will yield equation (
 and
and
 . This can be seen in the simple example of figure
. This can be seen in the simple example of figure  of the new state
of the new state  and the acceptance ratio
and the acceptance ratio
 , so that
, so that

 !
!
 is the probability of constructing a
particular cluster and can be split in three factors:
is the probability of constructing a
particular cluster and can be split in three factors:


 is the
probability to include all cluster members found in the
is the
probability to include all cluster members found in the  , the corresponding term is exactly the same since
the two clusters are exactly the same (the only differ by the value of the
spin)!
, the corresponding term is exactly the same since
the two clusters are exactly the same (the only differ by the value of the
spin)!

 is the probability to include a nearest neighbor of same spin to
the cluster, the probability of saying “no” is
is the probability to include a nearest neighbor of same spin to
the cluster, the probability of saying “no” is  . Assume that we have
. Assume that we have  “bonds”
“bonds” , and that we have
, and that we have  such bonds in the state
such bonds in the state  . In figure
. In figure  and
and  . Therefore, the probability to stop the cluster in
the state
. Therefore, the probability to stop the cluster in
the state  is to say “no”
is to say “no”  times, which happens with probability
times, which happens with probability
 :
:

 stops at the same boundary with
probability
stops at the same boundary with
probability


 decreases the energy by 2 and each bond destroyed increases the energy
by 2:
decreases the energy by 2 and each bond destroyed increases the energy
by 2:

![m− nA (μ → ν ) −2β(m −n) A(μ → ν) [ 2β ]n−m
(1 − Padd) ----------= e ⇒ ----------= e (1 − Padd) .
A (ν → μ ) A(ν → μ)](main_latex5372x.png)


 given by (
given by ( .
This is the first new member of the cluster
.
This is the first new member of the cluster
 .
The original spin is not a “new member” anymore
.
The original spin is not a “new member” anymore







 depends on the temperature
depends on the temperature  . It is quite small for
. It is quite small for
 and almost 1 for
and almost 1 for  . Therefore, in the first case the algorithm
favors very small clusters (they are of size 1 for
. Therefore, in the first case the algorithm
favors very small clusters (they are of size 1 for  ) and in the second
case it favors large clusters. In the high temperature regime, we have
almost random spin flips, like in the Metropolis algorithm. In the low
temperature regime, we have large probability of flipping the dominant cluster of
the lattice. This is clearly seen in figure
) and in the second
case it favors large clusters. In the high temperature regime, we have
almost random spin flips, like in the Metropolis algorithm. In the low
temperature regime, we have large probability of flipping the dominant cluster of
the lattice. This is clearly seen in figure  is plotted as a function of the
temperature. For small
is plotted as a function of the
temperature. For small  ,
,  whereas for large
whereas for large  ,
,  .
.





 , most of the time the algorithm chooses a lattice site
randomly and constructs a small cluster around it and flips its spins. The
Metropolis algorithm picks a lattice site randomly and flips it most of the
times. In both cases, the two algorithms function almost the same way and
construct the high temperature disordered spin configurations. For large
, most of the time the algorithm chooses a lattice site
randomly and constructs a small cluster around it and flips its spins. The
Metropolis algorithm picks a lattice site randomly and flips it most of the
times. In both cases, the two algorithms function almost the same way and
construct the high temperature disordered spin configurations. For large  ,
a typical spin configuration is a “frozen” one: A large cluster of same
spins with a few isolated thermal fluctuations of different spins. Most of
the times, the Wolff algorithm picks a seed in the dominant cluster and
the new cluster is almost the same as the dominant cluster: Most of its
sites are included with few ones excluded, which upon flipping of the
spins, they will form the new thermal fluctuations. After the flips, the old
thermal fluctuations have the same spin as the dominant cluster and they
become part of the new dominant cluster. The Metropolis algorithm picks
lattice sites randomly: When they belong to the dominant cluster they are
seldomly flipped, whereas the thermal fluctuations are flipped most of the
time. Both algorithms function similarly and have the same efficiency.
,
a typical spin configuration is a “frozen” one: A large cluster of same
spins with a few isolated thermal fluctuations of different spins. Most of
the times, the Wolff algorithm picks a seed in the dominant cluster and
the new cluster is almost the same as the dominant cluster: Most of its
sites are included with few ones excluded, which upon flipping of the
spins, they will form the new thermal fluctuations. After the flips, the old
thermal fluctuations have the same spin as the dominant cluster and they
become part of the new dominant cluster. The Metropolis algorithm picks
lattice sites randomly: When they belong to the dominant cluster they are
seldomly flipped, whereas the thermal fluctuations are flipped most of the
time. Both algorithms function similarly and have the same efficiency.




 ). In
contrast, the Metropolis algorithm modifies clusters by slowly moving their
boundaries and large clusters are destroyed/created very slowly. Autocorrelation
times are expected to reduce drastically when using the Wolff algorithm in the
critical region.
). In
contrast, the Metropolis algorithm modifies clusters by slowly moving their
boundaries and large clusters are destroyed/created very slowly. Autocorrelation
times are expected to reduce drastically when using the Wolff algorithm in the
critical region.
 ) we have
that
) we have
that

 . In the end, the lattice will be divided in
. In the end, the lattice will be divided in  Wolff
Wolff sites, whose spin is
sites, whose spin is  . Choose a lattice site
randomly and flip the spins of the cluster it belongs to. Destroy the bonds and repeat the
process
. Choose a lattice site
randomly and flip the spins of the cluster it belongs to. Destroy the bonds and repeat the
process

 are equally probable due to the symmetry of the model,
therefore the first term vanishes. Since
are equally probable due to the symmetry of the model,
therefore the first term vanishes. Since  , we obtain
, we obtain

 is
is


 we have that
we have that



 .
.

 . The new members of
the cluster are pushed into the stack
. The new members of
the cluster are pushed into the stack 
 (it has been set in
(it has been set in  ), then we add
), then we add  is defined in
is defined in  ,
,  , by constructing 5000 clusters, starting from a
hot configuration and writing the data to the file
, by constructing 5000 clusters, starting from a
hot configuration and writing the data to the file  , we have to
perform simulations for many values of
, we have to
perform simulations for many values of  . Then, we want to study the finite
size properties and extrapolate the results to the thermodynamic limit,
by repeating the process for several values of
. Then, we want to study the finite
size properties and extrapolate the results to the thermodynamic limit,
by repeating the process for several values of  . The process is long
and ... boring. Moreover, a bored researcher makes mistakes and several
bugs can enter into her calculations. Laziness is a virtue in this case and
it is worth the trouble and the time investment in order to learn some
techniques that will make our life easier, our work more efficient, and
our results more reliable. Shell scripting can be used in order to code
repeated tasks of the command line. In its simplest form, it is just a series of
commands written into a text file. Such an example can be found in the file
. The process is long
and ... boring. Moreover, a bored researcher makes mistakes and several
bugs can enter into her calculations. Laziness is a virtue in this case and
it is worth the trouble and the time investment in order to learn some
techniques that will make our life easier, our work more efficient, and
our results more reliable. Shell scripting can be used in order to code
repeated tasks of the command line. In its simplest form, it is just a series of
commands written into a text file. Such an example can be found in the file
 (
( –
–  . Each
simulation starts from the configuration stored in the file
. Each
simulation starts from the configuration stored in the file  ,
,  , ... ,
, ... ,  , each time with
, each time with  and
and
 .
.
 and the
magnetization per site
and the
magnetization per site  with their errors can be calculated by the
jackknife program, which can be found in the file
with their errors can be calculated by the
jackknife program, which can be found in the file  can be
calculated using the command:
can be
calculated using the command:
 . The condition
. The condition
 and its error and then the fluctuations
and its error and then the fluctuations  and their error.
The latter must be multiplied by
and their error.
The latter must be multiplied by  , in order to obtain the specific
heat
, in order to obtain the specific
heat  and its error according to (
and its error according to ( and/or
and/or  , by editing the values of the variables
, by editing the values of the variables  and
and  .
.
 .
The result is
.
The result is
 and
and  .
.
 :
:
 .
.














 .
.



 –dependent unit of time equal to one Wolff
cluster update. We use the notation
–dependent unit of time equal to one Wolff
cluster update. We use the notation  when the autocorrelation time of
when the autocorrelation time of  is
measured in Wolf cluster updates, and
is
measured in Wolf cluster updates, and  when using the definition (
when using the definition (
 and
and  at
at
 using the Wolff algorithm. We construct
using the Wolff algorithm. We construct  Wolff clusters. The
results are written to files with names
Wolff clusters. The
results are written to files with names  sweeps. The results are
written to files with names
sweeps. The results are
written to files with names  :
:
 sweeps for thermalization. The results are
written to files whose names have file extension
sweeps for thermalization. The results are
written to files whose names have file extension  is fitted to (
is fitted to (








 where
where  is the dynamic exponent
is the dynamic exponent can be calculated by the
can be calculated by the  is calculated for the Wolff algorithm in Wolff steps and Wolff
sweeps. The results are
is calculated for the Wolff algorithm in Wolff steps and Wolff
sweeps. The results are



















 reported in the
bibliography are
reported in the
bibliography are  ,
,  and
and  respectively
respectively  , (
, ( ,
and (
,
and ( and using
and using  , valid in the critical region, we
obtain
, valid in the critical region, we
obtain

 ,
,  and
and  . Therefore
. Therefore

 ,
,  , we obtain
, we obtain























































 ,
,  and
and  . The result is that, although
using them it is possible to compute correct results, these relations are not the best
choice
. The result is that, although
using them it is possible to compute correct results, these relations are not the best
choice and large
and large  . The results depend strongly on the choice of range of the data included
in the fits. The systematic errors are large and the results in some cases plain
wrong
. The results depend strongly on the choice of range of the data included
in the fits. The systematic errors are large and the results in some cases plain
wrong ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 and
and  . The temperatures chosen correspond to small enough
. The temperatures chosen correspond to small enough  in order
to observe scaling. For the values of
in order
to observe scaling. For the values of  used in the simulations, see the shell
scripts in the accompanying software.
used in the simulations, see the shell
scripts in the accompanying software.
 from the relation (
from the relation ( , we fit the data for
, we fit the data for  for an appropriate range of
for an appropriate range of  to
the function
to
the function  , which has two fitting parameters,
, which has two fitting parameters,  and
and  . We
determine the range of
. We
determine the range of  where
where  gives a linear plot in a log–log
scale
gives a linear plot in a log–log
scale , we observe deviations from the linear behavior and for very small
, we observe deviations from the linear behavior and for very small
 we observe finite size effects when
we observe finite size effects when  . As
. As  increases, finite size effects
decrease, and the data get closer to the asymptotic behavior
increases, finite size effects
decrease, and the data get closer to the asymptotic behavior  for even
smaller
for even
smaller  . The results are more clear for
. The results are more clear for  , because for
, because for  the
fluctuations near the pseudocritical temperature
the
fluctuations near the pseudocritical temperature  are larger and the
finite size effects are larger.
are larger and the
finite size effects are larger.
 for all the measured values of
for all the measured values of
 . The errors reported are the statistical errors of the fits, which are smaller
than the systematic errors coming from the choice or range of
. The errors reported are the statistical errors of the fits, which are smaller
than the systematic errors coming from the choice or range of  of the data
included in the fits. One has to vary this range as long as the
of the data
included in the fits. One has to vary this range as long as the  dof of the fit
remains acceptable, and the resulting variation in the values of the parameters has
to be included in the estimate of the error. Sometimes, this method gives an
overestimated error, and it is a matter or experience to decide which parameter
values to include in the estimate. For example, figures
dof of the fit
remains acceptable, and the resulting variation in the values of the parameters has
to be included in the estimate of the error. Sometimes, this method gives an
overestimated error, and it is a matter or experience to decide which parameter
values to include in the estimate. For example, figures  for
increasing
for
increasing  . As
. As  increases, the points approach the asymptotic curve
even closer. Even though for fixed
increases, the points approach the asymptotic curve
even closer. Even though for fixed  one obtains acceptable power fits
over a larger range of
one obtains acceptable power fits
over a larger range of  , by studying the large
, by studying the large  convergence, we can
determine the scaling region with higher accuracy. Another point to consider is
whether the parameters of the fits have reasonable values. For example, even
though the value of
convergence, we can
determine the scaling region with higher accuracy. Another point to consider is
whether the parameters of the fits have reasonable values. For example, even
though the value of  is unknown, it is reasonable to expect that its
value is of order
is unknown, it is reasonable to expect that its
value is of order  . By taking all these remarks into consideration we
obtain
. By taking all these remarks into consideration we
obtain


 using relation (
using relation ( or
or  . In the thermodynamic limit, the magnetization is everywhere zero for
all
. In the thermodynamic limit, the magnetization is everywhere zero for
all  . For a finite lattice
. For a finite lattice  , and it is reasonable to expect a scaling
of the form
, and it is reasonable to expect a scaling
of the form

 is defined so that
is defined so that

 and
and  shown in table
shown in table 

 .
.
 needs special care. The expected
value is
needs special care. The expected
value is 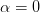 . This does not imply that
. This does not imply that  const. but that
const. but that

 plot. We see that the second choice leads to a
better linear plot than the first one. A careful study will compute the quality of
the fits and choose the better model this way. This is left as an exercise for the
reader.
plot. We see that the second choice leads to a
better linear plot than the first one. A careful study will compute the quality of
the fits and choose the better model this way. This is left as an exercise for the
reader.

















 ,
,  and
and
 with increasing system size
with increasing system size  . This is called “finite size
scaling”.
. This is called “finite size
scaling”.
 given by equation (
given by equation ( for increasing values of
for increasing values of  .
We fit the results
.
We fit the results  to the function
to the function  and calculate the fitting
parameters
and calculate the fitting
parameters  and
and  . Then, we compare the computed value of
. Then, we compare the computed value of  to
the expected value of
to
the expected value of  . In this procedure we have to
decide which values of
. In this procedure we have to
decide which values of  should be included in the fits. The most obvious
criterion is to obtain reasonable
should be included in the fits. The most obvious
criterion is to obtain reasonable  and that the error in
and that the error in  and
and
 be small. This is not enough: Table
be small. This is not enough: Table  , if we consider different fit ranges. These
variations give an estimate of the systematic error which enters in the
calculation. Problem
, if we consider different fit ranges. These
variations give an estimate of the systematic error which enters in the
calculation. Problem 
 given by equation (
given by equation ( at the critical temperature and repeat the
same analysis. The result is
at the critical temperature and repeat the
same analysis. The result is

 . But the expected value
. But the expected value  leads, in analogy with equation (
leads, in analogy with equation (
 and appreciate the difficulties
that arise in this study. By increasing the statistics, and by measuring for
larger
and appreciate the difficulties
that arise in this study. By increasing the statistics, and by measuring for
larger  , the data in table
, the data in table 


















































 and
and  in the critical region.
In the calculations we used the exact value of the critical temperature
in the critical region.
In the calculations we used the exact value of the critical temperature
 . When
. When  is not known, the analysis becomes harder and
its computation contributes to the total error in the value of the critical
exponents. When doing finite size scaling using the scaling relations (
is not known, the analysis becomes harder and
its computation contributes to the total error in the value of the critical
exponents. When doing finite size scaling using the scaling relations ( . What should we do
when
. What should we do
when  is not a priori known? A good choice is to use the pseudocritical
temperature
is not a priori known? A good choice is to use the pseudocritical
temperature  , the temperature where the fluctuations of the order
parameter
, the temperature where the fluctuations of the order
parameter  are at their maximum. Otherwise, we can compute
are at their maximum. Otherwise, we can compute  according to the discussion in this section and use the computed
according to the discussion in this section and use the computed  in the finite
size scaling analysis.
in the finite
size scaling analysis.
 limit, even though the
finite size effects are different. In fact any value of
limit, even though the
finite size effects are different. In fact any value of  in the critical region can be
used for this calculation. The reason is that as we approach the critical region for
given
in the critical region can be
used for this calculation. The reason is that as we approach the critical region for
given  , the correlation length becomes
, the correlation length becomes  and finite size effects become
important. This is the behavior that characterizes the
and finite size effects become
important. This is the behavior that characterizes the  system. The pseudocritical region becomes narrower as
system. The pseudocritical region becomes narrower as  becomes
larger. Any value of
becomes
larger. Any value of  in this region will give us observables that scale at large
in this region will give us observables that scale at large
 , but the best choice is
, but the best choice is

 .
.
 in not unique. One could use, for example, the
maximum of the specific heat
in not unique. One could use, for example, the
maximum of the specific heat

 . Of course
. Of course 

 and both choices will yield the same results for large
and both choices will yield the same results for large  . The speed of
convergence and the errors involved in the calculation of the pseudocritical
temperatures are different in each case and there is a preferred choice, which in
our case is
. The speed of
convergence and the errors involved in the calculation of the pseudocritical
temperatures are different in each case and there is a preferred choice, which in
our case is  .
.
 . When we are in the pseudocritical region we have that
. When we are in the pseudocritical region we have that
 , therefore (
, therefore (
 we determine the pseudocritical region and
we calculate
we determine the pseudocritical region and
we calculate  and the corresponding maximum value
and the corresponding maximum value  . In
order to do that, we should take many measurements around
. In
order to do that, we should take many measurements around  . We
have to be very careful in determining the autocorrelation time (which
increases as
. We
have to be very careful in determining the autocorrelation time (which
increases as  ), so that we can control the number of independent
measurements and the thermalization of the system. We use the relation
(
), so that we can control the number of independent
measurements and the thermalization of the system. We use the relation
( , and from the calculated parameters
, and from the calculated parameters
 and
and  we compute
we compute 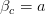 ,
,  . In cases where one of the
parameters
. In cases where one of the
parameters  ,
,  is known independently, then it is kept constant during the
fit.
is known independently, then it is kept constant during the
fit.

 and
and
 .
.
 and the
maximum values of the specific heat
and the
maximum values of the specific heat  . The results are shown in figure
. The results are shown in figure 
 we can calculate the
exponent
we can calculate the
exponent  . Their values are shown in table
. Their values are shown in table  ,
according to the asymptotic relation (
,
according to the asymptotic relation ( and
and 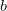 being fitting
parameters. We find very good scaling, therefore our data are in the asymptotic
region. The result is
being fitting
parameters. We find very good scaling, therefore our data are in the asymptotic
region. The result is

 .
.
 .
Since
.
Since  , the form of the asymptotic behavior is given by (
, the form of the asymptotic behavior is given by ( and it is possible
that the discrepancy is due to finite size effects. We add terms that are subleading
in
and it is possible
that the discrepancy is due to finite size effects. We add terms that are subleading
in  and find that the fit to the function
and find that the fit to the function  is very
good
is very
good , the quality of the fit
is poor and the result for
, the quality of the fit
is poor and the result for  is consistent with zero. The results are shown in
figure
is consistent with zero. The results are shown in
figure 
















 . As we approach the critical point,
. As we approach the critical point,  diverges as
diverges as  , and we obtain
universal behavior for all systems in the same universality class. If we consider the
magnetic susceptibility
, and we obtain
universal behavior for all systems in the same universality class. If we consider the
magnetic susceptibility  , its values depend both on the temperature
, its values depend both on the temperature  ,
the size of the system
,
the size of the system  and of course on the details of the system’s degrees of
freedom and their dynamics. Universality leads to the
and of course on the details of the system’s degrees of
freedom and their dynamics. Universality leads to the 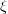 . For the finite system in the pseudocritical region, finite
size effects suppress the fluctuations when
. For the finite system in the pseudocritical region, finite
size effects suppress the fluctuations when  . The length scales
that determine the dominant scaling behavior
. The length scales
that determine the dominant scaling behavior  are
are  and
and  ,
therefore the
,
therefore the  is the only independent variable in
the scaling functions. In order to obtain the scaling relation
is the only independent variable in
the scaling functions. In order to obtain the scaling relation  ,
valid for the infinite system, we only need to assume that for the finite
system
,
valid for the infinite system, we only need to assume that for the finite
system
 is a function of
is a function of 

 (
( ) the magnetic susceptibility takes values very
close to those of the infinite system, and (
) the magnetic susceptibility takes values very
close to those of the infinite system, and ( . As
. As  ,
finite size effects enter and (
,
finite size effects enter and ( . The latter is
nothing but (
. The latter is
nothing but ( describes
how the magnetic susceptibility deviates from scaling due to finite size
effects.
describes
how the magnetic susceptibility deviates from scaling due to finite size
effects.
 can be calculated using the measurements coming from
the Monte Carlo simulation. Since the correlation length is not directly calculated,
but appears indirectly in the measurements, we define the dimensionless
variable
can be calculated using the measurements coming from
the Monte Carlo simulation. Since the correlation length is not directly calculated,
but appears indirectly in the measurements, we define the dimensionless
variable

 since
since . We define
. We define  so that (
so that (
 are determined by the
relations (
are determined by the
relations ( , equation (
, equation ( and we obtain
and we obtain  From the definition
From the definition
 we obtain
we obtain  and we confirm the
scaling property of the magnetic susceptibility in the thermodynamic limit
and we confirm the
scaling property of the magnetic susceptibility in the thermodynamic limit
 . Therefore
. Therefore

 , (
, ( .
Then we obtain
.
Then we obtain  Therefore, we
confirm that, when finite size effects are dominant (
Therefore, we
confirm that, when finite size effects are dominant ( ), we have that
), we have that
 . Therefore
. Therefore


 are measurements for temperatures in the pseudocritical
region for several values of
are measurements for temperatures in the pseudocritical
region for several values of  . When equation (
. When equation ( independently of
the size
independently of
the size  ! Of course deviations due to finite size effects are expected,
especially when
! Of course deviations due to finite size effects are expected,
especially when  is small. But, as we will see, convergence is quite
fast.
is small. But, as we will see, convergence is quite
fast.
 , the
exponent
, the
exponent  and the ratio
and the ratio  simultaneously! In order to check (
simultaneously! In order to check ( , for which it is necessary to
know
, for which it is necessary to
know  (
( ) and the exponent
) and the exponent  . For the calculation of
. For the calculation of
 it is necessary to know
it is necessary to know  that appears on the right hand side of
(
that appears on the right hand side of
( ,
,  and
and  and this way we obtain an accurate method for their
calculation.
and this way we obtain an accurate method for their
calculation.
 . Using
. Using  ,
,  ,
,  and
and  , we calculate the scaling variable
, we calculate the scaling variable
 . Using
. Using  and
and  , we calculate
, we calculate
 and plot the points
and plot the points  near the critical region
near the critical region
 . Then we vary
. Then we vary  until the curves for different
until the curves for different  collapse onto
each other. The optimal collapse determines
collapse onto
each other. The optimal collapse determines  .
.
 for different
for different  is the most efficient
method for studying scaling in the critical region. Figure
is the most efficient
method for studying scaling in the critical region. Figure  for the known values of the parameters
for the known values of the parameters 
 . Small variations of the parameters lead to a sharp change
of the quality of the collapse. We can make a quick and dirty estimate of the
accuracy of the method by varying
. Small variations of the parameters lead to a sharp change
of the quality of the collapse. We can make a quick and dirty estimate of the
accuracy of the method by varying 


 . The results are shown in figures
. The results are shown in figures  whereas the ones starting with
whereas the ones starting with  . The program can
be found in the file
. The program can
be found in the file  separated
from another by one or more spaces. The variables
separated
from another by one or more spaces. The variables  ,
,  and
and  that will be used in the scaling relation (
that will be used in the scaling relation ( (the index
(the index 
 and its
error
and its
error  ). For
). For  , the
, the  bins and work
independently on each set of data. Each bin will give an optimal set of
parameters
bins and work
independently on each set of data. Each bin will give an optimal set of
parameters  which will be assumed to be an independent
measurement. The errors can be calculated using equation (
which will be assumed to be an independent
measurement. The errors can be calculated using equation ( ).
).
 similar to the one used in data fitting, as discussed in appendix
similar to the one used in data fitting, as discussed in appendix
 should increase. Assume that our measurements consist of
should increase. Assume that our measurements consist of  sets of
measurements for
sets of
measurements for  . After setting the parameters
. After setting the parameters
 and an interval
and an interval ![Δx ≡ [x ,x ]
min max](main_latex5931x.png) , we calculate the data sets
, we calculate the data sets
 , for all
, for all  , using our measurements.
The data sets consist of
, using our measurements.
The data sets consist of  points of the data for
points of the data for  , for which
the
, for which
the  are in the interval
are in the interval  . For each point
. For each point  , we calculate the
scaling function
, we calculate the
scaling function  , which depends on the
chosen parameters
, which depends on the
chosen parameters  and the lattice size
and the lattice size  . Then, we have to choose
an interpolation method, which will define the interpolation
. Then, we have to choose
an interpolation method, which will define the interpolation 
 in a data set has a well defined distance
from every other data set
in a data set has a well defined distance
from every other data set  (
( and
and  ), which is defined by the
distance from the interpolating function of the other sets. This is equal
to
), which is defined by the
distance from the interpolating function of the other sets. This is equal
to . We define the quantity
. We define the quantity 
 is the number of terms in the sum. The normalization
constant
is the number of terms in the sum. The normalization
constant  is used, because this is the number of pairs of curves in the
sum. Each term is weighted by its error
is used, because this is the number of pairs of curves in the
sum. Each term is weighted by its error  , so that points with
small error have a larger contribution than points with large error. This is
the definition used in
, so that points with
small error have a larger contribution than points with large error. This is
the definition used in  depends on the parameters
depends on the parameters  and the interval
and the interval  . Initially,
we keep
. Initially,
we keep  fixed and perform a minimization with respect to the parameters
fixed and perform a minimization with respect to the parameters
 . The minimum is given by the values
. The minimum is given by the values  and these values are the
estimators that we are looking for. In order to calculate the errors
and these values are the
estimators that we are looking for. In order to calculate the errors  we can bin
our data according to the discussion on page
we can bin
our data according to the discussion on page  distribution of the measurements, and if the minimum
distribution of the measurements, and if the minimum  , then the
intervals of the parameter values that keep
, then the
intervals of the parameter values that keep  give an estimate of the errors
in the parameters.
give an estimate of the errors
in the parameters.
 . Usually
. Usually  so that
so that ![Δx = [xmax − δx, xmax + δx]](main_latex5966x.png) . If
. If
 is larger than it should, then
is larger than it should, then  is large and we don’t have good
scaling. If it is too small, then the errors
is large and we don’t have good
scaling. If it is too small, then the errors  will be large. By taking the limit
will be large. By taking the limit
 , we calculate
, we calculate  by studying the convergence of
by studying the convergence of  to stable, optimal
with respect to error, values (see figure 8.7, page 238 in
to stable, optimal
with respect to error, values (see figure 8.7, page 238 in 


 corresponds to the Gaussian distribution, whereas the value
corresponds to the Gaussian distribution, whereas the value  corresponds to two Gaussian distributions of small width around two symmetric
values
corresponds to two Gaussian distributions of small width around two symmetric
values  (see problems
(see problems  are small,
therefore the calculation of
are small,
therefore the calculation of  gives an accurate measurement of
the critical temperature
gives an accurate measurement of
the critical temperature  . The curves
. The curves  intersect at the point
(
intersect at the point
( ,
,  ) for different
) for different  and this point gives a very good estimate of
and this point gives a very good estimate of
 .
.












 . The intersection of the
curves in the figure at a single point (
. The intersection of the
curves in the figure at a single point ( ,
,  ) is impressively accurate. Table
) is impressively accurate. Table
 systematically by computing the critical
temperature from the intersection of the curves
systematically by computing the critical
temperature from the intersection of the curves  for three values of
for three values of  .
By taking into account all the measurements for
.
By taking into account all the measurements for  –
–  the computed
result is
the computed
result is

 ,
,
 . Notice that, in the calculation of
. Notice that, in the calculation of  the systematic error
due to finite size effects decreases with increasing
the systematic error
due to finite size effects decreases with increasing  , whereas the statistical error
increases due to the increase of the slope of the curves
, whereas the statistical error
increases due to the increase of the slope of the curves  near the point
near the point
 . But the accuracy of the calculation of
. But the accuracy of the calculation of  turns out to be better with
increasing
turns out to be better with
increasing  .
.





 and
and  . From equation (
. From equation ( scales as
scales as

 , we obtain
, we obtain
 , which is consistent with the result (
, which is consistent with the result ( , can be
hard in the general case. Therefore it is desirable to cross check results using
several observables which have known scaling behavior. We discuss some of them
below
, can be
hard in the general case. Therefore it is desirable to cross check results using
several observables which have known scaling behavior. We discuss some of them
below






 defines a pseudocritical region
around its maximum. The scaling of the maximum as well as the scaling of its
position can be used in order to compute
defines a pseudocritical region
around its maximum. The scaling of the maximum as well as the scaling of its
position can be used in order to compute  , as we did in figures
, as we did in figures 





















 ,
whereas for a first order phase transition, we obtain a non trivial value. Therefore,
this parameter can be used in order to determine whereas a system undergoes a
first order phase transition. This is confirmed in figure
,
whereas for a first order phase transition, we obtain a non trivial value. Therefore,
this parameter can be used in order to determine whereas a system undergoes a
first order phase transition. This is confirmed in figure  converge to the critical temperature according to (
converge to the critical temperature according to (
 and its derivatives. For more
details, the reader is referred to
and its derivatives. For more
details, the reader is referred to  are trivial in two cases: When the magnetization follows a
Gaussian distribution, which is true in the high temperature, disordered phase, we
have that
are trivial in two cases: When the magnetization follows a
Gaussian distribution, which is true in the high temperature, disordered phase, we
have that  . When we are in the low temperature, ordered phase, we have
that
. When we are in the low temperature, ordered phase, we have
that  . The proof is easy and it is left as an exercise (see problems
. The proof is easy and it is left as an exercise (see problems  of a continuum phase transition is approached, the system exhibits scaling
properties due to the diverging correlation length
of a continuum phase transition is approached, the system exhibits scaling
properties due to the diverging correlation length  . If we approach
. If we approach  from the
high temperature phase, then we expect that the distribution function of the
magnetization per site
from the
high temperature phase, then we expect that the distribution function of the
magnetization per site  (not its absolute value) is approximately of the
form
(not its absolute value) is approximately of the
form



 . We have
temporarily assumed that the system is defined on a
. We have
temporarily assumed that the system is defined on a  –dimensional hypercubic
lattice of edge
–dimensional hypercubic
lattice of edge  .
.
 scales according to the relation
scales according to the relation 


 ,
,  , is the correlation
length
, is the correlation
length  , in such a way that
, in such a way that  . Equation (
. Equation (
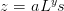 . For the left hand side to be equal to one, we must have
that
. For the left hand side to be equal to one, we must have
that  ,
,

 .
.  ,
,  and
and  is a constant
independent of
is a constant
independent of  and
and  . Finally, we obtain
. Finally, we obtain

 are
are 
 . When we
. When we  and
and  , the correlation length
, the correlation length  diverges in such a way that
diverges in such a way that  .
In the region
.
In the region  (
( ) we have that
) we have that  , and by using the
relations
, and by using the
relations


 and
and  ,
which are universal constants (i.e. they are the same within a universality class)
and they are defined from equation (
,
which are universal constants (i.e. they are the same within a universality class)
and they are defined from equation ( on the right and left hand
sides
on the right and left hand
sides
 -scaling, we substitute the above equations to (
-scaling, we substitute the above equations to ( , and we obtain
, and we obtain



 ,
,



 . From equation (
. From equation (
 keeping
keeping  finite, and the
fluctuations get suppressed, rendering the functions
finite, and the
fluctuations get suppressed, rendering the functions  finite. Therefore, we
obtain
finite. Therefore, we
obtain
 at the critical temperature turned out to be
almost independent of the system size
at the critical temperature turned out to be
almost independent of the system size  .
.  is found to depend on the
boundary conditions and on the anisotropy of the interaction. For the Ising model
on the square lattice we have that
is found to depend on the
boundary conditions and on the anisotropy of the interaction. For the Ising model
on the square lattice we have that 

 is the dimensionless correlation length in the thermodynamic
limit and
is the dimensionless correlation length in the thermodynamic
limit and  is the scaling factor
is the scaling factor
 is the reduced temperature and
is the reduced temperature and  is the external magnetic
field
is the external magnetic
field and
and  give the change in the coupling constants
give the change in the coupling constants  and
and
 under the change in length scale in order that the equation remains
valid.
under the change in length scale in order that the equation remains
valid.
 times we obtain
times we obtain

 ,
,  , keeping the product
, keeping the product 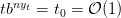 fixed, we
obtain
fixed, we
obtain 
 and
and  and the
critical exponent
and the
critical exponent


 ,
,  , keeping the product
, keeping the product  , the left
hand side will give a finite value, e.g.
, the left
hand side will give a finite value, e.g.  whereas the right hand side will
give
whereas the right hand side will
give

 , and by comparing to the known relation (
, and by comparing to the known relation ( , we obtain
, we obtain


 whenever we neglect terms that are not related to the
scaling properties of a function.
whenever we neglect terms that are not related to the
scaling properties of a function.
 , we obtain the
specific heat
, we obtain the
specific heat
 is nothing but the critical exponent of the
specific heat defined in equation (
is nothing but the critical exponent of the
specific heat defined in equation (

 we obtain the
magnetic susceptibility
we obtain the
magnetic susceptibility

 , we obtain
, we obtain


 (the volume is
(the volume is  ,
,  is the number of
dimensions), where
is the number of
dimensions), where  is the (dimensionless) number of lattice sites and
is the (dimensionless) number of lattice sites and  is the
lattice constant. We consider the limit
is the
lattice constant. We consider the limit  and
and  , so that
, so that 
 -scale
-scale



 ,
,  and
and 

 (approach of the critical point), the above relation becomes
(approach of the critical point), the above relation becomes

 as in the previous section we
obtain
as in the previous section we
obtain
 ,
, 
 .
.
 where
where  ,
which yields the known relation
,
which yields the known relation  .
.
 is comparable to
is comparable to  , finite size effects dominate. The large
fluctuations are suppressed and the magnetic susceptibility has a maximum at
a crossover (pseudocritical) temperature
, finite size effects dominate. The large
fluctuations are suppressed and the magnetic susceptibility has a maximum at
a crossover (pseudocritical) temperature 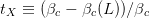 , where
, where
 . The last relation holds because
. The last relation holds because  by assumption. We
obtain
by assumption. We
obtain


 is analytic in its
argument
is analytic in its
argument  , since for a finite system
, since for a finite system  is an analytic function of the
temperature
is an analytic function of the
temperature and
and  , therefore
, therefore  )
)



 . Near the
pseudocritical point
. Near the
pseudocritical point

 we have that
we have that

 (equation (
(equation (
 . This
increases the pseudocritical temperature
. This
increases the pseudocritical temperature  (
(
 in (
in ( (
(
 in (
in ( (
(
 in (
in ( depends on the boundary conditions and the geometry
of the lattice.
depends on the boundary conditions and the geometry
of the lattice.



 for
small
for
small  . Then, we see that
. Then, we see that


 . The term
proportional to
. The term
proportional to  vanishes when we set
vanishes when we set  . In the pseudocritical region,
where
. In the pseudocritical region,
where  , the first and third term are of the same order in
, the first and third term are of the same order in  and we
obtain
and we
obtain








 ,
,  . The relation
. The relation

 coming from the two point correlation function
coming from the two point correlation function
 .
.





















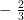











































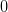





















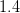




















 for the Metropolis algorithm
as a function of the temperature for
for the Metropolis algorithm
as a function of the temperature for  ,
,  ,
,  . Compute
the average size
. Compute
the average size  of the Wolff clusters at the same values of the
temperatures. Then calculate the number of Wolff clusters that are
equivalent to a Metropolis sweep. Make the plots of all of your results
and connect the points corresponding to the same
of the Wolff clusters at the same values of the
temperatures. Then calculate the number of Wolff clusters that are
equivalent to a Metropolis sweep. Make the plots of all of your results
and connect the points corresponding to the same  .
.  ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
 ,
,  ,
,
 ,
,  ,
,  ,
,  . Recalculate the dynamic exponent
. Recalculate the dynamic exponent  using
your data.
using
your data.
 ,
,  ,
,  ,
,  .
Recalculate the dynamic exponent
.
Recalculate the dynamic exponent  using your data.
using your data.

 , where
, where  is the average acceptance
ratio of the Metropolis algorithm. This changes the unit of time to
is the average acceptance
ratio of the Metropolis algorithm. This changes the unit of time to 
 .
.
 ,
,  ,
,
 ,
,  ,
,  . Choose appropriate values of
. Choose appropriate values of  , so that you will be
able to determine the magnetic susceptibility and the specific heat with
an accuracy comparable to the one shown in table
, so that you will be
able to determine the magnetic susceptibility and the specific heat with
an accuracy comparable to the one shown in table  and
and  by
computing the
by
computing the  according to the discussion in appendix
according to the discussion in appendix  ,
, and
and  . Use the values in this table in order to make the
fits which give the exponents
. Use the values in this table in order to make the
fits which give the exponents  ,
,  and
and  as described in the
text. For the exponent
as described in the
text. For the exponent  , try fitting to a power and a logarithm
and compare the results according to the discussion in the text.
, try fitting to a power and a logarithm
and compare the results according to the discussion in the text.








 ,
,
 ,
,  ,
,  and
and  . Make the appropriate fits in order to
calculate the exponents
. Make the appropriate fits in order to
calculate the exponents  ,
,  ,
,  and the critical temperature
and the critical temperature  as described in the text. For the exponent
as described in the text. For the exponent  , try fitting to a power and a
logarithm and compare the results according to the discussion in the
text.
, try fitting to a power and a
logarithm and compare the results according to the discussion in the
text.
 . Vary each parameter separately, so that the collapse becomes
not satisfactory and use its variation as an estimate of its error.
Determine the range in
. Vary each parameter separately, so that the collapse becomes
not satisfactory and use its variation as an estimate of its error.
Determine the range in  that gives satisfactory collapse of the
curves. Repeat your calculation by performing measurements for
that gives satisfactory collapse of the
curves. Repeat your calculation by performing measurements for
 , and using the data for
, and using the data for  . Compare the
new results with the previous ones and comment on the finite size
effects.
. Compare the
new results with the previous ones and comment on the finite size
effects.
 we have that
we have that 

 . Using this relation
calculate the derivative of the Binder cumulant
. Using this relation
calculate the derivative of the Binder cumulant  and prove equation
(
and prove equation
( in order to
calculate the critical exponent
in order to
calculate the critical exponent 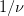 according to the analysis shown in
figures
according to the analysis shown in
figures  we have that
we have that
 and
and  . Conclude that
. Conclude that  .
.

 . Show that
. Show that  and
and  .
Interpret your results, i.e. the meaning of each expectation value. Show
that for
.
Interpret your results, i.e. the meaning of each expectation value. Show
that for  we obtain
we obtain  . Convince yourself that the
approximation used concerns the system in the low temperature
phase.
. Convince yourself that the
approximation used concerns the system in the low temperature
phase.
 as a function of
as a function of  ,
,  ,
,  and
and  . Apply finite size scaling arguments and prove equation (
. Apply finite size scaling arguments and prove equation ( ,
,  in order to prove
the other relations in (
in order to prove
the other relations in ( ,
,  dof,
dof,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  dof,
dof,  symmetry,
symmetry,  ,
,  cycles,
cycles,