Calculates LP coefficients from the autocorrelation coefficients.
Syntax
IppStatus ippsLevinsonDurbin_G729_32s16s(const Ipp32s* pSrcAutoCorr, int order, Ipp16s* pDstLPC, Ipp16s* pDstRc, Ipp16s* pResultResidualEnergy);
IppStatus ippsLevinsonDurbin_G729_32f(const Ipp32f* pSrcAutoCorr, int order, Ipp32f* pDstLpc, Ipp32f* pDstRc, Ipp32f* pResultResidualEnergy);
IppStatus ippsLevinsonDurbin_G729B(const Ipp32s* pSrcAutoCorr, Ipp16s* pDstLPC, Ipp16s* pDstRC, Ipp16s* pResultResidualEnergy);
Parameters
order |
The LP order. |
pSrcAutoCorr |
Pointer to the autocorrelation coefficients vector [order +1]. |
pDstLPC |
Pointer to the output LP coefficients [order+1]. |
pDstRC |
Pointer to the output reflection coefficients vector [order]. |
pResultResidualEnergy |
Pointer to the residual energy. |
Description
The functions ippsLevinsonDurbin_G729 and ippsLevinsonDurbin_G729B are declared in the ippsc.h file. These functions calculate Linear Prediction (LP) coefficients of the LP filter with the given order from the autocorrelation coefficients, using Levinson-Durbin algorithm. The function ippsLevinsonDurbin_G729uses the parameter order, while the function ippsLevinsonDurbin_G729B operates for the default order = 10.
To obtain LP coefficients ai, i = 1, 2, ..., order, the following set of equations is to be solved:
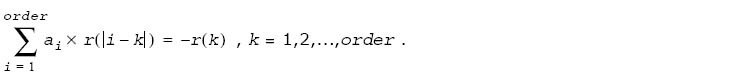
,
k = 1,2,...,order .
The functions perform the following steps:
1. Levinson-Durbin algorithm is applied to solve the above set of equations. This algorithm uses the following recursion.
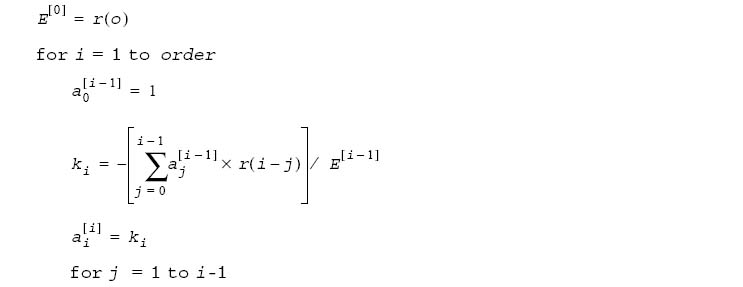
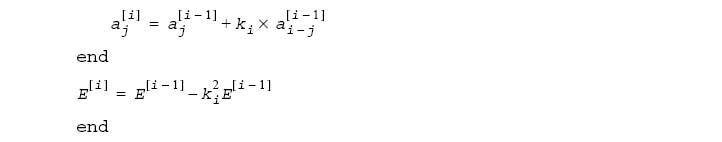
2. Set E as the output residual energy and ki as reflection coefficients.
3. If the LPC filter used in this algorithm is unstable, that is some |ki| is very close to 1.0 during recursion, the elements of input vectors pSrcDstLPC and pSrcDstRC RC coefficients are not changed and the residual energy is set to 0.
Return Values
ippStsNoErr |
Indicates no error. |
ippStsNullPtrErr |
Indicates an error when the pSrcAutoCorr, pDstRC, pResultResidualEnergy, or pDstLPC pointer is NULL. |
ippStsSizeErr |
Indicates an error when order is less than or equal to 0, or when order is greater than 30. |