This is the fastest and least accurate interpolation mode. The pixel value in the destination image is set to the value of the source image pixel closest to the point
(xS,yS):D(xD,yD) = S(round(xS), round(yS)).
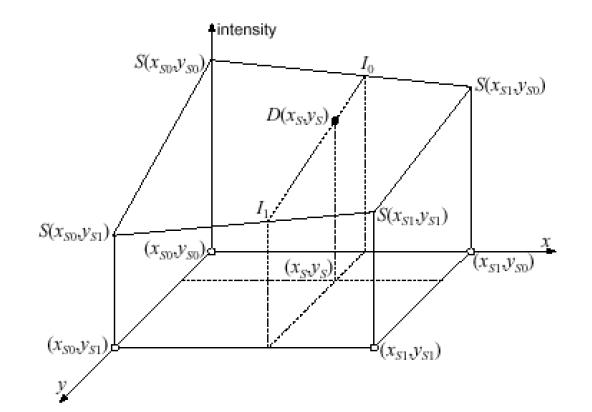
The linear interpolation is slower but more accurate than the nearest neighbor interpolation. On the other hand, it is faster but less accurate than cubic interpolation. The linear interpolation algorithm uses source image intensities at the four pixels (xS0, yS0), (xS1, yS0), (xS0, yS1), (xS1, yS1) that are closest to (xS, yS) in the source image:
xS0 = int(xS), xS1 = xS0 + 1, yS0 = int(yS), yS1 = yS0 + 1.
First, the intensity values are interpolated along the x-axis to produce two intermediate results I0 and I1 (see Figure Linear Interpolation):
I0 = S(xS, yS0) = S(xS0, yS0)*(xS1 - xS) + S(xS1, yS0)*(xS - xS0)
I1 = S(xS, yS1) = S(xS0, yS1)*(xS1 - xS) + S(xS1, yS1)*(xS - xS0).
Then, the sought-for intensity D(xD, yD) is computed by interpolating the intermediate values I0 and I1 along the y-axis:
D(xD, yD) = I0*(yS1 - yS) + I1*(yS - yS0).
To use the linear interpolation, set the parameter interpolation to IPPI_INTER_LINEAR. For images with 8-bit unsigned color channels, the functions ippiWarpAffine, ippiRotate, and ippiShear compute the coordinates (xS, yS) with the accuracy 2-16 = 1/65536. For images with 16-bit unsigned color channels, these functions compute the coordinates with floating-point precision.