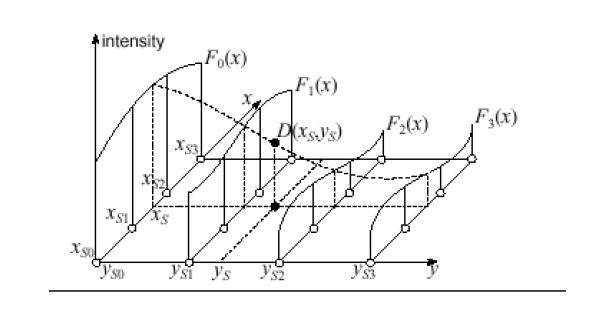
The cubic interpolation algorithm (see Figure Cubic Interpolation) uses source image intensities at sixteen pixels in the neighborhood of the point (xS, yS) in the source image:
xS0 = int(xS) - 1; xS1 = xS0 + 1; xS2 = xS0 + 2; xS3 = xS0 + 3;
yS0 = int(yS) - 1; yS1 = yS0 + 1; yS2 = yS0 + 2;yS3 = yS0 + 3.
First, for each ySk the algorithm determines four cubic polynomials F0(x), F1( x), F2( x), and F3( x):
Fk( x) = akx3 + bkx2 + ckx + dk, 0 ≤ k ≤ 3
such that
F k( xS0) = S(xS0, ySk); Fk(xS1) = S(xS1, ySk),
Fk( xS2) = S(xS2, ySk); Fk( xS3) = S(xS3, ySk).
In Figure Cubic Interpolation , these polynomials are shown by solid curves.
Then, the algorithm determines a cubic polynomial Fy(y) such that
Fy(yS0) = F0( xS), Fy(yS1) = F1(xS), Fy(yS2) = F2(xS), Fy( yS3) = F3( xS).
The polynomial Fy(y) is represented by the dashed curve in Figure Cubic Interpolation.
Finally, the sought intensity D(xD, yD) is set to the value Fy(yS).
To use the linear interpolation, set the parameter interpolation to IPPI_INTER_CUBIC. For images with 8-bit unsigned color channels, the functions ippiWarpAffine, ippiRotate, and ippiShear compute the coordinates (xS, yS) with the accuracy 2-16 = 1/65536. For images with 16-bit unsigned color channels, these functions compute the coordinates with floating-point precision.