Schwarzschild λύση: Παράδειγμα επίλυσης εξισώσεων Einstein

H Schwarzschild λύση αποτελεί μία από τις πιο απλές και χρήσιμες λύσεις των εξισώσεων του Einstein. Περιγράφει τον χωρόχρονο σε ένα  μη περιστρεφόμενο και σφαιρικά συμμετρικό αντικείμενο. Ικανοποιεί τις εξισώσεις Einstein αποτελώντας την πιο γενική στατική και ισοτροπική μετρική στο κενό.

 (1)
Συνεπώς, η μετρική  εκφράζεται σαν συνάρτηση της μεταβλητής  r δηλαδή:.

Από τον τύπο:  έπειτα από πράξεις καταλήγουμε στη σχέση: (2), όπου: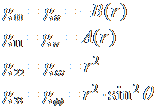

• Στρατηγική Επίλυσης

• Βήμα 1: Εύρεση των συμβόλων Christoffel .

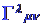Τα σύμβολα Christoffelδίνονται από τον τύπο: 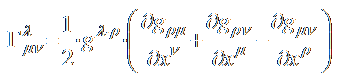(3)

Γνωρίζοντας ότι  

και ότι 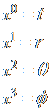 επιλύουμε την παραπάνω εξίσωση για τις διάφορες τιμές των λ, μ, ν (=0,1,2,3).

Ομοίως βρίσκουμε και τα υπόλοιπα. Από τις λύσεις προκύπτουν 13 μη μηδενικές λύσεις 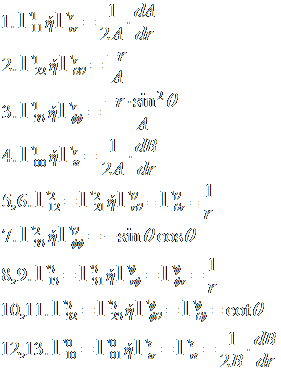(4)

• Βήμα 2: Εύρεση του τανυστή Riemann καμπυλότητας .

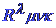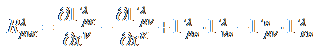Ο τανυστής Riemann καμπυλότητας  δίνεται από τον τύπο:  (5)

• Βήμα 3: Εύρεση του τανυστή Ricci .

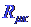O τανυστής Ricci  δίνεται από τη σχέση:  (6)

• Βήμα 4: Εύρεση της καμπυλότητας R (βαθμωτό μέγεθος).

Η καμπυλότητα R δίνεται από τη σχέση: 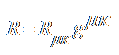(7)

• Βήμα 5: Επίλυση συστήματος 3 εξισώσεων χρησιμοποιώντας την εξίσωση Einstein στο κενό και τους τανυστές Ricci.

Από την εξίσωση του Einstein στο κενό () αρκεί να χρησιμοποιήσουμε την σχέση.

Προκύπτει σύστημα 3 εξισώσεων: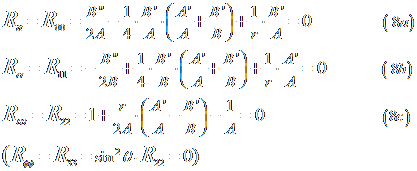

• Μέθοδος Επίλυσης του Συστήματος

Τελικά, αντικαθιστώντας στην αρχική σχέση του τα Α, Β προκύπτει η τελική λύση (1916):

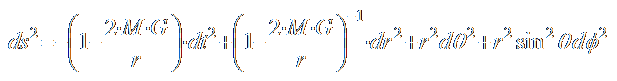(9)

Μηδενίζοντας τον παράγοντα του χρόνου βρίσκουμε την ακτίνα του ορίζοντα γεγονότων της μαύρης τρύπας:  (10)

Ας δούμε τώρα τι μάθαμε...

• Κάνε το ΤΕΣΤ!