?lagv2

Computes the Generalized Schur factorization of a real 2-by-2 matrix pencil (A,B) where B is upper triangular.

Syntax

call slagv2( a, lda, b, ldb, alphar, alphai, beta, csl, snl, csr, snr )

call dlagv2( a, lda, b, ldb, alphar, alphai, beta, csl, snl, csr, snr )

Include Files

mkl.fi

Description

The routine computes the Generalized Schur factorization of a real 2-by-2 matrix pencil (A,B) where B is upper triangular. The routine computes orthogonal (rotation) matrices given by csl, snl and csr, snr such that:

1) if the pencil (A,B) has two real eigenvalues (include 0/0 or 1/0 types), then

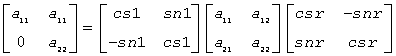
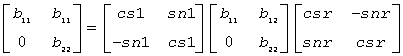
2) if the pencil (A,B) has a pair of complex conjugate eigenvalues, then

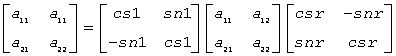
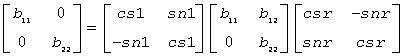
where b₁₁≥b₂₂>0.

Input Parameters

a, b

REAL for slagv2

DOUBLE PRECISION for dlagv2

Arrays:

a(lda,2) contains the 2-by-2 matrix A;

b(ldb,2) contains the upper triangular 2-by-2 matrix B.

lda

INTEGER. The leading dimension of the array a;

lda≥ 2.

ldb

INTEGER. The leading dimension of the array b;

ldb≥ 2.

Output Parameters

a

On exit, a is overwritten by the "A-part" of the generalized Schur form.

b

On exit, b is overwritten by the "B-part" of the generalized Schur form.

alphar, alphai, beta

REAL for slagv2

DOUBLE PRECISION for dlagv2.

Arrays, dimension (2) each.

(alphar(k) + i*alphai(k))/beta(k) are the eigenvalues of the pencil (A,B), k=1,2 and i = sqrt(-1).

Note that beta(k) may be zero.

csl, snl

REAL for slagv2

DOUBLE PRECISION for dlagv2

The cosine and sine of the left rotation matrix, respectively.

csr, snr

REAL for slagv2

DOUBLE PRECISION for dlagv2

The cosine and sine of the right rotation matrix, respectively.