Solves a real quasi-triangular system of equations, or a complex quasi-triangular system of special form, in real arithmetic.
Syntax
call slaqtr( ltran, lreal, n, t, ldt, b, w, scale, x, work, info )
call dlaqtr( ltran, lreal, n, t, ldt, b, w, scale, x, work, info )
Include Files
- mkl.fi
Description
The routine ?laqtr solves the real quasi-triangular system
op(T) * p = scale*c, if lreal = .TRUE.
or the complex quasi-triangular systems
op(T + iB)*(p+iq) = scale*(c+id), if lreal = .FALSE.
in real arithmetic, where T is upper quasi-triangular.
If lreal = .FALSE., then the first diagonal block of T must be 1-by-1, B is the specially structured matrix
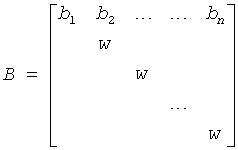
op(A) = A or AT, AT denotes the transpose of matrix A.
On input,
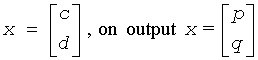
This routine is designed for the condition number estimation in routine ?trsna.
Input Parameters
- ltran
LOGICAL.
On entry, ltran specifies the option of conjugate transpose:
= .FALSE., op(T + iB) = T + iB,
= .TRUE., op(T + iB) = (T + iB)T.
- lreal
LOGICAL.
On entry, lreal specifies the input matrix structure:
= .FALSE., the input is complex
= .TRUE., the input is real.
- n
INTEGER.
On entry, n specifies the order of T + iB. n≥ 0.
- t
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
Array, dimension (ldt,n). On entry, t contains a matrix in Schur canonical form. If lreal = .FALSE., then the first diagonal block of t must be 1-by-1.
- ldt
INTEGER. The leading dimension of the matrix T.
ldt≥ max(1,n).
- b
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
Array, dimension (n). On entry, b contains the elements to form the matrix B as described above. If lreal = .TRUE., b is not referenced.
- w
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
On entry, w is the diagonal element of the matrix B.
If lreal = .TRUE., w is not referenced.
- x
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
Array, dimension (2n). On entry, x contains the right hand side of the system.
- work
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
Workspace array, dimension (n).
Output Parameters
- scale
REAL for slaqtr
DOUBLE PRECISION for dlaqtr
On exit, scale is the scale factor.
- x
On exit, X is overwritten by the solution.
- info
INTEGER.
If info = 0: successful exit.
If info = 1: the some diagonal 1-by-1 block has been perturbed by a small number smin to keep nonsingularity.
If info = 2: the some diagonal 2-by-2 block has been perturbed by a small number in ?laln2 to keep nonsingularity.
Note
For higher speed, this routine does not check the inputs for errors.