Applies a sequence of plane rotations to a general rectangular matrix.
Syntax
call slasr( side, pivot, direct, m, n, c, s, a, lda )
call dlasr( side, pivot, direct, m, n, c, s, a, lda )
call clasr( side, pivot, direct, m, n, c, s, a, lda )
call zlasr( side, pivot, direct, m, n, c, s, a, lda )
Include Files
- mkl.fi
Description
The routine applies a sequence of plane rotations to a real/complex matrix A, from the left or the right.
A := P*A, when side = 'L' ( Left-hand side )
A := A*P', when side = 'R' ( Right-hand side )
where P is an orthogonal matrix consisting of a sequence of plane rotations with z = m when side = 'L' and z = n when side = 'R'.
When direct = 'F' (Forward sequence), then
P = P(z-1)*...P(2)*P(1),
and when direct = 'B' (Backward sequence), then
P = P(1)*P(2)*...*P(z-1),
where P( k ) is a plane rotation matrix defined by the 2-by-2 plane rotation:
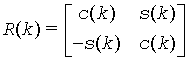
When pivot = 'V' ( Variable pivot ), the rotation is performed for the plane (k, k + 1), that is, P(k) has the form
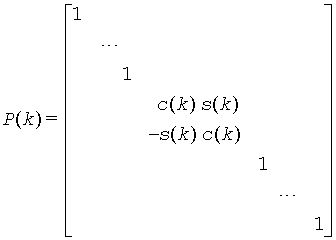
where R(k) appears as a rank-2 modification to the identity matrix in rows and columns k and k+1.
When pivot = 'T' ( Top pivot ), the rotation is performed for the plane (1,k+1), so P(k) has the form
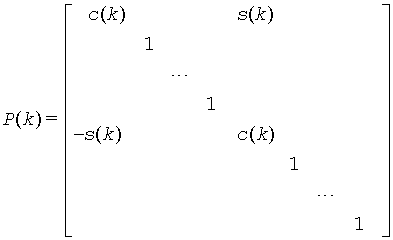
where R(k) appears in rows and columns k and k+1.
Similarly, when pivot = 'B' ( Bottom pivot ), the rotation is performed for the plane (k,z), giving P(k) the form
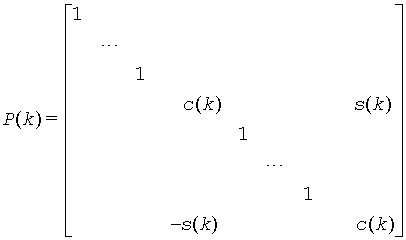
where R(k) appears in rows and columns k and z. The rotations are performed without ever forming P(k) explicitly.
Input Parameters
- side
CHARACTER*1. Specifies whether the plane rotation matrix P is applied to A on the left or the right.
= 'L': left, compute A := P*A
= 'R': right, compute A:= A*P'
- direct
CHARACTER*1. Specifies whether P is a forward or backward sequence of plane rotations.
= 'F': forward, P = P(z-1)*...*P(2)*P(1)
= 'B': backward, P = P(1)*P(2)*...*P(z-1)
- pivot
CHARACTER*1. Specifies the plane for which P(k) is a plane rotation matrix.
= 'V': Variable pivot, the plane (k, k+1)
= 'T': Top pivot, the plane (1, k+1)
= 'B': Bottom pivot, the plane (k, z)
- m
INTEGER. The number of rows of the matrix A.
If m ≤ 1, an immediate return is effected.
- n
INTEGER. The number of columns of the matrix A.
If n ≤ 1, an immediate return is effected.
- c, s
REAL for slasr/clasr
DOUBLE PRECISION for dlasr/zlasr.
Arrays, DIMENSION
(m-1) if side = 'L',
(n-1) if side = 'R' .
c(k) and s(k) contain the cosine and sine of the plane rotations respectively that define the 2-by-2 plane rotation part (R(k)) of the P(k) matrix as described above in Description.
- a
REAL for slasr
DOUBLE PRECISION for dlasr
COMPLEX for clasr
DOUBLE COMPLEX for zlasr.
Array, DIMENSION (lda, n).
The m-by-n matrix A.
- lda
INTEGER. The leading dimension of the array a.
lda≥ max(1,m).
Output Parameters
- a
On exit, A is overwritten by P*A if side = 'R', or by A*P' if side = 'L'.