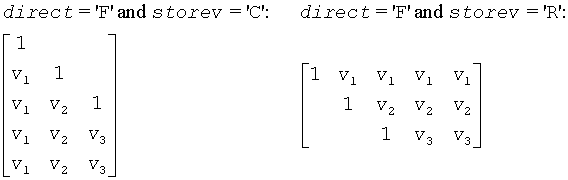?larfb

Syntax

call slarfb( side, trans, direct, storev, m, n, k, v, ldv, t, ldt, c, ldc, work, ldwork )

call dlarfb( side, trans, direct, storev, m, n, k, v, ldv, t, ldt, c, ldc, work, ldwork )

call clarfb( side, trans, direct, storev, m, n, k, v, ldv, t, ldt, c, ldc, work, ldwork )

call zlarfb( side, trans, direct, storev, m, n, k, v, ldv, t, ldt, c, ldc, work, ldwork )

Include Files

• mkl.fi

Description

The real flavors of the routine ?larfb apply a real block reflector H or its transpose H^T to a real m-by-n matrix C from either left or right.

The complex flavors of the routine ?larfb apply a complex block reflector H or its conjugate transpose H^H to a complex m-by-n matrix C from either left or right.

Input Parameters

The data types are given for the Fortran interface.

side

CHARACTER*1.

If side = 'L': apply H or H^T for real flavors and H or H^H for complex flavors from the left.

If side = 'R': apply H or H^T for real flavors and H or H^H for complex flavors from the right.

trans

CHARACTER*1.

If trans = 'N': apply H (No transpose).

If trans = 'C': apply H^H (Conjugate transpose).

If trans = 'T': apply H^T (Transpose).

direct

CHARACTER*1.

Indicates how H is formed from a product of elementary reflectors

If direct = 'F': H = H(1)*H(2)*. . . *H(k) (forward)

If direct = 'B': H = H(k)* . . . H(2)*H(1) (backward)

storev

CHARACTER*1.

Indicates how the vectors which define the elementary reflectors are stored:

If storev = 'C': Column-wise

If storev = 'R': Row-wise

m

INTEGER. The number of rows of the matrix C.

n

INTEGER. The number of columns of the matrix C.

k

INTEGER. The order of the matrix T (equal to the number of elementary reflectors whose product defines the block reflector).

v

REAL for slarfb

DOUBLE PRECISION for dlarfb

COMPLEX for clarfb

DOUBLE COMPLEX for zlarfb

Array, DIMENSION

(ldv, k) if storev = 'C'

(ldv, m) if storev = 'R' and side = 'L'

(ldv, n) if storev = 'R' and side = 'R'

The matrix v. See Application Notes below.

ldv

INTEGER. The leading dimension of the array v.

If storev = 'C' and side = 'L', ldv≥ max(1,m);

if storev = 'C' and side = 'R', ldv≥ max(1,n);

if storev = 'R', ldv≥k.

t

REAL for slarfb

DOUBLE PRECISION for dlarfb

COMPLEX for clarfb

DOUBLE COMPLEX for zlarfb

Array, size (ldt,k).

Contains the triangular k-by-k matrix T in the representation of the block reflector.

ldt

INTEGER. The leading dimension of the array t.

ldt≥k.

c

REAL for slarfb

DOUBLE PRECISION for dlarfb

COMPLEX for clarfb

DOUBLE COMPLEX for zlarfb

Array, size (ldc,n).

On entry, the m-by-n matrix C.

ldc

INTEGER. The leading dimension of the array c.

ldc≥ max(1,m).

work

REAL for slarfb

DOUBLE PRECISION for dlarfb

COMPLEX for clarfb

DOUBLE COMPLEX for zlarfb

Workspace array, DIMENSION (ldwork, k).

ldwork

INTEGER. The leading dimension of the array work.

If side = 'L', ldwork≥ max(1, n);

if side = 'R', ldwork≥ max(1, m).

Output Parameters

c

On exit, c is overwritten by the product of the following:

• H*C, or H^T*C, or C*H, or C*H^T for real flavors

• H*C, or H^H*C, or C*H, or C*H^H for complex flavors

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = -1011, memory allocation error occurred.

Application Notes

The shape of the matrix V and the storage of the vectors which define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.