?potrf2

Syntax

call spotrf2(uplo, n, a, lda, info)

call dpotrf2(uplo, n, a, lda, info)

call cpotrf2(uplo, n, a, lda, info)

call zpotrf2(uplo, n, a, lda, info)

Include Files

• mkl.fi

Description

?potrf2 computes the Cholesky factorization of a real or complex symmetric positive definite matrix A using the recursive algorithm.

The factorization has the form

for real flavors:

A = U^T * U, if uplo = 'U', or

A = L * L^T, if uplo = 'L',

for complex flavors:

A = U^H * U, if uplo = 'U',

or A = L * L^H, if uplo = 'L',

where U is an upper triangular matrix and L is lower triangular.

This is the recursive version of the algorithm. It divides the matrix into four submatrices:

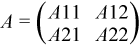
where A11 is n1 by n1 and A22 is n2 by n2, with n1 = n/2 and n2 = n-n1.

The subroutine calls itself to factor A11. Update and scale A21 or A12, update A22 then call itself to factor A22.

Input Parameters

uplo

CHARACTER*1. = 'U': Upper triangle of A is stored;

= 'L': Lower triangle of A is stored.

n

INTEGER. The order of the matrix A.

n≥ 0.

a

REAL for spotrf2

DOUBLE PRECISION for dpotrf2

COMPLEX for cpotrf2

DOUBLE COMPLEX for zpotrf2

Array, size (lda, n).

On entry, the symmetric matrix A.

If uplo = 'U', the leading n-by-n upper triangular part of a contains the upper triangular part of the matrix A, and the strictly lower triangular part of a is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of a contains the lower triangular part of the matrix A, and the strictly upper triangular part of a is not referenced.

lda

INTEGER. The leading dimension of the array a.

lda≥ max(1,n).

Output Parameters