Solves a system of linear equations with a tridiagonal coefficient matrix using the LU factorization computed by ?gttrf.
Syntax
lapack_int LAPACKE_sgttrs (int matrix_layout , char trans , lapack_int n , lapack_int nrhs , const float * dl , const float * d , const float * du , const float * du2 , const lapack_int * ipiv , float * b , lapack_int ldb );
lapack_int LAPACKE_dgttrs (int matrix_layout , char trans , lapack_int n , lapack_int nrhs , const double * dl , const double * d , const double * du , const double * du2 , const lapack_int * ipiv , double * b , lapack_int ldb );
lapack_int LAPACKE_cgttrs (int matrix_layout , char trans , lapack_int n , lapack_int nrhs , const lapack_complex_float * dl , const lapack_complex_float * d , const lapack_complex_float * du , const lapack_complex_float * du2 , const lapack_int * ipiv , lapack_complex_float * b , lapack_int ldb );
lapack_int LAPACKE_zgttrs (int matrix_layout , char trans , lapack_int n , lapack_int nrhs , const lapack_complex_double * dl , const lapack_complex_double * d , const lapack_complex_double * du , const lapack_complex_double * du2 , const lapack_int * ipiv , lapack_complex_double * b , lapack_int ldb );
Include Files
- mkl.h
Description
The routine solves for X the following systems of linear equations with multiple right hand sides:
A*X = B |
if trans='N', |
AT*X = B |
if trans='T', |
AH*X = B |
if trans='C' (for complex matrices only). |
Before calling this routine, you must call ?gttrf to compute the LU factorization of A.
Input Parameters
matrix_layout |
Specifies whether matrix storage layout for array b is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR). |
trans |
Must be 'N' or 'T' or 'C'. Indicates the form of the equations: If trans = 'N', then A*X = B is solved for X. If trans = 'T', then AT*X = B is solved for X. If trans = 'C', then AH*X = B is solved for X. |
n |
The order of A; n≥ 0. |
nrhs |
The number of right-hand sides, that is, the number of columns in B; nrhs≥ 0. |
dl,d,du,du2 |
Arrays: dl(n -1), d(n), du(n -1), du2(n -2). The array dl contains the (n - 1) multipliers that define the matrix L from the LU factorization of A. The array d contains the n diagonal elements of the upper triangular matrix U from the LU factorization of A. The array du contains the (n - 1) elements of the first superdiagonal of U. The array du2 contains the (n - 2) elements of the second superdiagonal of U. |
b |
Array of size max(1, ldb*nrhs) for column major layout and max(1, n*ldb) for row major layout. Contains the matrix B whose columns are the right-hand sides for the systems of equations. |
ldb |
The leading dimension of b; ldb≥ max(1, n) for column major layout and ldb≥nrhs for row major layout. |
ipiv |
Array, size (n). The ipiv array, as returned by ?gttrf. |
Output Parameters
b |
Overwritten by the solution matrix X. |
Return Values
This function returns a value info.
If info=0, the execution is successful.
If info = -i, parameter i had an illegal value.
Application Notes
For each right-hand side b, the computed solution is the exact solution of a perturbed system of equations (A + E)x = b, where
|E| ≤ c(n)ε P|L||U|
c(n) is a modest linear function of n, and ε is the machine precision.
If x0 is the true solution, the computed solution x satisfies this error bound:
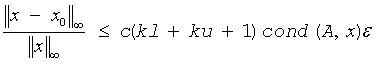
where cond(A,x)= || |A-1||A| |x| ||∞ / ||x||∞≤ ||A-1||∞ ||A||∞ = κ∞(A).
Note that cond(A,x) can be much smaller than κ∞(A); the condition number of AT and AH might or might not be equal to κ∞(A).
The approximate number of floating-point operations for one right-hand side vector b is 7n (including n divisions) for real flavors and 34n (including 2n divisions) for complex flavors.
To estimate the condition number κ∞(A), call ?gtcon.
To refine the solution and estimate the error, call ?gtrfs.