This topic describes LAPACK routines for solving nonsymmetric eigenvalue problems, computing the Schur factorization of general matrices, as well as performing a number of related computational tasks.
A nonsymmetric eigenvalue problem is as follows: given a nonsymmetric (or non-Hermitian) matrix A, find the eigenvaluesλ and the corresponding eigenvectorsz that satisfy the equation
Az = λz (right eigenvectors z)
or the equation
zHA = λzH (left eigenvectors z).
Nonsymmetric eigenvalue problems have the following properties:
The number of eigenvectors may be less than the matrix order (but is not less than the number of distinct eigenvalues of A).
Eigenvalues may be complex even for a real matrix A.
If a real nonsymmetric matrix has a complex eigenvalue a+bi corresponding to an eigenvector z, then a-bi is also an eigenvalue. The eigenvalue a-bi corresponds to the eigenvector whose elements are complex conjugate to the elements of z.
To solve a nonsymmetric eigenvalue problem with LAPACK, you usually need to reduce the matrix to the upper Hessenberg form and then solve the eigenvalue problem with the Hessenberg matrix obtained. Table "Computational Routines for Solving Nonsymmetric Eigenvalue Problems" lists LAPACK routines to reduce the matrix to the upper Hessenberg form by an orthogonal (or unitary) similarity transformation A = QHQH as well as routines to solve eigenvalue problems with Hessenberg matrices, forming the Schur factorization of such matrices and computing the corresponding condition numbers.
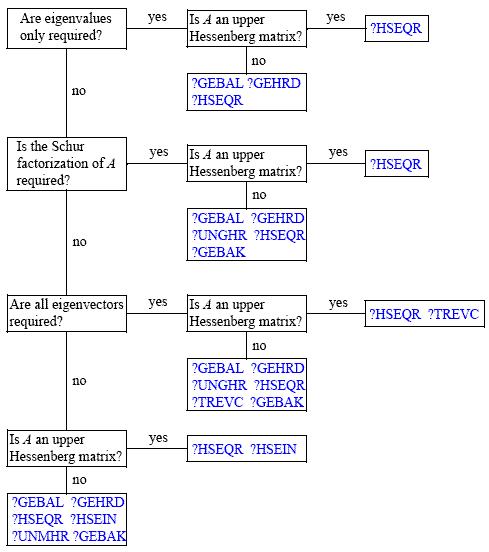
The decision tree in Figure "Decision Tree: Real Nonsymmetric Eigenvalue Problems" helps you choose the right routine or sequence of routines for an eigenvalue problem with a real nonsymmetric matrix. If you need to solve an eigenvalue problem with a complex non-Hermitian matrix, use the decision tree shown in Figure "Decision Tree: Complex Non-Hermitian Eigenvalue Problems".
Operation performed |
Routines for real matrices |
Routines for complex matrices |
|---|---|---|
Reduce to Hessenberg form A = QHQH |
||
Generate the matrix Q |
||
Apply the matrix Q |
||
Balance matrix |
||
Transform eigenvectors of balanced matrix to those of the original matrix |
||
Find eigenvalues and Schur factorization (QR algorithm) |
||
Find eigenvectors from Hessenberg form (inverse iteration) |
||
Find eigenvectors from Schur factorization |
||
Estimate sensitivities of eigenvalues and eigenvectors |
||
Reorder Schur factorization |
||
Reorder Schur factorization, find the invariant subspace and estimate sensitivities |
||
Solves Sylvester's equation. |
Decision Tree: Real Nonsymmetric Eigenvalue Problems
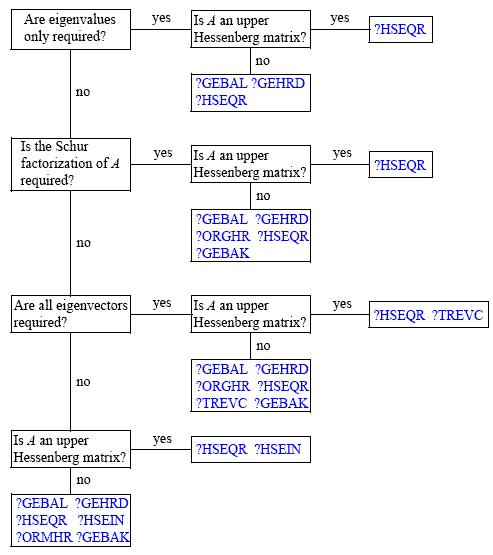
Decision Tree: Complex Non-Hermitian Eigenvalue Problems