Solves a nonlinear least squares problem using the TR algorithm.
Syntax
MKL_INT strnlsp_solve (_TRNSP_HANDLE_t* handle, float* fvec, float* fjac, MKL_INT* RCI_Request);
MKL_INT dtrnlsp_solve (_TRNSP_HANDLE_t* handle, double* fvec, double* fjac, MKL_INT* RCI_Request);
Include Files
- mkl.h
Description
The ?trnlsp_solve routine uses the TR algorithm to solve nonlinear least squares problems.
The problem is stated as follows:
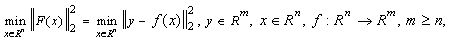
where
F(x):Rn → Rm
m ≥ n
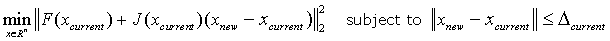
to get xnew = xcurrent + s that satisfies
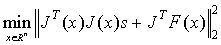
where
J(x) is the Jacobian matrix
s is the trial step
||s||2 ≤ Δcurrent
Δ is the trust-region area.
The RCI_Request parameter provides additional information:
RCI_Request Value |
Description |
|---|---|
2 |
Request to calculate the Jacobian matrix and put the result into fjac |
1 |
Request to recalculate the function at vector X and put the result into fvec |
0 |
One successful iteration step on the current trust-region radius (that does not mean that the value of x has changed) |
-1 |
The algorithm has exceeded the maximum number of iterations |
-2 |
Δ < eps[0] |
-3 |
||F(x)||2 < eps[1] |
-4 |
The Jacobian matrix is singular. ||J(x)[m*(j-1)...m*j-1]||2 < eps[2], j = 1, ..., n |
-5 |
||s||2 < eps[3] |
-6 |
||F(x)||2 - ||F(x) - J(x)s||2 < eps[4] |
Note
If it is possible to combine computations of the function and the jacobian (RCI_Request = 1 and 2), you can do that and provide both updated values for fvec and fjac as fulfillment of RCI_Request =1 (and do nothing for RCI_Request = 2).
Input Parameters
- handle
Type _TRNSP_HANDLE_t.
- fvec
Array of size m. Contains the function values at X, where fvec[i] = (yi – fi(x)).
- fjac
Array of size m by n. Contains the Jacobian matrix of the function.
Output Parameters
- fvec
Array of size m. Updated function evaluated at x.
- RCI_Request
Informs about the task stage.
See the Description section for the parameter values and their meaning.
- res
Indicates the task completion.
res = TR_SUCCESS - the routine completed the task normally.
TR_SUCCESS is defined in the mkl_rci.h include file.