?ppequ

Computes row and column scaling factors intended to equilibrate a symmetric (Hermitian) positive definite matrix in packed storage and reduce its condition number.

Syntax

FORTRAN 77:

call sppequ( uplo, n, ap, s, scond, amax, info )

call dppequ( uplo, n, ap, s, scond, amax, info )

call cppequ( uplo, n, ap, s, scond, amax, info )

call zppequ( uplo, n, ap, s, scond, amax, info )

FORTRAN 95:

call ppequ( ap, s [,scond] [,amax] [,uplo] [,info] )

lapack_int LAPACKE_sppequ( int matrix_order, char uplo, lapack_int n, const float* ap, float* s, float* scond, float* amax );

lapack_int LAPACKE_dppequ( int matrix_order, char uplo, lapack_int n, const double* ap, double* s, double* scond, double* amax );

lapack_int LAPACKE_cppequ( int matrix_order, char uplo, lapack_int n, const lapack_complex_float* ap, float* s, float* scond, float* amax );

lapack_int LAPACKE_zppequ( int matrix_order, char uplo, lapack_int n, const lapack_complex_double* ap, double* s, double* scond, double* amax );

Include Files

Fortran: mkl_lapack.fi and mkl_lapack.h
Fortran 95: lapack.f90
C: mkl_lapacke.h

Description

The routine computes row and column scalings intended to equilibrate a symmetric (Hermitian) positive definite matrix A in packed storage and reduce its condition number (with respect to the two-norm). The output array s returns scale factors computed as

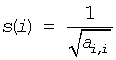
These factors are chosen so that the scaled matrix B with elements b_ij=s(i)*a_ij*s(j) has diagonal elements equal to 1.

This choice of s puts the condition number of B within a factor n of the smallest possible condition number over all possible diagonal scalings.

See ?laqsp auxiliary function that uses scaling factors computed by ?ppequ.

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

uplo

CHARACTER*1. Must be 'U' or 'L'.

Indicates whether the upper or lower triangular part of A is packed in the array ap:

If uplo = 'U', the array ap stores the upper triangular part of the matrix A.

If uplo = 'L', the array ap stores the lower triangular part of the matrix A.

INTEGER. The order of matrix A; n ≥ 0.

REAL for sppequ

DOUBLE PRECISION for dppequ

COMPLEX for cppequ

DOUBLE COMPLEX for zppequ.

Array, DIMENSION at least max(1,n(n+1)/2). The array ap contains the upper or the lower triangular part of the matrix A (as specified by uplo) in packed storage (see Matrix Storage Schemes).

Output Parameters

s	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. Array, DIMENSION (`n`). If `info = 0`, the array `s` contains the scale factors for `A`.
scond	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. If `info = 0`, `scond` contains the ratio of the smallest `s(i)` to the largest `s(i)`.
amax	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. Absolute value of the largest element of the matrix `A`.
info	INTEGER. If `info = 0`, the execution is successful. If `info = -i`, the `i`-th parameter had an illegal value. If `info = i`, the `i`-th diagonal element of `A` is nonpositive.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.

Specific details for the routine ppequ interface are as follows:

ap	Holds the array `A` of size (`n*(n+1)/2`).
s	Holds the vector of length `n`.
uplo	Must be 'U' or 'L'. The default value is 'U'.

Application Notes

If scond ≥ 0.1 and amax is neither too large nor too small, it is not worth scaling by s.

If amax is very close to overflow or very close to underflow, the matrix A should be scaled.