vRngHypergeometric

Generates hypergeometrically distributed random values.

Syntax

FORTRAN:

status = virnghypergeometric( method, stream, n, r, l, s, m )

status = viRngHypergeometric( method, stream, n, r, l, s, m );

Include Files

FORTRAN 77: mkl_vsl.f77
Fortran 90: mkl_vsl.f90
C: mkl_vsl_functions.h

Input Parameters

Name	Type	Description
method	FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int	Generation method. The specific value is as follows: `VSL_RNG_METHOD_HYPERGEOMETRIC_H2PE` See brief description of the H2PE method in Table "Values of `<method>` in method parameter"
stream	FORTRAN 77: INTEGER4 stream(2) Fortran 90:* TYPE (VSL_STREAM_STATE), INTENT(IN) C: VSLStreamStatePtr	Fortran: Descriptor of the stream state structure. C: Pointer to the stream state structure
n	FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int	Number of random values to be generated
l	FORTRAN 77: INTEGER4 Fortran 90:* INTEGER(KIND=4), INTENT(IN) C: const int	Lot size l
s	FORTRAN 77: INTEGER4 Fortran 90:* INTEGER(KIND=4), INTENT(IN) C: const int	Size of sampling without replacement s
m	FORTRAN 77: INTEGER4 Fortran 90:* INTEGER(KIND=4), INTENT(IN) C: const int	Number of marked elements m

Output Parameters

Name	Type	Description
r	FORTRAN 77: INTEGER4 Fortran 90:* INTEGER(KIND=4), INTENT(OUT) C: int*	Vector of `n` hypergeometrically distributed random values

Name

Type

Description

FORTRAN 77: INTEGER*4

Fortran 90: INTEGER(KIND=4), INTENT(OUT)

C: int*

Vector of n hypergeometrically distributed random values

Description

The vRngHypergeometric function generates hypergeometrically distributed random values with lot size l, size of sampling s, and number of marked elements in the lot m, where l, m, s∈N∪{0}; l ≥ max(s, m).

Consider a lot of l elements comprising m "marked" and l-m "unmarked" elements. A trial sampling without replacement of exactly s elements from this lot helps to define the hypergeometric distribution, which is the probability that the group of s elements contains exactly k marked elements.

The probability distribution is given by:)

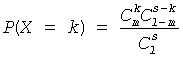
, k∈ {max(0, s + m - l), ..., min(s, m)}

The cumulative distribution function is as follows:

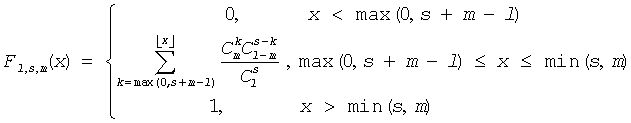
Return Values

VSL_ERROR_OK, VSL_STATUS_OK: Indicates no error, execution is successful.
VSL_ERROR_NULL_PTR: stream is a NULL pointer.
VSL_RNG_ERROR_BAD_STREAM: stream is not a valid random stream.
VSL_RNG_ERROR_BAD_UPDATE: Callback function for an abstract BRNG returns an invalid number of updated entries in a buffer, that is, < 0 or > nmax.
VSL_RNG_ERROR_NO_NUMBERS: Callback function for an abstract BRNG returns 0 as the number of updated entries in a buffer.
VSL_RNG_ERROR_QRNG_PERIOD_ELAPSED: Period of the generator has been exceeded.