Forms the triangular vector T of a block reflector H=I-V*T*VH.
Syntax
call pslarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)
call pdlarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)
call pclarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)
call pzlarft(direct, storev, n, k, v, iv, jv, descv, tau, t, work)
Description
The p?larft routine forms the triangular factor T of a real/complex block reflector H of order n, which is defined as a product of k elementary reflectors.
If direct = 'F', H = H(1)*H(2)...*H(k), and T is upper triangular;
If direct = 'B', H = H(k)*...*H(2)*H(1), and T is lower triangular.
If storev = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the distributed matrix V, and
H = I-V*T*V'
If storev = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the distributed matrix V, and
H = I-V'*T*V.
Input Parameters
- direct
(global) CHARACTER*1.
Specifies the order in which the elementary reflectors are multiplied to form the block reflector:
if direct = 'F': H = H(1)*H(2)*...*H(k) (forward)
if direct = 'B': H = H(k)*...*H(2)*H(1) (backward).
- storev
(global) CHARACTER*1.
Specifies how the vectors that define the elementary reflectors are stored (See Application Notes below):
if storev = 'C': columnwise;
if storev = 'R': rowwise.
- n
(global) INTEGER.
The order of the block reflector H. n ≥ 0.
- k
(global) INTEGER.
The order of the triangular factor T, is equal to the number of elementary reflectors.
1 ≤ k ≤ mb_v (= nb_v).
- v
REAL for pslarft
DOUBLE PRECISION for pdlarft
COMPLEX for pclarft
COMPLEX*16 for pzlarft.
Pointer into the local memory to an array of local DIMENSION
(LOCr(iv+n-1), LOCc(jv+k-1)) if storev = 'C', and
(LOCr(iv+k-1), LOCc(jv+n-1)) if storev = 'R'.
The distributed matrix V contains the Householder vectors. (See Application Notes below).
- iv, jv
(global) INTEGER.
The row and column indices in the global array v indicating the first row and the first column of the submatrix sub(V), respectively.
- descv
(global and local) INTEGER array, DIMENSION (dlen_). The array descriptor for the distributed matrix V.
- tau
(local)
REAL for pslarft
DOUBLE PRECISION for pdlarft
COMPLEX for pclarft
COMPLEX*16 for pzlarft.
Array, DIMENSIONLOCr(iv+k-1) if incv = m_v, and LOCc(jv+k-1) otherwise. This array contains the Householder scalars related to the Householder vectors.
tau is tied to the distributed matrix V.
- work
(local).
REAL for pslarft
DOUBLE PRECISION for pdlarft
COMPLEX for pclarft
COMPLEX*16 for pzlarft.
Workspace array, DIMENSION (k*(k-1)/2).
Output Parameters
- v
REAL for pslarft
DOUBLE PRECISION for pdlarft
COMPLEX for pclarft
COMPLEX*16 for pzlarft.
- t
(local)
REAL for pslarft
DOUBLE PRECISION for pdlarft
COMPLEX for pclarft
COMPLEX*16 for pzlarft.
Array, DIMENSION (nb_v,nb_v) if storev = 'C', and (mb_v,mb_v) otherwise. It contains the k-by-k triangular factor of the block reflector associated with v. If direct = 'F', t is upper triangular;
if direct = 'B', t is lower triangular.
Application Notes
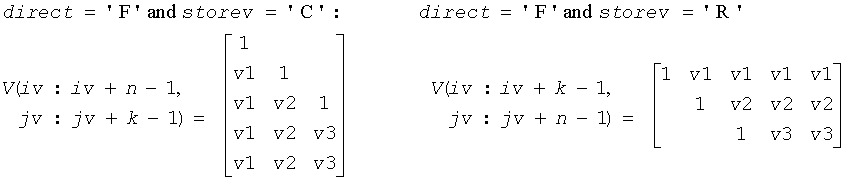
The shape of the matrix V and the storage of the vectors that define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.