Nonlinear Least Squares Problem without Constraints

The nonlinear least squares problem without constraints can be described as follows:

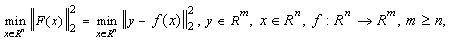
where

F(x) : Rⁿ → R^m is a twice differentiable function in Rⁿ.

Solving a nonlinear least squares problem means searching for the best approximation to the vector y with the model function f_i(x) and nonlinear variables x. The best approximation means that the sum of squares of residuals y_i - f_i(x) is the minimum.

See usage examples in FORTRAN and C in the examples\solver\source folder of your Intel MKL directory (ex_nlsqp_f.f and ex_nlsqp_c.c, respectively).

RCI TR Routines
Routine Name	Operation
?trnlsp_init	Initializes the solver.
?trnlsp_check	Checks correctness of the input parameters.
?trnlsp_solve	Solves a nonlinear least squares problem using the Trust-Region algorithm.
?trnlsp_get	Retrieves the number of iterations, stop criterion, initial residual, and final residual.
?trnlsp_delete	Releases allocated data.