Solves a system of linear equations with a triangular matrix, with multiple right-hand sides.
Syntax
FORTRAN 77:
call strtrs( uplo, trans, diag, n, nrhs, a, lda, b, ldb, info )
call dtrtrs( uplo, trans, diag, n, nrhs, a, lda, b, ldb, info )
call ctrtrs( uplo, trans, diag, n, nrhs, a, lda, b, ldb, info )
call ztrtrs( uplo, trans, diag, n, nrhs, a, lda, b, ldb, info )
FORTRAN 95:
call trtrs( a, b [,uplo] [, trans] [,diag] [,info] )
C:
lapack_int LAPACKE_<?>trtrs( int matrix_order, char uplo, char trans, char diag, lapack_int n, lapack_int nrhs, const <datatype>* a, lapack_int lda, <datatype>* b, lapack_int ldb );
Description
The routine solves for X the following systems of linear equations with a triangular matrix A, with multiple right-hand sides stored in B:
A*X = B |
if trans='N', |
AT*X = B |
if trans='T', |
AH*X = B |
if trans='C' (for complex matrices only). |
Input Parameters
The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.
uplo |
CHARACTER*1. Must be 'U' or 'L'. Indicates whether A is upper or lower triangular: If uplo = 'U', then A is upper triangular. If uplo = 'L', then A is lower triangular. |
trans |
CHARACTER*1. Must be 'N' or 'T' or 'C'. If trans = 'N', then A*X = B is solved for X. If trans = 'T', then AT*X = B is solved for X. If trans = 'C', then AH*X = B is solved for X. |
diag |
CHARACTER*1. Must be 'N' or 'U'. If diag = 'N', then A is not a unit triangular matrix. If diag = 'U', then A is unit triangular: diagonal elements of A are assumed to be 1 and not referenced in the array a. |
n |
INTEGER. The order of A; the number of rows in B; n ≥ 0. |
nrhs |
INTEGER. The number of right-hand sides; nrhs ≥ 0. |
a, b |
REAL for strtrs DOUBLE PRECISION for dtrtrs COMPLEX for ctrtrs DOUBLE COMPLEX for ztrtrs. Arrays: a(lda,*), b(ldb,*). The array a contains the matrix A. The array b contains the matrix B whose columns are the right-hand sides for the systems of equations. The second dimension of a must be at least max(1,n), the second dimension of b at least max(1,nrhs). |
lda |
INTEGER. The leading dimension of a; lda ≥ max(1, n). |
ldb |
INTEGER. The leading dimension of b; ldb ≥ max(1, n). |
Output Parameters
b |
Overwritten by the solution matrix X. |
info |
INTEGER. If info=0, the execution is successful. If info = -i, the i-th parameter had an illegal value. |
Fortran 95 Interface Notes
Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.
Specific details for the routine trtrs interface are as follows:
a |
Stands for argument ap in FORTRAN 77 interface. Holds the matrix A of size (n*(n+1)/2). |
b |
Holds the matrix B of size (n, nrhs). |
uplo |
Must be 'U' or 'L'. The default value is 'U'. |
trans |
Must be 'N', 'C', or 'T'. The default value is 'N'. |
diag |
Must be 'N' or 'U'. The default value is 'N'. |
Application Notes
For each right-hand side b, the computed solution is the exact solution of a perturbed system of equations (A + E)x = b, where
|E| ≤ c(n)ε |A|
c(n) is a modest linear function of n, and ε is the machine precision. If x0 is the true solution, the computed solution x satisfies this error bound:
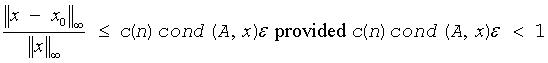
where cond(A,x)= || |A-1||A| |x| ||∞ / ||x||∞ ≤ ||A-1||∞ ||A||∞ = κ∞(A).
Note that cond(A,x) can be much smaller than κ∞(A); the condition number of AT and AH might or might not be equal to κ∞(A).
The approximate number of floating-point operations for one right-hand side vector b is n2 for real flavors and 4n2 for complex flavors.
To estimate the condition number κ∞(A), call ?trcon.
To estimate the error in the solution, call ?trrfs.