?pbequ

Computes row and column scaling factors intended to equilibrate a symmetric (Hermitian) positive-definite band matrix and reduce its condition number.

Syntax

FORTRAN 77:

call spbequ( uplo, n, kd, ab, ldab, s, scond, amax, info )

call dpbequ( uplo, n, kd, ab, ldab, s, scond, amax, info )

call cpbequ( uplo, n, kd, ab, ldab, s, scond, amax, info )

call zpbequ( uplo, n, kd, ab, ldab, s, scond, amax, info )

FORTRAN 95:

call pbequ( ab, s [,scond] [,amax] [,uplo] [,info] )

lapack_int LAPACKE_spbequ( int matrix_order, char uplo, lapack_int n, lapack_int kd, const float* ab, lapack_int ldab, float* s, float* scond, float* amax );

lapack_int LAPACKE_dpbequ( int matrix_order, char uplo, lapack_int n, lapack_int kd, const double* ab, lapack_int ldab, double* s, double* scond, double* amax );

lapack_int LAPACKE_cpbequ( int matrix_order, char uplo, lapack_int n, lapack_int kd, const lapack_complex_float* ab, lapack_int ldab, float* s, float* scond, float* amax );

lapack_int LAPACKE_zpbequ( int matrix_order, char uplo, lapack_int n, lapack_int kd, const lapack_complex_double* ab, lapack_int ldab, double* s, double* scond, double* amax );

Include Files

Fortran: mkl_lapack.fi and mkl_lapack.h
Fortran 95: lapack.f90
C: mkl_lapacke.h

Description

The routine computes row and column scalings intended to equilibrate a symmetric (Hermitian) positive definite matrix A in packed storage and reduce its condition number (with respect to the two-norm). The output array s returns scale factors computed as

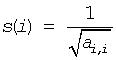
These factors are chosen so that the scaled matrix B with elements b_ij=s(i)*a_ij*s(j) has diagonal elements equal to 1. This choice of s puts the condition number of B within a factor n of the smallest possible condition number over all possible diagonal scalings.

See ?laqsb auxiliary function that uses scaling factors computed by ?pbequ.

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

uplo	CHARACTER*1. Must be 'U' or 'L'. Indicates whether the upper or lower triangular part of `A` is packed in the array `ab`: If `uplo = 'U'`, the array `ab` stores the upper triangular part of the matrix `A`. If `uplo = 'L'`, the array `ab` stores the lower triangular part of the matrix `A`.
n	INTEGER. The order of matrix `A`; `n ≥ 0`.
kd	INTEGER. The number of superdiagonals or subdiagonals in the matrix `A`; `kd` ≥ 0.
ab	REAL for spbequ DOUBLE PRECISION for dpbequ COMPLEX for cpbequ DOUBLE COMPLEX for zpbequ. Array, DIMENSION `(ldab,*)`. The array `ap` contains either the upper or the lower triangular part of the matrix `A` (as specified by `uplo`) in band storage (see Matrix Storage Schemes). The second dimension of `ab` must be at least `max(1, n)`.
ldab	INTEGER. The leading dimension of the array `ab`; `ldab` ≥ `kd` +1.

Output Parameters

s	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. Array, DIMENSION (`n`). If `info = 0`, the array `s` contains the scale factors for `A`.
scond	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. If `info = 0`, `scond` contains the ratio of the smallest `s(i)` to the largest `s(i)`.
amax	REAL for single precision flavors DOUBLE PRECISION for double precision flavors. Absolute value of the largest element of the matrix `A`.
info	INTEGER. If `info = 0`, the execution is successful. If `info = -i`, the `i`-th parameter had an illegal value. If `info = i`, the `i`-th diagonal element of `A` is nonpositive.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.

Specific details for the routine pbequ interface are as follows:

ab	Holds the array `A` of size (`kd+1,n`).
s	Holds the vector of length `n`.
uplo	Must be 'U' or 'L'. The default value is 'U'.

Application Notes

If scond ≥ 0.1 and amax is neither too large nor too small, it is not worth scaling by s.

If amax is very close to overflow or very close to underflow, the matrix A should be scaled.