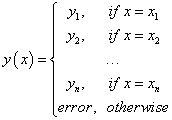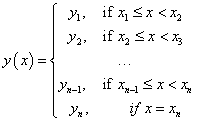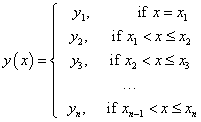Mathematical Conventions

This section explains the notation used for Data Fitting function descriptions. Spline notations are based on the terminology and definitions of [deBoor2001]. The definition of Subbotin quadratic splines follows the conventions of [StechSub76].

Mathematical Notation in the Data Fitting Component
Concept Mathematical Notation

Partition of interpolation interval [a, b] , where

  • xi denotes breakpoints.
  • [xi, xi+1) denotes a sub-interval (cell) of size Δxi+1-xi .

{xi}i=1,...,n, where a = x1 < x2<... <xn = b

Vector-valued function of dimension p being fit

ƒ(x) = (ƒ1(x),..., ƒp(x))

Piecewise polynomial (PP) function ƒ of order k+1

ƒ(x) ≔ Pi (x), if x ∈ [ xi, xi+1), i = 1,..., n-1

where

  • {xi}i= 1,..., n is a strictly increasing sequence of breakpoints.
  • Pi(x) = ci,0 + ci,1(x - xi) + ... + ci,k(x - xi)k is a polynomial of degree k (order k+1) over the interval x ∈ [ xi, xi+1).

Function p agrees with function g at the points {xi}i=1,...,n .

For every point ζ in sequence {xi}i=1,...,n that occurs m times, the equality p(i-1)(ζ) = g(i-1)(ζ) holds for all i = 1,...,m, where p(i)(t) is the derivative of the i-th order.

The k-th divided difference of function g at points xi,..., xi + k. This difference is the leading coefficient of the polynomial of order k+1 that agrees with g at xi,..., xi + k.

[ xi,..., xi + k] g

In particular,

  • [x1]g = g(x1)
  • [ x1, x2] g = (g(x1) - g(x2)) / (x1 - x2)

A k-order derivative of interpolant ƒ(x) at interpolation site .

Interpolants to the Function g at xi,..., xn and Boundary Conditions
Concept Mathematical Notation

Linear interpolant

Pi(x) = c1, i + c2, i(x - xi),

where

  • x ∈ [ xi, xi+1)
  • c1, i = g(xi)
  • c2, i = [xi, xi+1 ]g
  • i = 1,..., n-1

Piecewise parabolic interpolant

Pi(x) = c1, i + c2, i(x - xi) + c3, i(x - xi)2, x ∈ [ xi, xi+1)

Coefficients c1, i, c2, i, and c3, i depend on the conditions:

  • Pi(xi) = g(xi)
  • Pi(xi+1) = g(xi+1)
  • Pi((xi+1 + xi) / 2) = vi+1

where parameter vi+1 depends on the interpolant being continuously differentiable:

Pi-1(1)(xi) = Pi(1)(xi)

Piecewise parabolic Subbotin interpolant

P(x) = Pi(x) = c1,i+c2,i(x-xi)+c3,i(x-xi)2+d3,i((x-ti)+)2,

where

  • x ∈ [ ti, ti+1)

  • {ti}i=1,...,n+1 is a sequence of knots such that

    • t1 = x1, tn+1 = xn

    • ti ∈ (xi-1, xi), i = 2,..., n

Coefficients c1,i, c2,i, c3,i, and d3,i depend on the following conditions:

  • Pi(xi) = g(xi), Pi(xi+1) = g(xi+1)
  • P(x) is a continuously differentiable polynomial of the second degree on [ ti, ti+1), i = 1,..., n.

Piecewise cubic Hermite interpolant

Pi(x) = c1,i + c2,i(x - xi) + c3,i(x - xi)2 + c4,i(x - xi)3,

where

  • x ∈ [ xi, xi+1)
  • c1,i = g(xi)
  • c2,i = si
  • c3,i = ([xi, xi+1]g - si ) / (Δxi) - c4,i(Δxi)
  • c4,i = (si + si+1 - 2[xi, xi+1]g) / (Δxi)2
  • i = 1,..., n-1
  • si = g(1)(xi)

Piecewise cubic Bessel interpolant

Pi(x) = c1,i + c2,i(x - xi) + c3,i(x - xi)2 + c4,i(x - xi)3,

where

  • x ∈ [ xi, xi+1)
  • c1,i = g(xi)
  • c2,i = si
  • c3,i = ([xi, xi+1]g - si ) / (Δxi) - c4,i(Δxi)
  • c4,i = (si + si+1 - 2[xi, xi+1]g) / (Δxi)2
  • i = 1,..., n-1
  • si = (Δxi[xi-1, xi]g + Δxi-1[xi, xi+1]g) / (Δxi + Δxi+1)

Piecewise cubic Akima interpolant

Pi(x) = c1,i + c2,i(x - xi) + c3,i(x - xi)2 + c4,i(x - xi)3,

where

  • x ∈ [ xi, xi+1)
  • c1,i = g(xi)
  • c2,i = si
  • c3,i = ([xi, xi+1]g - si ) / (Δxi) - c4,i(Δxi)
  • c4,i = (si + si+1 - 2[xi, xi+1]g) / (Δxi)2
  • i = 1,..., n-1
  • si = (wi+1[xi-1, xi]g + wi-1[xi, xi+1]g) / (wi+1 + wi-1),

    where

    wi = |[xi, xi+1]g - [xi-1, xi]g|

Piecewise natural cubic interpolant

Pi(x) = c1,i + c2,i(x - xi) + c3,i(x - xi)2 + c4,i(x - xi)3,

where

  • x ∈ [ xi, xi+1)
  • c1,i = g(xi)
  • c2,i = si
  • c3,i = ([xi, xi+1]g - si ) / (Δxi) - c4,i(Δxi)
  • c4,i = (si + si+1 - 2[xi, xi+1]g) / (Δxi)2
  • i = 1,..., n-1
  • Parameter si depends on the condition that the interpolant is twice continuously differentiable: Pi-1(2)(xi) = Pi(2)(xi).

Not-a-knot boundary condition.

Parameters s1 and sn provide P1 = P2 and Pn-1 = Pn, so that the first and the last interior breakpoints are inactive.

Free-end boundary condition.

ƒ"(x1) = ƒ"(xn) = 0

Look-up interpolator for discrete set of points (x1, y1),..., (xn, yn) .

Step-wise constant continuous right interpolator.

Step-wise constant continuous left interpolator.

Parent topic: Data Fitting Functions

Submit feedback on this help topic