?potrf

Computes the Cholesky factorization of a symmetric (Hermitian) positive-definite matrix.

Syntax

FORTRAN 77:

call spotrf( uplo, n, a, lda, info )

call dpotrf( uplo, n, a, lda, info )

call cpotrf( uplo, n, a, lda, info )

call zpotrf( uplo, n, a, lda, info )

FORTRAN 95:

call potrf( a [, uplo] [,info] )

lapack_int LAPACKE_<?>potrf( int matrix_order, char uplo, lapack_int n, <datatype>* a, lapack_int lda );

Include Files

Fortran: mkl_lapack.fi and mkl_lapack.h
Fortran 95: lapack.f90
C: mkl_lapacke.h

Description

The routine forms the Cholesky factorization of a symmetric positive-definite or, for complex data, Hermitian positive-definite matrix A:

`A = U^TU` for real data, `A = U^HU` for complex data	if `uplo='U'`
`A = LL^T` for real data, `A = LL^H` for complex data	if `uplo='L'`

where L is a lower triangular matrix and U is upper triangular.

Note

This routine supports the Progress Routine feature. See Progress Function for details.

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

uplo	CHARACTER*1. Must be 'U' or 'L'. Indicates whether the upper or lower triangular part of `A` is stored and how `A` is factored: If `uplo` = 'U', the array `a` stores the upper triangular part of the matrix `A`. If `uplo` = 'L', the array `a` stores the lower triangular part of the matrix `A`.
n	INTEGER. The order of matrix `A`; `n` ≥ 0.
a	REAL for spotrf DOUBLE PRECISION for dpotrf COMPLEX for cpotrf DOUBLE COMPLEX for zpotrf. Array, DIMENSION `(lda,*)`. The array `a` contains either the upper or the lower triangular part of the matrix `A` (see `uplo`). The second dimension of `a` must be at least `max(1, n)`.
lda	INTEGER. The leading dimension of `a`.

Output Parameters

The upper or lower triangular part of a is overwritten by the Cholesky factor U or L, as specified by uplo.

info

INTEGER. If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, the leading minor of order i (and therefore the matrix A itself) is not positive-definite, and the factorization could not be completed. This may indicate an error in forming the matrix A.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.

Specific details for the routine potrf interface are as follows:

a	Holds the matrix `A` of size (`n`, `n`).
uplo	Must be 'U' or 'L'. The default value is 'U'.

Application Notes

If uplo = 'U', the computed factor U is the exact factor of a perturbed matrix A + E, where

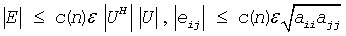
c(n) is a modest linear function of n, and ε is the machine precision.

A similar estimate holds for uplo = 'L'.

The total number of floating-point operations is approximately (1/3)n³ for real flavors or (4/3)n³ for complex flavors.

After calling this routine, you can call the following routines:

?potrs	to solve `A*X = B`
?pocon	to estimate the condition number of `A`
?potri	to compute the inverse of `A`.