Reduces an upper trapezoidal matrix to upper triangular form by means of orthogonal/unitary transformations.
Syntax
call pslatrz(m, n, l, a, ia, ja, desca, tau, work)
call pdlatrz(m, n, l, a, ia, ja, desca, tau, work)
call pclatrz(m, n, l, a, ia, ja, desca, tau, work)
call pzlatrz(m, n, l, a, ia, ja, desca, tau, work)
Description
The p?latrz routine reduces the m-by-n(m ≤ n) real/complex upper trapezoidal matrix sub(A) = [A(ia:ia+m-1, ja:ja+m-1) A(ia:ia+m-1, ja+n-l:ja+n-1)] to upper triangular form by means of orthogonal/unitary transformations.
The upper trapezoidal matrix sub(A) is factored as
sub(A) = ( R 0 )*Z,
where Z is an n-by-n orthogonal/unitary matrix and R is an m-by-m upper triangular matrix.
Input Parameters
- m
(global) INTEGER.
The number of rows to be operated on, that is, the number of rows of the distributed submatrix sub(A). m ≥ 0.
- n
(global) INTEGER.
The number of columns to be operated on, that is, the number of columns of the distributed submatrix sub(A). n ≥ 0.
- l
(global) INTEGER.
The number of columns of the distributed submatrix sub(A) containing the meaningful part of the Householder reflectors. l > 0.
- a
(local)
REAL for pslatrz
DOUBLE PRECISION for pdlatrz
COMPLEX for pclatrz
COMPLEX*16 for pzlatrz.
Pointer into the local memory to an array of DIMENSION(lld_a, LOCc(ja+n-1)). On entry, the local pieces of the m-by-n distributed matrix sub(A), which is to be factored.
- ia
(global) INTEGER.
The row index in the global array A indicating the first row of sub(A).
- ja
(global) INTEGER.
The column index in the global array A indicating the first column of sub(A).
- desca
(global and local) INTEGER array of DIMENSION (dlen_).
The array descriptor for the distributed matrix A.
- work
(local)
REAL for pslatrz
DOUBLE PRECISION for pdlatrz
COMPLEX for pclatrz
COMPLEX*16 for pzlatrz.
Workspace array, DIMENSION (lwork).
lwork ≥ nq0 + max(1, mp0), where
iroff = mod(ia-1, mb_a),
icoff = mod(ja-1, nb_a),
iarow = indxg2p(ia, mb_a, myrow, rsrc_a, nprow),
iacol = indxg2p(ja, nb_a, mycol, csrc_a, npcol),
mp0 = numroc(m+iroff, mb_a, myrow, iarow, nprow),
nq0 = numroc(n+icoff, nb_a, mycol, iacol, npcol),
numroc, indxg2p, and numroc are ScaLAPACK tool functions; myrow, mycol, nprow, and npcol can be determined by calling the subroutine blacs_gridinfo.
Output Parameters
- a
On exit, the leading m-by-m upper triangular part of sub(A) contains the upper triangular matrix R, and elements n-l+1 to n of the first m rows of sub(A), with the array tau, represent the orthogonal/unitary matrix Z as a product of m elementary reflectors.
- tau
(local)
REAL for pslatrz
DOUBLE PRECISION for pdlatrz
COMPLEX for pclatrz
COMPLEX*16 for pzlatrz.
Array, DIMENSION(LOCr(ja+m-1)). This array contains the scalar factors of the elementary reflectors. tau is tied to the distributed matrix A.
Application Notes
The factorization is obtained by Householder's method. The k-th transformation matrix, Z(k), which is used (or, in case of complex routines, whose conjugate transpose is used) to introduce zeros into the (m - k + 1)-th row of sub(A), is given in the form
![]()
where
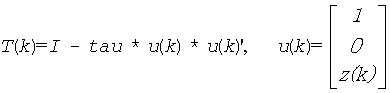
tau is a scalar and z( k ) is an (n-m)-element vector. tau and z( k ) are chosen to annihilate the elements of the k-th row of sub(A). The scalar tau is returned in the k-th element of tau and the vector u( k ) in the k-th row of sub(A), such that the elements of z(k ) are in a( k, m + 1 ), ..., a( k, n ). The elements of R are returned in the upper triangular part of sub(A).
Z is given by Z = Z(1)Z(2)...Z(m).