This section introduces Intel® Integrated Performance Primitives (Intel® IPP) functions for prime number generation.
The full list of prime number generation functions is given in Table “Intel IPP Prime Number Generation Functions”.
| Function Base Name | Operation |
|---|---|
| PrimeGetSize | |
| Gets the size of the IppsPrimeState context. | |
| PrimeInit | Initializes user-supplied memory as the IppsPrimeState context for future use. |
| PrimeGen | Generates a random probable prime number of the specified bitlength. |
| PrimeTest | Tests the given integer for being a probable prime. |
| PrimeSet | Sets the Big Number for primality testing. |
| PrimeSet_BN | Sets the Big Number for primality testing. |
| PrimeGet | Extracts the probable prime unsigned integer big number. |
| PrimeGet_BN | Extracts the probable prime positive Big Number. |
This section describes Intel IPP functions for generating probable prime numbers of variable lengths and validating probable prime numbers through a probabilistic primality test scheme for cryptographic use. A probable prime number is thus defined as an integer that passes the Miller-Rabin probabilistic primality-based test.
The scheme adopted for the probable prime number generation is
based on a well-known prime number theorem. Study shows that the
number of primitives that are no greater than the given large integer
x is closely approximated by the expression.
Let π(x) denote the number of primes that are not greater than x. In
this case the statement is true 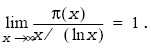
Further study indicates that if X represents
the event where the tested k-bit integer n is composite
and if Yt denotes
the event where the Miller-Rabin test with the security parameter
t declares n to be a prime,
the test error probability is upper bounded by
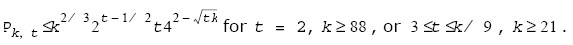
Subsequently, a practical strategy for generating a random k-bit probable prime is to repeatedly pick k-bit random odd integers until finding one integer that can pass a recognized probabilistic primality test scheme as a probable prime. The available set of probable prime number generation functions enables you to specify an appropriate value of the security parameter t used in the Miller-Rabin primality test to meet the cryptographic requirements for your application.
All Intel IPP for prime number generation use the context IppsPrimeState as an operational vehicle that carries the bitlength of the target probable prime number, the structure capturing the state of the pseudorandom number generation, the structuralized working buffer used for Montgomery modular computation in the Miller-Rabin primality test, and the buffer to store the generated probable prime number.
The following sequence of operations is required to generate a probable prime number of the specified bitlength:
- Call the function PrimeGetSize to get the size required to configure the IppsPrimeState context.
- Allocate memory through the operating system memory allocation function and configure the IppsPrimeState context by calling the function PrimeInit.
- Generate probable prime number of the specified bitlength by calling the function PrimeGen. If the returned IppStatus is ippStsInsufficientEntropy, then change the parameters of the pseudorandom generator and call the function PrimeGen again.
- Extract the generated probable prime number by calling the functions PrimeGet and PrimeGet_BN.
- Free the memory allocated to the IppsPrimeState context by calling the operating system memory-free service function.