This section describes Montgomery reduction scheme functions. The full list of these functions is given in Table “Intel IPP Montgomery Reduction Scheme Functions”.
| Function Base Name | Operation |
|---|---|
| MontGetSize | Gets the size of the IppsMontState context. |
| MontInit | Initializes the context and partitions the specified buffer space. |
| MontSet | Sets the input integer big number to a value and computes the Montgomery reduction index. |
| MontGet | Extracts the big number modulus. |
| MontForm | Converts input positive integer big number into Montgomery form. |
| MontMul | Computes Montgomery modular multiplication for positive integer big numbers of Montgomery form. |
| MontExp | Computes Montgomery exponentiation. |
Montgomery reduction is a technique for efficient implementation of modular multiplication without explicitly carrying out the classical modular reduction step.
This section describes functions for Montgomery modular reduction, Montgomery modular multiplication, and Montgomery modular exponentiation.
Let n be a positive integer, and let R and T be integers such that R > n, gcd (n, R)= 1, and 0 < T < nR. The Montgomery reduction of T modulo n with respect to R is defined as TR - 1 mod n.
For better results, functions included in the cryptography package use R = bk where b = 232 and k is the Montgomery index integer computed by the ceiling function of the bit length of the integer n over 32.
All functions use employ the context IppsMontState to serve as an operational vehicle to carry the Montgomery reduction index k, the integer big number modulus n, the least significant word n 0 of the multiplicative inverse of the modulus n with respect to the Montgomery reduction factor R, and a sufficient working buffer reserved for various Montgomery modular operations.
Furthermore, two new terms are introduced in this section:
- length of the context IppsMontState is defined as the data length of the modulus n carried by the structure
- size of the context IppsMontState is therefore defined as the maximum data length of such an integer modulus n that could be carried by this operational vehicle.
The following example can briefly illustrate the procedure of using the primitives described in this section to compute a classical modular exponentiation T = xe mod n. Consider computing T = x4 mod n, for some integer x with 0 < x < n.
First get the buffer size required to configure the context IppsMontState by calling MontGetSize and then allocate the working buffer using OS service function, with allocated buffer to call MontInit to initialize the context IppsMontState.
Set the modulus
n by
calling
MontSet and then convert
x into its
respective Montgomery form by calling
MontForm, that is,
computing
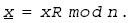
Then compute the Montgomery reduction of
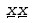
using the function
MontMul to generate
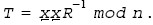
The Montgomery reduction of
T*
T
mod n with
respect to
R is
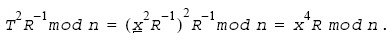
Further applying MontMul with this value and the value of 1 yields the desired result T = x 4 mod n.
The classical modular exponentiation should be computed by performing the following sequence of operations:
- Get the buffer size required to configure the context IppsMontState by calling the function MontGetSize. For limited memory system, choose binary method, and otherwise, choose sliding window method. Using the binary method reduces the buffer size significantly while using sliding window method enhances the performance.
- Allocate working buffer through an operating system memory allocation function and configure the structure IppsMontState by calling the function MontInit with the allocated buffer and the choice made on the modular exponential method at time invoking MontGetSize.
- Call the function MontSet to set the integer big number module for IppsMontState.
- Call the function MontForm to convert the integer x to be its Montgomery form.
- Call the function MontExp to compute the Montgomery modular exponentiation.
- Call the function MontMul to compute the Montgomery modular multiplication of the above result with the integer 1 as to convert the above result back to the desired classical modular exponential result.
- Free the memory using an operating system memory free function, if needed.