Ασκησεις 22.1 και 22.2

1.

Αποδειξετε αλγεβρικά οτι ο αντιστροφος μετασχηματισμος Lorentz δινεται απο τον αρχικο αντικαθιστωντας $\vec{v}\rightarrow -\vec{v}$. Δηλαδή αν δυο συστηματα αναφοράς συνδεονται με τον μετασχηματισμό

$$\gamma(x-v t)$$ x' =

y' = y

z' = z

$$\gamma(t-\frac{v}{c^2}x)$$ t' =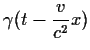

τοτε ο αντιστροφος μετασχηματισμος θα ειναι

$$\gamma(x'+v t')$$ x =

y = y'

z = z'

$$\gamma(t'+\frac{v}{c^2}x')$$ t =

2.

Αποδειξετε οτι η ποσοτητα

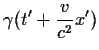(x)²+(y)²+(z)²-(ct)² = (x')²+(y')²+(z')²-(ct')²

μενει αναλλοιωτη κατω απο μετασχηματισμους Lorentz. Συμπερανατε απο αυτο πως ενα σφαιρικο κυμα φωτος στο κενο παραμενει σφαιρικο και διαδιδεται με την ιδια ταχυτητα και στα δυο συστηματα αναφορας.